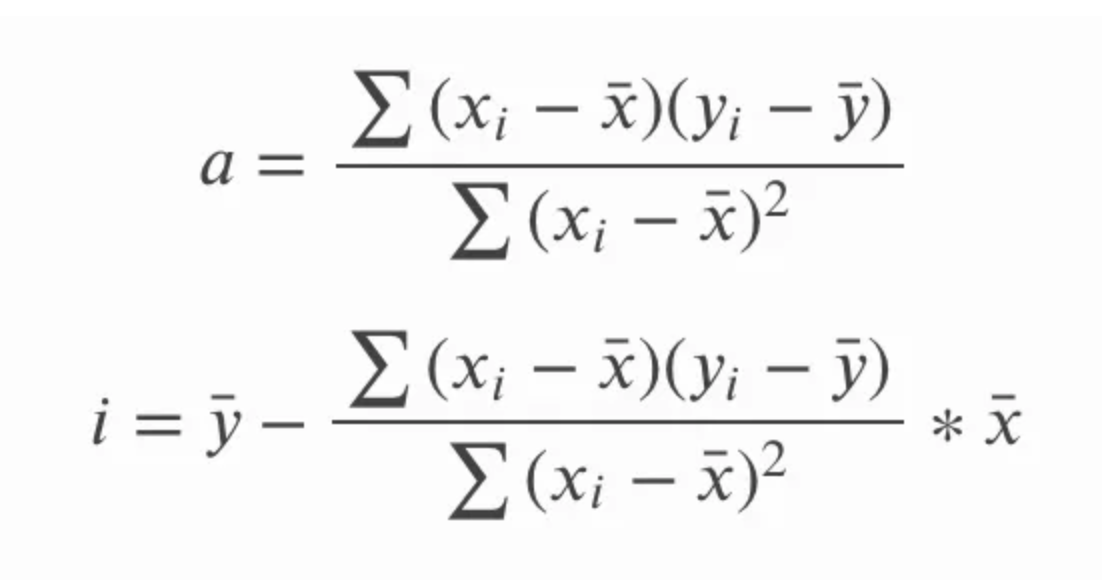Einfache lineare Regression: Alles, was du wissen musst

Jede Geschichte beginnt irgendwo, und für den Datenanalysten oder Datenwissenschaftler ist der Anfang der Geschichte oft eine einfache lineare Regression. Die einfache lineare Regression ist vielleicht sogar das grundlegendste Modell von allen. Wenn du also ernsthaft Datenanalyst/in oder Datenwissenschaftler/in werden willst, ist die einfache lineare Regression (und Regressionen im Allgemeinen) ein absolutes Muss.

Das Erlernen der Regression lohnt sich nicht nur, weil sie eine unschätzbare Technik zur Beantwortung drängender Fragen in praktisch jedem Bereich ist, sondern sie öffnet auch die Tür zu einem tieferen Verständnis einer Vielzahl anderer Dinge, wie Hypothesentests, Kausalschlüsse und Vorhersagen. Dann besuche noch heute unseren Kurs Einführung in die Regression in R und unseren Kurs Einführung in die Regression mit statsmodels in Python.

Was ist eine einfache lineare Regression? 

Die einfache lineare Regression ist eine lineare Regression mit einer unabhängigen Variable, auch erklärende Variable genannt, und einer abhängigen Variable, auch Antwortvariable genannt. Bei der einfachen linearen Regression ist die abhängige Variable kontinuierlich. 

Gewöhnlicher Kleinstquadrat-Schätzer 

Die gebräuchlichste Art, eine einfache lineare Regression durchzuführen, ist die Schätzung nach der Methode der gewöhnlichen kleinsten Quadrate (OLS). Da OLS die bei weitem gängigste Methode ist, wird der Teil "gewöhnliche kleinste Quadrate" oft impliziert, wenn wir von einfacher linearer Regression sprechen.

Bei der gewöhnlichen kleinsten Quadratzahl wird die Summe der quadrierten Differenzen zwischen den beobachteten Werten (den tatsächlichen Datenpunkten) und den aus der Regressionsgeraden vorhergesagten Werten minimiert. Diese Differenzen werden als Residuen bezeichnet, und die Quadrierung stellt sicher, dass sowohl positive als auch negative Residuen gleich behandelt werden. 

Wie die einfache lineare Regression verwendet wird

Die einfache lineare Regression hilft dabei , Vorhersagen zu treffen und Beziehungen zwischen einer unabhängigen und einer abhängigen Variablezu verstehen. Du möchtest zum Beispiel wissen, wie sich die Höhe eines Baumes (unabhängige Variable) auf die Anzahl der Blätter auswirkt, die er hat (abhängige Variable). Wenn du Daten sammelst und ein einfaches lineares Regressionsmodell anpasst, kannst du die Anzahl der Blätter anhand der Höhe des Baumes vorhersagen. Das ist der Teil "Vorhersagen treffen". Dieser Ansatz zeigt aber auch, wie sehr sich die Anzahl der Blätter im Durchschnitt verändert, wenn der Baum größer wird. So wird auch die einfache lineare Regression genutzt, um Zusammenhänge zu verstehen.  

Einfache lineare Regressionsgleichung

Werfen wir einen Blick auf die einfache lineare Regressionsgleichung. Wir können damit beginnen, die Form des Steigungsabschnitts einer Geraden zu betrachten, indem wir die Notation verwenden, die in Geometrie- oder Algebra-Lehrbüchern üblich ist. Das heißt, wir fangen ganz am Anfang an.

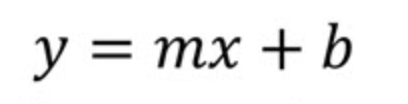
Hier

• m ist die Steigung der Linie
• b ist der Schnittpunkt

Im Kontext der Datenwissenschaft siehst du stattdessen eher diese Gleichung: 

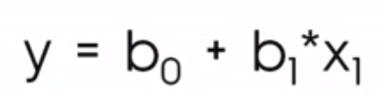
Wo

• b0 ist der y-Achsenabschnitt 
• b1 ist die Steigung

Die Notation mit b0 und b1 hilft uns zu verstehen, dass es sich um eine Situation handelt, in der wir eine Vorhersage über yund deshalb nennen wir sie ŷDeshalb nennen wir es oder y-hat, denn wir erwarten nicht, dass unsere Regressionsgerade tatsächlich durch alle Punkte geht.

Die folgende Visualisierung zeigt den konzeptionellen Unterschied zwischen der Form des Steigungsabschnitts der Geraden (links) und der Regressionsgleichung (rechts). In der Sprache der linearen Algebra würden wir sagen, dass das lineare Gleichungssystem überdeterminiert ist, d.h. es gibt mehr Gleichungen (etwa dreißig) als Unbekannte (zwei), so dass wir nicht erwarten, eine Lösung zu finden.

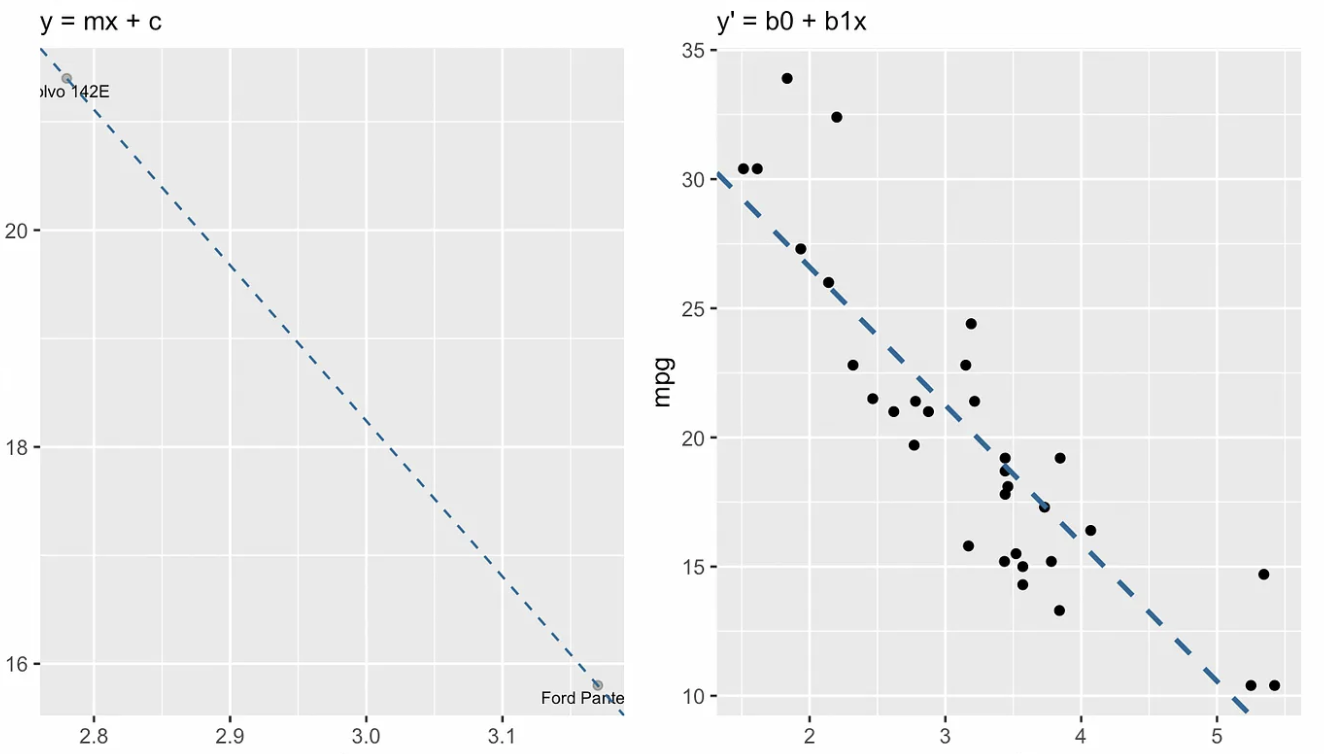Slope-Intercept-Form vs. einfache lineare Regressionsgleichung. Bild vom Autor

Koeffizienten des einfachen linearen Regressionsmodells

Wenn wir nur die Steigungs-Absatz-Gleichung verwenden würden, würden wir die Werte von m (Steigung) und b (y-Absatz) ermitteln , indem wir zuerst die Steigung als "Anstieg über dem Verlauf" berechnen, d. h. die Änderung von y gegenüber der Änderung von x zwischen zwei Punkten auf der Linie messen . Wenn wir die Steigung gefunden haben, können wir den y-Achsenabschnitt b bestimmen, indem wir die Koordinaten eines Punktes auf der Geraden in die Gleichung einsetzen und nach b auflösen . In diesem letzten Schritt erhältst du den Punkt, an dem die Linie die y-Achse schneidet.

Das funktioniert bei der Regression nicht, weil es keine Linie gibt, die durch alle Punkte geht. Deshalb suchen wir stattdessen die Linie der besten Anpassung. Zum Glück gibt es einfache, geschlossene Gleichungen, um Steigung und Achsenabschnitt zu bestimmen. 

Die Steigung kann durch Multiplikation der Korrelation berechnet werden r mit dem Quotienten aus der Standardabweichung von y über die Standardabweichung von x. Das macht intuitiv Sinn, weil wir den Korrelationskoeffizienten im Wesentlichen in Einheiten der ursprünglichen Variablen umrechnen. In der folgenden Gleichung bezieht sich a auf die Steigung und sy und sx auf die Standardabweichung von y bzw. die Standardabweichung von x.

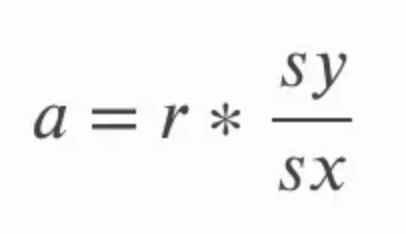
Der Achsenabschnitt der Anpassungsgeraden für die einfache lineare Regression kann berechnet werden, nachdem wir die Steigung berechnet haben. Dazu subtrahieren wir das Produkt aus der Steigung und dem Mittelwert von x vom Mittelwert von y. In der folgenden Gleichung, i auf den y-Achsenabschnitt und die Gerade über die x und y ist eine Art, sich auf den Mittelwert von x und y zu bezeichnen; wir bezeichnen diese Begriffe als x-bar und y-bar.

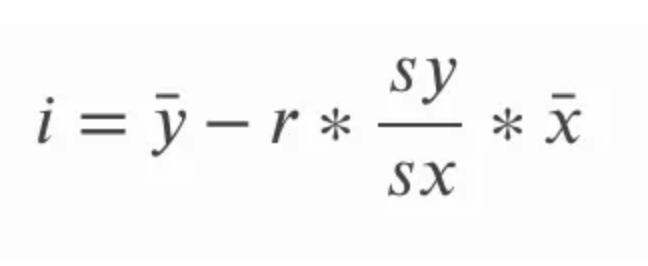
Um gründlich zu sein, können wir auch andere Möglichkeiten finden, diese Gleichungen zu schreiben. Erinnere dich daran, dass die Standardabweichung dasselbe ist wie die Quadratwurzel aus der Varianz. Anstatt sich also auf die Standardabweichung von y und die Standardabweichung von x zu beziehen, könnten wir uns auch auf die Quadratwurzel aus der Varianz von y und die Quadratwurzel aus der Varianz von x beziehen . Die Varianz selbst ist, wie wir uns erinnern, der Durchschnitt der Summe der Quadrate. 

In der obigen Gleichung für die Steigung a könnten wir auch sy und sx in Form der Standardabweichung schreiben , und wir könnten auch die längere Form der Gleichung für die Korrelation r aufstellen . Dann können wir die Gleichung kreuzmultiplizieren und vereinfachen, indem wir gemeinsame Terme entfernen, und erhalten die folgenden Gleichungen für Steigung und Achsenabschnitt. Hier geht es weniger darum, zu zeigen, wie die eine Gleichung in die andere übergeht, sondern vielmehr darum zu betonen, dass beide Gleichungen gleich sind, da du die eine oder die andere sehen kannst. 

Eine weitere interessante Folge ist, dass die einfache lineare Regressionsgerade durch den zentralen Punkt geht, der der Mittelwert von x und der Mittelwert von yist . Mit anderen Worten: Die einfache lineare Regression schneidet sich im Durchschnitt der unabhängigen und abhängigen Variablen, unabhängig von der Verteilung der Datenpunkte, was der einfachen linearen Regression eine Art "ausgleichende" Eigenschaft verleiht.

Weitere Möglichkeiten zur Ermittlung der Koeffizienten des einfachen linearen Regressionsmodells 

Wir haben gesehen, wie man die Koeffizienten eines einfachen linearen Regressionsmodells mit Hilfe von einfachen Gleichungen ermitteln kann. Hier werden wir uns einige andere Methoden, die lineare Algebra und Infinitesimalrechnung beinhalten, genauer ansehen. Vor allem in Programmierumgebungen werden fortschrittlichere Techniken eingesetzt, weil diese schneller und präziser sind (die Sache mit dem Quadrieren, um die Varianz zu finden, kann die Präzision verringern).

• Lineare Algebra: Es gibt einige Techniken aus der linearen Algebra, um die Koeffizienten einer einfachen linearen Regression zu finden. Wir können die Koeffizienten in einem einfachen linearen Regressionsmodell ermitteln, indem wir die so genannte Normalgleichung lösen. Die Normalgleichung ist interessant, aber bei großen Datensätzen nicht empfehlenswert, weil sie eine Matrixinversion beinhaltet, die teuer sein kann. Eine andere Methode der linearen Algebra ist die QR-Zerlegung, die ohne Matrixinversion auskommt und bekanntermaßen numerisch stabil ist.
• Calculus: Wir können die Steigung und den Achsenabschnitt eines einfachen linearen Regressionsmodells ermitteln, indem wir die partiellen Ableitungen der Summe der quadrierten Fehler (SSE) in Bezug auf die Steigung und den Achsenabschnitt nehmen und sie gleich Null setzen, um die Koeffizienten zu bestimmen. Das ist eine Möglichkeit. Eine weitere Option, die mit der Infinitesimalrechnung zusammenhängt, ist der Gradientenabstieg, ein iteratives Optimierungsverfahren, das zur Minimierung der SSE und zur Ermittlung von Steigung und Achsenabschnitt eingesetzt werden kann. Der Gradientenabstieg ist eng mit der Infinitesimalrechnung verbunden, da er auf dem Gradienten basiert, der der Vektor der partiellen Ableitungen ist.

Annahmen des einfachen linearen Regressionsmodells

Werfen wir nun einen Blick auf die wichtigsten Annahmen des einfachen linearen Regressionsmodells. Wenn diese Annahmen verletzt werden, sollten wir vielleicht einen anderen Ansatz in Betracht ziehen. Vor allem die ersten drei sind starke Annahmen und sollten nicht ignoriert werden.

1. Linearität: Die Beziehung zwischen den unabhängigen und abhängigen Variablen muss linear sein. Wenn die Beziehung nicht linear ist, wird das Modell sie nicht gut abbilden.
2. Unabhängigkeit von Fehlern: Die Residuen sollten unabhängig voneinander sein. Das bedeutet, dass es keine Muster oder Korrelationen zwischen den Residuen geben sollte. Darauf solltest du bei zeitlich geordneten Daten genau achten.
3. Homoskedastizität: Die Residuen sollten eine konstante Varianz über alle Werte der unabhängigen Variable haben. Wenn sich die Varianz ändert (Heteroskedastizität), können die Vorhersagen in bestimmten Bereichen von x ungenauer werden.
4. Normalität der Residuen: Die Residuen sollten idealerweise einer Normal- oder Gaußverteilung folgen. Das ist wichtig für statistische Tests und um das Vertrauen in unsere Schätzung zu stärken. Für Vorhersagen ist das weniger wichtig. 

Bewertung des einfachen linearen Regressionsmodells

Nehmen wir an, wir haben ein einfaches lineares Regressionsmodell erstellt. Woher wissen wir, ob es gut passt? Um diese Frage zu beantworten, können wir uns Diagnoseplots und Modellstatistiken ansehen. 

Einfache lineare Regressionsdiagramme

Diagnosegrafiken helfen uns zu sehen, ob ein einfaches lineares Regressionsmodell gut passt und nicht gegen unsere Annahmen verstößt. Alle Muster oder Abweichungen in diesen Diagrammen deuten auf Modellprobleme hin, die beachtet werden müssen, oder auf Informationen, die nicht erfasst wurden. Eine diagnostische Darstellung, die es nur bei der einfachen linearen Regression gibt, ist die Darstellung der x-Werte gegen die Residuen, wie du unten siehst. Weitere Diagramme sind das Q-Q-Diagramm, das Diagramm für die Skalenposition, die Anzahl der Beobachtungen im Vergleich zur Entfernung des Kochs und andere. 

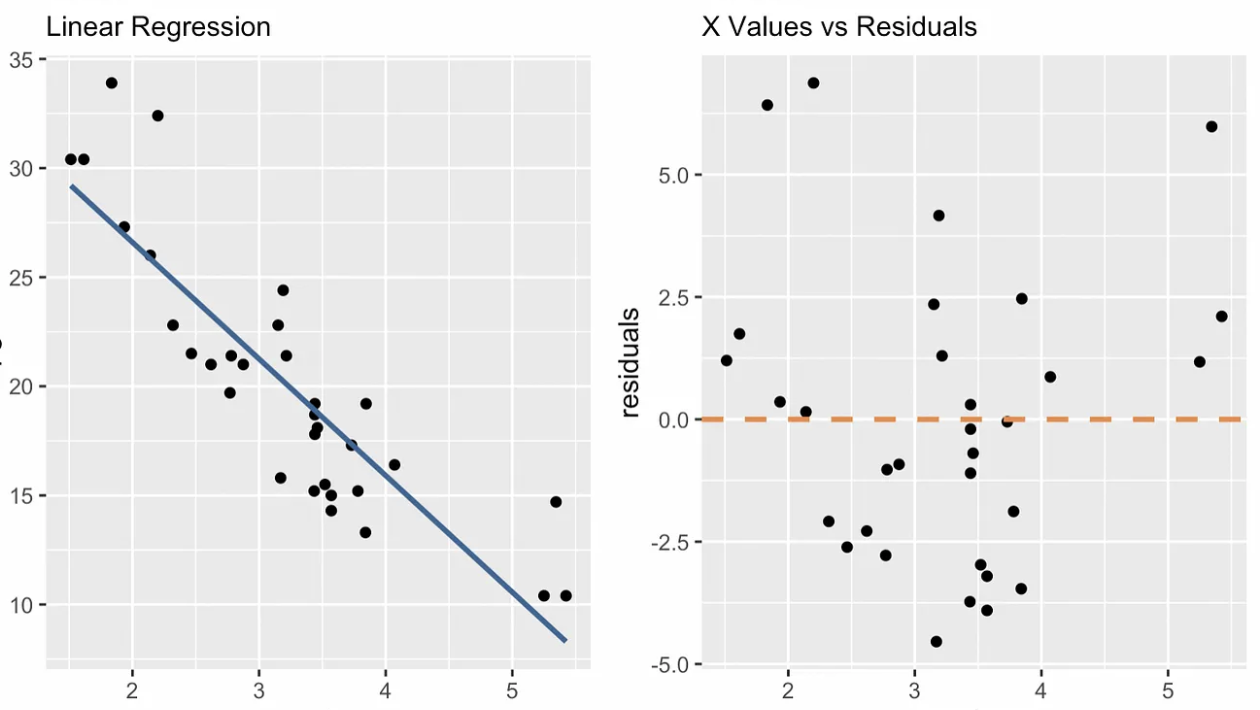x-Werte vs. Residuen Diagnoseplot. Bild vom Autor

Statistik des einfachen linearen Regressionsmodells

Modellstatistiken wie R-Quadrat und bereinigtes R-Quadrat geben an, wie gut die unabhängige Variable die Varianz der abhängigen Variable erklärt. Die F-Statistik testet die Gesamtsignifikanz des Modells, und die p-Werte für die Koeffizienten geben Aufschluss über die Auswirkungen der einzelnen Prädiktoren. 

Wie man ein einfaches lineares Regressionsmodell interpretiert

Bei der Interpretation der Ergebnisse einer einfachen linearen Regression sollten wir darauf achten, dass wir die Beziehung zwischen der unabhängigen Variable und der abhängigen Variable genau beschreiben.

So interpretierst du die Steigung und den Achsenabschnitt

Wir sollten vor allem darauf achten, wie wir über die beiden Schlüsselkomponenten sprechen: die Steigung und den Achsenabschnitt.

• Der Achsenabschnitt sagt dir, wo die Regressionslinie die y-Achse schneidet. In der Praxis stellt sie den Wert der abhängigen Variable dar, wenn die unabhängige Variable Null ist. Es ist wichtig zu wissen, dass der Intercept nicht immer interpretierbar ist. In unserem früheren Beispiel mit Bäumen hätte unser Modell eine bestimmte Anzahl von Blättern für Bäume mit einer Höhe von Null vorausgesagt. Es hätte keinen Sinn gemacht, den Schnittpunkt in diesem Zusammenhang zu interpretieren. 
• Die Steigung gibt an, um wie viel sich die abhängige Variable bei einem Anstieg der unabhängigen Variable um eine Einheit verändern wird. Eine positive Steigung deutet auf eine positive Beziehung hin, bei der die abhängige Variable steigt, wenn die unabhängige Variable steigt. Eine negative Steigung bedeutet das Gegenteil.

Ein wichtiger Punkt ist, dass Korrelation nicht gleichbedeutend mit Kausalität ist. Analysten, die mit diesem Konzept vertraut sind, können sich bei der Interpretation einer einfachen linearen Regression trotzdem vertun, weil sie nicht geübt sind, die richtigen Worte zu verwenden. Du würdest nicht sagen, dass die Höhe eines Baumes zu mehr Blättern führt, sondern du könntest sagen, dass eine Zunahme der Baumhöhe um eine Einheit mit einer Zunahme einer bestimmten Anzahl von Blättern verbunden ist. 

Eine weitere wichtige Überlegung ist, dass eine Extrapolation über den Bereich der Daten hinaus möglicherweise keine zuverlässigen Vorhersagen liefert. Ein einfaches lineares Regressionsmodell, das die Anzahl der Blätter aus der Höhe des Baumes vorhersagt, könnte bei sehr kurzen oder sehr hohen Bäumen nicht sehr genau sein, vor allem wenn kurze oder hohe Bäume bei der Erstellung unseres Modells nicht berücksichtigt wurden. 

Wie man über Transformationen nachdenkt

Lineare Modelle werden so genannt, weil sie in ihrer Funktionsform linear sind. Bei der einfachen linearen Regression wird die Beziehung zwischen der Reaktionsvariablen y und der Prädiktorvariablen x als lineare Kombination aus dem Prädiktor und einer Konstante modelliert. Trotzdem wirst du vielleicht überrascht sein, was du mit einer einfachen linearen Regression alles machen kannst. Das Modell geht von einer geradlinigen Beziehung zwischen den Variablen aus, aber du kannst Transformationen einführen, um nicht-lineare Beziehungen zu erfassen.

Betrachte zum Beispiel die nicht-lineare Beziehung, die das Wachstum der Vorfahren nach Generationen darstellt, wobei die Anzahl der Vorfahren mit jeder Generation exponentiell zu wachsen scheint: zwei Eltern, vier Großeltern, acht Urgroßeltern und so weiter. Du würdest nicht erwarten, dass ein lineares Modell exponentielles Wachstum erfasst, aber indem du log(y) anstelle von y vorhersagst, linearisierst du die Beziehung .

Wenn du jedoch weiterdenkst, wird dir klar, dass es kein exponentielles Wachstum der Vorfahren gibt, weil sich die Wachstumsrate im Laufe der Zeit dramatisch verlangsamt, weil entfernte Vorfahren an mehreren Stellen im Stammbaum auftauchen. Aus diesem Grund könnte die Verwendung von log(y) unser Modell übermäßig verstärkt haben. Um dies abzumildern, können wir eine neue Variable erstellen, die eine Quadratwurzeltransformation von x ist, und diese stattdessen als Prädiktor verwenden. Ichbehaupte nicht, dass irgendeines dieser Modelle richtig ist, und ich versuche auch nicht, es vollständig zu interpretieren, aber ich versuche zu zeigen, dass log(y) und die Quadratwurzel aus x nichtlineare Transformationen sind, die in Bezug auf die Koeffizienten linear in die Gleichung eingehen, sodass wir immer noch eine einfache lineare Regression haben.

Einfache lineare Regression in R und Python

Betrachten wir eine einfache lineare Regression in R und Python.

R-Programmierung

R ist eine gute Option für eine einfache lineare Regression.

Manuelle Berechnung von Steigung und Achsenabschnitt

Wir können die Koeffizienten selbst ermitteln, indem wir den Mittelwert und die Standardabweichung unserer Variablen berechnen. 

# Manually calculate the slope and intercept in R

# Sample data
X <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 5, 4, 5)

# Calculate means
mean_X <- mean(X)
mean_y <- mean(y)

# Calculate standard deviations
sd_X <- sd(X)
sd_y <- sd(y)

# Calculate correlation
correlation <- cor(X, y)

# Calculate slope (b1) using the formula: b1 = (correlation * sd_y) / sd_X
slope <- (correlation * sd_y) / sd_X

# Calculate intercept (b0) using the formula: b0 = mean_y - slope * mean_X
intercept <- mean_y - slope * mean_X

# Print the slope and intercept
cat("Slope (b1):", slope, "\n")
cat("Intercept (b0):", intercept, "\n")

# Use the manually calculated coefficients to predict y values
y_pred <- intercept + slope * X
cat("Predicted values:", y_pred, "\n")

Verwendung der Funktion lm()

In R können wir eine Regression mit der Funktion lm() erstellen, auf die wir zugreifen können, ohne irgendwelche Bibliotheken verwenden zu müssen. 

# Fit the model 
model <- lm(y ~ X) 

# Print the summary of the regression 
summary(model)

Python

Python ist eine weitere gute Option für einfache lineare Regressionen. 

Manuelle Berechnung von Steigung und Achsenabschnitt

Hier finden wir den Mittelwert und die Standardabweichung für jede Variable. 

import numpy as np

# Sample data
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Calculate means
mean_X = np.mean(X)
mean_y = np.mean(y)

# Calculate standard deviations
sd_X = np.std(X, ddof=1)
sd_y = np.std(y, ddof=1)

# Calculate correlation
correlation = np.corrcoef(X, y)[0, 1]

# Calculate slope (b1) using the formula: b1 = (correlation * sd_y) / sd_X
slope = (correlation * sd_y) / sd_X

# Calculate intercept (b0) using the formula: b0 = mean_y - slope * mean_X
intercept = mean_y - slope * mean_X

# Print the slope and intercept
print(f"Slope (b1): {slope}")
print(f"Intercept (b0): {intercept}")

# Use the manually calculated coefficients to predict y values
y_pred = intercept + slope * X

print(f"Predicted values: {y_pred}")

Verwendung von Statistikmodellen

statsmodels ist eine Möglichkeit für eine einfache lineare Regression.

import statsmodels.api as sm

# Adding a constant for the intercept
X = sm.add_constant(X)

# Fit the model
model = sm.OLS(y, X)
results = model.fit()

# Print the summary of the regression
print(results.summary())

Einfache lineare Regression, t-Test und ANOVA

Die einfache lineare Regression wird bei Hypothesentests verwendet und spielt eine zentrale Rolle bei t-Tests und der Varianzanalyse (ANOVA). 

Einfache lineare Regression und t-Test

Ein t-Test wird oft verwendet, um festzustellen, ob sich die Steigung der Regressionslinie signifikant von Null unterscheidet. Dieser Test hilft uns zu verstehen, ob die unabhängige Variable einen statistisch signifikanten Effekt hat. Grundsätzlich formulieren wir eine Nullhypothese, die besagt, dass die Steigung der Regressionsgeraden gleich Null ist, was bedeutet, dass es keine lineare Beziehung gibt, und der t-Test bewertet dies. Die einfache lineare Regression ist hier von Bedeutung, denn eine einfache lineare Regression mit einer binären unabhängigen Variable ist dasselbe wie ein Mittelwertunterschied, wie wir ihn bei einem t-Test sehen.

Einfache lineare Regression und ANOVA

Die Varianzanalyse (ANOVA) ist ein statistisches Verfahren, mit dem die Gesamtanpassung des Modells bewertet und festgestellt werden kann, ob die unabhängige Variable einen erheblichen Teil der Varianz der abhängigen Variable erklärt. Wir teilen die Gesamtvarianz der abhängigen Variable in zwei Komponenten auf: die durch das Regressionsmodell erklärte Varianz (zwischen den Gruppen) und die Varianz aufgrund von Residuen oder Fehlern (innerhalb der Gruppen). Der F-Test in der ANOVA prüft im Wesentlichen, ob das Regressionsmodell als Ganzes besser zu den Daten passt als ein Modell ohne Prädiktoren. In unserem Beispiel mit der Baumhöhe und der Blattzahl würde die ANOVA helfen herauszufinden, ob die Einbeziehung der Baumhöhe unsere Fähigkeit, die Anzahl der Blätter vorherzusagen, signifikant verbessert.

Alternativen zu OLS Einfache lineare Regression 

Wir haben bereits gesagt, dass die gewöhnliche kleinste Quadrate der bei weitem gängigste Schätzer in der einfachen linearen Regression ist, und wir haben uns in diesem Artikel auf OLS konzentriert. Wir sollten jedoch bedenken, dass der gewöhnliche Kleinste-Quadrate-Schätzer empfindlich auf Ausreißer reagiert bzw. nicht robust gegenüber Ausreißern ist. Wenn du also einen sehr einflussreichen Datenpunkt hinzufügst, kann sich die Steigung und der Schnittpunkt der Linie dramatisch verändern.  

Aus diesem Grund gibt es nicht-parametrische Optionen. Die folgende Darstellung zeigt die gewöhnliche kleinste Quadratzahl mit drei nicht-parametrischen Alternativen: Median absolute Abweichung (MAD), kleinste mediane Quadrate (LMS) und Theil-Sen. Beachte, dass Steigung und Achsenabschnitt für jeden Schätzer unterschiedlich sind. Wenn wir einen sehr einflussreichen Punkt hinzufügen würden, z. B. bei den Koordinaten x = 7 und y = 70, dann würde sich die gewöhnliche Regressionsgerade der kleinsten Quadrate am stärksten verändern.

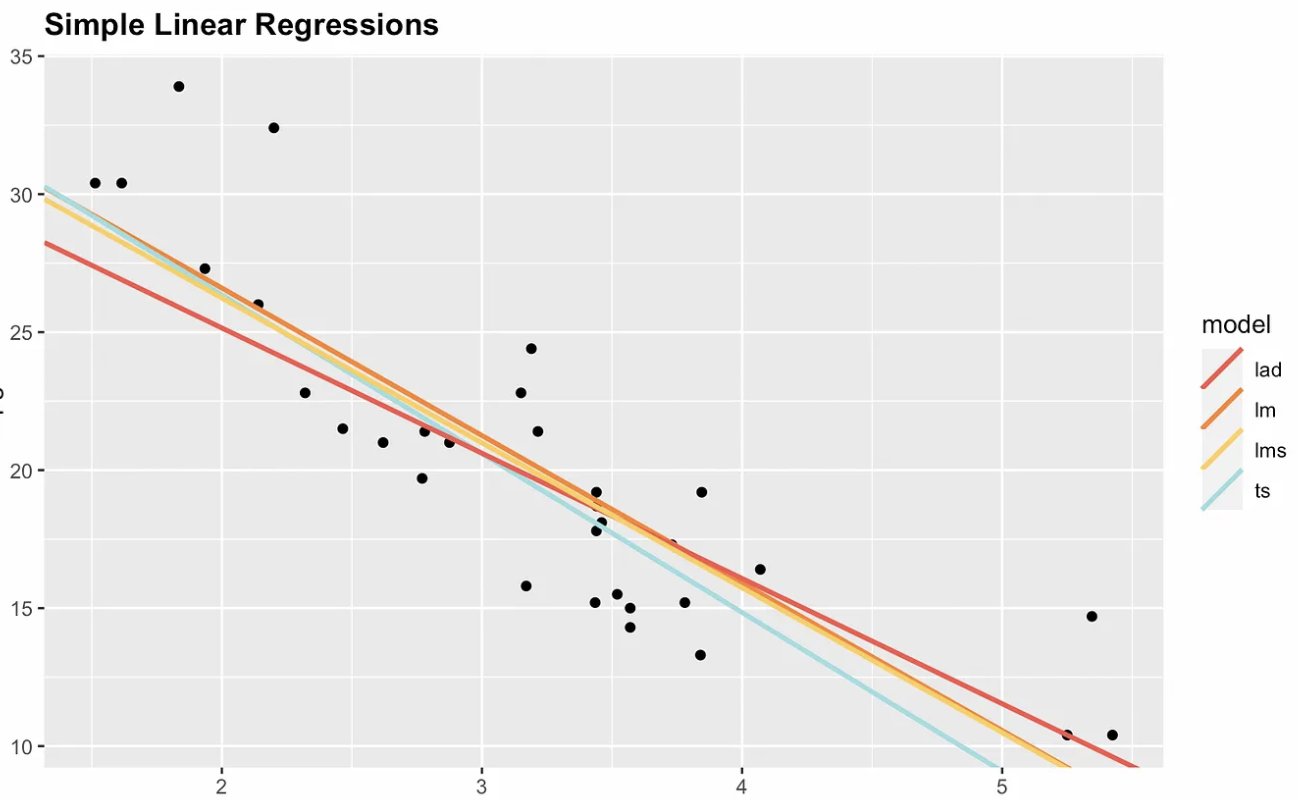Vier einfache lineare Regressionsoptionen. Bild vom Autor

Schlussgedanken

Die einfache lineare Regression ist der Ausgangspunkt für das Verständnis komplexerer Zusammenhänge in den Daten. Um dir dabei zu helfen, bietet DataCamp Tutorials an, mit denen du weiter üben kannst, z. B. unser Tutorial Grundlagen der linearen Regression in Python, das Tutorial Lineare Regression in R und das Lineare Regression in Excel: Ein umfassender Leitfaden für Einsteiger tutorial. Diese Ressourcen führen dich durch die Verwendung verschiedener Tools zur Durchführung linearer Regression und zum Verständnis ihrer Anwendungen. Wenn du deine Kenntnisse erweitern möchtest, solltest du dir unsere Multiple Linear Regression in R ansehen: Tutorial With Examples, das komplexere Modelle mit mehreren Prädiktoren behandelt.