Introduction à l'estimation du maximum de vraisemblance (EMV)

L'estimation des paramètres est une étape fondamentale dans l'analyse statistique et l'apprentissage automatique. Parmi les différentes méthodes disponibles,l'estimation du maximum de vraisemblance (EMV) est l'une des approches les plus utilisées en raison de sa nature intuitive, de sa rigueur mathématique et de sa large applicabilité à différents types de données et de modèles.

Dans cet article, vous apprendrez ce qu'est le MLE, vous explorerez ses fondements mathématiques à travers des dérivations détaillées et des exemples, et vous découvrirez des méthodes de calcul pratiques pour mettre en œuvre efficacement le MLE.

Qu'est-ce que l'estimation du maximum de vraisemblance (EMV) ?

L'estimation du maximum de vraisemblance (EMV) est une méthode statistique importante méthode statistique utilisée pour estimer les paramètres d'une distribution de probabilité en maximiser la fonction de vraisemblance.

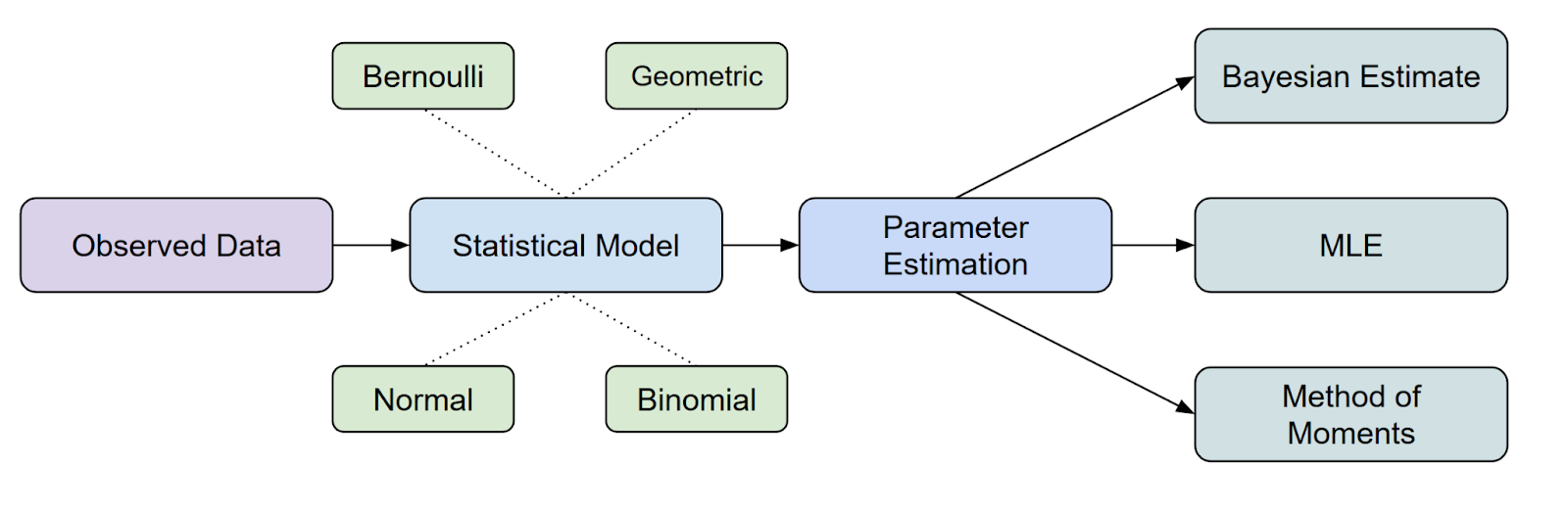
En ce qui concerne la place de la MLE dans l' l'inférence statistique, il s'agit de l'une des méthodes les plus courantes dont nous disposons pour estimer des paramètres.

Cependant, vous pourriez vous poser une autre question ici. Qu'est-ce qu'une fonction de vraisemblance ? Discutons-en plus en détail.

Qu'est-ce que la fonction de vraisemblance ?

Nous pouvons considérer la fonction de vraisemblance comme un moyen de mesurer dans quelle mesure un ensemble particulier de paramètres explique les données que vous avez observées.

En d'autres termes, cela répond à la question suivante : « Compte tenu de ces valeurs paramétriques, quelle est la probabilité que je constate ces données ? » Cependant, il existe une confusion courante entre la probabilité et la vraisemblance :

• La probabilité consiste à prédire des données. prédire des données à partir de paramètres.
• L' de vraisemblance mesure le degré de plausibilité de différentes valeurs de paramètres, compte tenu des données observées. Il s'agit d'une fonction de paramètres pour des données fixes. En revanche, la probabilité est une fonction des données pour des paramètres fixes.

En résumé, la fonction de vraisemblance utilise les paramètres de votre modèle comme données d'entrée et vous fournit un nombre qui représente la plausibilité de ces paramètres, compte tenu de vos données.

Plus la valeur de la fonction de vraisemblance est élevée, mieux ces paramètres expliquent vos données.

Pour simplifier davantage, la fonction de vraisemblance nous aide à « noter » différents choix de paramètres, afin que nous puissions sélectionner ceux qui rendent nos données observées les plus probables.

Maintenant que nous avons compris la différence entre probabilité et vraisemblance, ainsi que l'utilité du MLE, passons aux mathématiques sous-jacentes.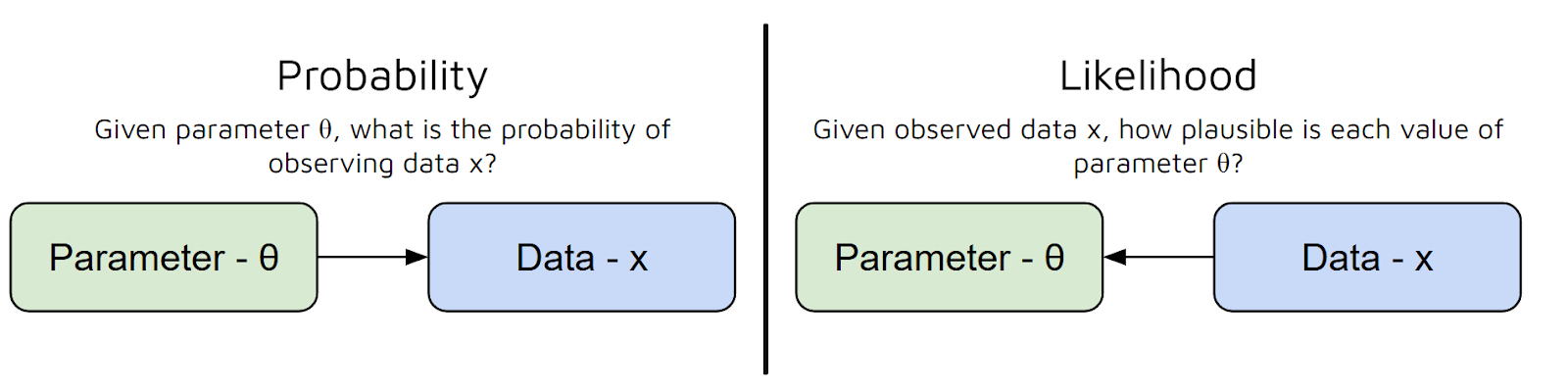

Comment dériver la formule MLE

Avant de passer à des exemples spécifiques, examinons comment l'estimateur du maximum de vraisemblance (EMV) est dérivé en général. Nous allons passer en revue chaque étape et expliquer le raisonnement qui la sous-tend.

Étape 1 : Définir le modèle de probabilité

Supposons que nous disposons d'un ensemble de données : x₁, x₂, ..., xₙ. Nous estimons que ces points de données sont générés à partir d'une distribution de probabilité qui dépend d'un paramètre inconnu θ (thêta). Notre objectif principal est d'estimer θ. 

Par exemple, si notre ensemble de données concernait des lancers de pièces, θ pourrait être la probabilité d'obtenir pile. Si l'ensemble de données était continu, comme la taille des élèves d'une classe, θ pourrait être la moyenne d'une distribution normale.

Étape 2 : Écrire la fonction de vraisemblance

La fonction de vraisemblance mesure la probabilité d'observer vos données pour différentes valeurs de θ. Il est défini comme suit :

Intuitivement, nous demandons, étant donné que le paramètre θ prend une valeur spécifique, quelle est la probabilité d'observer cet ensemble de données particulier ? 

Cet ensemble de données est représenté sous forme de probabilité conjointe d'observer les points de données individuels (x₁, x₂, ..., xₙ), en supposant qu'ils ont été générés selon le modèle paramétré par θ.

En utilisant la règle de la chaîne en probabilité, nous pouvons développer l'équation ci-dessus comme suit :

Cependant, cette équation est assez complexe. Nous partons donc du principe que les points de données sontindépendants de l' , ou plus précisément, conditionnellement indépendants.

Ce faisant, nous pouvons obtenir la probabilité conjointe comme étant le produit des probabilités individuelles :

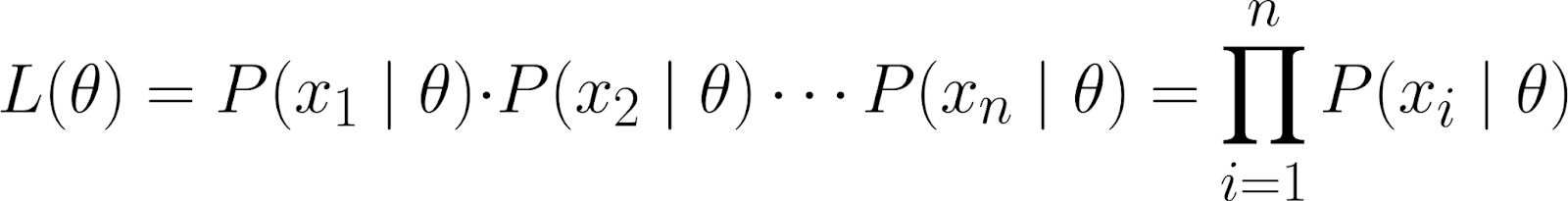
Étant donné que nos points de données observés sont conditionnellement indépendants de θ, nous savons que l'équation suivante est vraie :

En effet, nous avons supposé qu'une fois la valeur de θ connue, les points de données x₁ et x₂ sont conditionnellement indépendants.

Étape 3 : Déterminez la valeur de θ qui maximise la vraisemblance.

Nous sommes dans une situation où nous devons trouver les valeurs de θ qui maximisent la fonction de vraisemblance. maximisent la fonction de vraisemblance(c'est-à-dire qui rend les données observées les plus probables) :

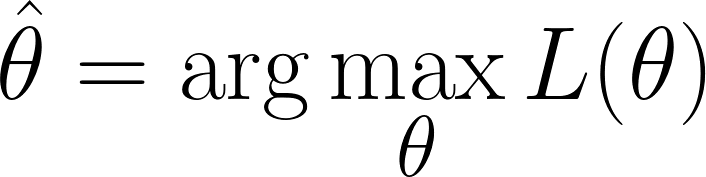
Cependant, rappelons que notre fonction de vraisemblance contient un produit. Travailler avec des produits peut s'avérer compliqué, en particulier lorsque de nombreux points de données sont impliqués. Pour simplifier, nous prenons lelogarithme d' e de la fonction de vraisemblance, car cela convertit le produit en une somme.

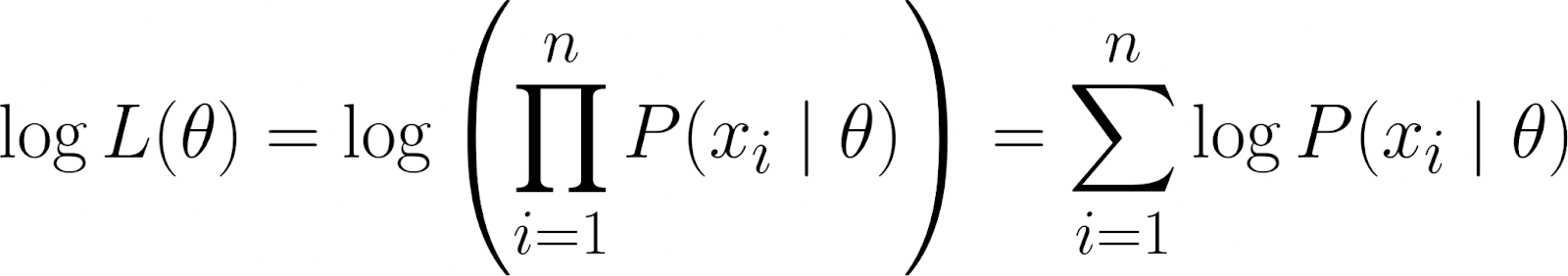
TCela nous donne la log-vraisemblance, qui présente certaines propriétés avantageuses :

• Le log transforme les produits en sommes, qui sont beaucoup plus faciles à manipuler, en particulier lors de la différenciation.
• La fonction logarithmique est monotone, donc maximiser la log-vraisemblance donne le même θ que maximiser la vraisemblance.

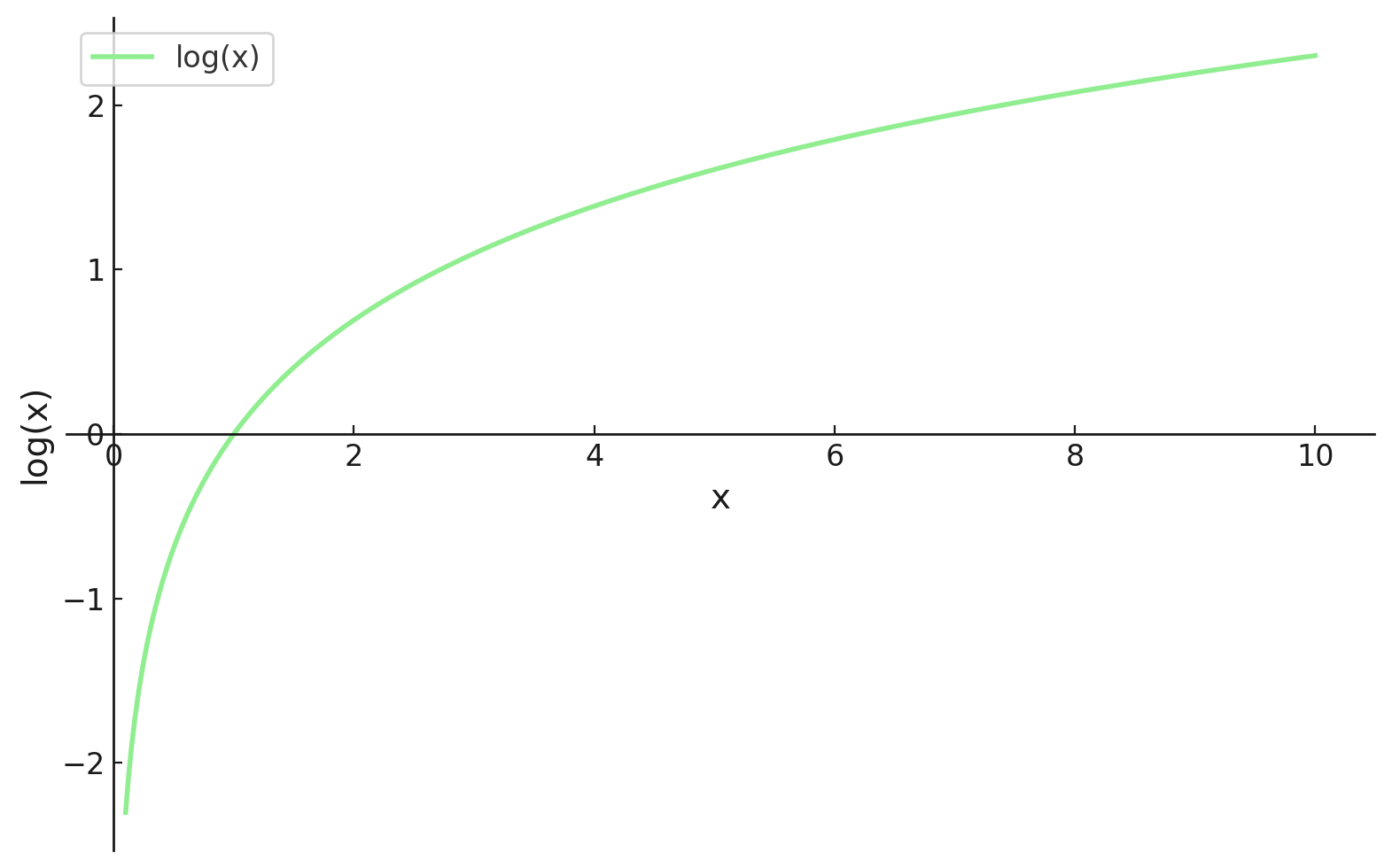
Étape 4 : Déterminer la valeur optimale

Nous sommes maintenant en mesure de faire la distinction, mais dans le domaine de l'apprentissage automatique, nous avons tendance à vouloir minimiser nos fonctions de perte. Heureusement, il est assez facile d'y remédier. 

En incluant un symbole moins (c'est-à-dire en multipliant par -1) au début de notre fonction, nous devons maintenant minimiser notre fonction de perte, qui s'appelle désormais la fonction de perte de log-vraisemblance négative.

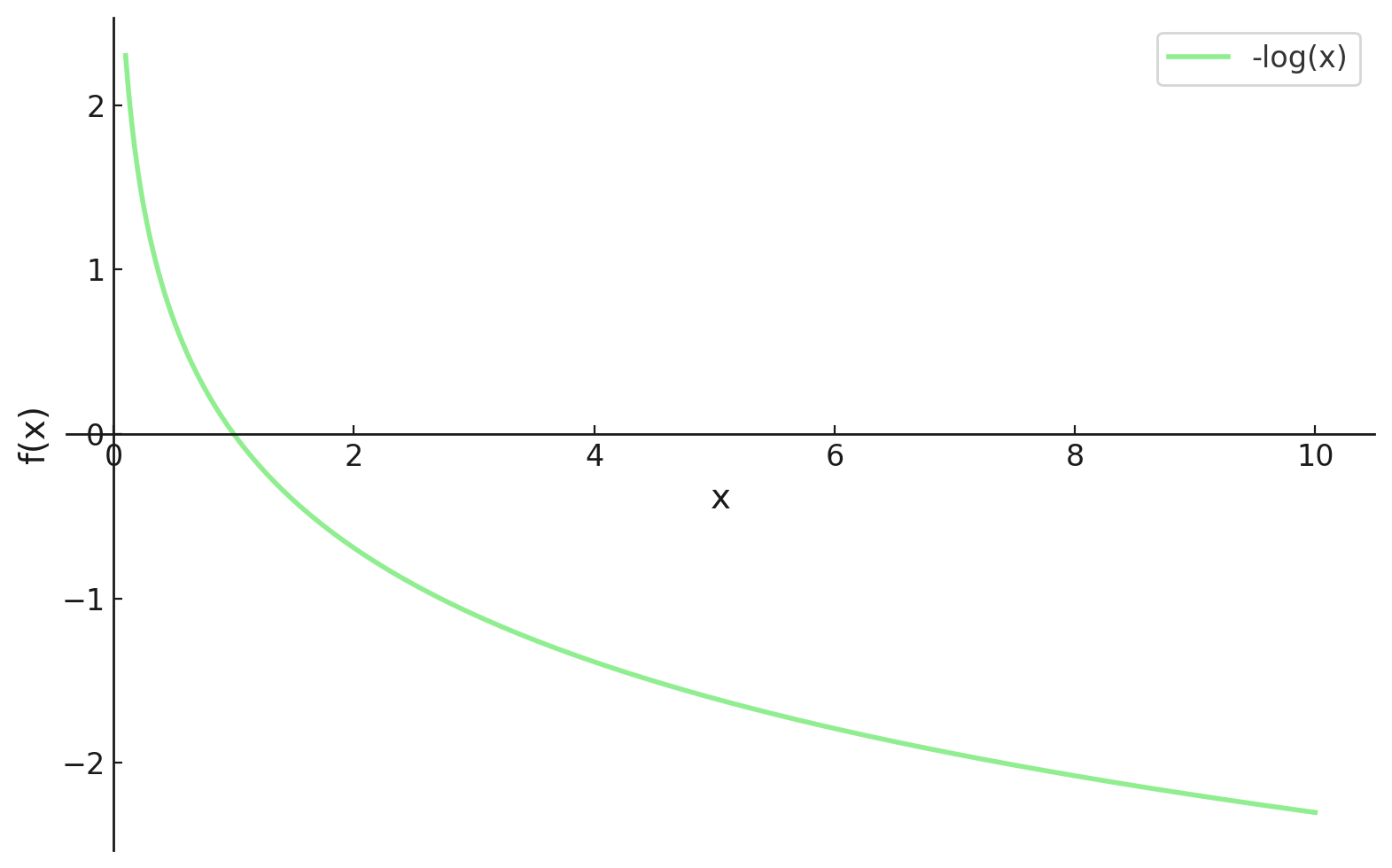
Maintenant, nous pouvons utiliser le calcul différentiel pour obtenir la valeur de θ. En dérivant la log-vraisemblance par rapport à θ, en la mettant à zéro et en résolvant pour θ. En effet, le minimum d'une fonction se trouve là où sa dérivée est nulle (et où la dérivée seconde est positive).

Par conséquent, l'équation finale pour MLE est la suivante :

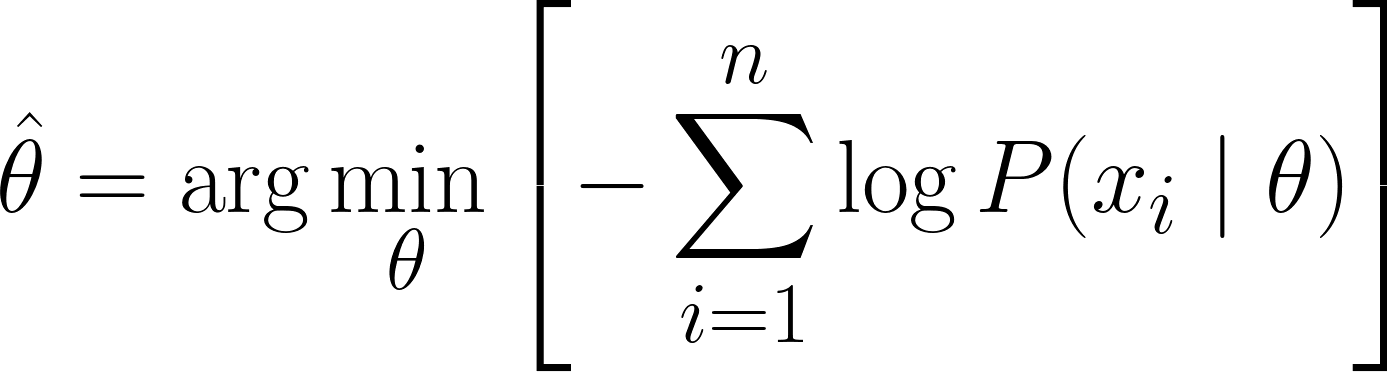
Exemples de MLE fonctionnels

Maintenant que nous avons réussi à dériver l'équation MLE, examinons quelques exemples pratiques pour consolider notre compréhension.

Exemple de lancers de dés

Commençons par un exemple simple et discret : estimer la probabilité d'obtenir un six avec un dé potentiellement biaisé.

Supposons que nous lancions un dé 12 fois et que nous enregistrions les résultats. Nous souhaitons modéliser ces données à l'aide d'unedistribution catégorielle d' , mais concentrons-nous sur l'estimation de la probabilité θ (thêta) d'obtenir un six. Dans cet exemple :

• Paramètre (θ) : Valeur que vous souhaitez estimer - Probabilité d'obtenir un six
• Données (x) : Les résultats observés : 4 six sur 12 lancers.

Nous calculons maintenant la fonction de vraisemblance, qui, comme nous avons obtenu 4 six sur 12 lancers, nous donne :

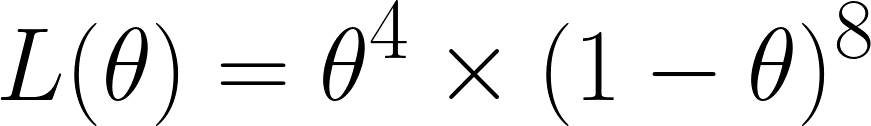
Nous avons obtenu ce résultat car, sur les 12 essais, nous avons obtenu 4 fois le chiffre 6, d'où le terme θ⁴, et 8 fois un autre chiffre, d'où le terme (1 - θ)⁸. 

Rappelons que nous avons multiplié car nous avons supposé qu'elles sont conditionnellement indépendants.

Nous prenons maintenant la log-vraisemblance négative comme nous l'avons vu précédemment, ce qui nous donne l'équation suivante :

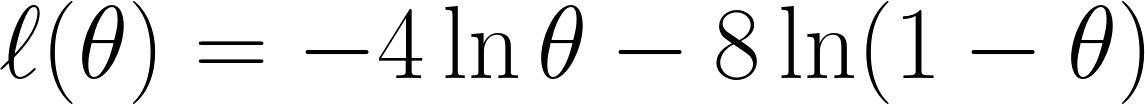
Enfin, nous dérivons l'équation avec par rapport à θ et la fixons à 0 (puisque nous voulons trouver le point minimum) :

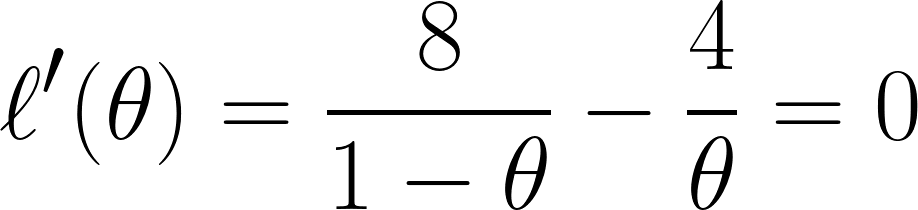
Grâce à cette équation, nous pouvons conclure que θ est égal à ⅓. 

Remarque : Si nous avions obtenu plusieurs solutions de θ, nous aurions également dû trouver la dérivée seconde et déterminer quelles valeurs de θ nous donneraient un résultat positif (afin de confirmer que nous avons trouvé un point minimum). Ceci peut être confirmé à l'aide d'un exemple de fonction dans l'image ci-dessous :

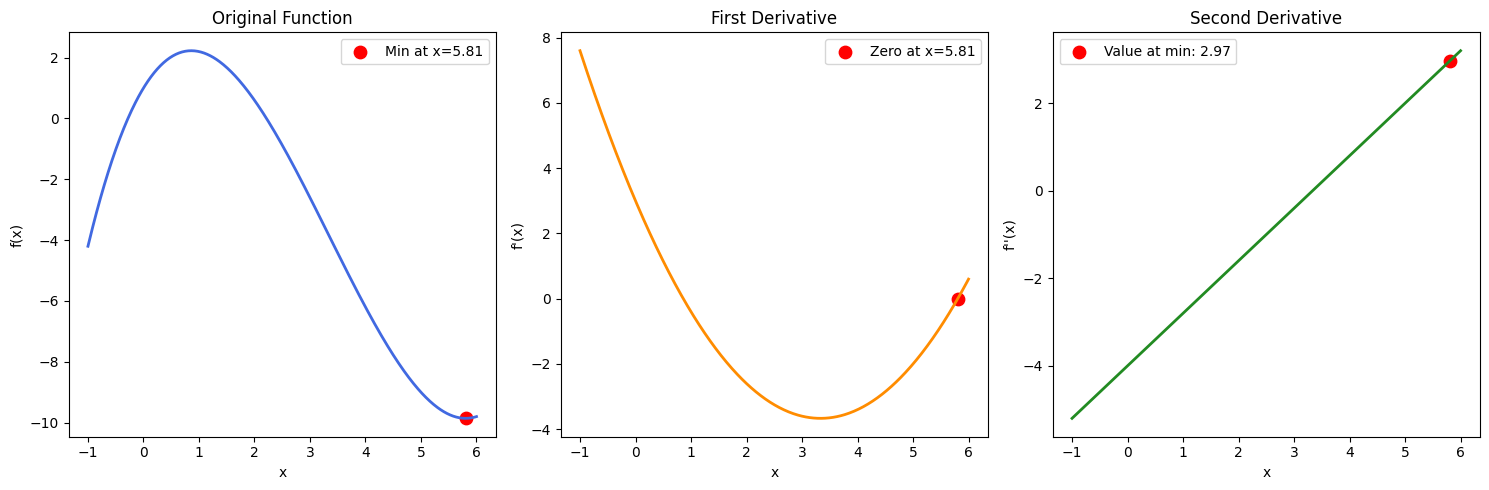
Exemple de hauteurs

Examinons maintenant un exemple continu : l'estimation de la moyenne d'une distribution normale (gaussienne).

Supposons que nous disposions d'un ensemble de données contenant la taille de 5 personnes : 160, 165, 170, 175, 180 (en cm). Nous supposerons également qu'ils sont tirés d'une distribution normale avecune moyenne μ (mu)inconnue et une variance σ² connue (disons σ² = 25 pour simplifier).

• Paramètre (μ) : La valeur que vous souhaitez estimer (la hauteur moyenne)
• Data (x₁, x₂, ..., x₅): Les hauteurs observées

La fonction de vraisemblance pour la distribution normale (avec variance connue) est la suivante. 

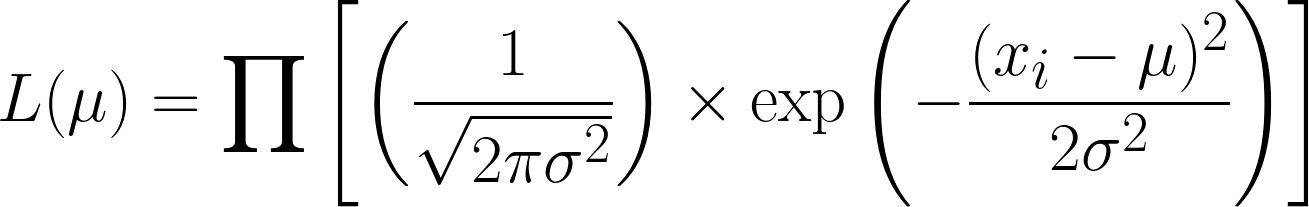
C'est très complexe, mais en prenant le logarithme négatif, cela devient plus simple. Nous espérons que vous comprenez désormais l'utilité de la fonction logarithmique dans notre équation. L'équation que nous obtenons est la suivante :

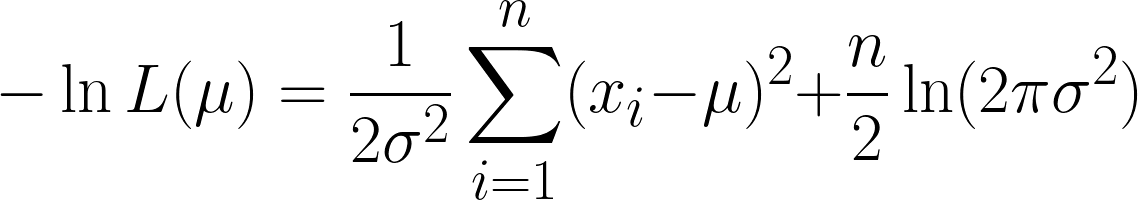
Nous obtenons ici deux termes, mais notez que le second peut être ignoré lorsque nous procédons à la dérivation, car nous différencions par rapport à μet que le deuxième terme ne contient pas μ.

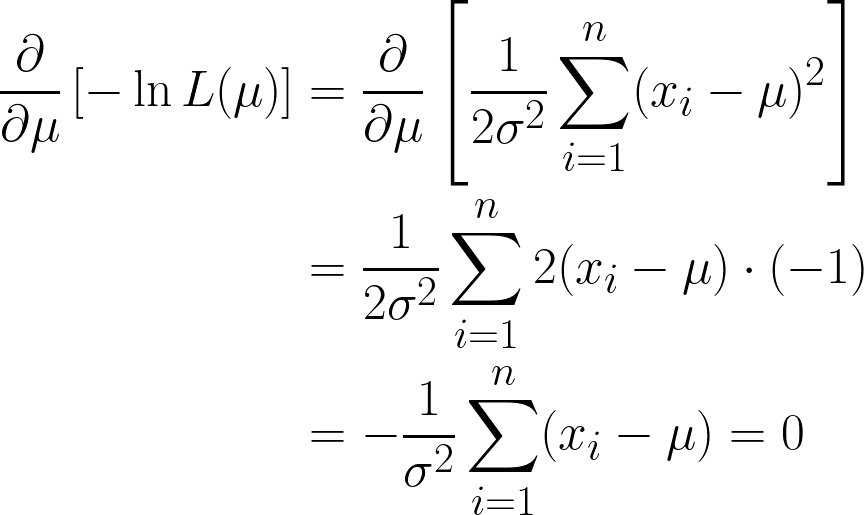
Nous y sommes presque, mais veuillez examiner μ entre parenthèses. 

Comme il s'agit d'un processus continu, il est important de vérifier régulièrement l'état constante, nous pouvons simplement la multiplier par n, car ajouter μ n fois équivaut simplement à n*μ.

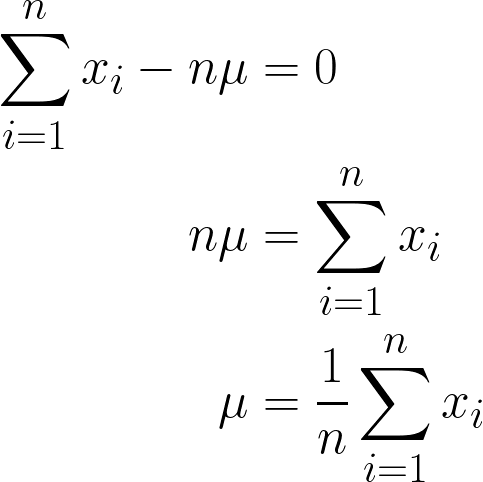
La réponse finale que nous avons obtenue devrait sembler intuitive, puisqu'elle est mathématiquement exprimée comme la somme de toutes les valeurs de x divisée par n (qui est le nombre d'observations dont nous disposons), ce qui correspond également à la définition de la moyenne. définition de la moyenne!

Ainsi, en intégrant les valeurs de nos données dans cette équation, nous obtenons une moyenne de 170 cm. 

Pour rendre cela plus clair, voici une animation illustrant comment la probabilité évolue lorsque nous modifions μ :

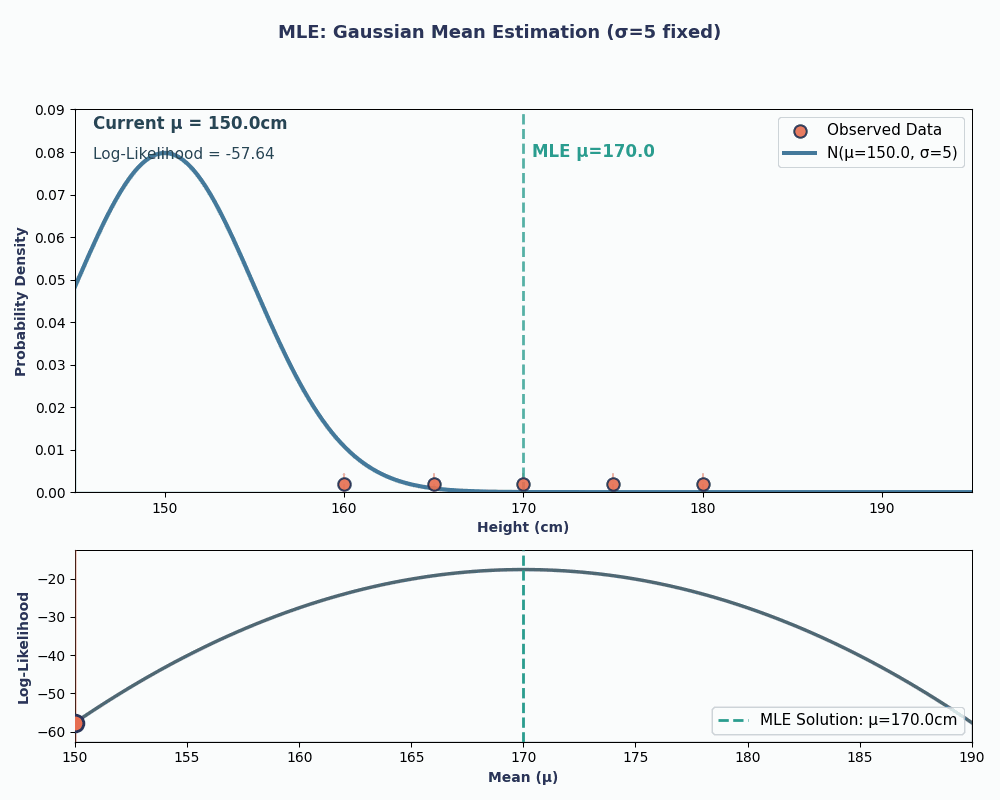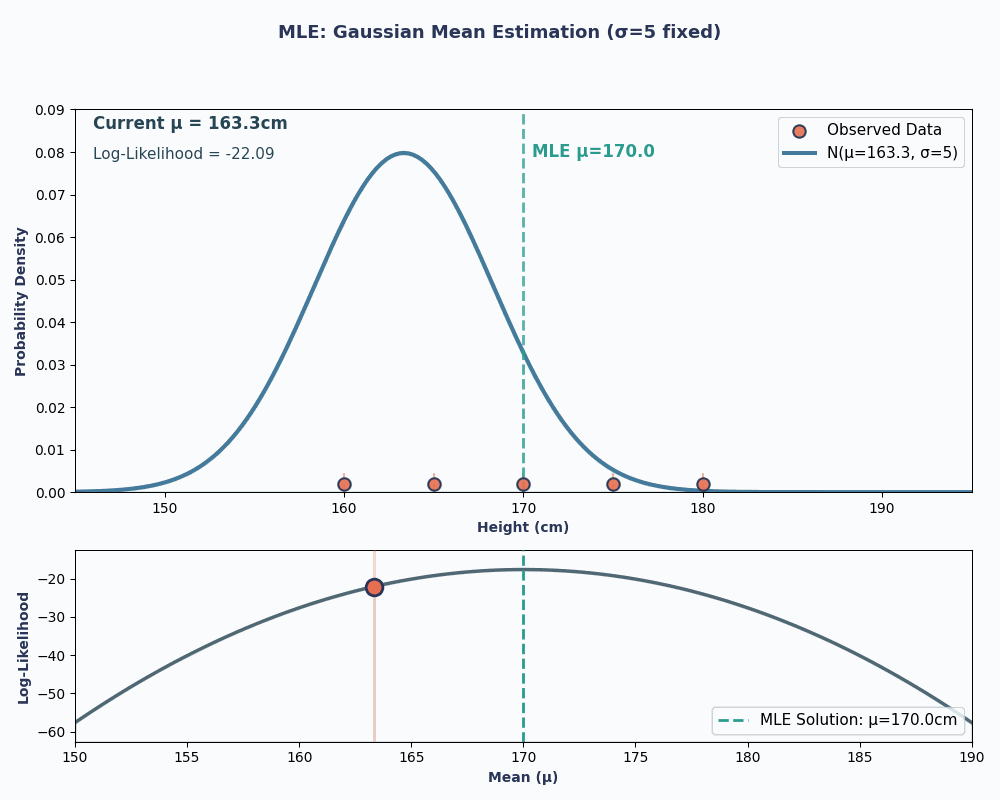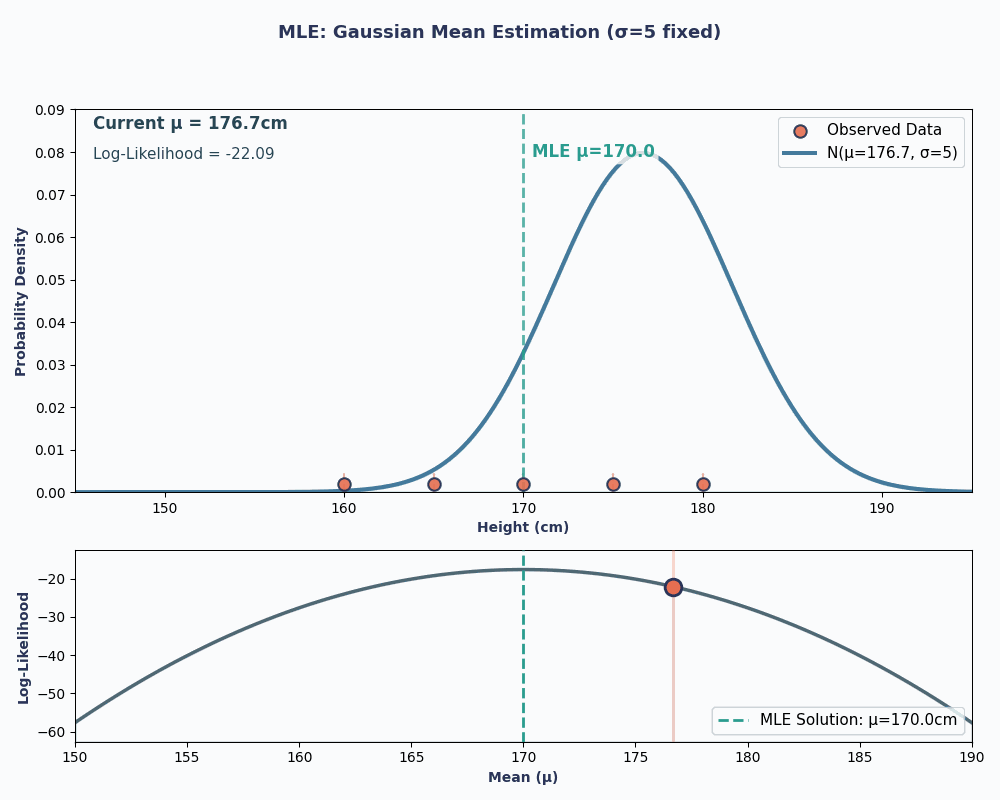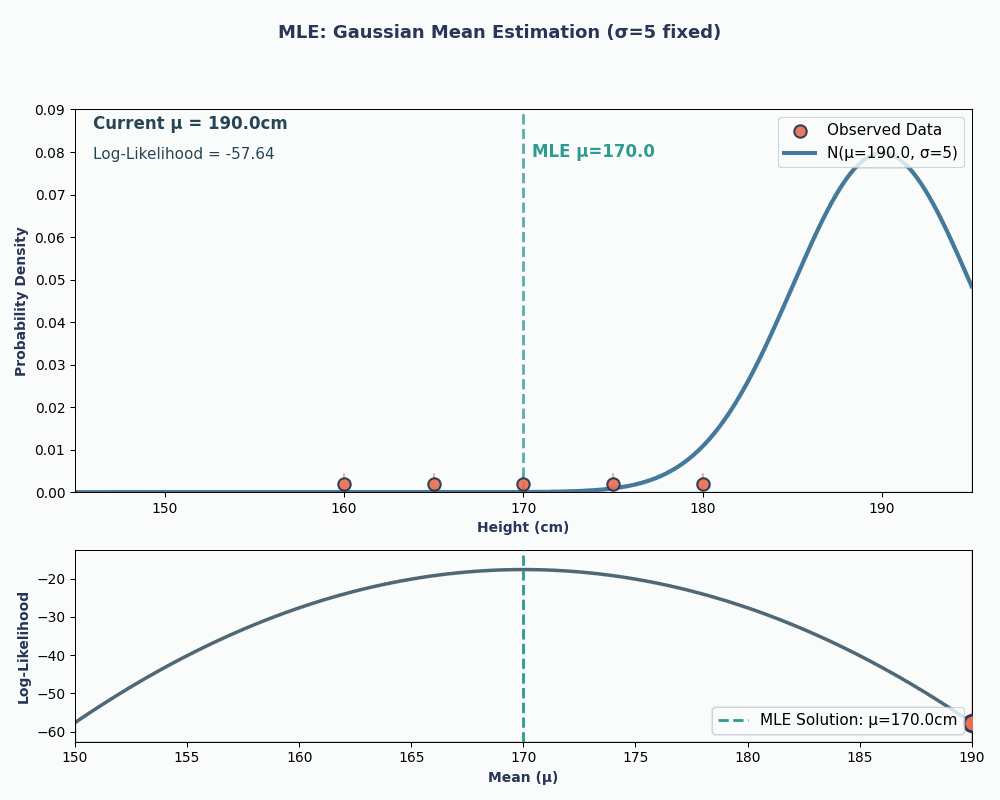
Dans les deux exemples, l'utilisation de la MLE nous a permis d'obtenir la valeur du paramètre qui rendait nos données observées les plus probables dans le modèle choisi. Il est évident que la MLE peutégalement fonctionner en nous fournissantplusieurs valeurs de paramètres d' , bien que le calcul soit légèrement plus long.

Codage MLE

Maintenant que nous avons compris la structure sous-jacente du MLE, voyons comment le coder en Python. Nous allons coder la solution de l'exemple précédent (hauteurs). 

# Importing libraries 
import numpy as np # used for handling arrays and mathematical operations.
from scipy.optimize import minimize # function that minimizes another function

# This is our sample data 
data = np.array([160, 165, 170, 175, 180])

# This was the variance we had assumed before
sigma_squared = 25

# Negative Log-Likelihood function
def negative_log_likelihood(mu):
    n = len(data) # Number of data points
    return 0.5 * n * np.log(2 * np.pi * sigma_squared) + \
           np.sum((data - mu)**2) / (2 * sigma_squared) # The NLL is for the Univariate Gaussian Distribution

# Optimizing the NLL
result = minimize(negative_log_likelihood, x0=170)  # initial guess

# Our final estimated mean
estimated_mu = result.x[0]
print(f"MLE estimate of mu: {estimated_mu}")

Stratégies et algorithmes informatiques

Veuillez noter que lorsque nous avons codé l'exemple précédent, nous avons créé une fonction negative_log_likelihood() qui contenait la logique principale pour calculer le MLE d'une distribution gaussienne univariée.

D'une part, on pourrait soutenir que nous avons finalement codé cette équation de manière rigide et que nous avons utilisé l'algorithme de minimisation de la fonction ( scipy.optimize ) pour minimiser cette fonction. Bien entendu, cette solution reste tout à fait viable, car la distribution gaussienne a une solution fermée. 

Explorons d'autres méthodes pour calculer des solutions pour MLE.

Solutions fermées et cas d'application

Comme nous l'avons vu précédemment, dans certains cas favorables, nous pouvons résoudre les équations MLE de manière analytique, ce qui signifie que nous pouvons dériver une formule exacte pour les estimations des paramètres. Cessolutions sont appeléessolutions fermées d' . Elles sont souvent simples, intuitives et rapides à coder et à calculer.

Une question importante à se poser maintenant est la suivante : quand existe-t-il des solutions fermées ?

1. Lorsque la fonction de vraisemblance logarithmique est dérivable, il est fonction de vraisemblance logarithmique est dérivable, concave et algébriquement traitable.
2. Lorsque le modèle est suffisamment simple, il est possible de déterminer le nombre de paramètres à utiliser assez simple, impliquant généralement un ou deux paramètres et aucune variable cachée.

Techniques d'optimisation numérique

Pour les modèles plus complexes, il n'existe pas de solutions analytiques ou celles-ci sont trop compliquées à dériver. Dans ces cas, nous utilisonsdes méthodes d'optimisation numérique d' , des algorithmes itératifs qui recherchent les paramètres qui maximisent la log-vraisemblance. Expliquons-les brièvement :

1. Méthode de Newton-Raphson : Cette méthode utilise les deux :

• La première dérivée (gradient) pour déterminer la pente, et
• La seconde dérivée (hessienne) pour mesurer la courbure et ajuster la taille du pas en conséquence.
• La règle de mise à jour est la suivante :
• Son principal avantage réside dans sa convergence rapide proche de l'optimum.
• Cependant, cela nécessite le calcul de dérivées secondes, qui peuvent être instables ou coûteuses dans les dimensions élevées.

2. Méthodes quasi-Newton (par exemple, BFGS) :

• Approximer la matrice hessienne en utilisant uniquement dérivées du premier ordre.
• Utilisé dans des bibliothèques populaires telles que scipy.optimize.minimize en Python (avec BFGS comme valeur par défaut).
• Plus numériquement stable et largement applicable que Newton-Raphson.

3. Algorithme d'optimisation des attentes (EM) :

• Technique d'optimisation spécialisée utilisée lorsque les données impliquent des variables latentes (cachées). variables latentes (cachées), c'est-à-dire des valeurs que nous ne pouvons pas observer directement, mais qui influencent les données.
• Cet algorithme comporte deux étapes :
• E-step (Attente) : Calculez la valeur attendue de la log-vraisemblance à l'aide des estimations actuelles des paramètres et des données observées.
• Étape M (maximisation) : Maximisez cette vraisemblance logarithmique attendue pour mettre à jour les estimations des paramètres.

Propriétés du MLE

Nos exemples et nos calculs démontrent clairement l'utilité de la MLE. D'un point de vue formel, la MLE présente les propriétés suivantes : 

1. Cohérence : À mesure que la taille de l'échantillon augmente, la MLE converge vers la valeur réelle du paramètre.
2. Normalité asymptotique : Pour les échantillons de grande taille, la distribution de la MLE devient approximativement normale (en forme de cloche) autour de la valeur réelle du paramètre. C'est la base pour construire des intervalles de confiance.
3. Efficacité : Parmi tous les estimateurs non biaisés, le MLE atteint la variance la plus faible possible (il atteint la borne inférieure de Cramér-Rao, au moins de manière asymptotique).
4. Invariance : Si θ̂ est le MLE pour θ, alors pour toute fonction g, g(θ̂) est le MLE pour g(θ). En d'autres termes, les MLE sont préservées lors des transformations.

Cependant, il existe des cas où l'utilisation de la MLE n'est pas la meilleure option :

1. Petits échantillons : La MLE peut être biaisée lorsque la taille de l'échantillon est petite. Par exemple, la MLE pour la variance (σ̂²) a tendance à sous-estimer la variance réelle (σ²).
2. Robustesse : La MLE est sensible aux valeurs aberrantes et aux erreurs de spécification du modèle. Des alternatives telles que les estimateurs M peuvent fournir des estimations plus robustes.
3. Alternative bayésienne : L'estimation a posteriori maximale (MAP) combine les informations préalables avec la vraisemblance, offrant une perspective bayésienne et parfois des estimations plus stables, en particulier lorsque les données sont limitées.

Applications dans le domaine de la modélisation statistique

Dans cette section, nous allons explorer les domaines dans lesquels le MLE est réellement utilisé dans le Machine Learning et l'IA.

Régression et classification

L'un des domaines les plus importants dans lesquels la MLE est utilisée est celui de la régression logistique. Ici, nous estimons la probabilité qu'un résultat appartienne à une certaine catégorie (telle que la perte d'un client) et nous le faisons en ajustant les paramètres àl' fin de maximiser la probabilité des résultats observés.

Même dans le cas d'une régression linéaire, si l'on suppose que les erreurs sont normalement distribuées, la solution des moindres carrés s'avère en fait être également la MLE.

Test d'hypothèses et sélection de modèles

La MLE peut également être utilisée pour comparer des modèles. 

Par exemple, le test du rapport de vraisemblance (LRT) nous aide à vérifier si l'ajout de variables supplémentaires à un modèle améliore significativement ses performances. Il fonctionne en comparant les probabilités de deux modèles : l'un plus simple (nul), l'autre plus complexe (alternatif).

Nous disposons également du critère d'information d'Akaike (AIC), qui pénalise la complexité afin d'éviter le surajustement. Ces outils sont largement utilisés dans des domaines tels que la finance, la médecine et le marketing.

Limites et alternatives à la MLE

Bien qu'il soit puissant, il présente certains inconvénients. Passons rapidement en revue ses points faibles et ce que nous pouvons utiliser à la place.

Principales limites de la MLE

• Sensible aux erreurs de spécification du modèle : Si notre modèle est incorrect (par exemple, si nous utilisons une distribution normale pour des données asymétriques), la MLE nous donnera des résultats trompeurs.
• Sensibilité aux valeurs aberrantes : Quelques données erronées peuvent complètement fausser vos estimations.
• Coût informatique : Pour les modèles de grande taille, en particulier ceux comportant de nombreux paramètres ou contraintes, l'optimisation de la vraisemblance peut s'avérer lente ou instable.
• Solutions multiples : Parfois, la surface de probabilité présente plusieurs pics (maxima locaux), ce qui complique la recherche de la meilleure solution.

Alternatives à l'estimation du maximum de vraisemblance

Lorsque la MLE ne fonctionne pas correctement, voici quelques options :

• MAP (Maximum a Posteriori) : Comme MLE, mais ajoute une croyance préalable. Cela peut contribuer à stabiliser les estimations lorsque les données sont limitées.
• Méthode des moments : Compare des moments échantillons (tels que la moyenne ou la variance) avec des moments théoriques. Il est moins précis que le MLE, mais très facile à calculer.
• Moins les carrés : Dans des cas tels que la régression linéaire avec des erreurs gaussiennes, les moindres carrés et la MLE sont identiques. Cependant, les moindres carrés peuvent toujours être utiles lorsque la MLE est trop complexe.

Différentes méthodes fonctionnent mieux dans différentes situations. Le MLE n'est peut-être pas toujours la solution, mais il constitue souvent un excellent point de départ.

Conclusion

L'estimation du maximum de vraisemblance est l'une des méthodes les plus naturelles et les plus utilisées pour l'estimation des paramètres. Il s'agit de rendre les données observéesaussi probables que possible, afin qu'elles puissent être utilisées dans de nombreux scénarios différents, tels que les lancers de pièces, les hauteurs gaussiennes, etc.

Le MLE s'adapte à différents modèles et évolue en fonction du volume de données, alliant élégance mathématique et puissance pratique. Bien qu'il présente certains inconvénients, en particulier avec des ensembles de données de petite taille ou désorganisés, il reste un outil fondamental pour l'apprentissage del' , du Machine Learning et de l'IA.

Si vous vous intéressez au machine learning, nous vous invitons à découvrir notre cursus Machine Learning Scientist in Python, qui explore le machine learning supervisé, non supervisé et profond. 

Êtes-vous prêt à approfondir vos connaissances sur l'estimation du maximum de vraisemblance à l'aide d'exercices pratiques ? Ces ressources peuvent vous aider à mettre en pratique vos connaissances et à acquérir une expérience pratique :

• Maximiser la vraisemblance, partie 1 (Python): Calculez et visualisez les vrais-probabilités afin de comprendre clairement comment les estimations des paramètres sont déterminées dans la pratique.
• Régression OLS : Les idées clés expliquées: Explorez le lien entre la régression par les moindres carrés ordinaires et la MLE en supposant des erreurs gaussiennes, ce qui renforce les concepts statistiques fondamentaux.
• Comprendre la régression logistique en Python: Découvrez comment la régression logistique exploite l'estimation du maximum de vraisemblances pour une classification et une estimation des paramètres efficaces.