T-Tests in R Tutorial: Lernen, wie man T-Tests durchführt

Bestimme mit t.test() in R, ob es einen signifikanten Unterschied zwischen den Mittelwerten der beiden Gruppen gibt.

Aktualisierte 11. Sept. 2024 · 10 Min. lesen

Einführung

Angenommen, du hast zwei Gruppen von Verkaufsteams und möchtest überprüfen, ob die durchschnittliche Anzahl der in einer Woche von beiden Teams verkauften Handys gleich ist oder nicht. Wie wirst du die Leistung vergleichen?

Du nimmst die durchschnittliche Anzahl der Mobiltelefone, die die jeweiligen Teams an 200 zufällige Kunden verkauft haben, und ermittelst die Differenz. Das erste Marketingteam hat im Durchschnitt 120 Handys verkauft, das zweite Team 80.

Es ist also klar, dass das erste Team im Verkauf besser abgeschnitten hat als das zweite Team. Richtig? Wir können nicht sicher sein, denn der Datensatz wird von zufälligen Kunden erhoben und repräsentiert nicht alle Personen, die das Telefon in dieser Woche gekauft haben.

Wie können wir also feststellen, welches Team besser abgeschnitten hat? Wir werden einen t-Test verwenden, um herauszufinden, ob der Unterschied zwischen den beiden Durchschnittswerten real ist oder nur Zufall.

Der t-Test ist eine statistische Hypothese, bei der Stichproben aus beiden Gruppen genommen werden, um festzustellen, ob es einen signifikanten Unterschied zwischen den Mittelwerten der beiden Gruppen gibt. Wie funktioniert das? Sie vergleicht sowohl den Stichprobenmittelwert als auch die Standardabweichung und berücksichtigt dabei den Stichprobenumfang und den Grad der Variabilität der Daten.

In diesem Tutorium lernen wir die Klassifizierung von t-Tests (t-Test mit einer Stichprobe, t-Test mit zwei Stichproben und t-Test mit gepaarten Stichproben) mit R-Codebeispielen kennen und lernen, die Ergebnisse zu interpretieren.

Hinweis: Wenn du neu in R bist, belege einen Minikurs Einführung in die R-Programmierung, um die Grundlagen zu verstehen.

Dein Weg zur Beherrschung von R

Beginne bei Null und baue dir grundlegende R-Kenntnisse für Data Science auf.

Kostenloses Lernen Beginnen

t.test() Function in R

Die Sprache R bietet uns eine einfache t. test-Funktion für t-Tests mit einer Stichprobe, zwei Stichproben und gepaarten Tests.

Es gibt zwei Möglichkeiten, die t.test-Funktion zu verwenden: die Standard- und die Formelmethode.

Standardmethode

Du gibst numerische Stichproben aus der x-Gruppe und der y-Gruppe an und gibst die Alternativhypothese, den hypothetischen Mittelwert mu und das Konfidenzniveau des Intervalls an. Außerdem kannst du einen gepaarten t-Test durchführen, indem du das Argument gepaart anklickst, und einen t-Test für zwei Stichproben mit gleicher Varianz, indem du das Argument var.equal änderst.

t.test(x, y,
      alternative = c("two.sided", "less", "greater"),
      mu = 0, paired = FALSE, var.equal = FALSE,
      conf.level = 0.95, ...)

Formel-Methode

Bei dieser Methode gibst du die Formel x~y an, wobei x ein numerischer Vektor oder eine Spalte aus den Daten und y eine binäre Spalte ist, die die Arten von Gruppen enthält.

t.test(formula, data, subset, na.action, ...)

Wie führe ich einen t-Test für eine Stichprobe in R durch?

Mit dem t-Test für eine Stichprobe wird statistisch geprüft, ob ein signifikanter Unterschied zwischen dem Stichprobenmittelwert und der Hypothese oder dem angenommenen Populationsmittelwert besteht. Der Test vergleicht den Stichprobenmittelwert mit dem Hypothesenmittelwert, wobei die Variabilität der Daten berücksichtigt wird.

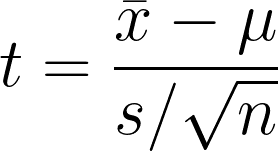
_x̄1 = Stichprobenmittelwert
μ = Hypothetischer Mittelwert der Bevölkerung
s = Standardabweichung der Stichprobe
n = Stichprobengröße

In diesem Tutorium werden wir den Datensatz "Kohlendioxidaufnahme bei Graspflanzen " als Beispiel für einen t-Test-Code verwenden. Der Datensatz hat 84 Zeilen und 5 Spalten und wurde bei einem Experiment zur Prüfung der Kältetoleranz der Grasart Echinochloa crus-galli erhoben. Wir werden bei unseren Tests hauptsächlich die Spalten Aufnahme, Behandlung und Typ berücksichtigen.

head(CO2)

In unserem Beispiel verwenden wir die Spalte conc (Kohlendioxidkonzentration) aus dem Datensatz.

Wir können den Mittelwert, die Verteilung und die Ausreißer mithilfe eines Boxplots beobachten.

boxplot(CO2$conc)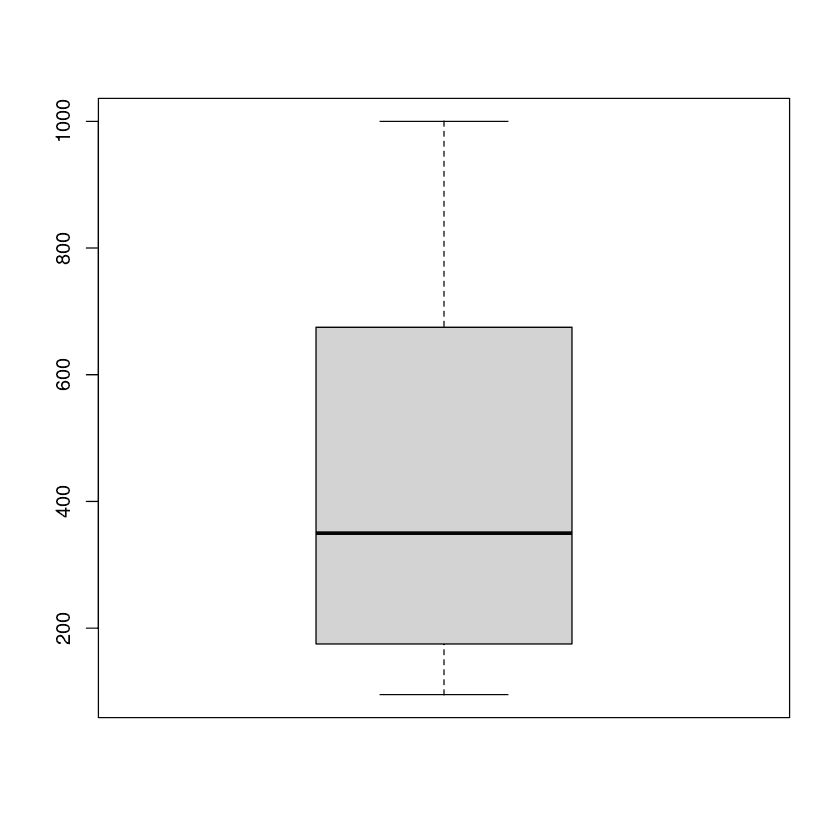

Für einen t-Test mit einer Stichprobe verwenden wir "t.test(x,mu=0)". Dabei ist x die Variable, mu wird durch die Nullhypothese festgelegt. In unserem Fall sind es 550.

t.test(CO2$conc, mu = 550)

Ergebnis:

Die Kohlendioxidkonzentration ist ungleich 550 und deutlich niedriger als der angenommene Bevölkerungsdurchschnitt.

One Sample t-test

data:  CO2$conc
t = -3.5617, df = 83, p-value = 0.0006134
alternative hypothesis: true mean is not equal to 550
95 percent confidence interval:
370.7805 499.2195
sample estimates:
mean of x
      435

Wie man einen t-Test mit zwei Stichproben in R durchführt

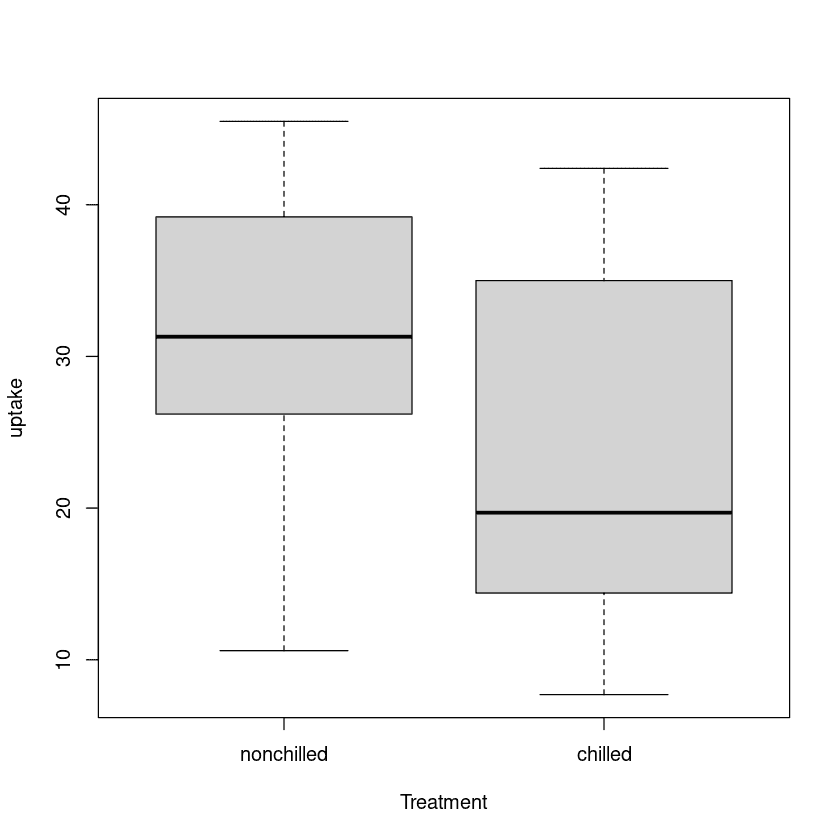
In den t-Tests mit zwei Stichproben werden wir die Kohlendioxid-Aufnahme von zwei Behandlungsarten vergleichen: nicht gekühlt und gekühlt.

Wir können die Verteilung von zwei Gruppen mit einem Boxplot visualisieren.

plot(uptake ~ Treatment, data=CO2)

Welch Zwei Stichproben t-Test

Sie ist eine statistische Hypothese, die untersucht, ob es einen signifikanten Unterschied zwischen den Mittelwerten zweier unabhängiger Gruppen gibt, die eine ungleiche Varianz haben können. Der Test vergleicht die Mittelwerte zweier Gruppen und berücksichtigt dabei die Variabilität innerhalb jeder Gruppe.

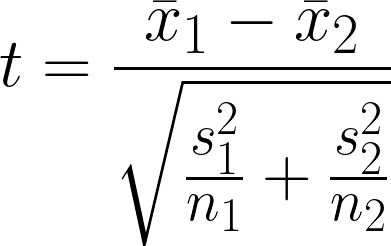
_x̄1 = Stichprobenmittelwert der ersten Gruppe
_x̄2 = Stichprobenmittelwert der zweiten Gruppe
_n1 = Stichprobengröße der ersten Gruppe
_n2 = Stichprobengröße der zweiten Gruppe
^s12 = Stichprobenvarianz der ersten Gruppe
^s22 = Stichprobenvarianz der zweiten Gruppe

Standardmäßig nimmt die Funktion t.test() an, dass die Varianz zweier Gruppen ungleich ist (var.equal=FALSE). Wir müssen also keine Änderungen vornehmen.

Wir verwenden die Formelmethode, um t-Testergebnisse zu erhalten, wobei Uptake ein numerischer Vektor und Treatment eine binäre Kategorienspalte des CO2-Datensatzes ist.

t.test(uptake ~ Treatment, data = CO2)

Ergebnis:

Es gibt einen signifikanten Unterschied zwischen den Mittelwerten der beiden Gruppen, und die nicht gekühlte Gruppe hat eine höhere Aufnahme als die gekühlte Gruppe.

 Welch Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 80.945, p-value = 0.003107
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.382366 11.336682
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333

Zwei Stichproben t-Test mit gleicher Varianz

Der t-Test für zwei Stichproben ist ein statistischer Hypothesentest, mit dem festgestellt werden kann, ob es einen signifikanten Unterschied zwischen den Mittelwerten zweier unabhängiger Gruppen gibt, wobei angenommen wird, dass die Varianz der beiden Gruppen gleich ist. Der Test vergleicht die Mittelwerte von zwei Gruppen und berücksichtigt dabei die Variabilität innerhalb jeder Gruppe.

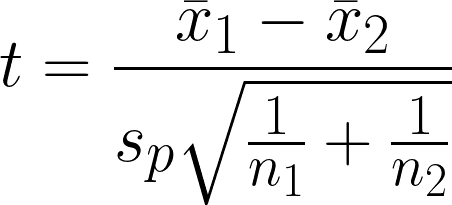
_x̄1 = Stichprobenmittelwert der ersten Gruppe
_x̄2 = Stichprobenmittelwert der zweiten Gruppe
_n1 = Stichprobengröße der ersten Gruppe
_n2 = Stichprobengröße der zweiten Gruppe
_sp = Gepoolte Standardabweichung

Um t-Tests mit zwei Stichproben und gleicher Varianz durchzuführen, müssen wir var.equal TRUE setzen und den Test mit derselben Formel und demselben Datensatz erneut durchführen.

t.test(uptake ~ Treatment, data = CO2, var.equal = TRUE)

Ergebnis:

Wie wir sehen können, haben wir fast ähnliche Ergebnisse erhalten, dass es einen signifikanten Mittelwertunterschied zwischen den beiden Gruppen gibt.

Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 82, p-value = 0.003096
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.38324 11.33581
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333

Wie man einen gepaarten t-Test in R durchführt

Der gepaarte t-Test ist eine statistische Hypothese, die verwendet wird, um festzustellen, ob es einen signifikanten Unterschied zwischen den Mittelwerten zweier verwandter oder gepaarter Stichproben gibt. Er berechnet den t-Test-Wert, indem er die Unterschiede zwischen den gepaarten Beobachtungen vergleicht und dabei die Variabilität innerhalb der Differenz berücksichtigt.

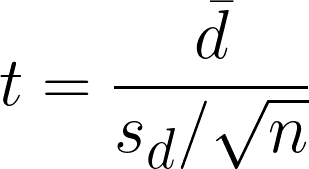
dࠡ = Differenzen der Mittelwerte bei gepaarten Beobachtungen
_sd = Differenzen der Standardabweichung der Stichprobe
n = Anzahl der Paare

Um einen gepaarten t-Test in R durchzuführen, müssen wir das Argument paired TRUE setzen und den Test mit derselben Formel und demselben Datensatz erneut durchführen.

t.test(uptake ~ Treatment, paired = TRUE, data = CO2)

Ergebnis:

Es gibt einen statistisch signifikanten Unterschied zwischen den Mittelwerten der beiden Gruppen, wenn man den t- und p-Wert betrachtet.

Paired t-test

data:  uptake by Treatment
t = 7.939, df = 41, p-value = 8.051e-10
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
5.114589 8.604458
sample estimates:
mean difference
      6.859524

Im zweiten Beispiel werden wir die Aufnahmerate für zwei Arten der gleichen Pflanze berechnen. Einer stammt aus Quebec, ein anderer aus Mississippi.

plot(uptake ~ Type, data=CO2)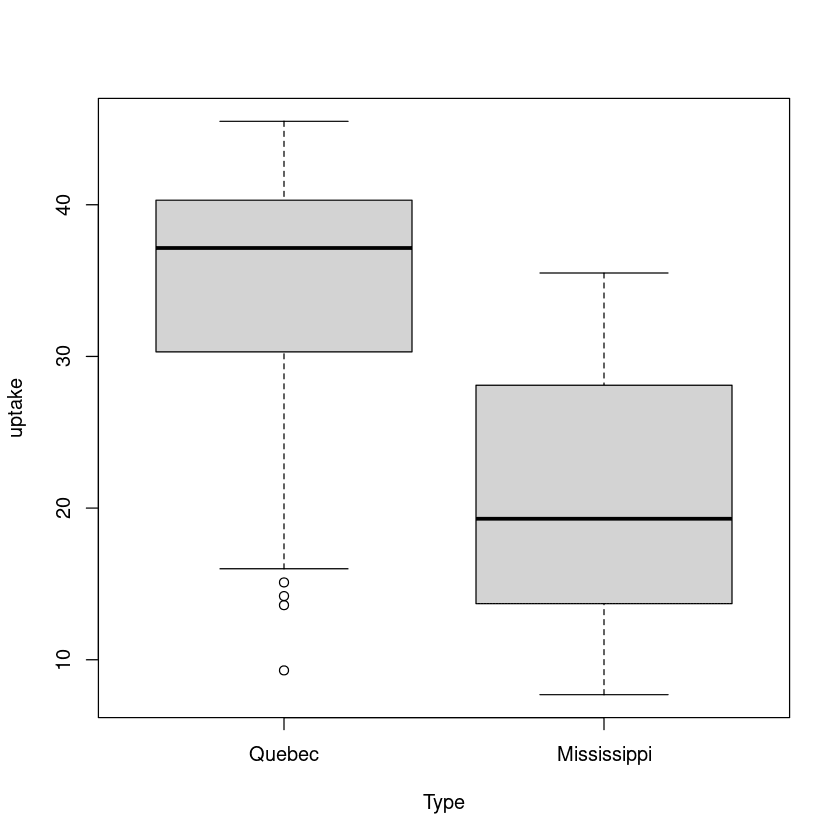

Überprüfen wir die Ergebnisse des gepaarten t-Tests, indem wir in der Formel Treatment durch den Typ ersetzen.

t.test(uptake ~ Type, paired = TRUE, data = CO2)

Ergebnis:

Auch hier gibt es einen signifikanten Unterschied zwischen dem Mittelwert der Quebecer und der Mississippi-Gruppe.

 Paired t-test

data:  uptake by Type
t = 11.374, df = 41, p-value = 2.937e-14
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
10.41177 14.90727
sample estimates:
mean difference
      12.65952

Probiere den t-Test im R DataLab Workbook aus. Es wird mit Code-Quellen und Ergebnissen geliefert. Du kannst die Arbeitsmappe auch duplizieren und an verschiedenen Beispielen üben.

Hinweis: Ein solides Statistik-Fundament wird dir gute Dienste leisten, ganz gleich, in welcher Branche du tätig bist. Statistik ist das Rückgrat der modernen KI, und du solltest deine Reise mit dem Skill Track Statistics Fundamentals with R beginnen.

Wie man t-Testergebnisse in R interpretiert

Wir generieren die Ergebnisse, aber was bedeuten df, p-Wert, Alternativhypothese oder Stichprobenschätzungen? In diesem Abschnitt lernen wir, wie man die Ergebnisse des t-Tests in R interpretiert.

Beginnen wir damit, zwei Gruppen mit der Funktion rnorm zu erstellen und den t-Test für zwei Stichproben durchzuführen.

set.seed(125)

group1 <- c(rnorm(100, mean = 24, sd = 3))
group2 <- c(rnorm(100, mean = 43, sd = 2.4))

t.test(group1, group2)

Ausgabe:

 Welch Two Sample t-test

data:  group1 and group2
t = -47.765, df = 179.99, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-19.51569 -17.96722
sample estimates:
mean of x mean of y
24.30063  43.04208

Daten: die Daten, die im Two Sample t-Test verwendet werden (Gruppe1 und Gruppe2)
t: t-Test-Statistik. Der negative t-Wert von -47,765 zeigt an, dass der Stichprobenmittelwert von Gruppe 1 deutlich kleiner ist als der von Gruppe 2.
df: Das ist der Freiheitsgrad, der mit dem t-Test-Wert verbunden ist.
p-Wert: gibt die statistische Signifikanz des Ergebnisses an. Der p-Wert liegt bei 2,2e-16 und damit unter Alpha (0,005), was bedeutet, dass die Wahrscheinlichkeit, einen so großen Unterschied zwischen den beiden Gruppen zufällig zu erhalten, sehr gering ist.
Alternativhypothese: Wir können die Alternativhypothese aufstellen. In unserem Fall wurde er so eingestellt, dass er prüft, ob die wahre Differenz der Mittelwerte ungleich Null ist.
95 Prozent Konfidenzintervall: 95% Zuversicht, dass der Unterschied zwischen den beiden Gruppen in der wahren Population innerhalb des Bereichs von -19,51569, -17,96722 liegt.
Stichprobenschätzungen: Sie geben uns die Stichprobenmittelwerte jeder Gruppe an, wobei Gruppe1 und Gruppe2 24,30063 bzw. 43,04208 betragen. Das bedeutet, dass Gruppe 2 im Durchschnitt einen höheren Wert hat als Gruppe 1.

Für den t-Test gibt es zwei Hypothesen:

_H0: _µ1 = _µ2: Die beiden Bevölkerungsmittelwerte sind gleich.
_HA: _µ1 _≠µ2: Die beiden Bevölkerungsmittelwerte sind nicht gleich.

Zusammenfassend lässt sich sagen, dass die Ergebnisse des Welch Two Sample t-Tests darauf hindeuten, dass es einen statistisch signifikanten Unterschied zwischen Gruppe1 und Gruppe2 gibt.

Fazit

In diesem Tutorium haben wir gelernt, wie man t-Tests mit einer Stichprobe, zwei Stichproben und gepaarten Stichproben mit R-Programmierbeispielen durchführt und wie man das Ergebnis interpretiert.

Der t-Test ist eines von vielen statistischen Werkzeugen, die bei Hypothesentests verwendet werden. Wenn du alles über Hypothesentests lernen willst, besuche den interaktiven Kurs Hypothesentests in R. Der Kurs behandelt t-Tests, ANOVA, Proportionstests und Chi-Quadrat-Tests.

Du kannst aber auch noch weiter gehen und dich für unseren Karrierepfad Statistiker/in mit R einschreiben, um die wichtigsten Fähigkeiten zu erlernen und einen Job als Statistiker/in zu bekommen.

Themen

R Programmierung

Datenanalyse