Tutorial sur les tests T dans R : Apprenez à réaliser des tests T

Fonction t.test() dans R

Le langage R nous fournit une fonction intégrée t.test simple pour les tests t à un échantillon, à deux échantillons et par paires. 

Il existe deux façons d'utiliser la fonction t.test : la méthode par défaut et la méthode de la formule. 

Méthode par défaut 

Vous fournissez des échantillons numériques du groupe x et du groupe y, en spécifiant l'hypothèse alternative, la moyenne mu supposée et le niveau de confiance de l'intervalle. En outre, vous pouvez effectuer un test t par paires en changeant l'argument paires et un test t à deux échantillons avec une variance égale en changeant l'argument var.equal.  

t.test(x, y,
      alternative = c("two.sided", "less", "greater"),
      mu = 0, paired = FALSE, var.equal = FALSE,
      conf.level = 0.95, ...)

Méthode de la formule

Dans cette méthode, vous fournissez la formule x~y, où x est un tableau numérique ou une colonne des données, et y une colonne binaire contenant les types de groupes.     

t.test(formula, data, subset, na.action, ...)

Comment réaliser un test t à un échantillon dans R

Le test t à un échantillon est l'hypothèse statistique permettant de tester s'il existe une différence significative entre la moyenne de l'échantillon et l'hypothèse ou la moyenne supposée de la population. Le test compare la moyenne de l'échantillon à la moyenne de l'hypothèse, tout en tenant compte de la variabilité des données. 

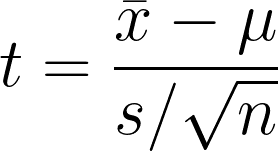
• _x̄1 = Moyenne de l'échantillon
• μ = Moyenne hypothétique de la population
• s = écart-type de l'échantillon
• n = Taille de l'échantillon

Dans ce tutoriel, nous utiliserons l'ensemble de données R sur l'absorption du dioxyde de carbone par les plantes herbacées pour des exemples de code de test t. L'ensemble de données comporte 84 lignes et 5 colonnes et a été collecté dans le cadre d'une expérience visant à tester la tolérance au froid de l'espèce de graminée Echinochloa crus-galli. Pour nos tests, nous tiendrons compte principalement des colonnes "absorption", "traitement" et "type". 

head(CO2)

Dans l'exemple, nous utiliserons la colonne conc (concentrations de dioxyde de carbone) de l'ensemble de données. 

Nous pouvons observer la moyenne, la distribution et les valeurs aberrantes à l'aide d'un diagramme en boîte. 

boxplot(CO2$conc)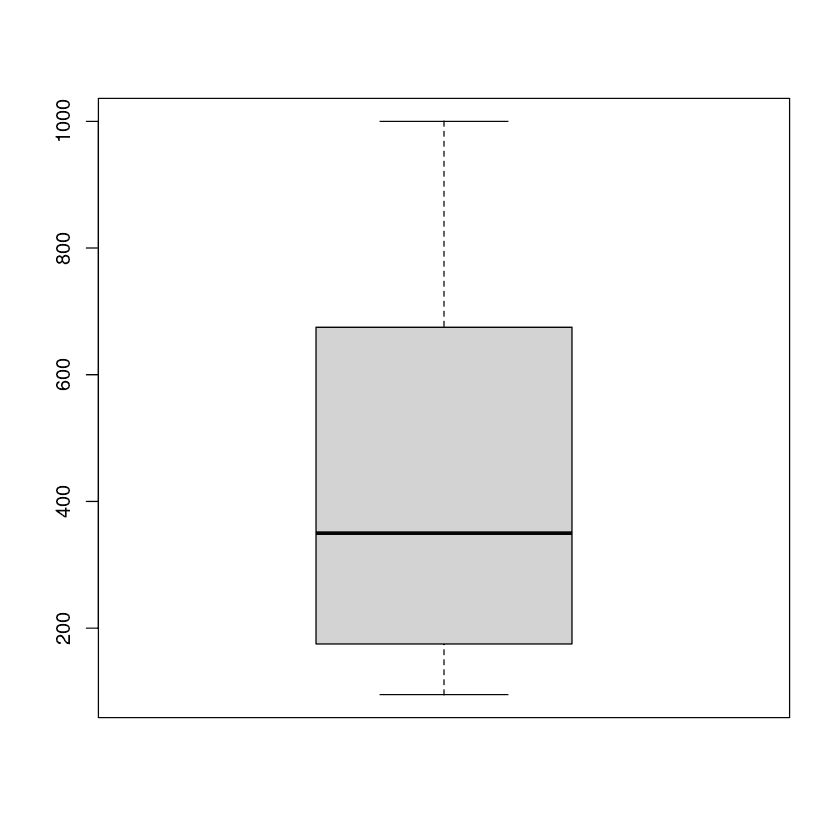

Pour un test t à un échantillon, nous utiliserons `t.test(x,mu=0)`. Où x est la variable, mu est défini par l'hypothèse nulle. Dans notre cas, il s'agit de 550. 

t.test(CO2$conc, mu = 550)

Résultat:

La concentration de dioxyde de carbone n'est pas égale à 550 et est significativement inférieure à la moyenne hypothétique de la population. 

One Sample t-test

data:  CO2$conc
t = -3.5617, df = 83, p-value = 0.0006134
alternative hypothesis: true mean is not equal to 550
95 percent confidence interval:
370.7805 499.2195
sample estimates:
mean of x
      435 

Comment réaliser un test t à deux échantillons dans R

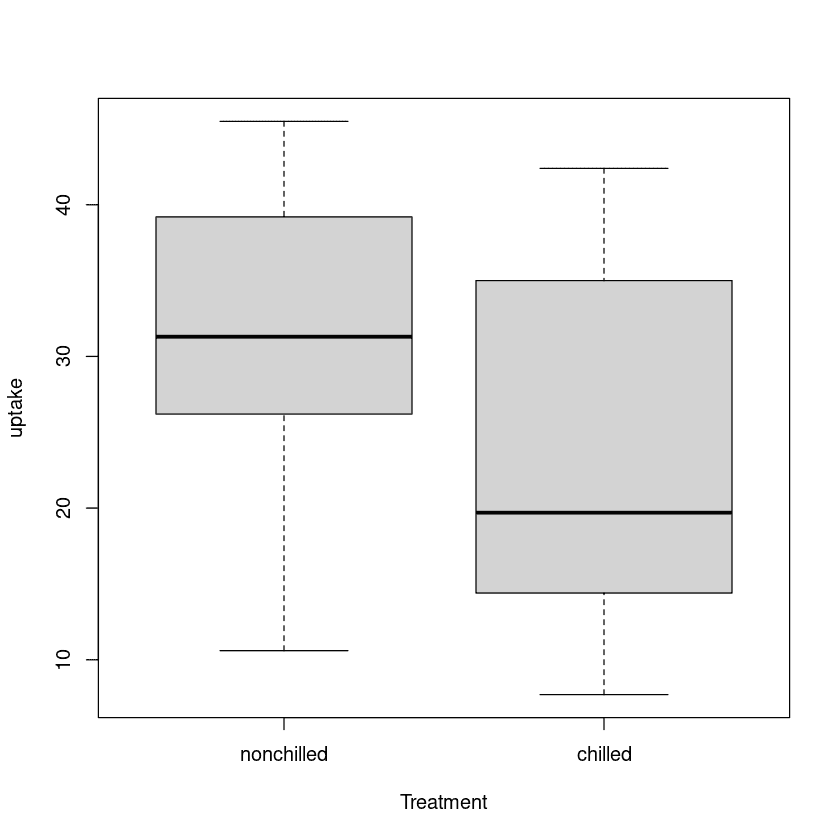
Dans les tests t à deux échantillons, nous comparerons les taux d'absorption de dioxyde de carbone de deux types de traitement : non réfrigéré et réfrigéré. 

Nous pouvons visualiser la distribution de deux groupes à l'aide d'un diagramme en boîte.  

plot(uptake ~ Treatment, data=CO2)

Test t de Welch à deux échantillons

Il s'agit d'une hypothèse statistique qui cherche à déterminer s'il existe une différence significative entre la moyenne de deux groupes indépendants dont la variance peut être inégale. Le test consiste à comparer les moyennes de deux groupes tout en tenant compte de la variabilité au sein de chaque groupe.  

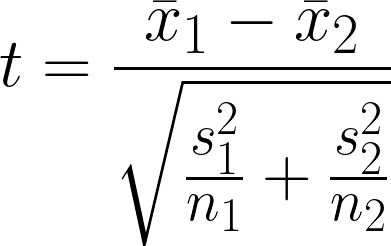
• _x̄1 = Moyenne de l'échantillon du premier groupe
• _x̄2 = Moyenne de l'échantillon du second groupe
• _n1 = Taille de l'échantillon du premier groupe
• _n2 = Taille de l'échantillon du deuxième groupe
• ^s12 = variance de l'échantillon du premier groupe
• ^s22 = variance de l'échantillon du deuxième groupe

Par défaut, la fonction t.test() suppose que la variance de deux groupes est inégale (var.equal=FALSE). Nous n'avons donc pas besoin de faire des changements. 

Nous utilisons la méthode de la formule pour obtenir les résultats du test t, où l 'absorption est un vecteur numérique et le traitement est une colonne de catégorie binaire de l'ensemble de données sur le CO2.  

t.test(uptake ~ Treatment, data = CO2)

Résultat:

Il y a une différence significative entre les moyennes des deux groupes, et le groupe non réfrigéré a un taux d'absorption plus élevé que le groupe réfrigéré. 

 Welch Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 80.945, p-value = 0.003107
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.382366 11.336682
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333  

Test t à deux échantillons avec variance égale

Le test t à deux échantillons est un test d'hypothèse statistique permettant de déterminer s'il existe une différence significative entre la moyenne de deux groupes indépendants, tout en supposant que la variance des deux groupes est égale. Le test compare les moyennes de deux groupes tout en tenant compte de la variabilité au sein de chaque groupe. 

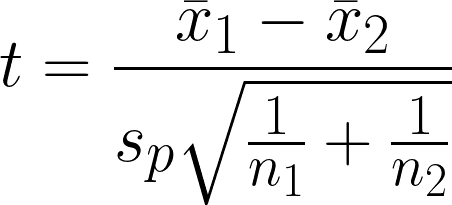
• _x̄1 = Moyenne de l'échantillon du premier groupe
• _x̄2 = Moyenne de l'échantillon du second groupe
• _n1 = Taille de l'échantillon du premier groupe
• _n2 = Taille de l'échantillon du deuxième groupe
• _sp = Écart-type regroupé

Pour effectuer des tests t à deux échantillons avec une variance égale, nous devons définir var.equal TRUE et exécuter le test à nouveau avec la même formule et le même ensemble de données.

t.test(uptake ~ Treatment, data = CO2, var.equal = TRUE)

Résultat:

Comme nous pouvons le voir, nous avons obtenu des résultats presque similaires, à savoir qu'il existe une différence moyenne significative entre les deux groupes.

Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 82, p-value = 0.003096
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.38324 11.33581
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333

Comment réaliser un test t par paires dans R

Le test t par paires est une hypothèse statistique utilisée pour déterminer s'il existe une différence significative entre les moyennes de deux échantillons liés ou appariés. Il calcule la valeur du test t en comparant les différences entre les observations appariées tout en tenant compte de la variabilité au sein de la différence. 

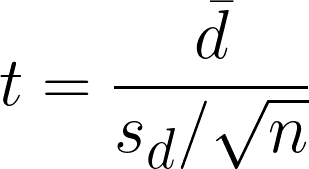
• dࠡ = différences de moyenne dans les observations appariées
• _sd = différences de l'écart-type de l'échantillon
• n = nombre de paires

Pour effectuer un test t pairé dans R, nous devons définir l'argument paired comme VRAI et exécuter le test à nouveau avec la même formule et le même ensemble de données.

t.test(uptake ~ Treatment, paired = TRUE, data = CO2)

Résultat:

Il existe une différence statistiquement significative entre les moyennes des deux groupes si l'on considère les valeurs t et p. 

Paired t-test

data:  uptake by Treatment
t = 7.939, df = 41, p-value = 8.051e-10
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
5.114589 8.604458
sample estimates:
mean difference
      6.859524 

Dans le deuxième exemple, nous allons factoriser le taux d'absorption pour deux types de la même plante. L'un est originaire du Québec, l'autre du Mississippi.

plot(uptake ~ Type, data=CO2)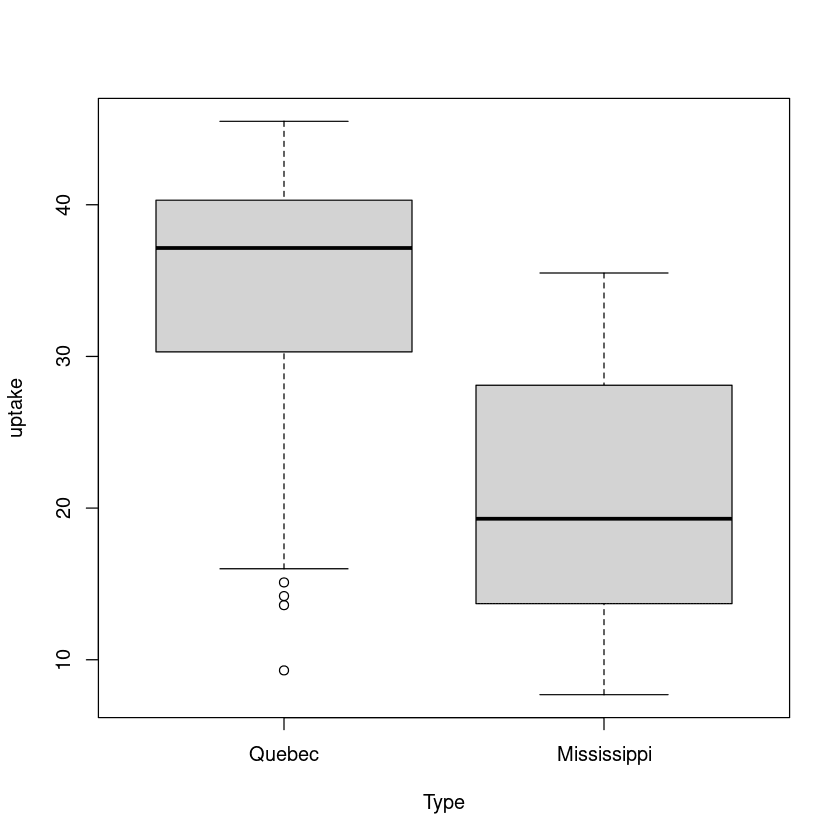

Vérifions les résultats du test t apparié en remplaçant le traitement par le type dans la formule. 

t.test(uptake ~ Type, paired = TRUE, data = CO2)

Résultat:

Là encore, il existe une différence significative entre la moyenne du groupe du Québec et celle du groupe du Mississippi. 

 Paired t-test

data:  uptake by Type
t = 11.374, df = 41, p-value = 2.937e-14
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
10.41177 14.90727
sample estimates:
mean difference
      12.65952  

Essayez le test t dans R DataLab Workbook. Il est accompagné de sources de code et de résultats. Vous pouvez également dupliquer le cahier d'exercices et commencer à vous entraîner sur différents exemples. 

Note: Des bases solides en statistiques vous seront utiles, quel que soit le secteur d'activité auquel vous appartenez. Les statistiques sont l'épine dorsale de l'IA moderne, et vous devriez commencer votre parcours en suivant le cursus Statistics Fundamentals with R skill track.

Comment interpréter les résultats d'un test t dans R

Nous générons les résultats, mais que signifient df, p-value, hypothèse alternative ou estimations de l'échantillon ? Dans cette section, nous allons apprendre à interpréter les résultats du test t dans R. 

Commençons par créer deux groupes à l'aide de la fonction rnorm et exécutons les tests t à deux échantillons. 

set.seed(125)

group1 <- c(rnorm(100, mean = 24, sd = 3))
group2 <- c(rnorm(100, mean = 43, sd = 2.4))

t.test(group1, group2)

Sortie:

 Welch Two Sample t-test

data:  group1 and group2
t = -47.765, df = 179.99, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-19.51569 -17.96722
sample estimates:
mean of x mean of y
24.30063  43.04208 

• données: les données utilisées dans le test t à deux échantillons (groupe1 et groupe2) 
• t: t test-statistique. La valeur t négative de -47,765 indique que la moyenne de l'échantillon du groupe 1 est significativement inférieure à celle du groupe 2.
• df: c'est le degré de liberté associé à la valeur du test t.
• Valeur p: indique la signification statistique du résultat. La valeur p est de 2,2e-16, ce qui est inférieur à alpha (0,005), ce qui indique que la probabilité d'obtenir une différence aussi importante entre les deux groupes par hasard est très faible.
• hypothèse alternative: nous pouvons définir l'hypothèse alternative. Dans notre cas, il a été défini pour vérifier si la différence réelle des moyennes n'est pas égale à zéro.
• Intervalle de confiance de 95 % : 95% de confiance que la vraie population signifie que la différence entre les deux groupes se situe entre -19,51569 et -17,96722.
• estimations de l'échantillon: il nous indique les moyennes de l'échantillon de chaque groupe, le groupe 1 et le groupe 2 étant respectivement de 24,30063 et 43,04208. Cela signifie qu'en moyenne, le groupe 2 a une valeur plus élevée que le groupe 1. 

Il y a deux hypothèses pour le test t :

1. _H0: _µ1 = _µ2: les deux moyennes de population sont égales.
2. _HA: _{µ1 ≠µ2}: les deux moyennes de population ne sont pas égales.

En conclusion, les résultats du test t de Welch à deux échantillons suggèrent qu'il y a de fortes chances qu'il y ait une différence statistiquement significative entre le groupe 1 et le groupe 2. 

Conclusion 

Dans ce tutoriel, nous avons appris à connaître les tests t à un échantillon, à deux échantillons et par paires avec des exemples de programmation R et comment interpréter les résultats. 

Le test t est l'un des nombreux outils statistiques utilisés dans les tests d'hypothèse. Si vous souhaitez tout savoir sur les tests d'hypothèse, suivez un cours interactif sur les tests d'hypothèse en R. Le cours couvre les tests t, l'ANOVA, les tests de proportion et les tests du chi carré.

Vous pouvez également aller plus loin et vous inscrire à notre cursus de carrière Statisticien avec R pour maîtriser les compétences essentielles et décrocher un emploi de statisticien.