Kurs
Wenn wir viele Zufallsstichproben aus so ziemlich jeder Art von Datenverteilung nehmen, passiert etwas Überraschendes. Der Durchschnitt dieser Stichproben sieht aus wie eine Normalverteilung - die bekannte Glockenkurve. Das ist der zentrale Grenzwertsatz (CLT) in einer Nussschale.
In der Wahrscheinlichkeitsrechnung und Statistik ist das eine große Sache, denn es bedeutet, dass wir genaue Vorhersagen treffen und Rückschlüsse auf ganze Populationen ziehen können, auch wenn wir nur kleine Stichproben betrachten.
Was die CLT besonders nützlich macht, ist, dass sie auch dann funktioniert, wenn die ursprünglichen Daten nicht normal verteilt sind. Lass uns das im Detail untersuchen und sehen, wie wir es berechnen können.
Was ist der zentrale Grenzwertsatz?
Der zentrale Grenzwertsatz (CLT) ist eine Idee aus der Statistik, die besagt, dass, wenn wir eine Reihe von Zufallsstichproben aus einer beliebigen Population nehmen und den Durchschnitt dieser Stichproben betrachten, diese Durchschnittswerte eine normale, glockenförmige Kurve bilden, auch wenn die ursprüngliche Population überhaupt nicht normal aussieht.
Dies hängt mit dem Gesetz der großen Zahlen zusammen, das besagt, dass der Durchschnitt unserer Stichprobe immer näher an den wahren Durchschnitt der gesamten Bevölkerung herankommt, je mehr Daten wir sammeln. Die CLT geht noch einen Schritt weiter - sie sagt uns, dass der Stichprobendurchschnitt genauer wird und dass das Muster dieser Durchschnitte vorhersehbar wird. In unserem Kurs "Einführung in die Statistik" gibt es praktische Übungen, um dich mit der Beziehung und den Unterschieden zwischen der CLT und dem Gesetz der großen Zahlen vertraut zu machen, falls du diesen Teil weiter vertiefen möchtest.
Eine gute Möglichkeit, dies in Aktion zu sehen, ist, einen Würfel zu werfen. Wenn wir sie nur einmal würfeln, erhalten wir eine Zufallszahl zwischen 1 und 6. Aber nach genügend Würfen wird sich der Durchschnitt bei 3,5 einpendeln (der wahre Durchschnittswert eines fairen Würfels). Wenn du das wiederholt machst, sieht die Verteilung der Durchschnittswerte wie eine normale Kurve aus.
Formel des zentralen Grenzwertsatzes
Hier ist die Grundformel für den zentralen Grenzwertsatz:
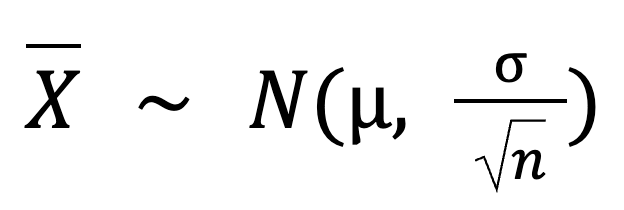
In dieser Formel:
-
Xist die Stichprobenverteilung des Stichprobenmittelwerts, die einer Normalverteilung folgt. -
Nist die Normalverteilung. -
𝜇ist der Mittelwert der Bevölkerung. -
σist die Standardabweichung der Bevölkerung. -
nist der Stichprobenumfang.
Je größer die Stichprobe ist, desto kleiner wird die Standardabweichung der Stichprobenverteilung. Je mehr Daten wir sammeln, desto enger werden sich unsere Stichprobenmittelwerte um den wahren Mittelwert der Grundgesamtheit gruppieren.
Bedingungen des zentralen Grenzwertsatzes
Damit der zentrale Grenzwertsatz so funktioniert, wie wir es erwarten, gibt es einige Bedingungen zu beachten:
- Ausreichend großer Stichprobenumfang: Die Stichprobengröße muss groß genug sein. Eine Stichprobengröße von 30 oder mehr gilt normalerweise als gut. Aber wenn die Grundgesamtheit, aus der wir eine Stichprobe ziehen, schief ist oder viele Ausreißer hat, brauchen wir vielleicht eine größere Stichprobe, um die schöne, glockenförmige Kurve zu sehen.
- Unabhängige und identisch verteilte (i.i.d.) Stichproben: Die Stichproben, die wir nehmen, müssen unabhängig und identisch verteiltsein (i.i.d.). Das bedeutet, dass jede Stichprobe zufällig ausgewählt wird und aus der gleichen Grundgesamtheit stammt. Wenn das nicht der Fall ist, sind die Ergebnisse möglicherweise nicht zuverlässig.
- Endliche Bevölkerungsvarianz: Die Grundgesamtheit, aus der wir eine Stichprobe ziehen, muss eine endliche Varianz haben. Wenn die Daten aus einer Verteilung mit unendlicher Varianz stammen, wie z. B. der Cauchy-Verteilung, gilt die CLT nicht für sie.
Beispiele des zentralen Grenzwertsatzes
Nehmen wir an, wir wollen wissen, wie viele Tassen Kaffee pro Tag in einem örtlichen Coffee Shop verkauft werden. Im Laufe der Jahre kann die Anzahl der täglich verkauften Becher einer ähnlichen Verteilung folgen wie die, die ich hier einfüge. An den meisten Tagen werden zwischen 80 und 120 Becher verkauft. Aber an Tagen, an denen viel los ist, wie z.B. an Feiertagen oder bei besonderen Veranstaltungen, verkaufen sie 150 oder sogar 180 Becher. Die Daten sind in diesem Fall ein bisschen schief (ungleichmäßig).
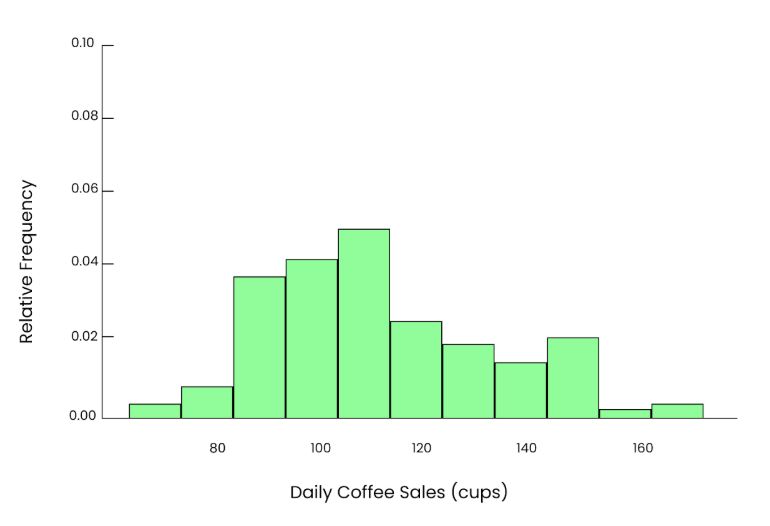
Ungleiche Grafik. Bild vom Autor.
Nehmen wir mal eine kleine Stichprobe. Wir wählen zufällig 5 Tage aus dem Jahr aus und schauen, wie viele Becher an diesen Tagen verkauft wurden.
95, 102, 85, 110, 120Der Mittelwert, den wir aus dieser Stichprobe erhalten, ist:
Mean = 95+102+85+110+1205 = 102.4 cups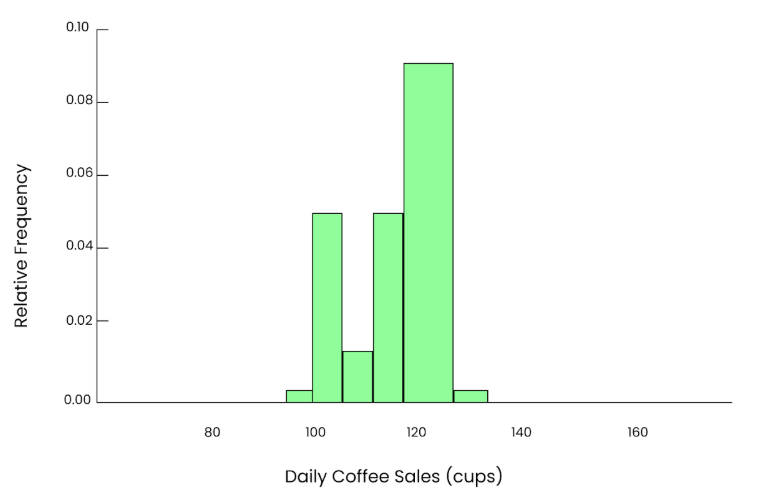
Grafik von 5 Tassen. Bild vom Autor.
So erhalten wir eine Schätzung des Mittelwerts der Grundgesamtheit, aber da die Stichprobe klein ist, ist sie möglicherweise nicht genau. Wenn wir diesen Vorgang 10 Mal wiederholen, wählen wir jedes Mal 5 Tage zufällig aus, berechnen den Mittelwert und schreiben die Ergebnisse auf. Die Mittelwerte der 10 Stichproben wären:
97.6, 105.8, 93.4, 110.2, 99.0, 102.4, 101.2, 107.5, 96.3, 94.1Wenn wir diese Werte in ein Histogramm eintragen, sehen wir eine grobe Glockenform, die aber trotzdem ungleichmäßig aussieht. Und die Streuung dieser Mittelwerte ist kleiner als die Streuung in der Bevölkerung.
Grafik von 10 Tassen. Bild vom Autor.
Nehmen wir jetzt eine größere Stichprobe. Dieses Mal wählen wir zufällig 50 Tage aus und berechnen die durchschnittliche Anzahl der verkauften Becher:
98, 104, 87, 112, 105, 100, 108, 95, 102, 106,
92, 115, 97, 101, 109, 103, 96, 110, 104, 98,
100, 102, 89, 107, 94, 111, 108, 90, 100, 103,
106, 99, 96, 112, 105, 97, 100, 104, 93, 110,
107, 102, 95, 101, 99, 103, 109, 98, 94, 100Wenn wir den Mittelwert dieser Stichprobe berechnen, erhalten wir:
Mean = 101.2 cupsDiese Schätzung liegt viel näher am Mittelwert der Bevölkerung von 100, und weil unsere Stichprobe größer ist, ist es eine genauere Schätzung.
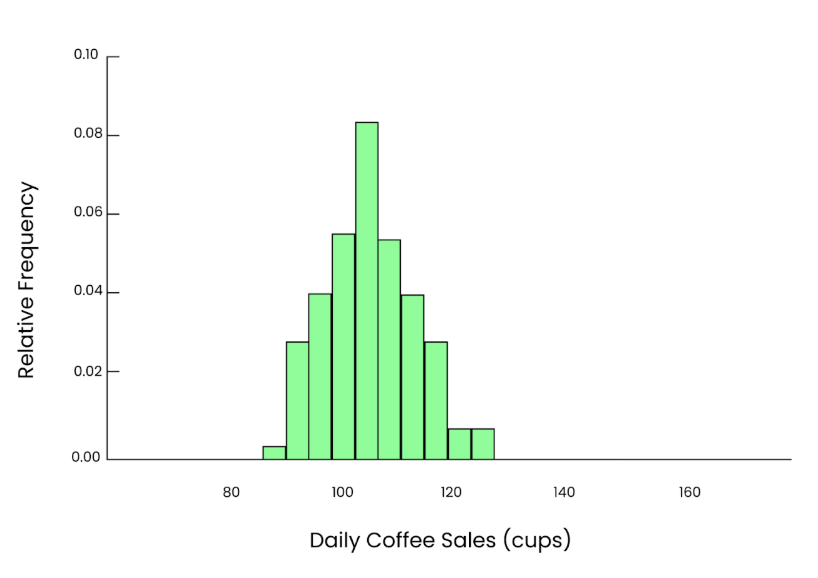
Wenn wir diesen Vorgang viele Male wiederholen, jedes Mal 50 Tage zufällig auswählen, den Mittelwert berechnen und diesen Mittelwert in einem Histogramm auftragen, sehen wir eine scheinbar glatte, glockenförmige Kurve, obwohl die ursprünglichen Daten schief waren. Das ist also die Macht des zentralen Grenzwertsatzes.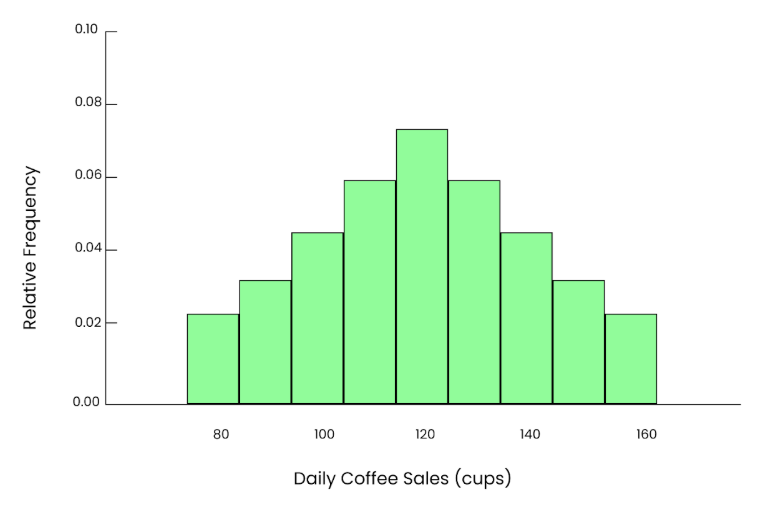
Gerade Grafik. Bild vom Autor.
Wir können diese Spanne sogar mit dieser Formel berechnen:
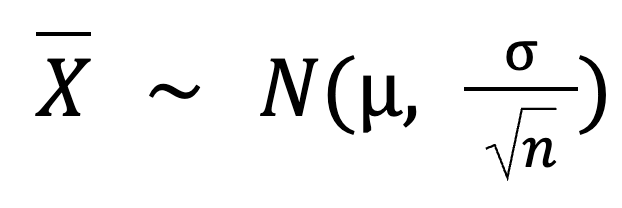 Hier:
Hier:
-
µ(Mittelwert der Bevölkerung) = 100 -
σ(Standardabweichung der Bevölkerung) = 15 -
n(Stichprobengröße) = 50
Die Standardabweichung der Mittelwerte unserer Stichprobe ist also:
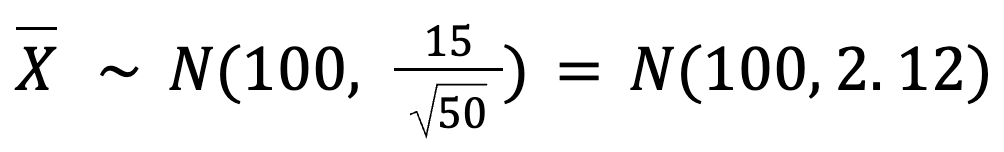
Das sagt uns, dass die Mittelwerte der Stichprobe sehr nahe an 100 Tassen liegen und nur eine kleine Abweichung (etwa 2,12 Tassen) aufweisen werden.
Warum der zentrale Grenzwertsatz wichtig ist
Wir wissen jetzt, dass Daten in der realen Welt seltsam und unberechenbar sein können. Aber der zentrale Grenzwertsatz gibt uns einen zuverlässigen Weg, um zu verstehen, was vor sich geht, und auf dieser Grundlage bessere Entscheidungen zu treffen. Wir wollen seine Bedeutung genauer verstehen.
Statistische Schlussfolgerungen
In der Statistik ist der zentrale Grenzwertsatz der Grund, warum parametrische Tests wie t-Tests, ANOVA und Regression so funktionieren, wie sie funktionieren. Diese Tests beruhen auf der Vorstellung, dass die Stichprobendaten aus einer Grundgesamtheit mit festen Merkmalen stammen.
Ohne den zentralen Grenzwertsatz könnten wir uns nicht auf diese Tests verlassen. Aufgrund dieses Theorems sind parametrische Tests oft aussagekräftiger als nicht-parametrische Tests, die keine Annahmen über die Verteilung der Daten machen.
Anwendungen in der Industrie
Sie taucht auch in vielen realen Situationen auf. In der Finanzwelt verwenden Analysten sie, um die durchschnittlichen Aktienrenditen auf der Grundlage der vergangenen Performance zu schätzen. Bei Umfragen und Erhebungen werden anhand einer Stichprobe von Antworten Vorhersagen über die gesamte Bevölkerung getroffen. Beim maschinellen Lernen und bei Big Data verwenden wir sie, wenn Modelle auf Stichproben trainiert werden. Eine Film-App kann zum Beispiel eine Stichprobe von Nutzeraktivitäten nutzen, um ihr Empfehlungssystem aufzubauen.
Rechner für den zentralen Grenzwertsatz
Die Standardabweichung ist eine Zahl, die uns sagt, wie weit die Werte vom Durchschnitt entfernt sind. Wenn wir uns die Mittelwerte von Stichproben (die Durchschnittswerte verschiedener Stichproben) ansehen, wollen wir wissen, wie stark diese Durchschnittswerte variieren. Dafür können wir diese Formel verwenden:
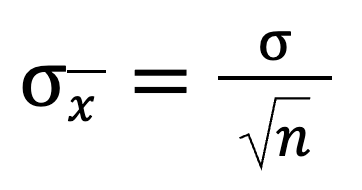
Wenn wir also die Standardabweichung der Grundgesamtheit durch die Quadratwurzel aus dem Stichprobenumfang teilen, erhalten wir die Standardabweichung der Stichprobenverteilung. Je größer die Stichprobe ist, desto kleiner wird der Gesamtwert.
Schauen wir uns ein kurzes Beispiel an:
| Stichprobengröße (n) | Stichprobenmittelwert (μₓ̄) | Std. Abweichung (σₓ̄) |
|---|---|---|
| 5 | 17 | 1.788854 |
| 10 | 17 | 1.264911 |
| 25 | 17 | 0.800000 |
| 50 | 17 | 0.565685 |
| 100 | 17 | 0.400000 |
Du kannst sehen, dass der Mittelwert gleich bleibt, aber die Standardabweichung immer kleiner wird. Das zeigt: Je größer die Stichprobe ist, desto genauer und konsistenter ist sie.
Der zentrale Grenzwertsatz in der Datenwissenschaft
In der Datenwissenschaft beschäftigen wir uns normalerweise mit Stichproben, nicht mit ganzen Populationen. Die CLT hilft uns zu verstehen, wie sich diese Stichprobenergebnisse verhalten, und sie sagt uns, dass, wenn wir genügend Stichproben nehmen, ihre Mittelwerte anfangen, wie eine Normalverteilung auszusehen, auch wenn die ursprünglichen Daten alles andere als das sind.
Das hat auch in der realen Welt einige große Vorteile. Beim maschinellen Lernen verwenden wir oft Techniken wie Bootstrapping, um Werte zu schätzen. Dank des CLT können wir sicher sein, dass diese Schätzungen korrekt sind.
Sie ist auch ein wichtiger Akteur bei A/B-Tests. Wenn ein Unternehmen zwei Versionen einer Webseite oder eines Features ausprobiert, hilft uns der CLT dabei herauszufinden, ob die Ergebnisse aussagekräftig sind oder zufälliges Rauschen.
Selbst beim Verstärkungslernen, bei dem Systeme durch Versuch und Irrtum lernen, bügelt die CLT das Chaos aus. Je mehr Daten reinkommen, desto stabiler werden die Durchschnittswerte, wodurch das System schneller und besser lernt.
Schließlich wirst du die CLT auch bei Hypothesentests und Zeitreihenanalysen entdecken. Es hilft Datenwissenschaftlern, Ideen zu testen und Trends mit größerer Sicherheit zu verfolgen.
Schlussgedanken
Der zentrale Grenzwertsatz mag technisch klingen, wenn du neu in der Statistik bist, aber er ist ein wichtiger Grund dafür, dass wir intelligente Dinge mit Daten machen können. Sie verwandelt den Zufall in etwas, das wir verstehen und dem wir vertrauen können. Sie ist sogar einer der Bausteine der statistischen Modellierung und ein Muss für jeden, der mit Daten arbeitet.
Wenn du mehr wissen willst, lies das Gesetz der großen Zahlen und die Wahrscheinlichkeitsverteilungen - sie hängen alle zusammen.
Ich bin ein Inhaltsstratege, der es liebt, komplexe Themen zu vereinfachen. Ich habe Unternehmen wie Splunk, Hackernoon und Tiiny Host geholfen, ansprechende und informative Inhalte für ihr Publikum zu erstellen.
FAQs zum zentralen Grenzwertsatz
Kann der zentrale Grenzwertsatz auch auf nicht-numerische Daten angewendet werden?
Ja, aber nicht direkt. Die CLT gilt für numerische Daten, insbesondere für Mittelwerte und Summen. Bei kategorialen oder ordinalen Daten kannst du jedoch ähnliche Prinzipien anwenden, indem du die Daten in eine numerische Form umwandelst oder andere statistische Verfahren einsetzt.
Was ist der Unterschied zwischen einer Stichprobenverteilung und einer Bevölkerungsverteilung?
Die Bevölkerungsverteilung beschreibt den gesamten Datensatz, während sich die Stichprobenverteilung auf die Verteilung von Stichprobenstatistiken (wie Mittelwerte) aus wiederholten Stichproben bezieht.
Wie wirken sich Ausreißer auf den zentralen Grenzwertsatz aus?
Ausreißer erhöhen die Schiefe und die Varianz, was bedeutet, dass wir möglicherweise einen größeren Stichprobenumfang benötigen, damit sich die Stichprobenverteilung der Normalität annähert.

