Gesetz der großen Zahlen: Ein Schlüssel zum Verständnis von Unsicherheit

Ein Ergebnis allein sagt noch nicht viel aus. Angenommen, du wirfst einmal eine Münze und bekommst Kopf. Das beweist gar nichts - es könnte auch zufällig so gelandet sein. Aber wenn du die Münze 100 Mal wirfst, wirst du sehen, dass Kopf und Zahl in etwa gleich oft vorkommen. Dann beginnt der Durchschnitt Sinn zu machen.

Und genau darum geht es beim Gesetz der großen Zahlen. Je mehr Daten du sammelst, desto genauer wird dein Durchschnitt. Es hilft dir, das große Ganze zu sehen.

In diesem Leitfaden erklären wir dir, was das Gesetz der großen Zahlen bedeutet, wie es im echten Leben funktioniert und warum es so hilfreich ist, wenn du versuchst, Muster zu verstehen oder bessere Entscheidungen im Laufe der Zeit zu treffen.

Was ist das Gesetz der großen Zahlen?

DasGesetz der großen Zahlen ist ein Prinzip aus der Wahrscheinlichkeitsrechnung und Statistik, das erklärt, wie sich dieerages verhalten, wenn mehr Daten gesammelt werden. Je größer deine Stichprobe ist, desto näher kommt der Durchschnitt der Stichprobe ( Stichprobenmittelwert) dem wahren Durchschnitt der gesamten Gruppe ( Populationsmittelwert).

In der realen Welt haben wir normalerweise keinen Zugang zu den Daten einer ganzen Bevölkerung. Stattdessen nehmen wir eine Stichprobe, wie die Befragung von 1.000 Wählern, statt aller 300 Millionen Menschen. Das Gesetz der großen Zahlen gibt uns die Gewissheit, dass der Stichprobendurchschnitt bei genügend Daten nahe an der Realität liegt.

Je größer die Stichprobe wird, desto mehr heben sich die zufälligen Schwankungen auf. Ausreißer haben weniger Einfluss, und der Durchschnitt wird stabiler und berechenbarer.

Es gibt zwei Hauptversionen des Gesetzes, und sie unterscheiden sich darin, wie stark sie diese Wirkung garantieren:

Schwaches Gesetz (Konvergenz der Wahrscheinlichkeiten)

Das schwache Gesetz der großen Zahlen besagt, dass sich der Mittelwert der Stichprobe wahrscheinlich dem Mittelwert der Grundgesamtheit annähert, wenn die Stichprobe größer wird. Je mehr Daten du sammelst, desto unwahrscheinlicher ist es, dass dein Durchschnitt weit daneben liegt.

Du wirfst zum Beispiel eine faire Münze. Je öfter du schnippst, desto mehr nähert sich das Verhältnis von Kopf zu Zahl dem Verhältnis 50/50. Es landet vielleicht nicht perfekt, aber es kommt dem ziemlich nahe, und genau darum geht es bei dem schwachen Gesetz.

Starkes Gesetz (fast sichere Konvergenz)

Das starke Gesetz der großen Zahlen geht noch einen Schritt weiter. Sie besagt, dass der Mittelwert der Stichprobe sich dem Mittelwert der Grundgesamtheit annähert und mit ziemlicher Sicherheit dort bleibt, nicht nur wahrscheinlich.

Einfach ausgedrückt: Wenn du die Münze immer wieder wirfst, wird das Verhältnis von Kopf zu Zahl nicht annähernd 50:50 betragen, sondern sich dort einpendeln. Dieses Gesetz gibt uns also die nahezu absolute Gewissheit, dass die langfristigen Durchschnittswerte die Wahrheit widerspiegeln, mit nur wenigen Ausnahmen.

Reale Beispiele für das Gesetz bei der Arbeit

Schauen wir uns ein paar Beispiele aus der Praxis an, um zu verstehen, wie dieses Gesetz funktioniert:

Münzwürfe oder Würfelwürfe

Stell dir vor, du würfelst dreimal mit einem normalen sechsseitigen Würfel. Du kannst Ergebnisse wie 6, 2 und 5 erhalten. Der Durchschnitt liegt bei 4,3 und damit höher als der erwartete Wert von 3,5. Aber jetzt würfelst du erst 100 Mal, dann 1.000 Mal. Je mehr Würfe du machst, desto näher kommt dein Durchschnitt an 3,5. Das Gesetz der großen Zahlen glättet die Zufälligkeiten im Laufe der Zeit.

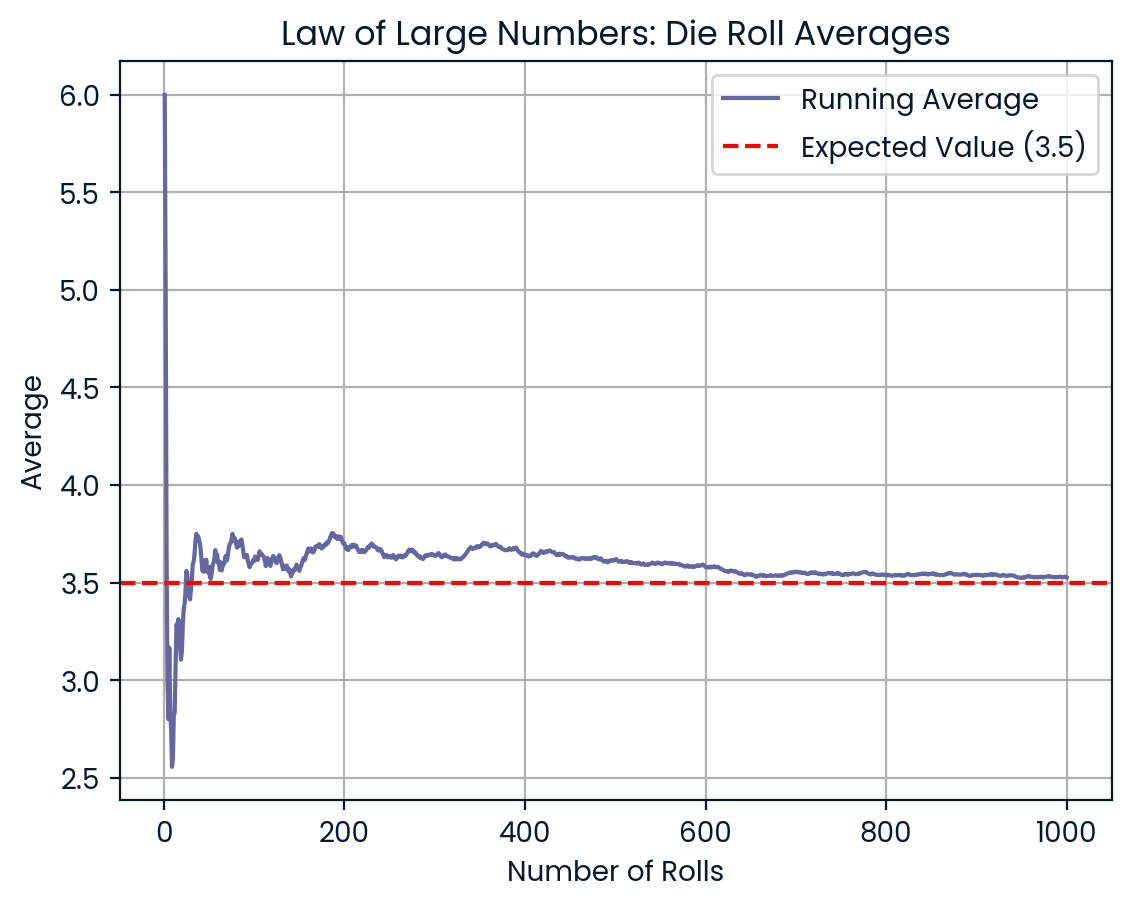
Mehr Würfe lassen den Durchschnitt näher an 3,5 herankommen. Bild vom Autor.

Sportstatistiken

Sportler können gute und schlechte Tage haben. Ein Quarterback kann in einem Spiel 9 von 10 Pässen anbringen, das sind beeindruckende 90 %. Das heißt aber nicht, dass sie immer auf diesem Niveau spielen.

Über eine ganze Saison hinweg, mit hunderten von Würfen, beginnt sich die Abschlussquote einzupendeln. Diese Saisonstatistik gibt einen viel besseren Eindruck von den tatsächlichen Fähigkeiten des Spielers.

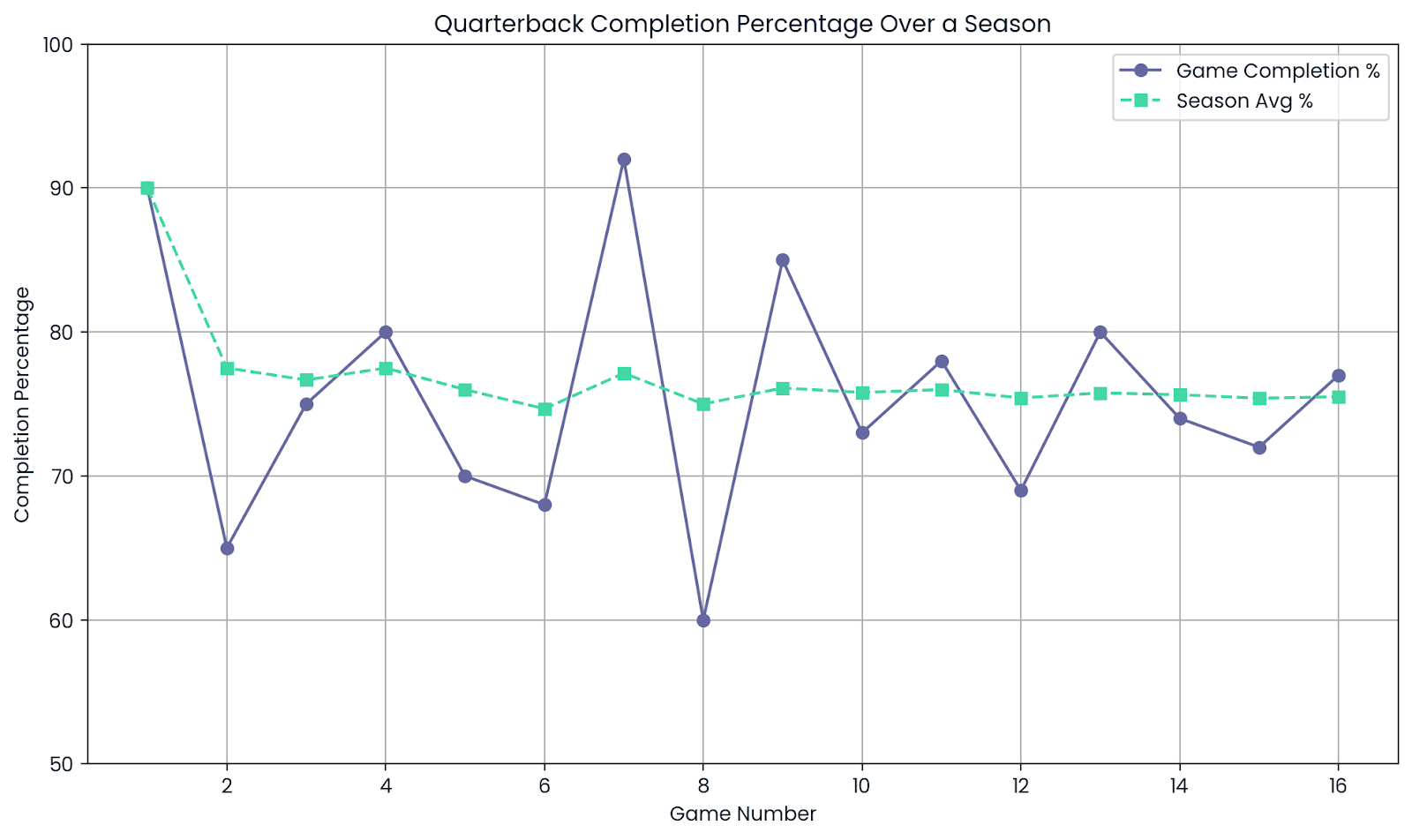
Durchschnittlich. Bild vom Autor.

Risikopooling in der Versicherungsbranche 

Die Versicherungsgesellschaften wissen nicht genau, wie viel eine Person sie kosten wird. Manche Menschen nehmen überhaupt keine medizinische Versorgung in Anspruch, andere schon.

Aber wenn du dir eine große Gruppe von Menschen ansiehst, gleichen sich diese Höhen und Tiefen aus. Indem sie das Risiko auf Tausende von Versicherungsnehmern verteilen, können die Versicherer die durchschnittlichen Kosten genauer vorhersagen.

So können sie faire Preise (Prämien) festlegen und gleichzeitig finanziell stabil bleiben.

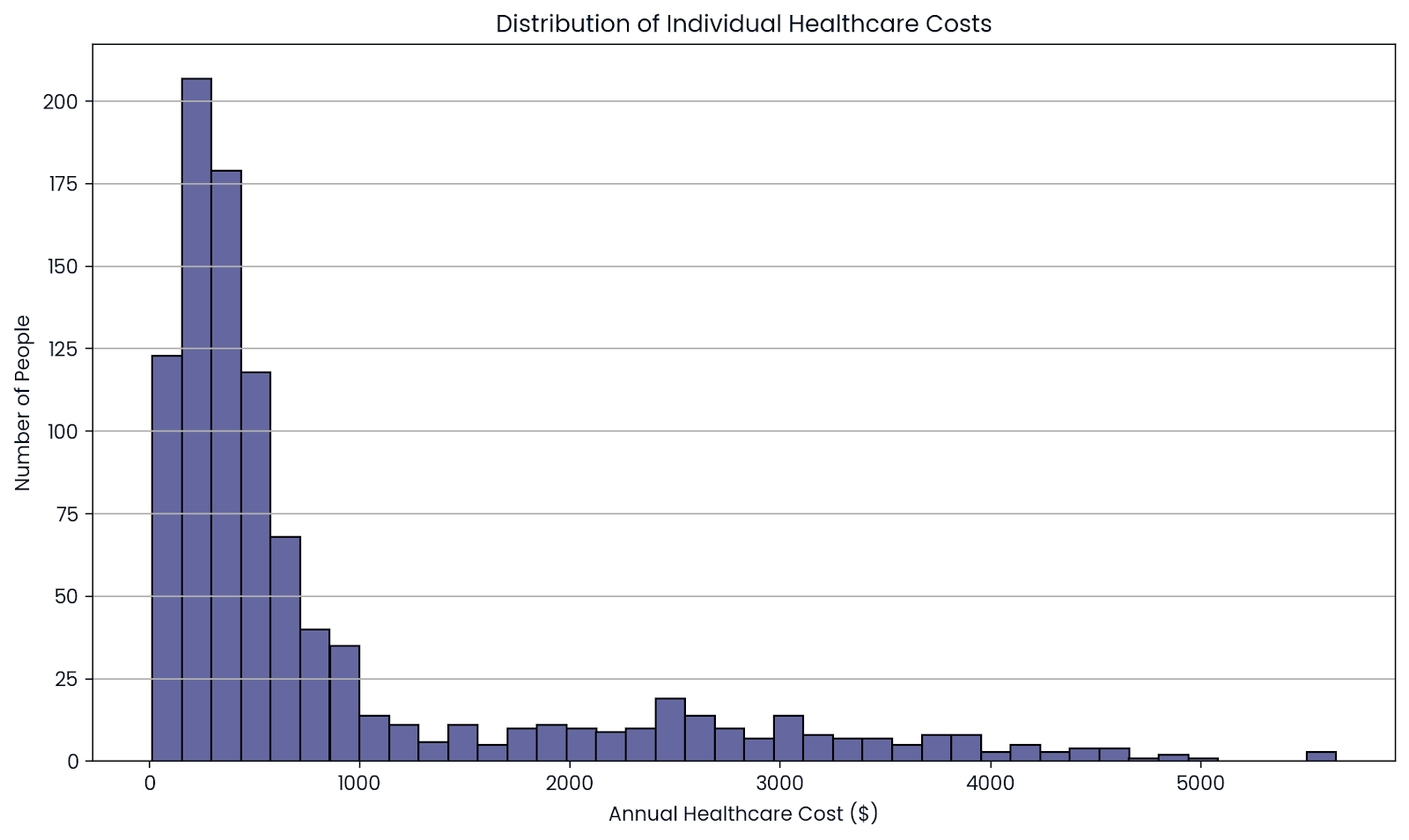
Der Durchschnitt über viele Menschen zeigt die wahren Kosten. Bild vom Autor.

Casinospiele und Hausvorteil

Casinos bauen in jedem Spiel einen leichten Vorteil auf. Wenn du Blackjack spielst, kannst du fünf Hände hintereinander gewinnen oder zehn verlieren. Aber bei tausenden von Spielen ist das durchschnittliche Ergebnis zugunsten des Casinos.

Wenn der Hausvorteil zum Beispiel 0,5 % beträgt, dann erwartet das Casino im Laufe der Zeit, dass es im Durchschnitt 50 Cent pro 100 Dollar Einsatz verdient. Das passiert vielleicht nicht in einer kurzen Sitzung, aber über Millionen von Spielen summiert es sich genau wie erwartet.

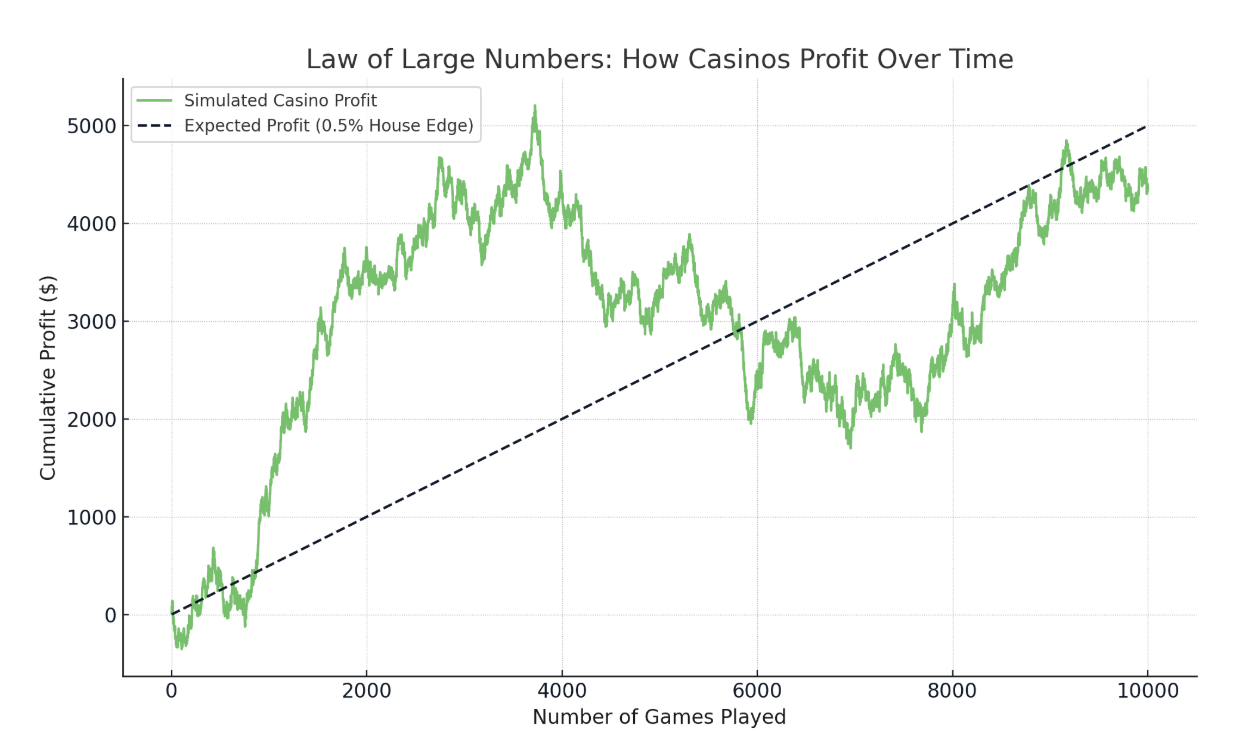
Der Vorteil des Casinos gewinnt mit mehr Einsätzen. Bild vom Autor.

A/B-Tests in Tech-Unternehmen

Angenommen, ein Unternehmen möchte zwei Versionen eines Website-Buttons testen: Button A und Button B. Nachdem 20 Leute beide ausprobiert haben, sieht Button A besser aus. Aber das sind nicht genug Daten, um dem Ergebnis zu vertrauen.

Jetzt lass 20.000 Nutzer beides sehen. Je größer die Stichprobe wird, desto zuverlässiger werden die durchschnittlichen Klickraten und desto klarer wird, welcher Button am besten abschneidet.

Deshalb setzen Unternehmen bei A/B-Tests auf große Stichproben. Das Gesetz der großen Zahlen hilft ihnen, Fehlalarme zu vermeiden und klügere Entscheidungen zu treffen.

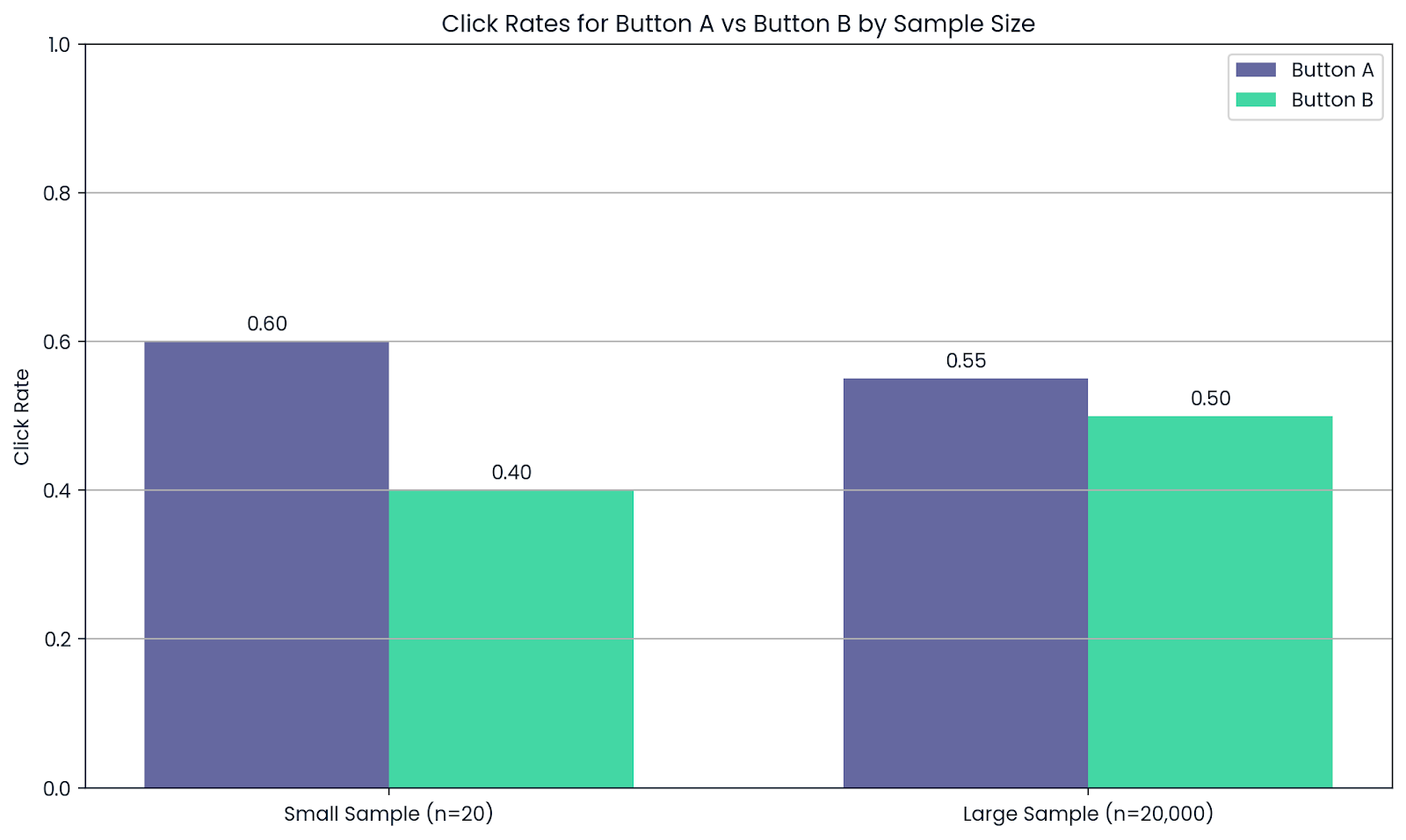
Je mehr Menschen getestet werden, desto zuverlässiger sind die Ergebnisse. Bild vom Autor.

Warum das Gesetz der großen Zahlen wichtig ist

In der Datenwissenschaft verwenden wir oft Daten, um Modelle zu trainieren. Aber wenn der Datensatz zu klein ist, können ein paar ungewöhnliche Werte die Ergebnisse verfälschen.

Du testest zum Beispiel einen neuen Empfehlungsalgorithmus mit nur 10 Nutzern. Wenn ein/e Nutzer/in alles anklickt und ein/e andere/r nichts, kann deine durchschnittliche Leistung gut oder schlecht aussehen. Das bedeutet nicht, dass das Modell gut oder schlecht ist; es bedeutet, dass deine Stichprobe zu klein ist, um ihr zu vertrauen.

Das Gesetz der großen Zahlen besagt, dass sich zufällige Schwankungen ausgleichen, je mehr Daten wir sammeln, und dass das Durchschnittsergebnis zuverlässiger wird. Deshalb liefern große Datensätze bessere Vorhersagen und Erkenntnisse.

Du siehst das auch in Simulationen. Nimm zum Beispiel die Monte-Carlo-Methode. Dabei wird das gleiche Szenario tausende Male mit zufälligen Eingaben durchgespielt. Das Gesetz der großen Zahlen garantiert, dass das durchschnittliche Ergebnis umso näher am erwarteten Ergebnis liegt, je mehr Versuche wir durchführen.

Beim maschinellen Lernen zeigt sich das Gesetz auf zwei wichtige Arten:

• Modellschulung: Ein Modell, das auf einem kleinen, unausgewogenen Datensatz trainiert wurde, lernt möglicherweise Muster, die die reale Welt nicht widerspiegeln. Aber mit genügend unterschiedlichen Daten lernt das Modell, was tatsächlich funktioniert.
• Modellversuche: Wenn du ein Modell mit nur 50 Nutzern testest, kann das ganz andere Ergebnisse bringen als wenn du es mit 5.000 Nutzern testest. Ein größerer Testsatz vermittelt ein klareres Bild davon, wie das Modell abschneiden wird, sobald es eingesetzt wird.

Kurz gesagt: Mehr Daten bedeuten weniger Lärm und bessere Entscheidungen. 

Häufige Missverständnisse

Das Gesetz der großen Zahlen wird oft missverstanden, wenn die Leute erwarten, dass es sofort funktioniert.

Wenn du glaubst, dass sich die Ergebnisse schnell "ausgleichen" werden, ist das ein Fehler. Wenn du zum Beispiel eine Münze wirfst und fünfmal hintereinander Kopf bekommst, könntest du denken, dass jetzt die Zahl "fällig" ist, um die Dinge auszugleichen. Aber so funktioniert die Wahrscheinlichkeitsrechnung nicht.

Diese Denkweise ist als Spielertäuschung bekannt: die falsche Vorstellung, dass vergangene Ergebnisse zukünftige Ergebnisse in einem echten Zufallsprozess beeinflussen. In Wirklichkeit ist jeder Münzwurf immer noch eine 50/50 Chance, egal was vorher passiert ist.

Das Gesetz der großen Zahlen verspricht nicht, dass sich der Zufall auf kurze Sicht glättet. Stattdessen sagt sie uns, dass sich das durchschnittliche Ergebnis über viele, viele Versuche hinweg dem erwarteten Wert nähert. Bei einer fairen Münze bedeutet das, dass sie irgendwann zur Hälfte Kopf und zur Hälfte Zahl ist, nicht sofort.

Kurze Ausreißer oder ungewöhnliche Muster können trotzdem vorkommen. So sieht der Zufall eben in kleinen Stichproben aus. Das Gesetz wird erst dann sinnvoll, wenn du herauszoomst und das große Ganze betrachtest.

Wie es mit anderen Konzepten zusammenhängt

Während das Gesetz der großen Zahlen besagt, dass sich der Stichprobendurchschnitt mit zunehmender Stichprobengröße dem wahren Durchschnitt annähert, geht der zentrale Grenzwertsatz (CLT ) noch weiter. Sie erklärt, wie die Verteilung dieser Durchschnittswerte aussieht.

Wenn du viele große Stichproben nimmst und ihre Mittelwerte berechnest, bilden diese Mittelwerte eine glockenförmige Kurve (eine Normalverteilung), egal wie die ursprünglichen Daten aussahen, so die CLT. 

Beide sind in der Statistik wichtig, aber sie beschreiben unterschiedliche Dinge: Das eine konzentriert sich auf die Genauigkeit, das andere auf die Form.

Die wichtigsten Erkenntnisse

Das Gesetz der großen Zahlen verdeutlicht ein zentrales Prinzip der Datenanalyse: Größere Stichproben führen zu stabileren und genaueren Ergebnissen, aber nur, wenn die Daten repräsentativ sind. 

Obwohl große Datensätze die Auswirkungen zufälliger Schwankungen verringern, sind mehr Daten nicht immer besser. Wenn die Daten verzerrt oder unausgewogen sind, kann selbst ein umfangreicher Datensatz zu irreführenden Ergebnissen führen. Um gültige Schlussfolgerungen zu ziehen, brauchst du sowohl Umfang als auch Qualität.

Wenn du dir eine solidere Grundlage für diese Konzepte aneignen möchtest, ist der Kurs Statistisches Denken in Python ein guter Anfang. Danach erkundest du die Gauß-Verteilung, um zu verstehen, wie das Gesetz der großen Zahlen mit anderen wichtigen Werkzeugen der Statistik und des maschinellen Lernens zusammenhängt.