He probado DeepSeek R1 Lite Preview para ver si es mejor que O1

¿Qué es DeepSeek-R1-Lite-Preview?

DeepSeek-R1-Lite-Preview es una herramienta de IA, similar a ChatGPTcreada por la empresa china DeepSeek. La empresa anunció este nuevo modelo en X el 20 de noviembre (enlace tuit) y compartió algunos detalles en una página de documentación.

DeepSeek-R1-Lite-Preview está pensado para ser realmente bueno resolviendo problemas complejos de razonamiento en matemáticas, codificación y lógica. Te muestra cómo piensa paso a paso para que puedas entender cómo llega a las respuestas, lo que ayuda a que la gente confíe más en él.

Puedes probarlo gratis en su sitio web, chat.deepseek.compero estás limitado a 50 mensajes al día en su modo avanzado llamado "Deep Think". DeepSeek también tiene previsto compartir partes de esta herramienta con el público para que otros puedan utilizarla o basarse en ella.

Cómo utilizar DeepSeek-R1-Lite-Preview

Puedes empezar a utilizar DeepSeek-R1-Lite-Preview siguiendo estos dos pasos:

1. Visita la página de chat de DeepSeek y conéctate.
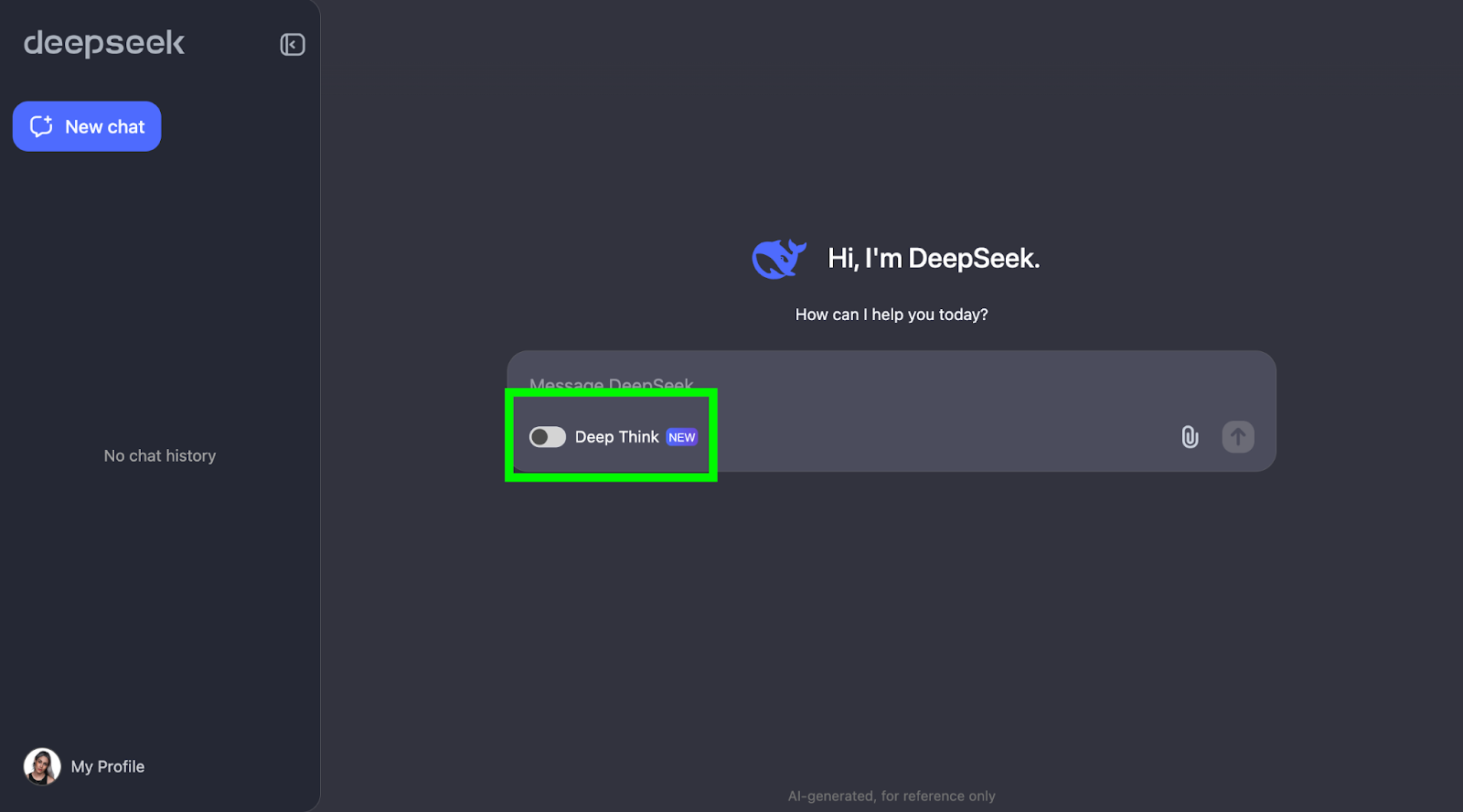
2. Activa el "Pensamiento Profundo".

La prueba de la fresa

Para ver lo que puede hacer DeepSeek-R1-Lite-Preview, ¡pongámoslo a prueba! Te propongo una serie de retos que demuestran su capacidad de razonamiento, empezando por la sencilla pero famosa pregunta de la fresa: ¿Cuántas veces aparece la letra "r" en "fresa"?"

Esta pregunta puede parecer sencilla, pero los LLM (incluso los GPT-4o) han tenido tradicionalmente dificultades para responderla correctamente: suelen contestar que sólo hay dos apariciones de la letra"r".

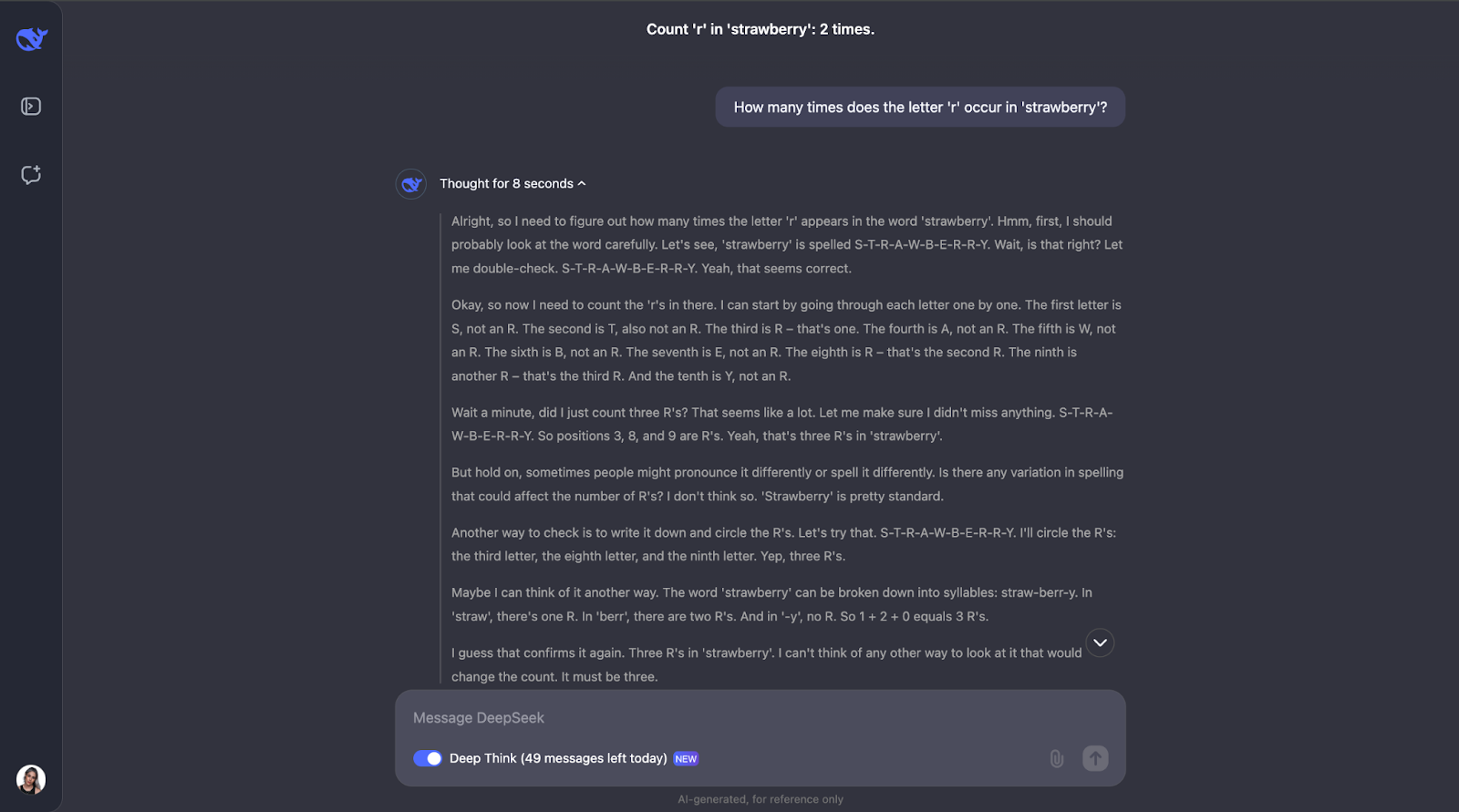
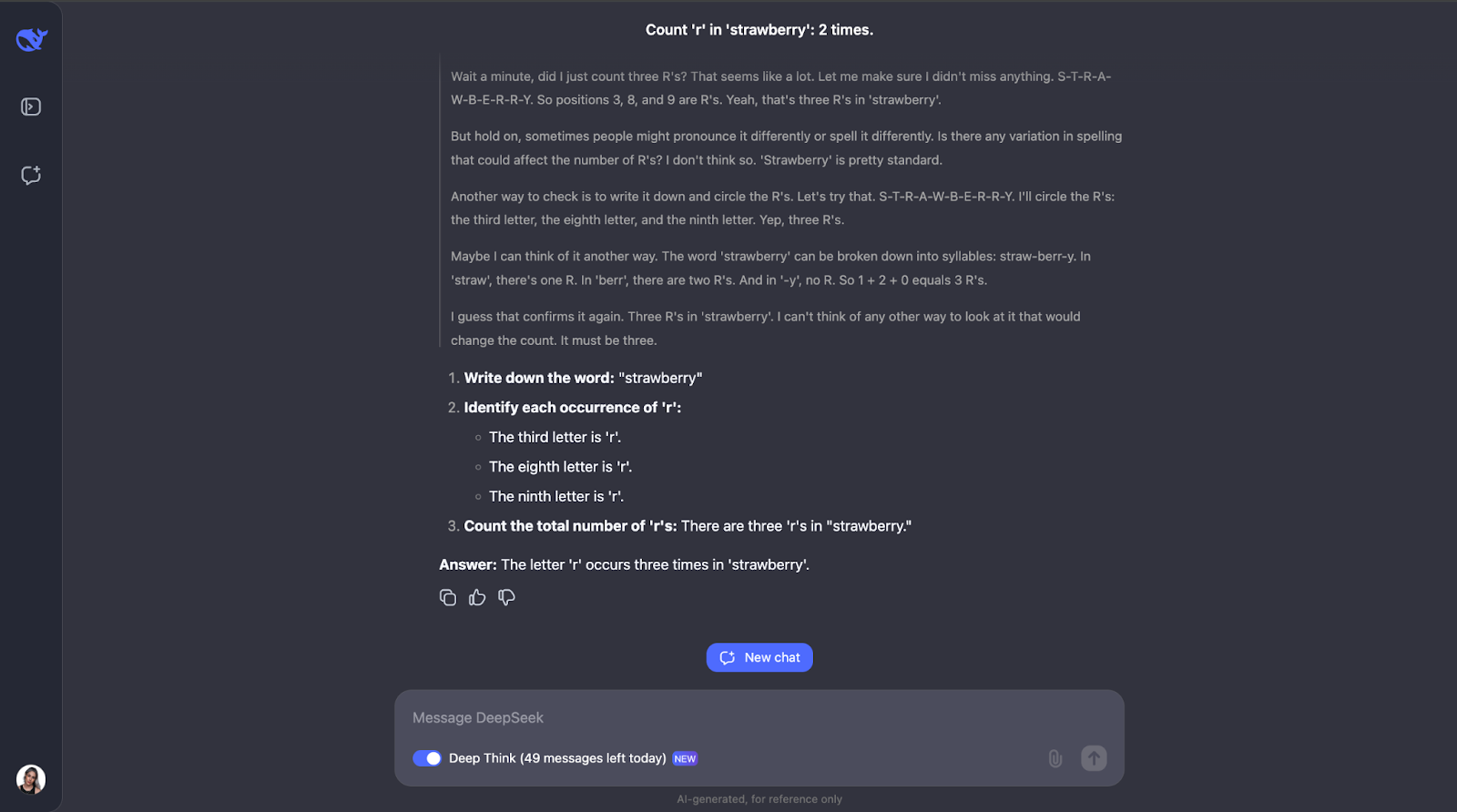
Vaya, vale, no esperaba un proceso de razonamiento tan largo para lo que parece una tarea sencilla. Pensaba que después de contar la letra "r" e identificar su posición en la palabra, se habría detenido ahí. Pero lo que me parece interesante es que no se detuvo ahí. Comprobó el recuento un par de veces e incluso tuvo en cuenta cosas como que la gente podría pronunciar o deletrear la palabra de forma diferente, lo que me parece un poco redundante, sobre todo la parte de la pronunciación. ¡Pero eso demuestra lo cuidadoso y reflexivo que es! También explicaba cada paso para que pudiera seguir su proceso de pensamiento y ver cómo llegaba a la respuesta.

Razonamiento matemático

Probaré DeepSeek-R1-Lite-Preview en tres problemas de matemáticas.

Zona triangular

Dadas las pretensiones de DeepSeek de ser realmente bueno en razonamiento matemático, empecemos con un sencillo problema geométrico.

"Si un triángulo tiene lados de longitud 3, 4 y 5, ¿cuál es su área?"

Este problema requiere conocer el teorema de Pitágoras y la fórmula de Herón. Yo esperaría que DeepSeek-R1-Lite-Preview mostrara su trabajo, tal vez así:

• Reconócelo como un triángulo rectángulo 3-4-5
• Calcula el semiperímetro: s = (3 + 4 + 5) / 2 = 6
• Aplica la fórmula de Heron: Área = √(s(s-a)(s-b)(s-c))
• Sustituye los valores: Area = √(6(6-3)(6-4)(6-5)) = √(6 * 3 * 2 * 1) = √36 = 6
• Verifícalo: Área del triángulo rectángulo = (base * altura) / 2 = (3 * 4) / 2 = 6

¡A ver qué pasa!

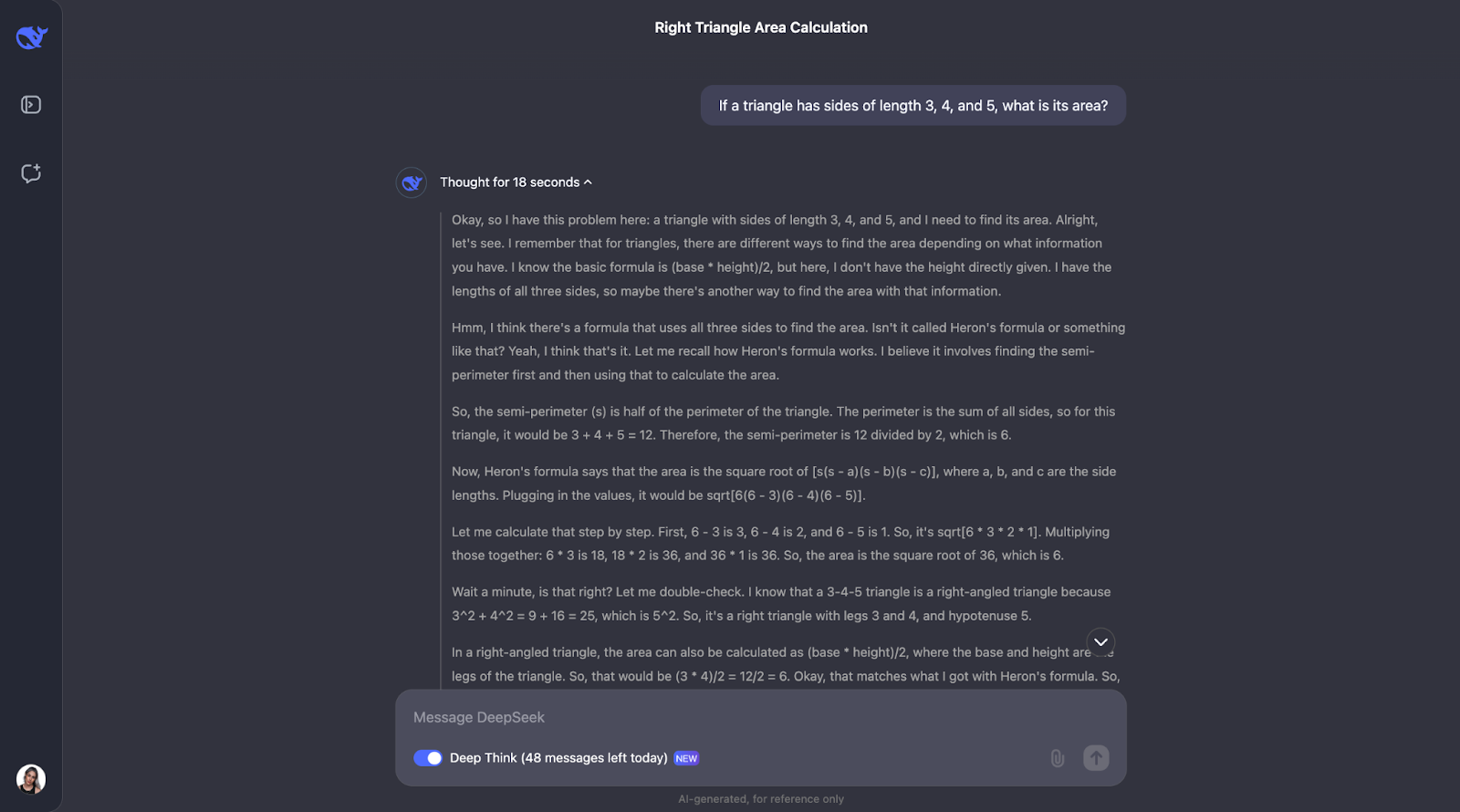
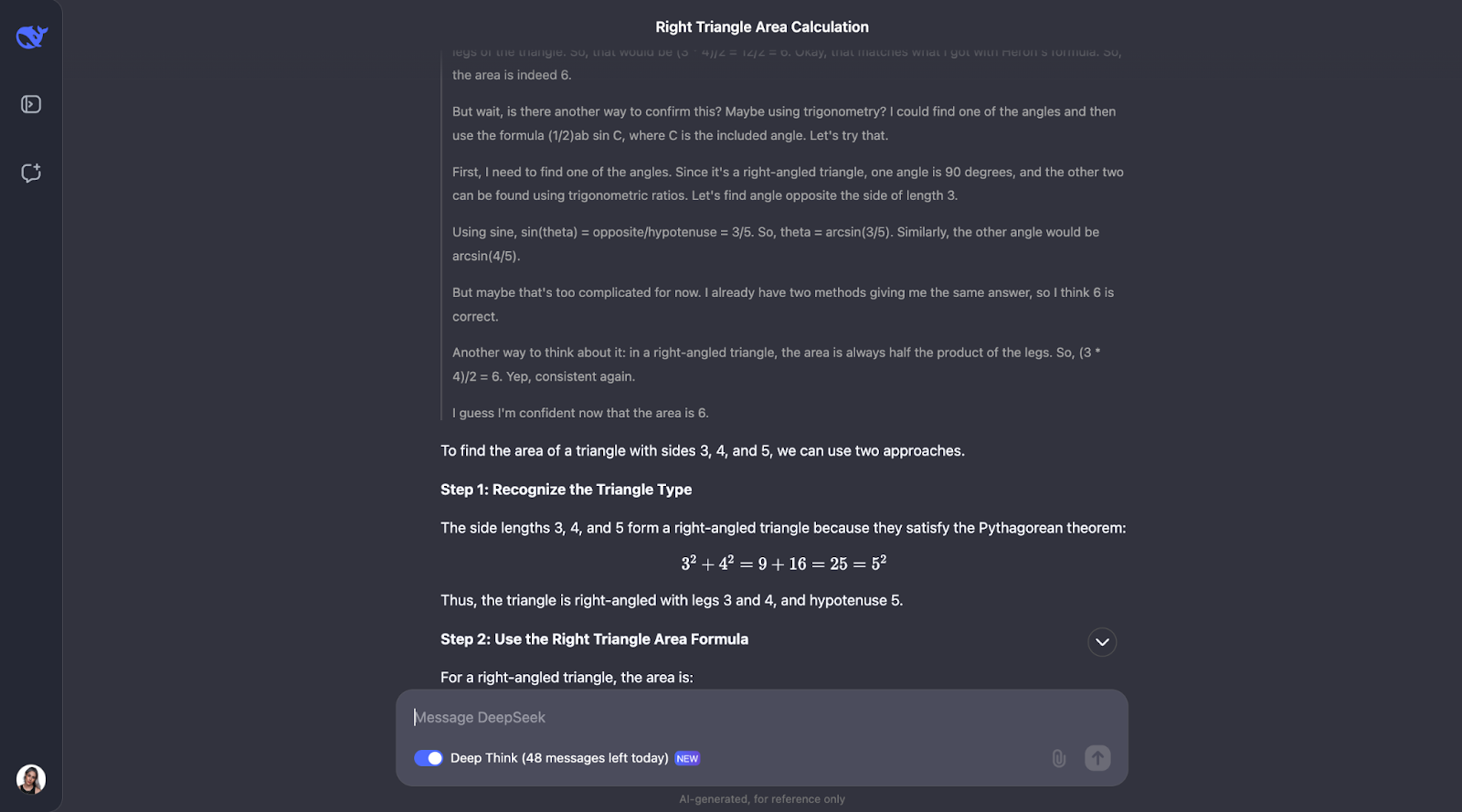
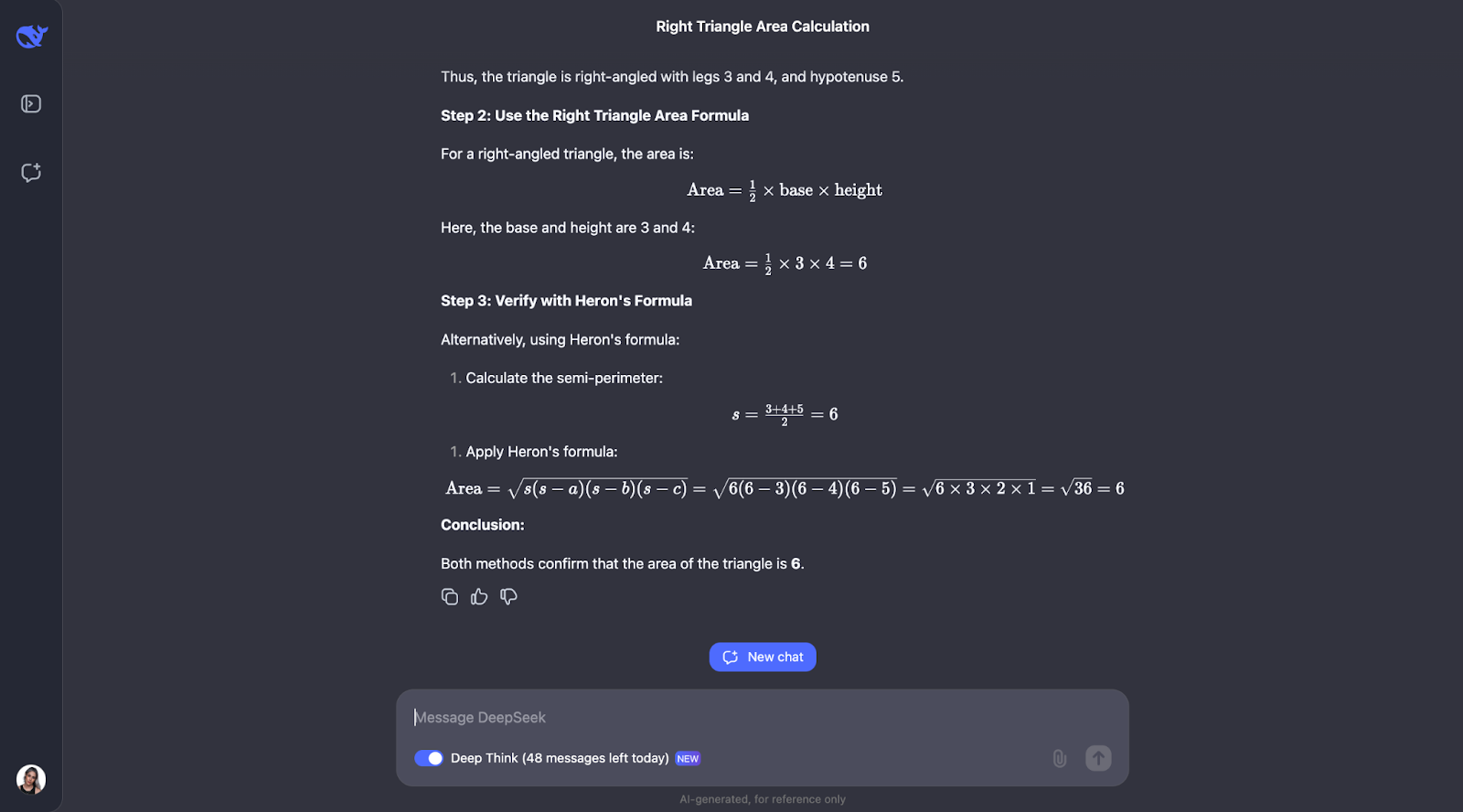
Okay, pues curiosamente, realiza las comprobaciones que predije, aunque en un orden diferente. También se planteó utilizar la trigonometría calculando ángulos y probando otra fórmula. Me parece muy interesante que, al final, decidiera que no era necesario, puesto que los dos primeros métodos ya habían confirmado la respuesta.

Tanto la explicación como el resultado fueron especialmente claros y fáciles de seguir, lo que me hace pensar que éste sería un modelo fantástico para integrar en el ayudante de un alumno de matemáticas, por ejemplo. Para este caso de uso concreto, quizá podría mostrarse primero el proceso de pensamiento, y el alumno podría interactuar con él, reconociendo si lo ha entendido o no antes de pasar a la respuesta final.

Prueba matemática

Pasemos a una prueba matemática más compleja para ver si hay alguna diferencia en el rendimiento y el proceso de pensamiento.

"Demuestra que la suma de los recíprocos de los números de Fibonacci converge a un valor finito".

Esta prueba pone a prueba la comprensión del modelo de conceptos matemáticos avanzados, como la convergencia de series y las propiedades de los números de Fibonacci. ¡Vamos a probarlo! En aras de la legibilidad, sólo publicaré la primera y la última parte de la respuesta (pero no dudes en intentarlo tú mismo con el mismo prompt):

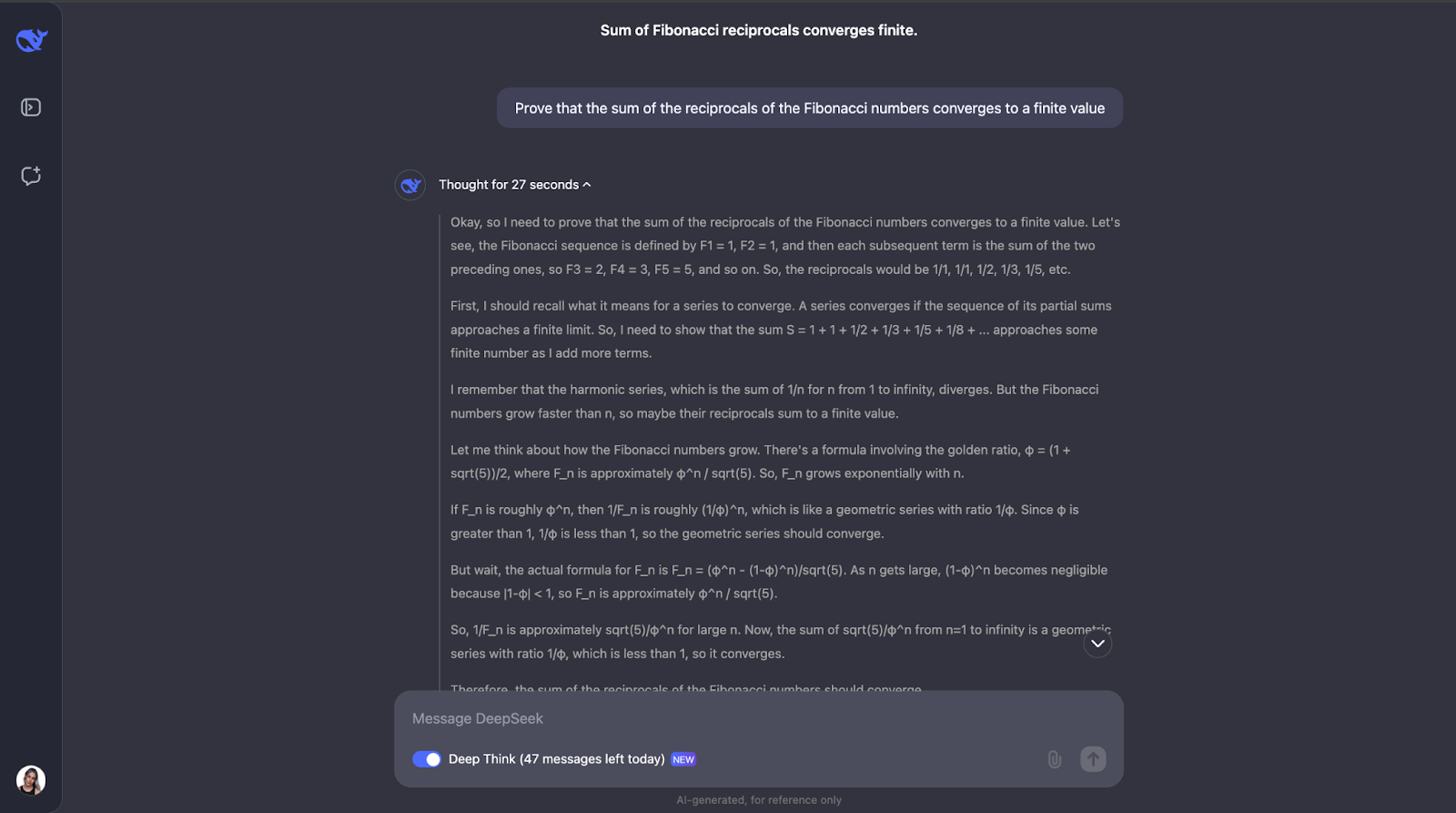
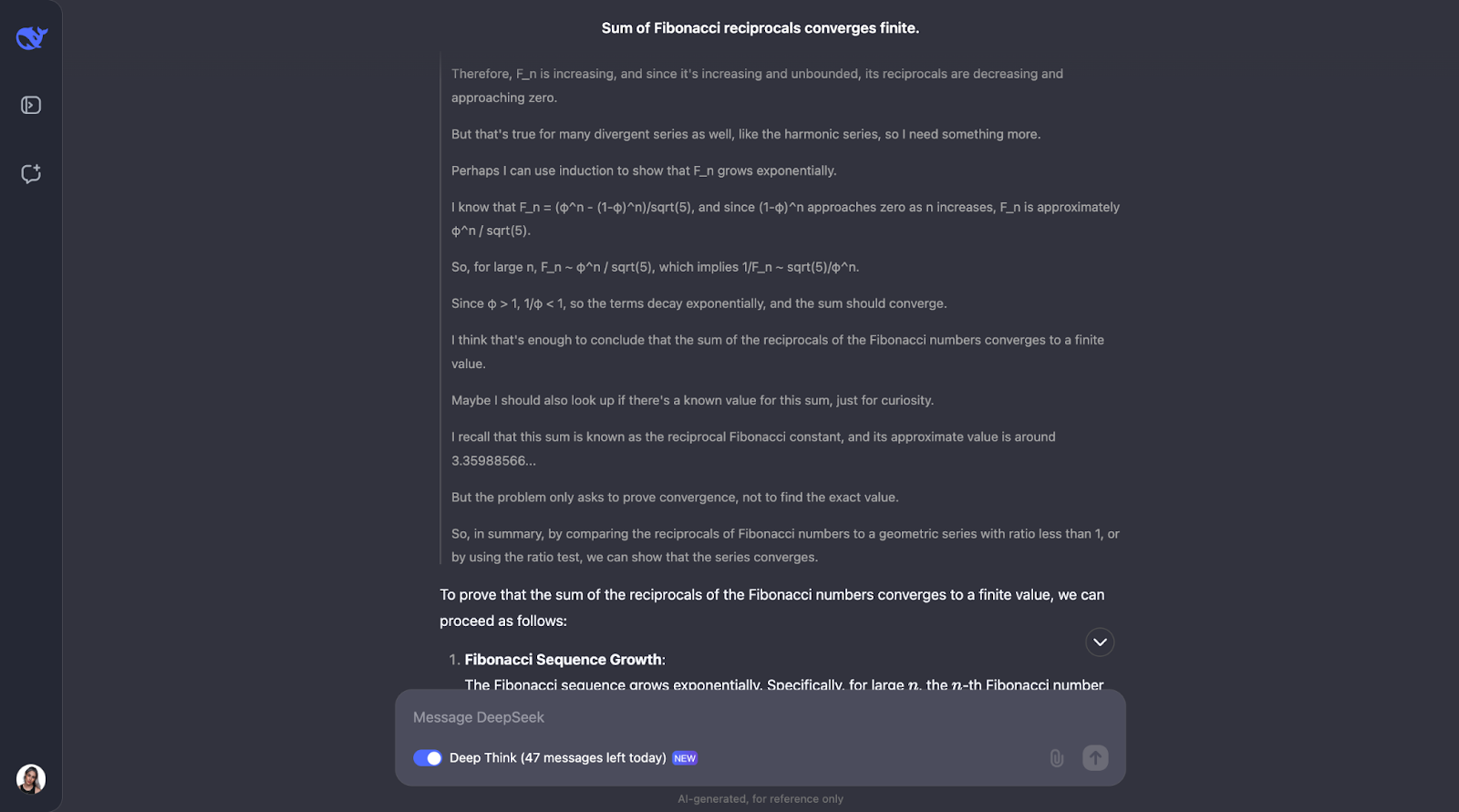
Vale, así que éste es un gran tren de pensamiento; me gusta mucho cómo se asegura primero de que comprende los conceptos clave, como los recíprocos y la convergencia. Entonces, DeepSeek-R1-Lite-Preview abordó este problema observando cómo crecen los números de Fibonacci y utilizando una prueba de comparación, que es una forma habitual de comprobar si una serie converge o no.

Comparaba los recíprocos de los números de Fibonacci con una serie geométrica. Como los recíprocos de los números de Fibonacci disminuyen aún más rápido que una serie geométrica con un cociente común inferior a 1, el modelo concluyó que la suma de los recíprocos también converge a un valor finito. Para mayor seguridad, utilizó algo llamado prueba de la proporción.

Esta prueba comprueba si el límite de la relación de términos consecutivos es menor que 1. Si lo es, la serie converge. El modelo calculó este cociente para los recíprocos de los números de Fibonacci y descubrió que, efectivamente, es inferior a 1.

Incluso mencionaba que existe un valor conocido para esta suma llamado constante recíproca de Fibonacci, que es aproximadamente 3,3598. Pero para este problema, sólo necesitábamos saber que la suma es finita, no lo que es exactamente, así que ésta era una información extra que también me pareció interesante. Me gusta mucho cómo se presenta la solución en la salida. Es claro y paso a paso. 

Hasta ahora, estoy impresionado con las tareas matemáticas.

Geometría diferencial

Voy a intentar un problema de geometría diferencial, sólo porque mi doctorado es en este campo, así que no he podido resistirme a hacer una pequeña prueba. Nada demasiado complejo, sólo un ejercicio clásico que puedes encontrar en matemáticas de pregrado.

"Considera una superficie S en R³ parametrizada por

φ(u,v) = (u cos v, u sen v, ln u)

para u > 0 y 0 ≤ v < 2π.

a) Calcula la primera forma fundamental de S.

b) Determina si S es una superficie mínima.

c) Halla la curvatura gaussiana K y la curvatura media H de S".

Lo que yo esperaría de DeepSeek-R1-Lite-Preview es que proporcionara una solución paso a paso, mostrando todos los cálculos y explicando el significado de cada resultado, así como las definiciones de los conceptos principales, como forma fundamental, superficie mínima y las distintas curvaturas.

Para que este blog sea legible, sólo podré mostrar la primera y la última parte de la respuesta, pero te animo a que pruebes tú mismo:

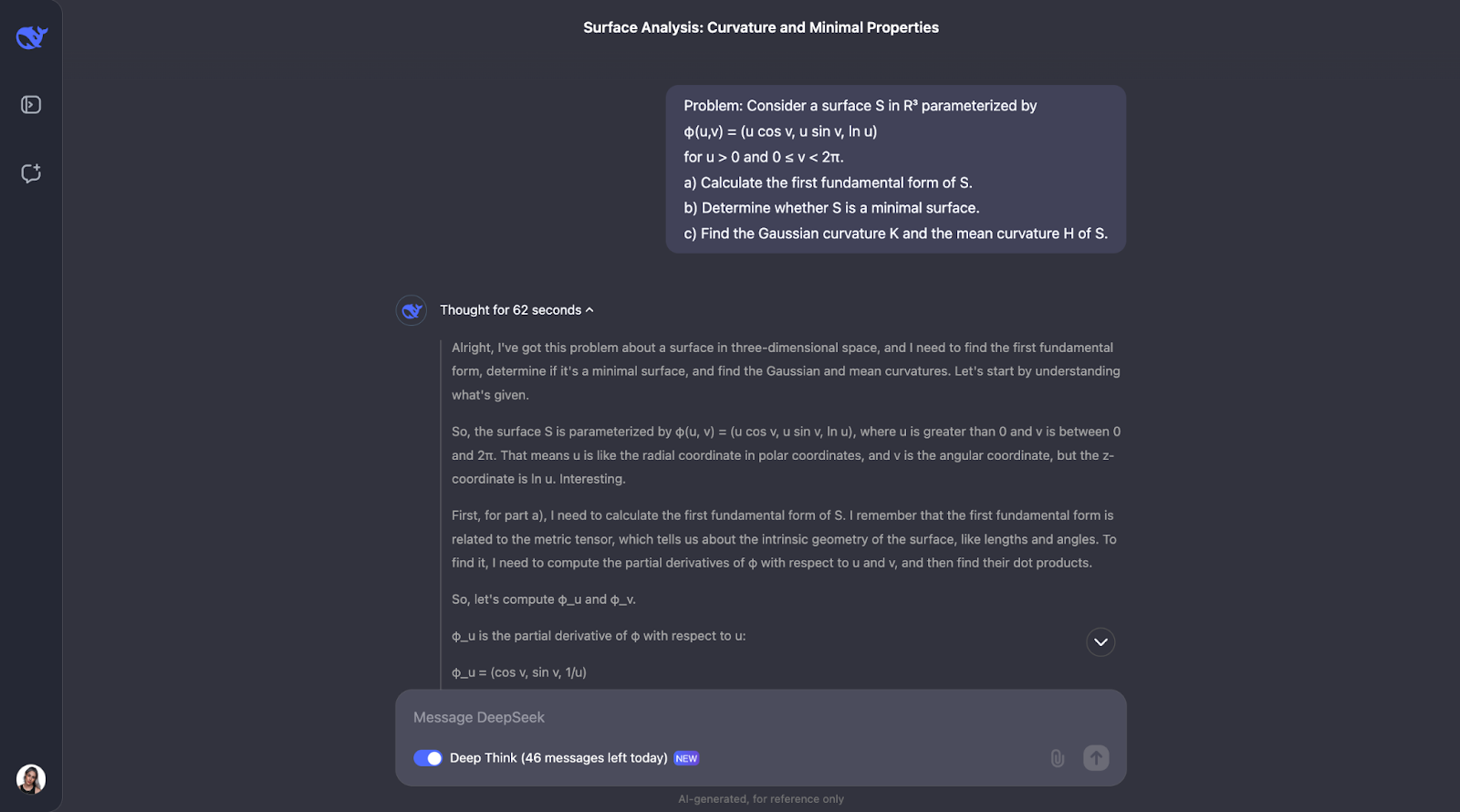
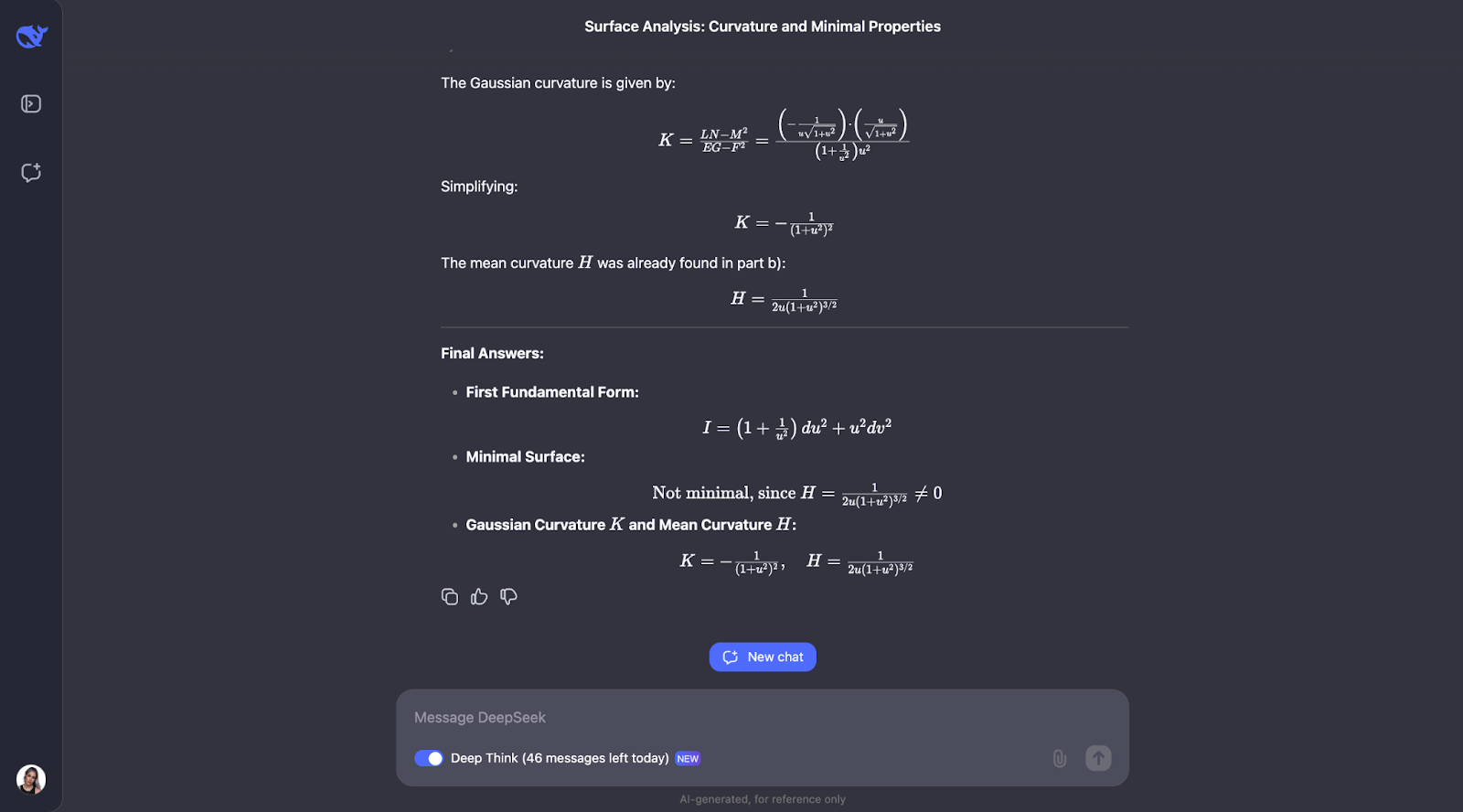
El enfoque paso a paso de sutiliza fórmulas geométricas bien conocidas y las aplica directamente, lo que hace que el razonamiento sea fácil de seguir. Sin embargo, habría esperado que comprobara su propia comprensión de los conceptos principales del problema, que no forma parte del tren de pensamiento. Para la parte B, adopta un enfoque alternativo e identifica que la superficie implicada es una superficie de revolución, lo cual es un bonito detalle.

También hay un momento en que comenta la rotación y se da cuenta de que ya tiene N, el vector normal, lo que podría entrar en conflicto con la notación del coeficiente de la segunda forma fundamental. Me hubiera gustado ver una sugerencia sobre una mejor notación, ¡ya que utilizar la misma letra para dos cosas no es una buena práctica! 

Cuando calcula la curvatura media, se da cuenta de que no es cero y se pregunta si el cálculo es correcto. Para ser minucioso, prueba otro método para volver a comprobar su trabajo.

Una vez más, el resultado es muy claro y fácil de seguir. En todos estos ejemplos, ha sido impresionante ver cómo comprueba sistemáticamente los cálculos utilizando diferentes métodos. ¡El proceso de pensamiento es siempre detallado, lógico y fácil de entender!

Prueba de codificación

Pasemos ahora a codificar las pruebas.

Python

La primera que voy a probar es:

"Implementa una función en Python que encuentre la subcadena palindrómica más larga de una cadena dada. La función debe tener una complejidad temporal mejor que O(n^3)."

Intento evaluar la capacidad del modelo para diseñar algoritmos eficientes e implementarlos en código. Esperaría una solución utilizando programación dinámica o el algoritmo de Manacher, con una explicación clara del enfoque y la complejidad temporal análisis.

La salida es muy-muy larga, y sólo muestro la primera y la última parte:

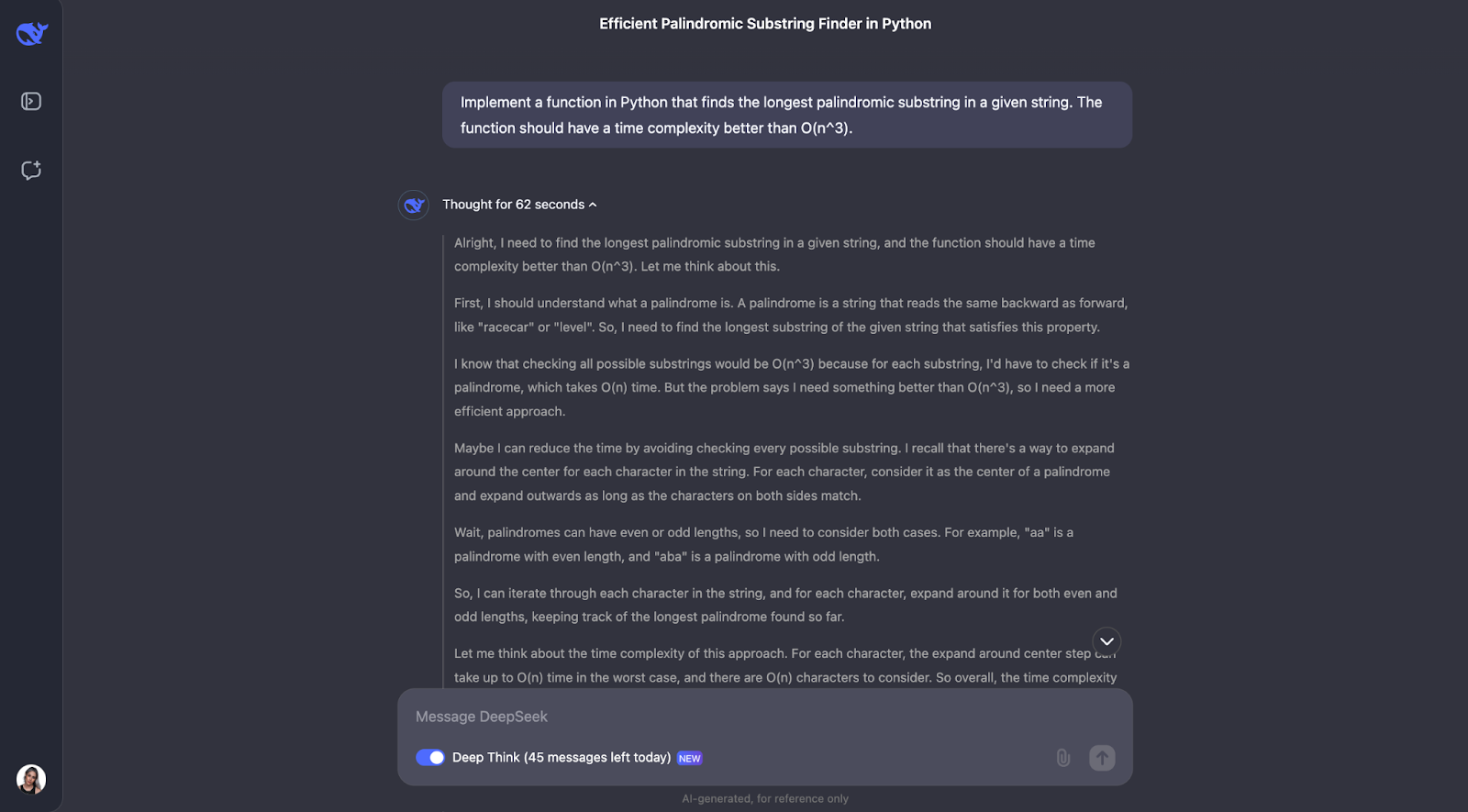
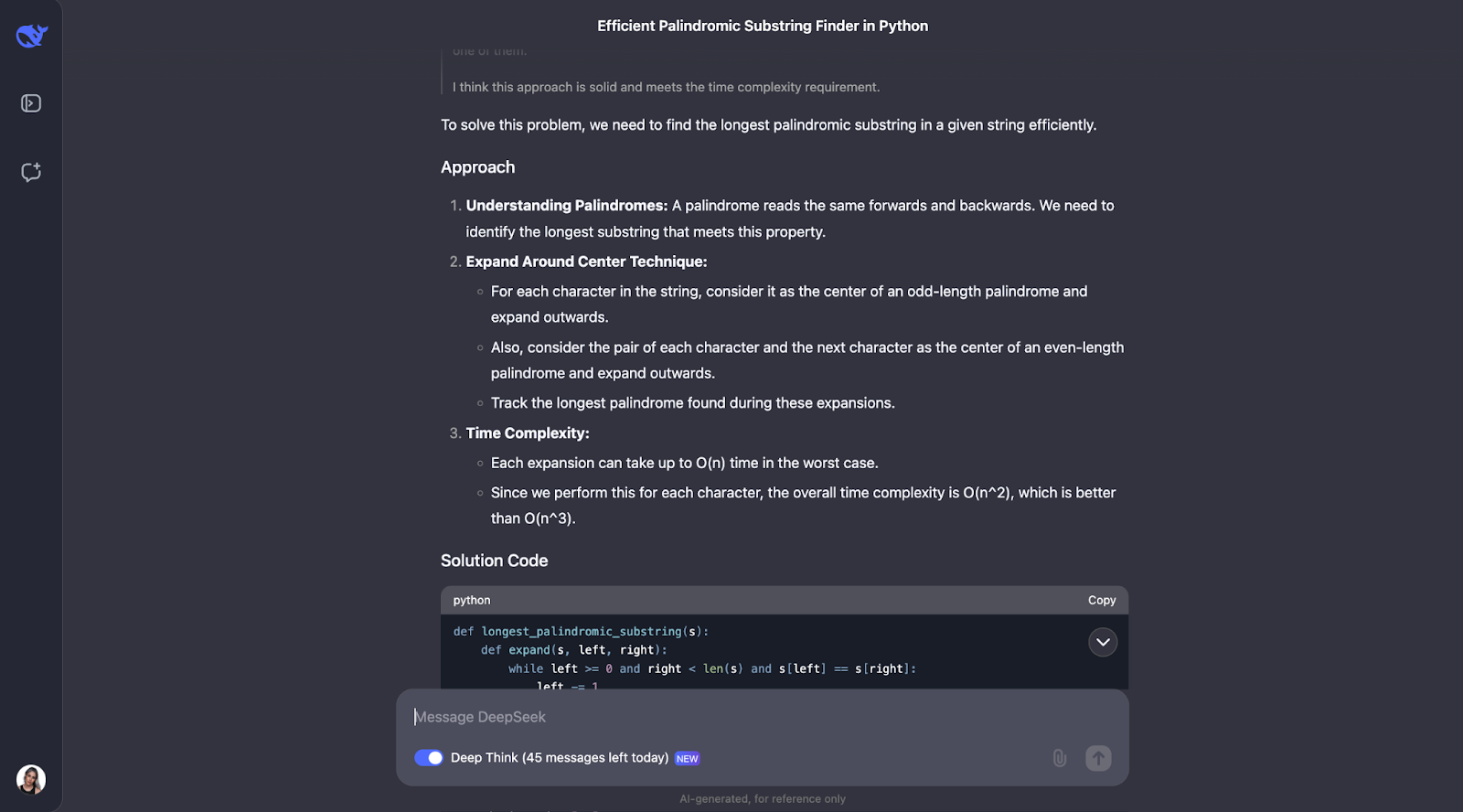
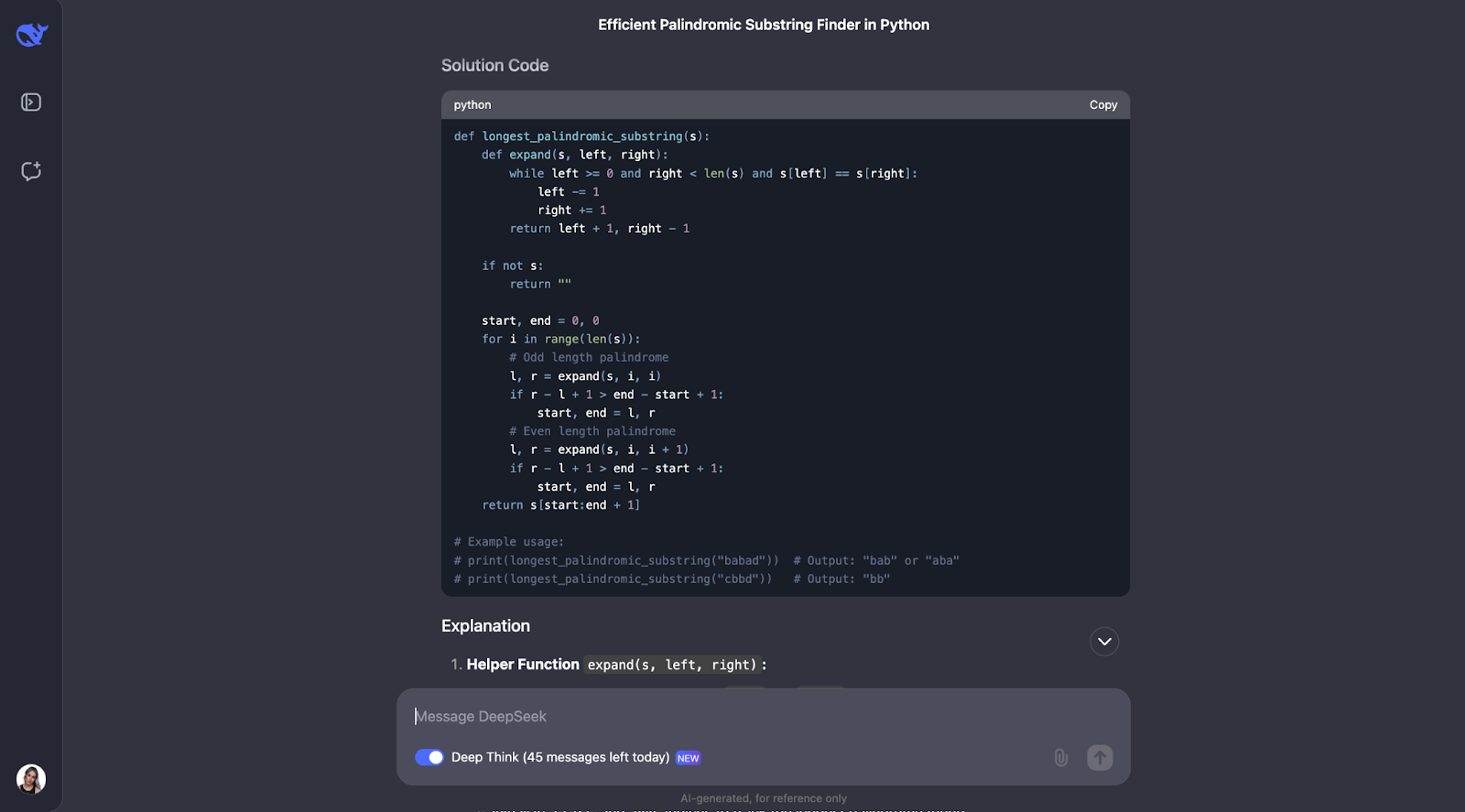
Creo que el modelo ha resuelto muy bien el problema de encontrar la subsecuencia palindrómica más larga. Su enfoque fue inteligente, eficaz y claramente explicado.

En lugar de forzar cada posible subcadena, lo que sería lento, utilizó una ingeniosa técnica de "expansión alrededor de los centros". Este método manejaba tanto los palíndromos de longitud impar como "aba", como los de longitud par como "abba". Llevaba la cuenta del palíndromo más largo que encontraba a su paso. El resultado fue un algoritmo que se ejecuta en tiempo O(n^2), mucho más rápido que una solución O(n^3). 

Lo que más me impresiona de esta respuesta es la claridad con que se ha presentado. DeepSeek desglosó el problema en pasos comprensibles, explicó detalladamente su proceso de pensamiento e incluso incluyó ejemplos prácticos. Por ejemplo, mostraba cómo el algoritmo se expande alrededor del centro de "racecar" o "abba" para encontrar el palíndromo correcto. En mi opinión, la función de ayuda para expandirse alrededor de un centro era especialmente buena: hacía que el código fuera modular y fácil de seguir.

Dicho esto, habría esperado que considerara el algoritmo de Manacher, que es una solución O(n) más rápida. Definitivamente es más complejo de implementar, pero es útil para casos en los que el rendimiento es crítico, y habría esperado que el modelo lo hubiera señalado. 

También me di cuenta de que el resultado no explicaba explícitamente cómo trata el algoritmo los casos especiales, como una cadena vacía o una cadena con todos los caracteres idénticos (por ejemplo, "aaaa"). Estos casos funcionarían, pero yo habría esperado que al menos lo discutiera. 

Por último, me parece bien que comente el resultado esperado para los usos de ejemplo. Sin embargo, cuando ejecuté el código, sólo se imprimió la primera opción del uso del primer ejemplo. Habría sido estupendo que el código considerara todas las soluciones posibles y que todas ellas se imprimieran.

JavaScript

Intentemos un problema de codificación diferente en otro lenguaje de programación.

"Escribe una función en JavaScript que determine si un número dado es primo"

Para facilitar la lectura, sólo muestro la primera y la última parte (aunque la cadena de pensamiento era un poco más corta esta vez):

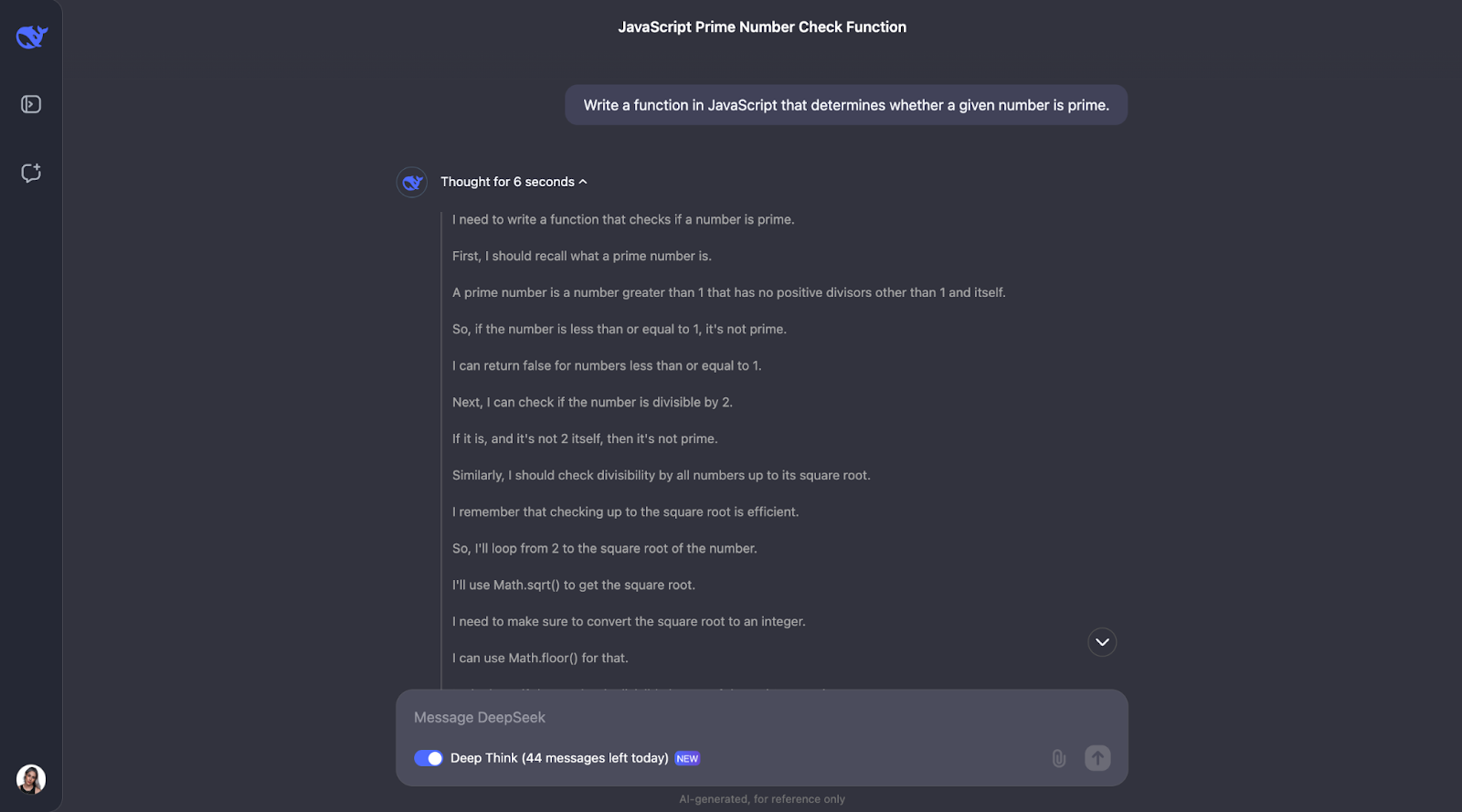
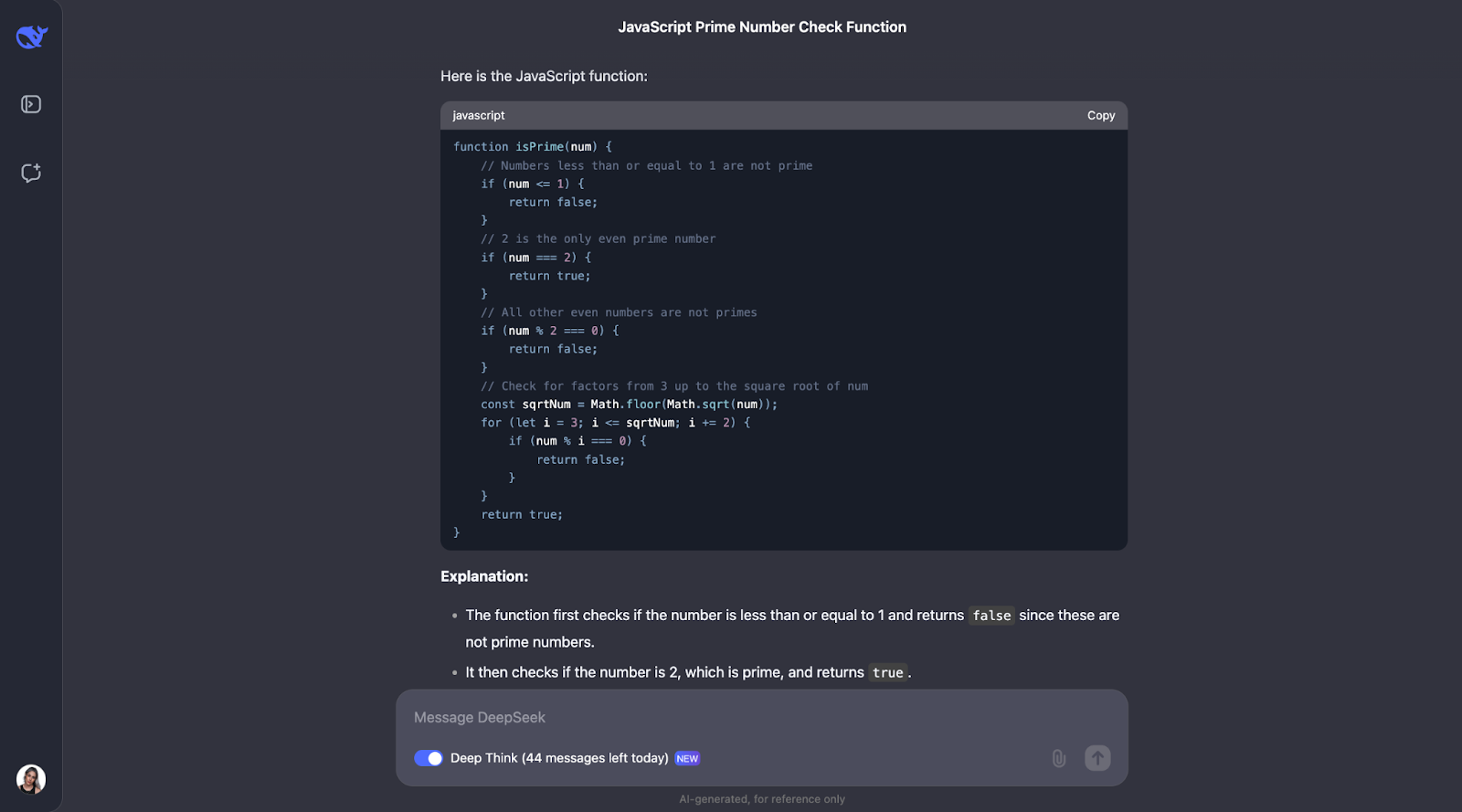
Creo que podemos ver aquí un patrón para el proceso de pensamiento. La mayoría de las veces, empieza por definir los conceptos clave que aparecen en el problema. Así, por ejemplo, para este problema, define qué es un número primo.

Después, el proceso de pensamiento tiene sentido y llega a pasos optimizados. En primer lugar, cubre lo básico: los números menores o iguales que 1 no son primos, y 2 es el único número primo par. A partir de ahí, comprueba si el número es divisible por cualquier número impar hasta la raíz cuadrada del número. Esto ahorra tiempo porque evita cálculos innecesarios. Además, en lugar de comprobar cada número, omite todos los números pares más allá del 2, lo que hace que el proceso sea aún más rápido. La función utiliza Math.sqrt para encontrar la raíz cuadrada, lo que limita hasta dónde tiene que comprobar, manteniéndola eficiente y sencilla. 

De nuevo, prueba también con pequeños ejemplos, como en el problema anterior, como números primos y no primos conocidos, para asegurarte de que funciona como se espera.

Sin embargo, hay margen de mejora. Por ejemplo, la función no comprueba si la entrada es realmente un número, por lo que podría gestionar mejor los errores. También podría incluir atajos para números como los acabados en 0 o 5, que obviamente no son primos (excepto el propio 5). Añadir un poco más de explicación sobre por qué se salta los números pares o sólo comprueba hasta la raíz cuadrada también ayudaría a los principiantes a entenderlo mejor, creo yo.

Por último, habría esperado que el código tuviera algunas pruebas de uso de ejemplo, del mismo modo que antes nos dio las del código Python en la prueba.

Razonamiento lógico

Pasemos ahora a las pruebas de razonamiento lógico.

El problema del lobo, la cabra y la col

Voy a probar un puzzle clásico:

"Un hombre tiene que cruzar un río con un lobo, una cabra y un repollo. Su barco sólo puede transportarse a sí mismo y a otra cosa. Si se le dejara solo, el lobo se comería a la cabra, y la cabra se comería la col. ¿Cómo puede cruzarlo todo de forma segura?"

Esperaría que el modelo proporcionara la siguiente respuesta:

1. Comienza: Hombre, Lobo, Cabra, Col por un lado
2. El hombre lleva a la cabra al otro lado (el lobo y la col están a salvo juntos)
3. El hombre vuelve solo
4. Un hombre lleva a un lobo al otro lado
5. El hombre trae de vuelta a la cabra (el lobo y la cabra no pueden estar solos)
6. Un hombre se lleva un repollo al otro lado
7. El hombre vuelve solo
8. Un hombre lleva a una cabra al otro lado
9. Fin: Todos a salvo a través de

Pero veamos cómo maneja el proceso de pensamiento, ¡ya que no estoy seguro de qué esperar!

También necesito truncar esta salida para que sea legible:

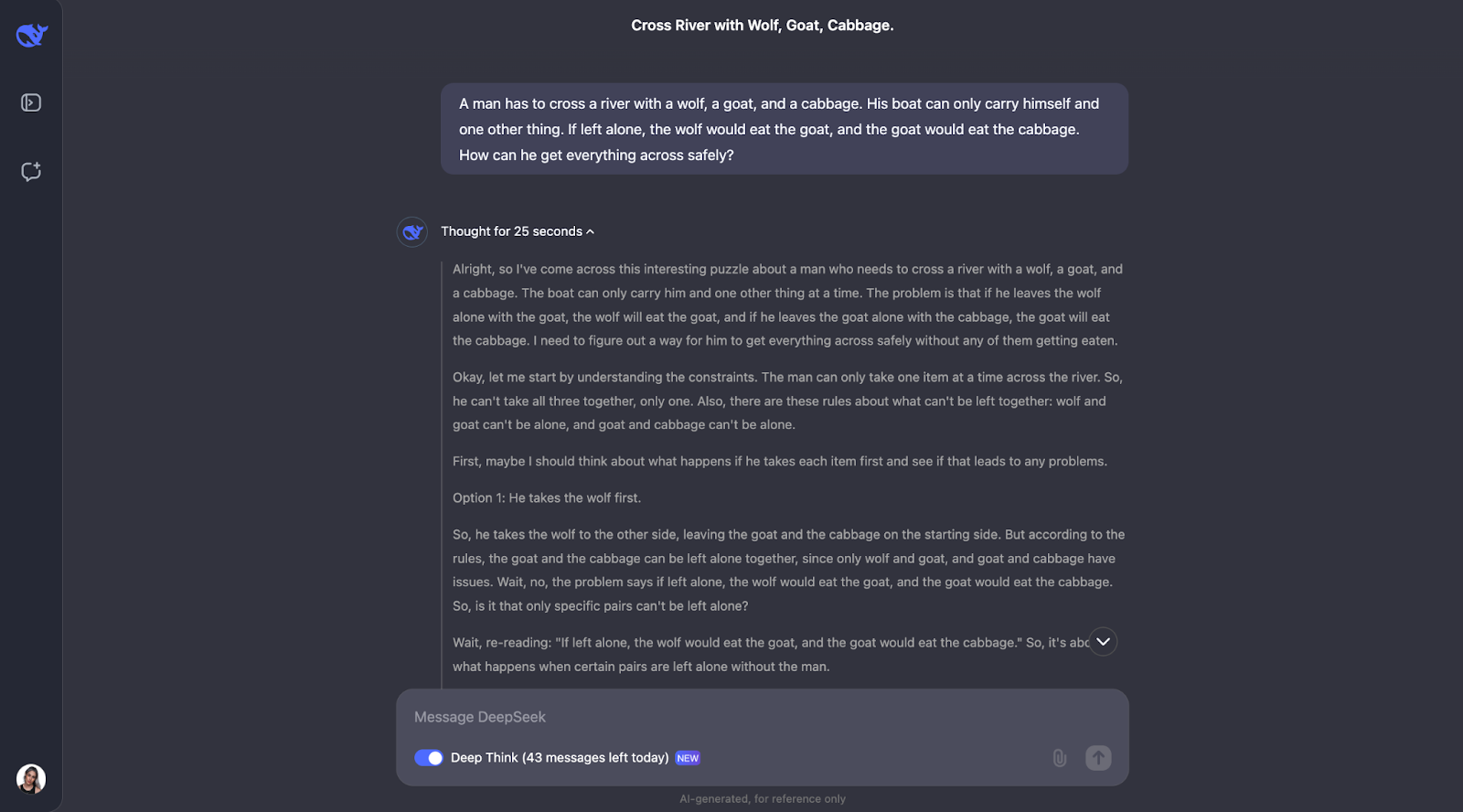
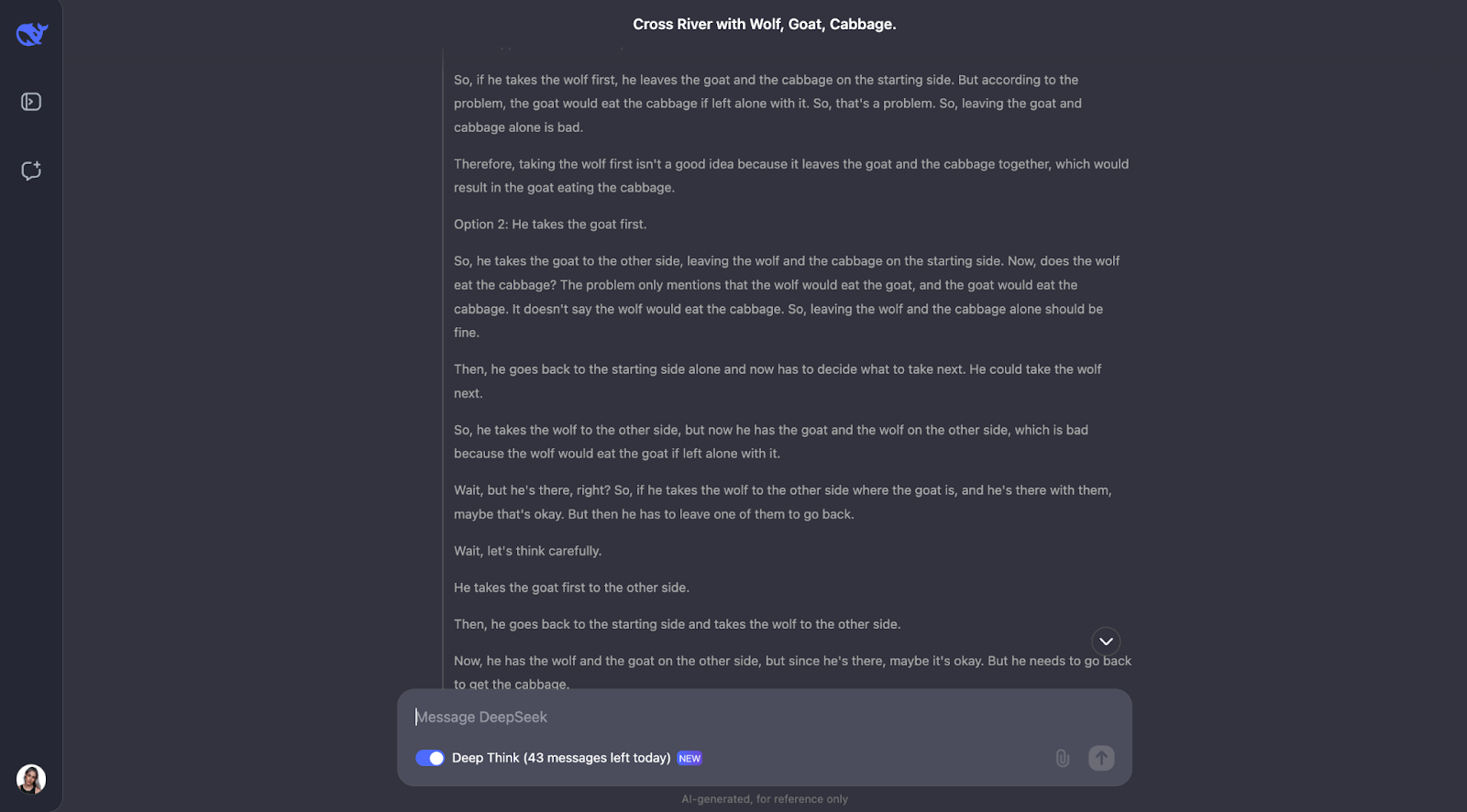
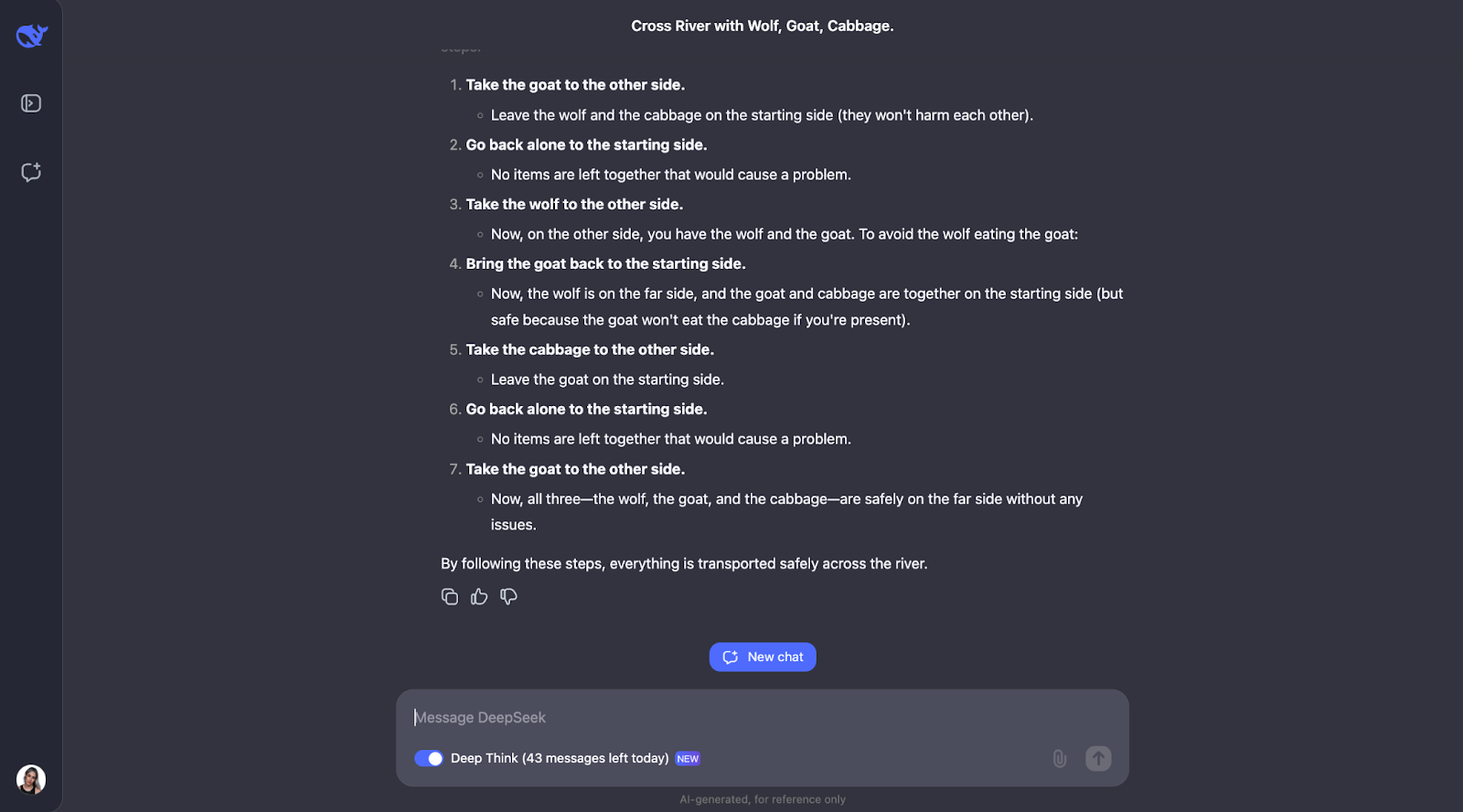
El modelo resuelve muy bien este clásico rompecabezas de cruce de ríos. Piensa detenidamente en las normas y comprueba distintas posibilidades. Comprende que algunas parejas, como el lobo y la cabra o la cabra y el repollo, no se pueden dejar solas. También revisa las limitaciones al principio. A partir de ahí, examina qué ocurriría si el hombre llevara primero cada objeto al otro lado del río y averigua si eso crea algún problema.

Lo que me parece realmente bonito es cómo el modelo ajusta su plan cuando algo no funciona. Por ejemplo, cuando intenta coger primero al lobo, pero se da cuenta de que eso causa problemas, y entonces se replantea los pasos. Este método de ensayo y error se parece mucho a cómo nosotros mismos, como humanos, podríamos resolver el puzzle.

Al final, el modelo da con la solución correcta y la explica de forma clara y paso a paso.

Puzzle de las bolas de pesaje

Probemos con otra:

"Tienes 12 bolas, todas idénticas en apariencia. Una bola es más pesada o más ligera que el resto. Utilizando una balanza, encuentra la bola impar y determina si es más pesada o más ligera en sólo tres pesadas".

Este rompecabezas lógico clásico pone a prueba la capacidad del modelo para dar con una estrategia óptima utilizando el razonamiento deductivo. A ver qué pasa. La salida era muy-muy larga esta vez, así que tendré que saltar directamente a la respuesta de :

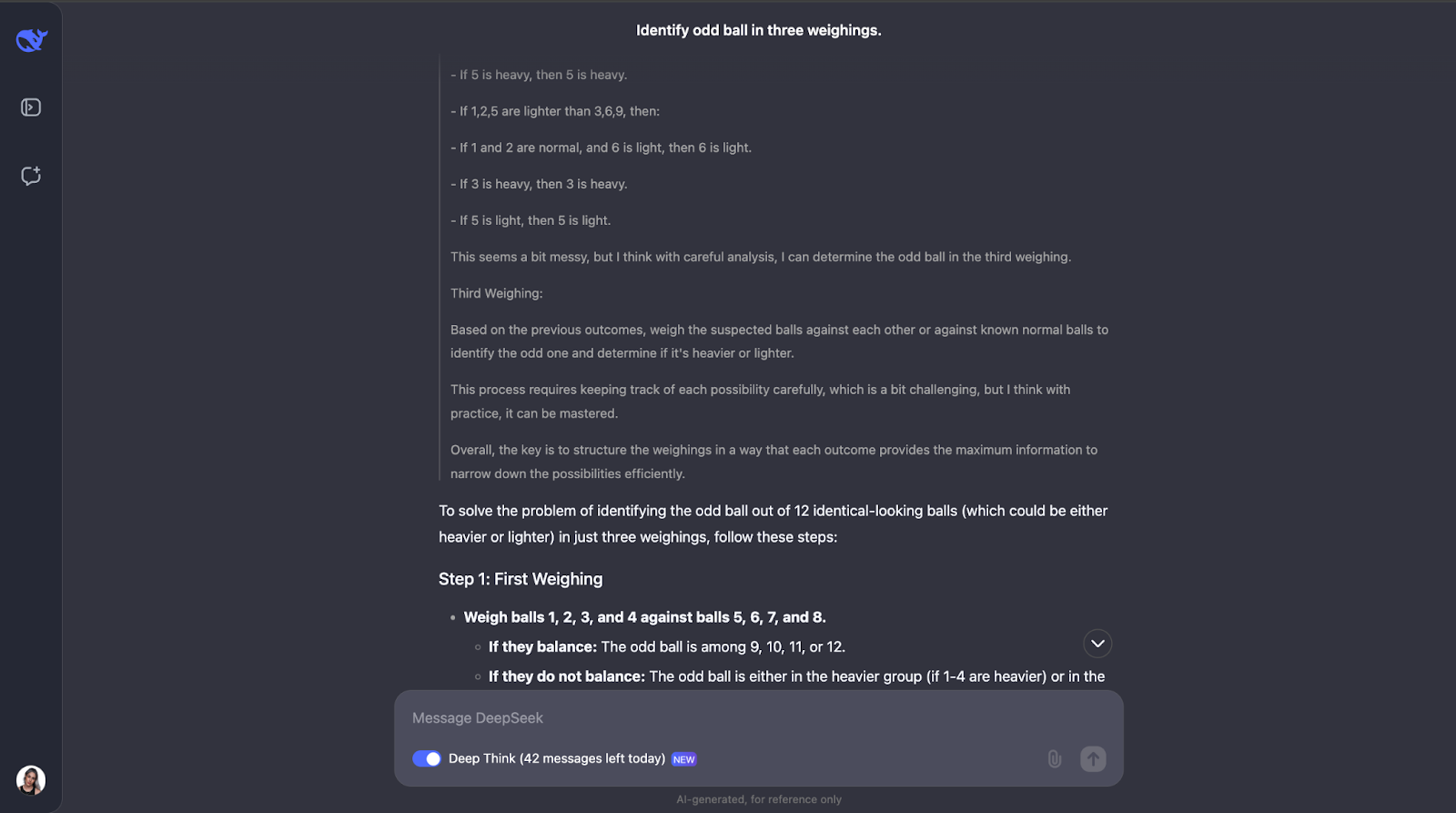
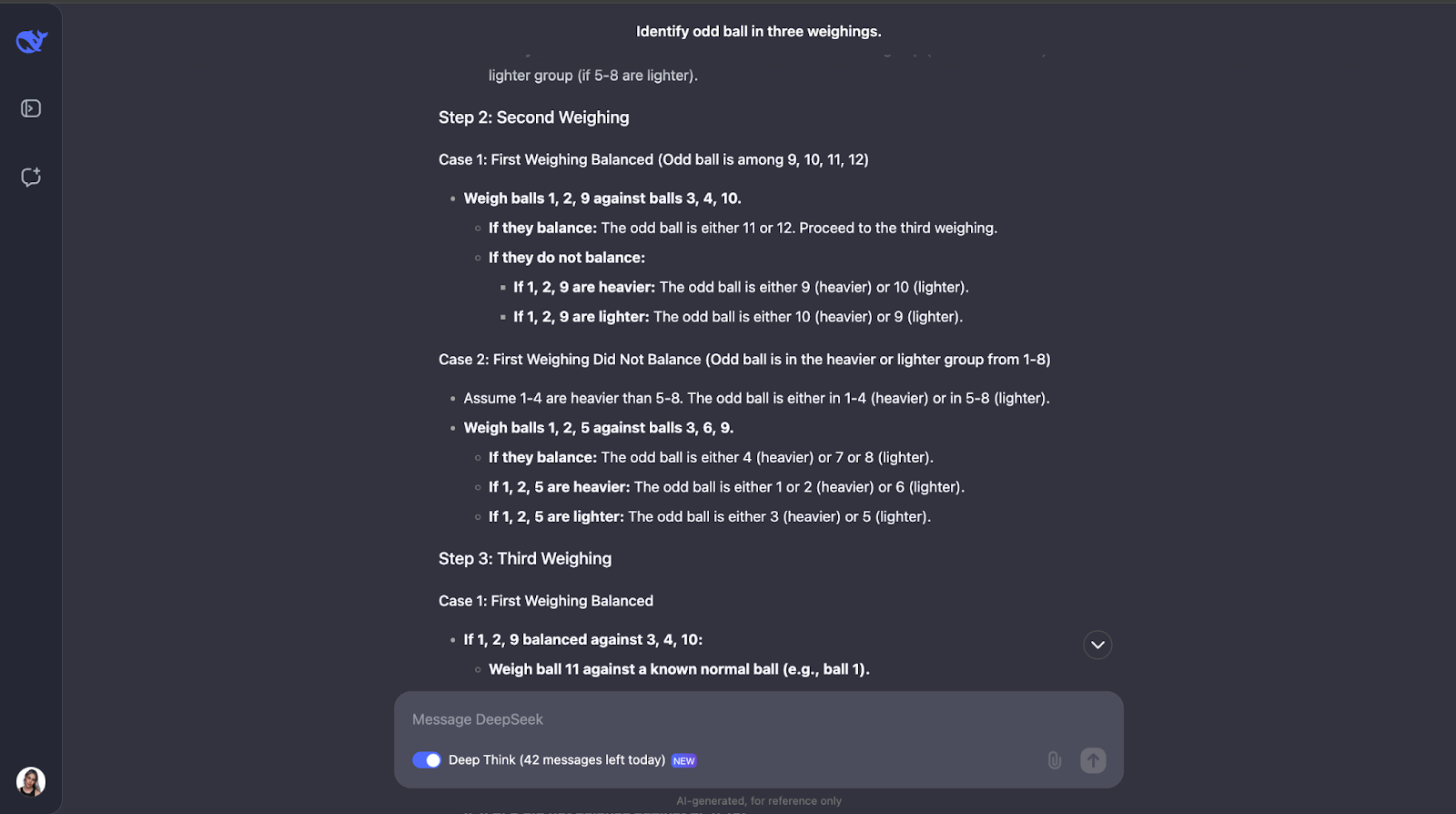
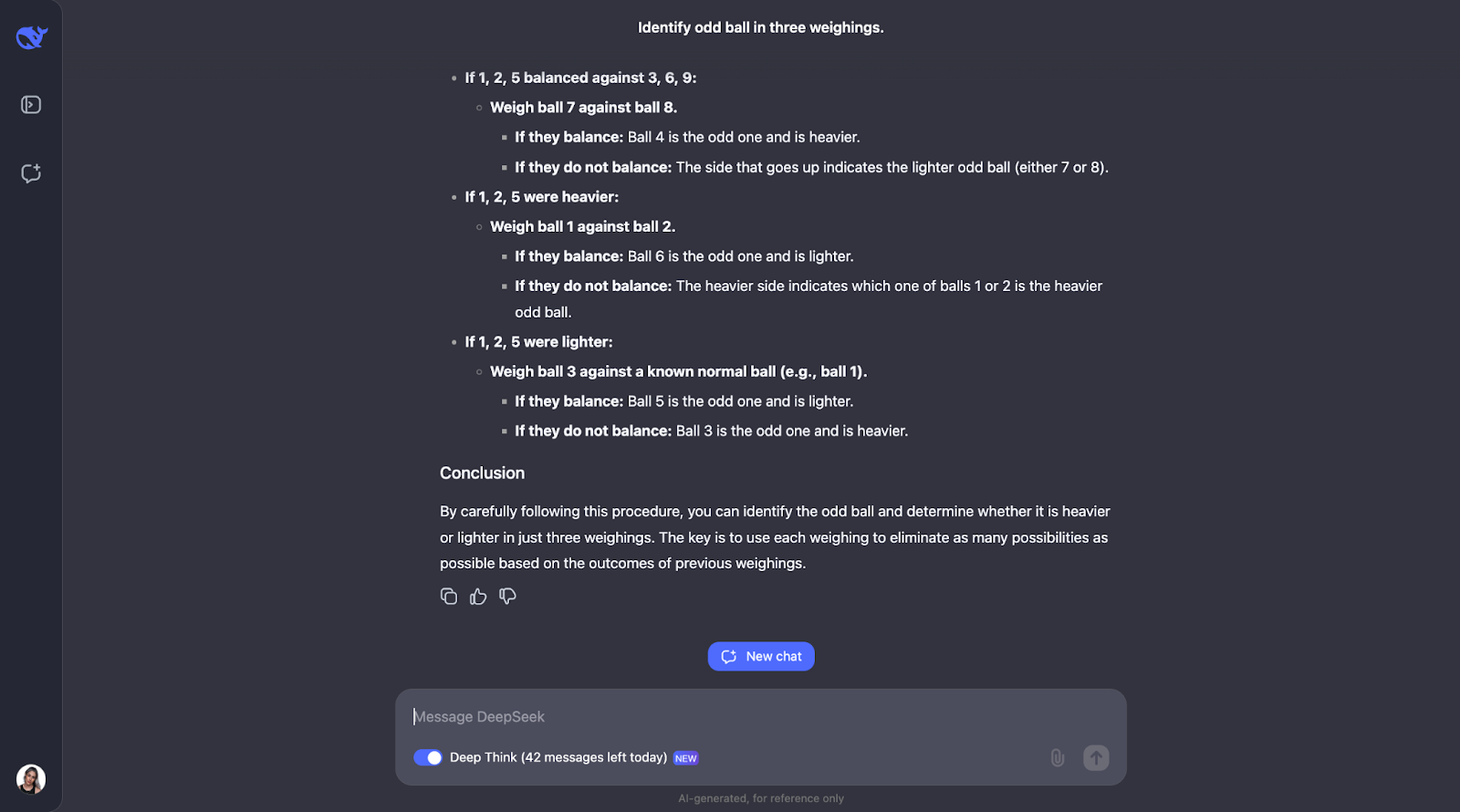
¡Otro en el que he subestimado totalmente la longitud de la salida! El modelo se da cuenta de que resolver este puzzle requiere una planificación cuidadosa porque sólo tienes tres intentos. También calcula el número de resultados y posibilidades.

El planteamiento del modelo es inteligente porque cada pesaje elimina tantas posibilidades como sea posible. Planifica todos los resultados -tanto si la balanza se equilibra como si se inclina- y ajusta el siguiente paso en función de lo que ocurra. Es muy detallado, pero los pasos son claros y lógicos, lo que hace que sea muy fácil de seguir, aunque sea largo,

Una cosa que me ha gustado mucho es que, cuando el planteamiento empieza a ser demasiado complejo, aplica un enfoque más sistemático o sencillo. Sin embargo, creo que para problemas como éste, en los que es necesario hacer un seguimiento de los distintos casos, resultados y posibilidades, añadir un diagrama o gráfico podría ayudar a la gente a visualizar el hilo de pensamiento y comprender mejor el resultado.

DeepSeek-R1-Lite-Preview Benchmarks

En esta sección, compararé DeepSeek con otros modelos como o1-preview y GPT-4o en términos de rendimiento en diferentes pruebas de referencia. Cada uno se centra en una habilidad diferente, para que podamos ver qué modelos son mejores en qué. Veamos los puntos de referencia medidos por DeepSeek:

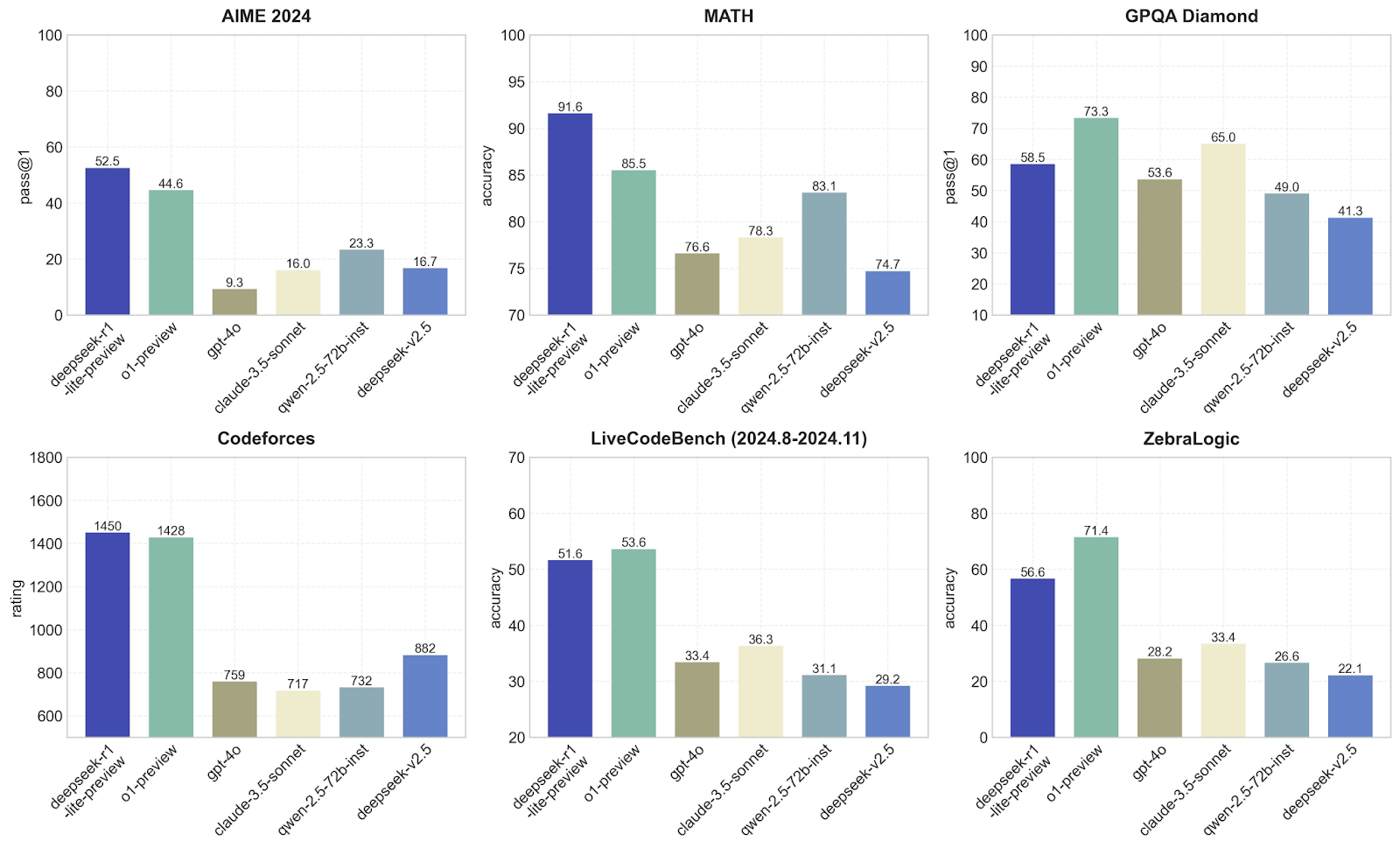
AIME 2024

DeepSeek-r1-lite-preview es claramente el mejor aquí, con un pass@1 de 52,5, seguido de o1-preview con 44,6. Otros modelos, como GPT-4o y claude-3.5-sonnet, obtienen resultados mucho peores, con puntuaciones inferiores a 23. Esto sugiere que el modelo DeepSeek-r1-lite-preview es bastante bueno manejando el tipo de problemas matemáticos o lógicos avanzados específicos de los puntos de referencia AIME, lo cual no me sorprende después de las pruebas que he realizado.

MATEMÁTICAS

DeepSeek-v1 domina de nuevo con una impresionante precisión de 91,6, muy por delante de o1-preview (85,5) y mucho mejor que otros modelos como GPT-4o, que luchan por alcanzar 76,6. Esto demuestra que DeepSeek es excelente resolviendo problemas matemáticos, lo que confirma mi hipótesis a partir de las pruebas empíricas que realicé anteriormente: ¡hasta ahora no hay sorpresas!

GPQA Diamante

Aquí, o1-preview obtiene mejores resultados que DeepSeek-v1, con un pass@1 de 73,3 frente a 58,5. Otros modelos, como el GPT-4o, se quedan atrás con un 53,6. Esto sugiere que o1-previsión es más adecuado para tareas que implican responder preguntas o resolver problemas basados en el razonamiento lógico. DeepSeek sigue teniendo un rendimiento sólido, pero no es tan bueno como o1-preview.

Código de fuerzas

En cuanto a la programación competitiva, DeepSeek-v1 (1450) y 01-preview (1428) están casi empatados en el primer puesto, mientras que otros modelos como GPT-4o sólo alcanzan una puntuación en torno a 759. Como era de esperar, esto demuestra que estos dos modelos son excelentes a la hora de comprender y generar código para los retos de programación.

LiveCodeBench

Esto pone a prueba las habilidades de codificación a lo largo del tiempo, y o1-preview supera ligeramente a DeepSeek-v1 (53,6 frente a 53,5). 51.6). Otros modelos, como el GPT-4o, se quedan muy atrás, con un 33,4. De nuevo, esto demuestra que tanto DeepSeek como 01-preview son adecuados para la codificación, pero que 01-preview es un poco mejor en estas tareas.

ZebraLogic

o1-preview toma la delantera aquí con una precisión del 71,4, frente al 56,6 de DeepSeek-v1. Otros modelos lo hacen mucho peor. Esto demuestra que o1-preview es mejor en el manejo de tareas lógicas abstractas como ZebraLogic, que requieren un pensamiento más creativo o out-of-the-box, lo que coincide con los resultados que obtuve en las pruebas, ya que la creatividad definitivamente no era el fuerte de DeepSeek-v1.

Estos gráficos corroboran que DeepSeek-v1 es asombroso en los retos matemáticos y de programación. Yo diría que o1-preview es más equilibrado y funciona bien en una gama más amplia de tareas, lo que lo hace más versátil.

Veamos ahora este gráfico:

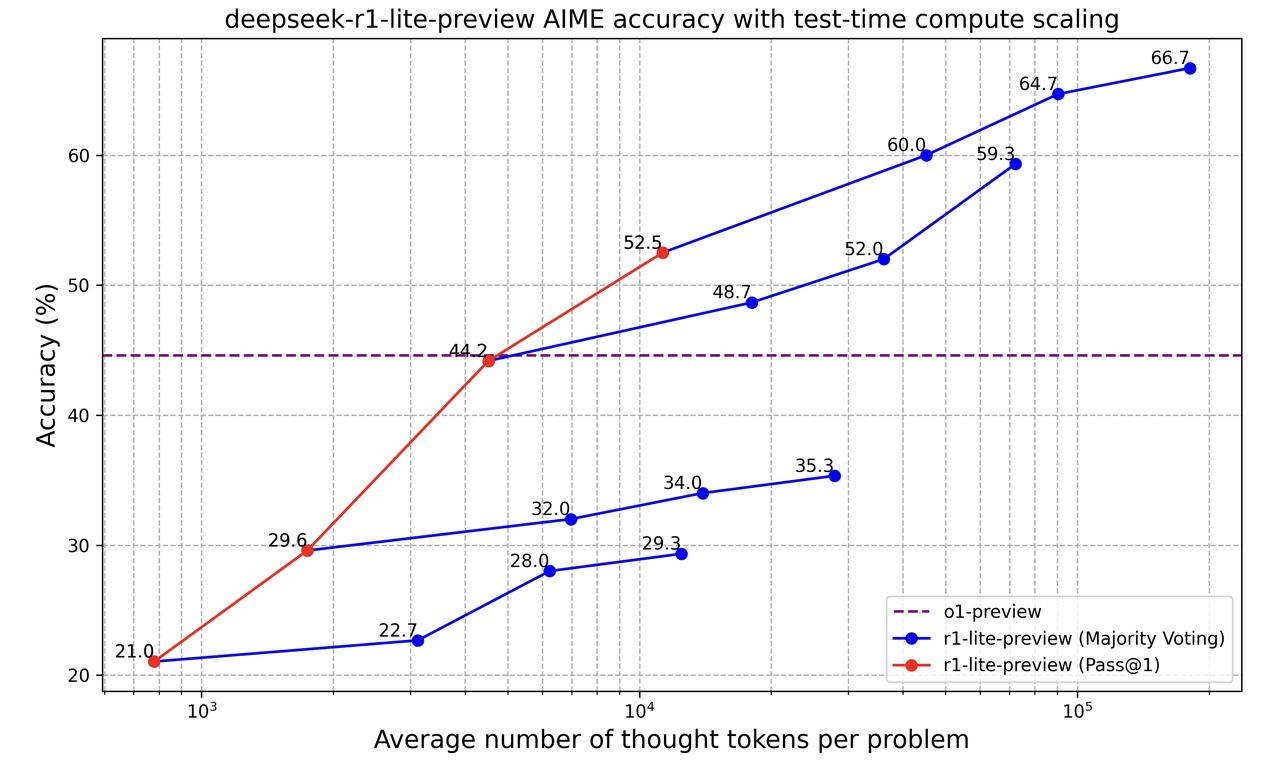
Este gráfico muestra cómo el modelo "deepseek-r1-lite-preview" mejora en la resolución de problemas a medida que procesa más información (medida por el número de "fichas de pensamiento" que utiliza). Compara dos formas de medir la precisión del modelo:

1. Pase@1 (línea roja): Así de preciso es el modelo cuando da su primera respuesta. A medida que utiliza más tokens, su precisión mejora del 21% al 52,5%. Esto significa que el modelo hace mejor su trabajo cuando tiene más tiempo para pensar, incluso sólo para su primera respuesta.
2. Votación por mayoría (línea azul): Aquí, el modelo da múltiples respuestas y elige la que sugiere con más frecuencia (voto mayoritario). Este método comienza con un 22,7% y mejora hasta un 66,7% a medida que se utilizan más fichas. Siempre es más preciso que el enfoque de la primera respuesta, lo que demuestra que dar al modelo múltiples intentos le ayuda a tomar mejores decisiones.

La línea discontinua morada representa el modelo o1-previsión que tiene una precisión constante. Al principio, o1-preview es mejor, pero a medida que se permite a DeepSeek r1-lite-preview utilizar más tokens de pensamiento, supera a o1-preview y se vuelve mucho más preciso.

Así que, básicamente, este gráfico muestra que dejar que DeepSeek r1-lite-preview piense más y lo intente varias veces mejora su precisión.

Conclusión

¿Es DeepSeek-r1-lite-preview mejor que o1-preview de OpenAI? Depende de la tarea. Yo diría que sí para los problemas de matemáticas y codificación. Para el razonamiento lógico, depende de la tarea. 

Lo que realmente me sorprendió fue cómo razonaba algunas de las pruebas. Realmente me hizo reflexionar sobre lo que significa realmente que un modelo "piense" y cómo se le ocurren los planteamientos de razonamiento.

Si sientes curiosidad por este modelo, ¿por qué no lo pruebas tú mismo? Pruébalo en las tareas que te interesen y comprueba su rendimiento: ¡puede que te sorprenda tanto como a mí!