Búsqueda en profundidad en Python: Guía con ejemplos

Imagina que intentas trazar la ruta más rápida a través de un laberinto, identificar conexiones entre personas en una red social o encontrar la forma más eficiente de transmitir datos a través de Internet. Estos retos comparten un objetivo común: explorar sistemáticamente las relaciones entre distintos puntos. La búsqueda amplia es un algoritmo que puede ayudarte a conseguirlo.

La búsqueda exhaustiva se aplica a una amplia gama de problemas de la ciencia de datos, desde el recorrido de grafos a la búsqueda de rutas. Es especialmente útil para encontrar el camino más corto en grafos no ponderados. Sigue leyendo y trataré en detalle la búsqueda amplia y mostraré una implementación en Python. Si, al empezar, quieres más ayuda en Python , inscríbete en nuestro curso muy completo de Introducción a Python .

¿Qué es la búsqueda amplia?

La búsqueda en profundidad (BFS) es un algoritmo de recorrido de grafos que explora un grafo o árbol nivel a nivel. Partiendo de un nodo origen especificado, el BFS visita a todos sus vecinos inmediatos antes de pasar al siguiente nivel de nodos. Esto garantiza que los nodos de la misma profundidad se procesen antes de profundizar más. Por ello, el BFS es útil para problemas que requieren examinar todos los caminos posibles de forma estructurada y sistemática.

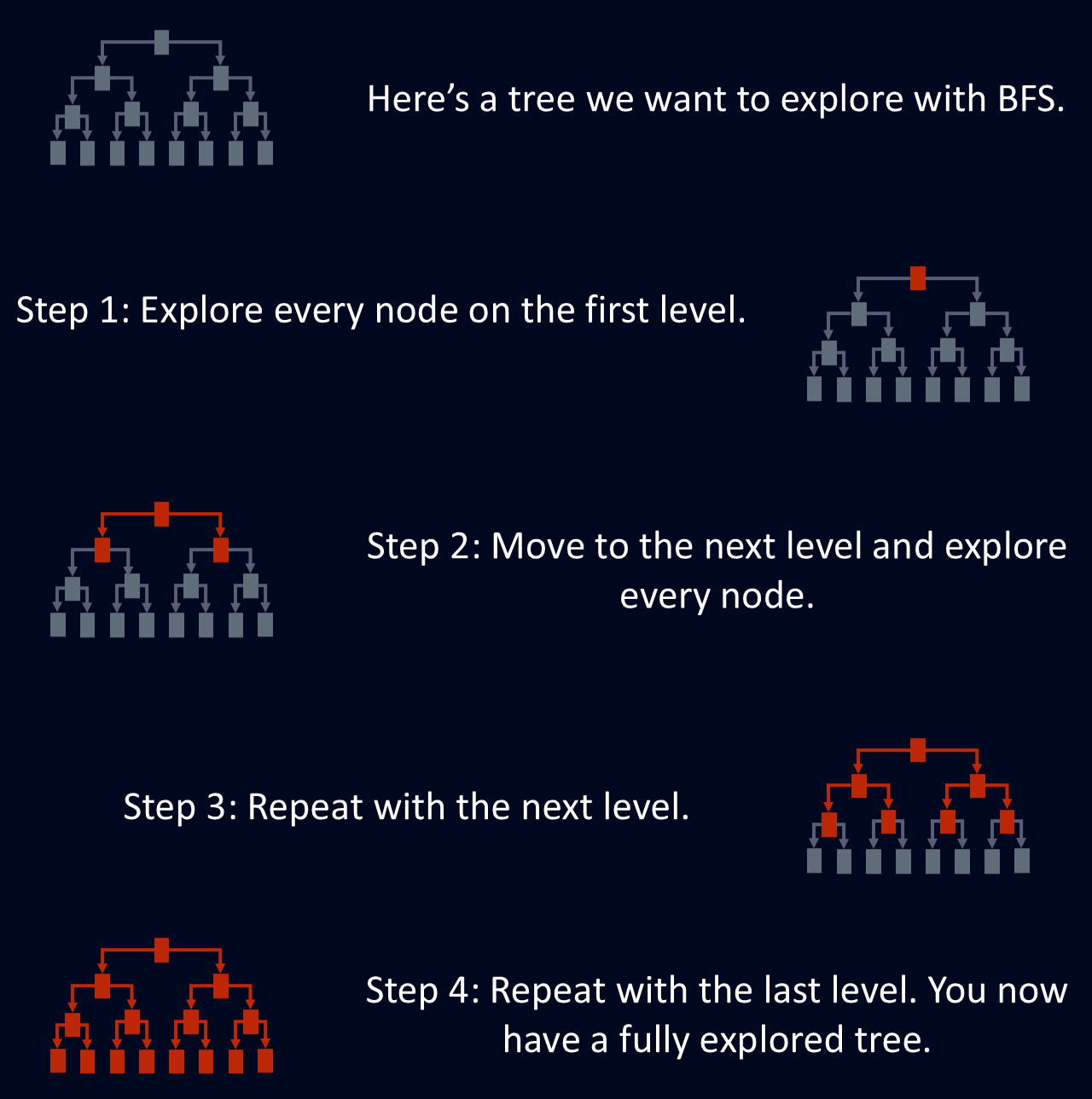
BFS es útil para encontrar la ruta más corta entre nodos, porque la primera vez que BFS llega a un nodo, utiliza la ruta más corta. Esto hace que el BFS sea útil para problemas como el encaminamiento de redes, donde el objetivo es encontrar la ruta más eficiente entre dos puntos. El diagrama siguiente muestra una explicación simplificada de cómo la BFS explora un árbol.

Características principales del algoritmo de búsqueda Breadth-First

La búsqueda "primero el ancho" está diseñada para explorar un grafo o árbol visitando todos los vecinos de un nodo antes de pasar a la siguiente capa. Este recorrido estructurado garantiza que se exploren todos los nodos de una determinada profundidad antes de adentrarse en la estructura. Este enfoque por niveles hace que el BFS sea una forma sistemática y fiable de navegar por redes complejas.

Método transversal

BFS explora cada nodo en el nivel de profundidad actual antes de pasar al siguiente. Esto significa que todos los nodos situados a una distancia determinada del punto de partida se procesan antes de avanzar más.

Implementación basada en colas

BFS utiliza una cola para gestionar los nodos que necesitan ser visitados. El algoritmo procesa un nodo, añade sus vecinos no visitados a la cola y continúa este patrón. La cola funciona según el orden de entrada, garantizando que los nodos se exploran en el orden en que se descubren.

Camino más corto garantizado en grafos no ponderados

En grafos no ponderados, o grafos en los que cada enlace tiene la misma longitud, BFS garantiza encontrar el camino más corto entre nodos. Como el BFS explora a los vecinos nivel por nivel, la primera vez que llega a un nodo, lo hace por la ruta más corta posible. Esto hace que el BFS sea especialmente eficaz para resolver los problemas del camino más corto, en situaciones en las que todas las aristas tienen el mismo peso.

Aplicable tanto a grafos como a árboles

BFS funciona tanto con grafos como con árboles. Un grafo es una red de nodos conectados que puede tener ciclos, como una red social, mientras que un árbol es una jerarquía con una raíz y sin ciclos, como un pedigrí. La BFS es útil para ambas cosas, lo que la hace ampliamente aplicable a una gran variedad de tareas.

Implementación de la búsqueda exhaustiva en Python

Vamos a demostrar en Python el algoritmo de búsqueda en primer lugar en un árbol. Si necesitas refrescar tus conocimientos de Python, echa un vistazo al curso de Programación en Python en DataCamp. Para más información sobre diferentes estructuras de datos y los algoritmos, sigue nuestro curso Estructuras de Datos y Algoritmos en Python y lee nuestro Estructuras de Datos: Una guía completa con ejemplos de Python tutorial.

Empecemos. En primer lugar, tenemos que configurar un árbol de decisión sencillo para que busque nuestro BFS.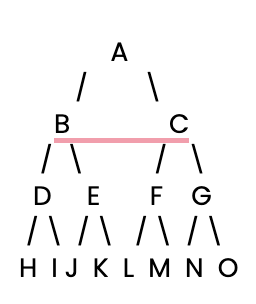

A continuación, definiremos este sencillo árbol de decisión utilizando un diccionario Python, donde cada clave es un nodo, y su valor es una lista de los hijos del nodo.

# Define the decision tree as a dictionary
tree = {
    'A': ['B', 'C'],  # Node A connects to B and C
    'B': ['D', 'E'],  # Node B connects to D and E
    'C': ['F', 'G'],  # Node C connects to F and G
    'D': ['H', 'I'],  # Node D connects to H and I
    'E': ['J', 'K'],  # Node E connects to J and K
    'F': ['L', 'M'],  # Node F connects to L and M
    'G': ['N', 'O'],  # Node G connects to N and O
    'H': [], 'I': [], 'J': [], 'K': [],  # Leaf nodes have no children
    'L': [], 'M': [], 'N': [], 'O': []   # Leaf nodes have no children
}

Ahora vamos a implementar el algoritmo BFS en Python. BFS funciona visitando todos los nodos del nivel actual antes de pasar al siguiente nivel. Utilizaremos una cola para gestionar qué nodos visitar a continuación.

from collections import deque  # Import deque for efficient queue operations

# Define the BFS function
def bfs(tree, start):
    visited = []  # List to keep track of visited nodes
    queue = deque([start])  # Initialize the queue with the starting node

    while queue:  # While there are still nodes to process
        node = queue.popleft()  # Dequeue a node from the front of the queue

        if node not in visited:  # Check if the node has been visited
            visited.append(node)  # Mark the node as visited
            print(node, end=" ")  # Output the visited node

            # Enqueue all unvisited neighbors (children) of the current node
            for neighbor in tree[node]:
                if neighbor not in visited:
                    queue.append(neighbor)  # Add unvisited neighbors to the queue

Ahora que hemos creado nuestra función BFS, podemos ejecutarla en el árbol, empezando por el nodo raíz A.

# Execute BFS starting from node 'A'
bfs(tree, 'A')

Al ejecutarlo, muestra cada nodo en el orden en que fue visitado.

A B C D E F G H I J K L M N O

BFS en Árboles vs. Gráficos

El patrón de recorrido de BFS es sencillo en los árboles, ya que son intrínsecamente acíclicos. El algoritmo empieza en la raíz y visita todos los hijos antes de pasar al siguiente nivel. Este recorrido por niveles refleja las relaciones jerárquicas de los árboles: cada nodo tiene un padre y varios hijos, lo que da lugar a un patrón predecible.

En cambio, los grafos pueden contener ciclos. Múltiples caminos entre nodos pueden llevar de vuelta a nodos visitados anteriormente. Esto puede ser un problema para la BFS, ya que requiere una gestión cuidadosa de las revisitas. Llevar un registro de los nodos que se han visitado evita reprocesamientos innecesarios y ayuda a evitar ciclos que podrían causar bucles. En nuestra anterior implementación de BFS, utilizamos una lista visitada para asegurarnos de que cada nodo se procesaba sólo una vez. Si se encontraba un nodo visitado, se saltaba, lo que permitía a BFS continuar sin problemas.

Complejidad temporal y espacial

¿Cuál es la eficacia de la búsqueda amplia? Podemos utilizar la notación Big O para evaluar cómo cambia la eficiencia de BFS en función del tamaño del grafo. 

Complejidad temporal

La complejidad temporal del BFS es O(V+E), donde V es el número de vértices (nodos) y E es el número de aristas del grafo. Esto significa que el rendimiento de BFS depende tanto del número de nodos como de las conexiones entre ellos.

Complejidad espacial

La complejidad espacial de BFS es O(V) debido a la memoria necesaria para almacenar los nodos en la cola. En grafos más amplios, esto puede significar almacenar muchos nodos a la vez. En el peor de los casos, puede significar retener todos los nodos a la vez.

Aplicaciones reales de la búsqueda amplia primero

La búsqueda exhaustiva tiene numerosas aplicaciones prácticas en campos como la informática, las redes y la inteligencia artificial. Su exploración metódica nivel a nivel lo hace ideal para problemas de búsqueda y localización de caminos.

Casos prácticos

Una aplicación del BFS es en los algoritmos de encaminamiento de redes. Cuando los paquetes de datos atraviesan una red, los encaminadores utilizan BFS para encontrar el camino más corto. Al explorar todos los nodos vecinos antes de profundizar, el BFS identifica rápidamente las rutas eficientes, minimizando la latencia y mejorando el rendimiento.

El BFS también es útil para resolver puzzles, como laberintos o rompecabezas deslizantes. Cada posición es un nodo, y las conexiones son aristas. BFS puede encontrar eficazmente el camino más corto desde el inicio hasta la salida.

Otro uso potente es el análisis de redes sociales. El BFS ayuda a descubrir las relaciones entre los usuarios y a identificar los nodos influyentes. Puede explorar las conexiones sociales y descubrir grupos de usuarios relacionados, revelando información sobre las estructuras de la red.

Aplicaciones de la IA

El BFS también es útil en el entrenamiento de IA. Por ejemplo, puede utilizarse para buscar estados de partida en juegos como el ajedrez. Los algoritmos de IA pueden utilizar el BFS para explorar posibles movimientos nivel por nivel, evaluando los estados futuros para determinar la mejor acción, encontrando así el camino más corto hacia la victoria.

El BFS también se aplica a la robótica para la planificación de trayectorias. Permite a los robots navegar por entornos complejos cartografiando el entorno y encontrando caminos mientras evitan obstáculos.

Búsqueda amplia primero vs. Otros algoritmos de búsqueda

Comparemos el BFS con otros algoritmos de búsqueda habituales, como la búsqueda en profundidad y el algoritmo de Dijkstra.

Comparación con la búsqueda en profundidad

Tanto la búsqueda en amplitud como la búsqueda en profundidad (DFS) son algoritmos de recorrido de grafos, pero exploran los grafos de forma diferente. El BFS visita a todos los vecinos de la profundidad actual antes de profundizar más, mientras que el DFS explora un camino lo más lejos posible antes de retroceder.

BFS es excelente para encontrar el camino más corto en grafos no ponderados. Esta ventaja la hace buena para problemas como la navegación por laberintos y la creación de redes. En cambio, el DFS puede no encontrar siempre el camino más corto, pero puede ser más eficiente en términos de espacio en grafos profundos y anchos. Esto lo hace preferible para tareas como la ordenación topológica o los problemas de programación, donde se necesita un recorrido completo sin un uso excesivo de memoria.

Comparación con el algoritmo de Dijkstra

El algoritmo de Dijkstra es un algoritmo de recorrido de grafos diseñado para grafos ponderados, en los que las aristas tienen costes variables. A diferencia del BFS, que trata todas las aristas por igual, Dijkstra calcula el camino más corto basándose en los pesos de las aristas. Es muy útil para aplicaciones en las que el coste importa, como encontrar la ruta óptima teniendo en cuenta el tiempo de viaje.

Aunque Dijkstra es potente para grafos ponderados, es más complejo e intensivo computacionalmente. Dijkstra tiene una complejidad temporal de O((V+E)logV) cuando utiliza colas prioritarias, que es significativamente mayor que la complejidad temporal O(V+E) de BFS. Puedes obtener más información sobre el Algoritmo de Dijkstra en Implementación del Algoritmo de Dijkstra en Python: Un tutorial paso a paso.

Problemas potenciales

Un problema que puedes encontrar al utilizar BFS es quedarte atrapado en un ciclo. Un ciclo se produce cuando una ruta vuelve a un nodo visitado anteriormente, creando un bucle en el recorrido. Si el BFS no realiza un seguimiento adecuado de los nodos visitados, puede provocar un bucle infinito. Es importante mantener una lista de los nodos visitados o marcar cada nodo como explorado una vez procesado. Este sencillo enfoque debería garantizar que tu BFS explore el grafo de forma eficiente y termine correctamente.

Otro escollo frecuente es el uso incorrecto de las colas. BFS depende de una cola para llevar la cuenta de los nodos que hay que explorar. Si la cola no se gestiona correctamente, pueden faltar nodos o producirse rutas incorrectas en el recorrido. Para evitarlo, añade nodos a la cola en el orden en que deban ser explorados y luego elimínalos. Esto ayuda a BFS a explorar los nodos nivel por nivel, como se pretende. Utilizar una estructura de datos fiable, como collections.deque en Python, ayuda.

Cuándo no utilizar BFS

A pesar de su versatilidad, la BFS no es la mejor opción en todas las situaciones. Por un lado, el BFS no siempre es adecuado para grafos muy grandes o profundos, en los que puede ser más práctica la búsqueda en profundidad. Además, el BFS no es apropiado para grafos ponderados, porque el BFS trata todas las aristas por igual. Algoritmos como el de Dijkstra o el A* son más adecuados para estos casos, ya que tienen en cuenta los distintos costes al calcular el camino más corto.

Conclusión

El BFS es especialmente valioso para encontrar el camino más corto en grafos no ponderados. Su exploración por niveles la convierte en una herramienta excelente para situaciones que requieren una exploración exhaustiva de los nodos en cada nivel de profundidad.

Si te interesan los algoritmos de búsqueda, no dejes de consultar mis otros artículos de esta serie, incluidos: Búsqueda binaria en Python: Guía completa para una búsqueda eficaz. También te puede interesar Árbol AVL: Guía Completa Con Implementación En Python, e Introducción al Análisis de Redes en Python.