Breadth-First Search en Python : Un guide avec des exemples

Imaginez que vous essayez de tracer l'itinéraire le plus rapide dans un labyrinthe, d'identifier les liens entre les personnes d'un réseau social ou de trouver le moyen le plus efficace de transmettre des données sur l'internet. Ces défis ont un objectif commun : explorer systématiquement les relations entre différents points. L'algorithme de recherche "Breadth-first" peut vous aider à atteindre cet objectif.

La recherche de type "Breadth-first" est appliquée à un large éventail de problèmes dans le domaine de la science des données, allant de la traversée de graphes à la recherche de chemins. Il est particulièrement utile pour trouver le chemin le plus court dans les graphes non pondérés. Continuez à lire et je vais couvrir la recherche breadth-first en détail et montrer une implémentation en Python. Si, au moment de commencer, vous souhaitez obtenir davantage d'aide en Python, inscrivez-vous à notre cours très complet d'introduction à Python .

Qu'est-ce que la recherche en profondeur ?

Breadth-first search (BFS) est un algorithme de parcours de graphe qui explore un graphe ou un arbre niveau par niveau. À partir d'un nœud source spécifié, BFS visite tous ses voisins immédiats avant de passer au niveau de nœuds suivant. Cela permet de s'assurer que les nœuds situés à la même profondeur sont traités avant d'aller plus loin. Pour cette raison, BFS est utile pour les problèmes qui nécessitent l'examen de tous les chemins possibles de manière structurée et systématique.

BFS est utile pour trouver le chemin le plus court entre les nœuds, car la première fois que BFS atteint un nœud, il utilise le chemin le plus court. Cela rend BFS utile pour des problèmes tels que le routage de réseau, où l'objectif est de trouver l'itinéraire le plus efficace entre deux points. Le diagramme ci-dessous présente une explication simplifiée de la manière dont BFS explore un arbre.

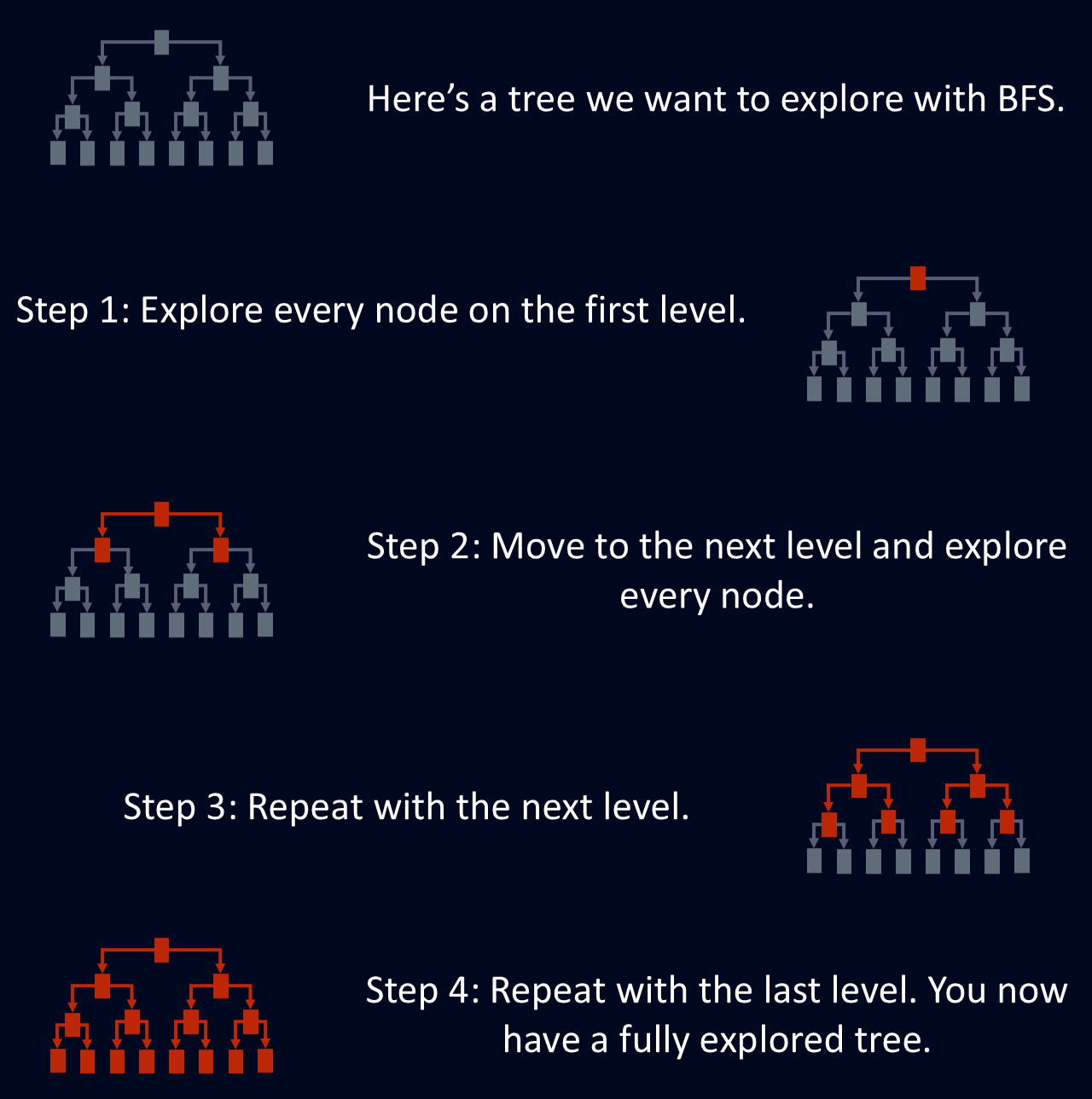
Principales caractéristiques de l'algorithme de recherche Breadth-First

La recherche en profondeur est conçue pour explorer un graphe ou un arbre en visitant tous les voisins d'un nœud avant de passer à la couche suivante. Ce parcours structuré permet de s'assurer que tous les nœuds situés à une certaine profondeur sont explorés avant d'aller plus loin dans la structure. Cette approche niveau par niveau fait de BFS un moyen systématique et fiable de naviguer dans des réseaux complexes.

Méthode d'interrogation

BFS explore chaque nœud au niveau de profondeur actuel avant de passer au suivant. Cela signifie que tous les nœuds situés à une distance donnée du point de départ sont traités avant d'aller plus loin.

Mise en œuvre basée sur les files d'attente

BFS utilise une file d'attente pour gérer les nœuds qui doivent être visités. L'algorithme traite un nœud, ajoute ses voisins non visités à la file d'attente et continue ainsi. La file d'attente fonctionne selon le principe du premier entré, premier sorti, ce qui garantit que les nœuds sont explorés dans l'ordre où ils sont découverts.

Garantie du plus court chemin dans les graphes non pondérés

Dans les graphes non pondérés, ou les graphes où chaque lien a la même longueur, BFS garantit la recherche du chemin le plus court entre les nœuds. Étant donné que BFS explore les voisins niveau par niveau, la première fois qu'il atteint un nœud, il le fait par le chemin le plus court possible. Cela rend BFS particulièrement efficace pour résoudre les problèmes du chemin le plus court, dans les situations où toutes les arêtes ont le même poids.

Applicable aux graphes et aux arbres

BFS fonctionne avec des graphes et des arbres. Un graphe est un réseau de nœuds connectés qui peuvent avoir des cycles, comme un réseau social, tandis qu'un arbre est une hiérarchie avec une racine et sans cycles, comme un pedigree. Le BFS est utile dans les deux cas, ce qui le rend applicable à un large éventail de tâches.

Implémentation de la recherche en largeur (Breadth-First Search) en Python

Démontrons l'algorithme de recherche en première intention sur un arbre en Python. Si vous avez besoin de rafraîchir vos compétences en Python, consultez le cursus de programmation Python à DataCamp. Pour plus d'informations sur les différentes structures de données et les algorithmes, suivez notre cours Structures de données et algorithmes en Python et lisez notre Structures de données : Un guide complet avec des exemples en Python tutorial.

Commençons. Tout d'abord, nous devons mettre en place un arbre de décision simple pour notre recherche BFS.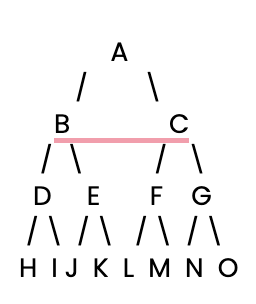

Ensuite, nous allons définir cet arbre de décision simple à l'aide d'un dictionnaire Python, où chaque clé est un nœud et sa valeur est une liste des enfants du nœud.

# Define the decision tree as a dictionary
tree = {
    'A': ['B', 'C'],  # Node A connects to B and C
    'B': ['D', 'E'],  # Node B connects to D and E
    'C': ['F', 'G'],  # Node C connects to F and G
    'D': ['H', 'I'],  # Node D connects to H and I
    'E': ['J', 'K'],  # Node E connects to J and K
    'F': ['L', 'M'],  # Node F connects to L and M
    'G': ['N', 'O'],  # Node G connects to N and O
    'H': [], 'I': [], 'J': [], 'K': [],  # Leaf nodes have no children
    'L': [], 'M': [], 'N': [], 'O': []   # Leaf nodes have no children
}

Mettons maintenant en œuvre l'algorithme BFS en Python. BFS fonctionne en visitant tous les nœuds du niveau actuel avant de passer au niveau suivant. Nous utiliserons une file d'attente pour gérer les nœuds à visiter ensuite.

from collections import deque  # Import deque for efficient queue operations

# Define the BFS function
def bfs(tree, start):
    visited = []  # List to keep track of visited nodes
    queue = deque([start])  # Initialize the queue with the starting node

    while queue:  # While there are still nodes to process
        node = queue.popleft()  # Dequeue a node from the front of the queue

        if node not in visited:  # Check if the node has been visited
            visited.append(node)  # Mark the node as visited
            print(node, end=" ")  # Output the visited node

            # Enqueue all unvisited neighbors (children) of the current node
            for neighbor in tree[node]:
                if neighbor not in visited:
                    queue.append(neighbor)  # Add unvisited neighbors to the queue

Maintenant que nous avons créé notre fonction BFS, nous pouvons l'exécuter sur l'arbre, en commençant par le nœud racine A.

# Execute BFS starting from node 'A'
bfs(tree, 'A')

Lorsque nous l'exécutons, il affiche chaque nœud dans l'ordre dans lequel il a été visité.

A B C D E F G H I J K L M N O

BFS sur les arbres vs. Graphiques

Le modèle de traversée de BFS est direct dans les arbres, puisqu'ils sont intrinsèquement acycliques. L'algorithme commence à la racine et visite tous les enfants avant de passer au niveau suivant. Cette traversée des niveaux reflète les relations hiérarchiques des arbres : chaque nœud a un parent et plusieurs enfants, ce qui donne lieu à un schéma prévisible.

En revanche, les graphes peuvent contenir des cycles. Plusieurs chemins entre les nœuds peuvent mener à des nœuds visités précédemment. Cela peut être un problème pour le BFS, qui nécessite une gestion prudente des revisites. Le cursus des nœuds visités permet d'éviter les retraitements inutiles et les cycles susceptibles de provoquer des boucles. Dans notre précédente implémentation de BFS, nous avons utilisé une liste de visites pour nous assurer que chaque nœud n'était traité qu'une seule fois. Si un nœud visité était rencontré, il était ignoré, ce qui permettait à BFS de continuer sans heurts.

Complexité du temps et de l'espace

Quelle est l'efficacité de la recherche de type "breadth-first" ? Nous pouvons utiliser la notation Big O pour évaluer l'évolution de l'efficacité de BFS en fonction de la taille du graphe. 

Complexité temporelle

La complexité temporelle de BFS est O(V+E), où V est le nombre de sommets (nœuds) et E le nombre d'arêtes du graphe. Cela signifie que les performances de BFS dépendent à la fois du nombre de nœuds et des connexions entre eux.

Complexité de l'espace

La complexité spatiale de BFS est O(V) en raison de la mémoire nécessaire pour stocker les nœuds dans la file d'attente. Dans les graphes plus larges, cela peut signifier qu'il faut stocker de nombreux nœuds à la fois. Dans le pire des cas, cela peut signifier qu'il faut tenir tous les nœuds en même temps.

Applications concrètes de la recherche en profondeur (Breadth-First Search)

La recherche en profondeur a de nombreuses applications pratiques dans des domaines tels que l'informatique, les réseaux et l'intelligence artificielle. Son exploration méthodique niveau par niveau en fait un outil idéal pour les problèmes de recherche et d'orientation.

Cas d'utilisation

Les algorithmes de routage des réseaux constituent l'une des applications de la méthode BFS. Lorsque des paquets de données traversent un réseau, les routeurs utilisent BFS pour trouver le chemin le plus court. En explorant tous les nœuds voisins avant d'aller plus loin, BFS identifie rapidement les itinéraires efficaces, minimisant ainsi la latence et améliorant les performances.

Le BFS est également utile pour résoudre des puzzles, comme les labyrinthes ou les puzzles à glissière. Chaque position est un nœud et les connexions sont des arêtes. BFS permet de trouver efficacement le chemin le plus court entre le point de départ et le point d'arrivée.

L'analyse des réseaux sociaux constitue une autre utilisation efficace. BFS permet de découvrir les relations entre les utilisateurs et d'identifier les nœuds influents. Il permet d'explorer les connexions sociales et de découvrir des groupes d'utilisateurs apparentés, révélant ainsi des informations sur les structures des réseaux.

Applications de l'IA

Le BFS est également utile pour la formation à l'IA. Par exemple, il peut être utilisé pour rechercher des états de jeu dans des jeux tels que les échecs. Les algorithmes d'IA peuvent utiliser BFS pour explorer les mouvements possibles niveau par niveau, en évaluant les états futurs pour déterminer la meilleure action, et ainsi trouver le chemin le plus court vers la victoire.

Le BFS est également appliqué à la robotique pour la planification de trajectoires. Il permet aux robots de naviguer dans des environnements complexes en cartographiant les environs et en trouvant des chemins tout en évitant les obstacles.

Recherche en largeur d'abord et recherche en profondeur ensuite. Autres algorithmes de recherche

Comparons BFS à d'autres algorithmes de recherche courants, tels que la recherche en profondeur d'abord et l'algorithme de Dijkstra.

Comparaison avec la recherche en profondeur

La recherche en largeur et la recherche en profondeur sont toutes deux des algorithmes de parcours de graphes, mais elles explorent les graphes différemment. BFS visite tous les voisins à la profondeur actuelle avant d'aller plus loin, tandis que DFS explore un chemin aussi loin que possible avant de revenir sur ses pas.

BFS est idéal pour trouver le chemin le plus court dans les graphes non pondérés. Cet avantage lui permet de résoudre des problèmes tels que la navigation dans les labyrinthes et la mise en réseau. En revanche, DFS ne trouve pas toujours le chemin le plus court, mais il peut être plus efficace en termes d'espace dans les graphes larges et profonds. Il est donc préférable pour des tâches telles que le tri topologique ou les problèmes d'ordonnancement, où une traversée complète est nécessaire sans utilisation excessive de la mémoire.

Comparaison avec l'algorithme de Dijkstra

L'algorithme de Dijkstra est un algorithme de traversée de graphe conçu pour les graphes pondérés, où les arêtes ont des coûts variables. Contrairement à BFS, qui traite toutes les arêtes de la même manière, Dijkstra calcule le chemin le plus court en fonction du poids des arêtes. Il est particulièrement utile pour les applications où le coût est important, par exemple pour trouver l'itinéraire optimal en tenant compte de la durée du trajet.

Bien que Dijkstra soit puissant pour les graphes pondérés, il est plus complexe et nécessite plus de calculs. Dijkstra a une complexité temporelle de O((V+E)logV) lorsqu'il utilise des files d'attente prioritaires, ce qui est nettement plus élevé que la complexité temporelle de BFS, qui est de O(V+E). Pour en savoir plus sur l'algorithme de Dijkstra, consultez le site Implementing the Dijkstra Algorithm in Python : Un tutoriel étape par étape.

Problèmes potentiels

L'un des problèmes que vous pouvez rencontrer lorsque vous utilisez BFS est de vous retrouver pris dans un cycle. Un cycle se produit lorsqu'un chemin revient à un nœud précédemment visité, créant ainsi une boucle dans la traversée. Si BFS ne suit pas correctement les nœuds visités, cela peut conduire à une boucle infinie. Il est important de conserver une liste des nœuds visités ou de marquer chaque nœud comme exploré une fois qu'il a été traité. Cette approche simple devrait permettre à votre BFS d'explorer efficacement le graphe et de se terminer correctement.

Un autre écueil fréquent est l'utilisation incorrecte des files d'attente. Le système BFS repose sur une file d'attente qui permet de savoir quels nœuds doivent être explorés. Si la file d'attente n'est pas gérée correctement, des nœuds manquants ou des chemins incorrects peuvent apparaître lors de la traversée. Pour éviter cela, ajoutez les nœuds à la file d'attente dans l'ordre où ils doivent être explorés, puis retirez-les. Cela permet à BFS d'explorer les nœuds niveau par niveau, comme prévu. L'utilisation d'une structure de données fiable, comme collections.deque dans Python, est utile.

Quand ne pas utiliser le BFS

Malgré sa polyvalence, le BFS n'est pas le meilleur choix dans toutes les situations. D'une part, BFS n'est pas toujours adapté aux graphes très grands ou très profonds, où la recherche en profondeur d'abord peut être plus pratique. En outre, BFS n'est pas approprié pour les graphes pondérés, car il traite toutes les arêtes de la même manière. Les algorithmes tels que Dijkstra ou A* sont mieux adaptés à ces cas, car ils tiennent compte des différents coûts lors du calcul du chemin le plus court.

Conclusion

BFS est particulièrement utile pour trouver le chemin le plus court dans les graphes non pondérés. Son exploration par niveau en fait un excellent outil pour les situations qui nécessitent une exploration approfondie des nœuds à chaque niveau de profondeur.

Si vous vous intéressez aux algorithmes de recherche, n'oubliez pas de consulter les autres articles de cette série, notamment : Recherche binaire en Python : Un guide complet pour une recherche efficace. Vous pouvez également être intéressé par AVL Tree : Complete Guide With Python Implementation, et Introduction à l'analyse des réseaux en Python.