Breadth-First Search em Python: Um guia com exemplos

Imagine que você esteja tentando mapear a rota mais rápida em um labirinto, identificar conexões entre pessoas em uma rede social ou encontrar a maneira mais eficiente de transmitir dados pela Internet. Esses desafios têm um objetivo em comum: explorar sistematicamente as relações entre diferentes pontos. A pesquisa Breadth-first é um algoritmo que pode ajudar você a fazer exatamente isso.

A busca ampla e prioritária é aplicada a uma ampla gama de problemas na ciência de dados, desde a passagem de gráficos até a busca de caminhos. Ele é particularmente útil para encontrar o caminho mais curto em gráficos não ponderados. Se você continuar lendo, abordarei a pesquisa de amplitude em primeiro lugar em detalhes e mostrarei uma implementação em Python. Se, ao começarmos, você quiser mais ajuda com Python, inscreva-se em nosso curso abrangente de Introdução ao Python .

O que é a pesquisa Breadth-First?

O Breadth-first search (BFS) é um algoritmo de passagem de gráfico que explora um gráfico ou uma árvore nível por nível. A partir de um nó de origem especificado, o BFS visita todos os seus vizinhos imediatos antes de passar para o próximo nível de nós. Isso garante que os nós na mesma profundidade sejam processados antes de se aprofundar. Por esse motivo, o BFS é útil para problemas que exigem o exame de todos os caminhos possíveis de forma estruturada e sistemática.

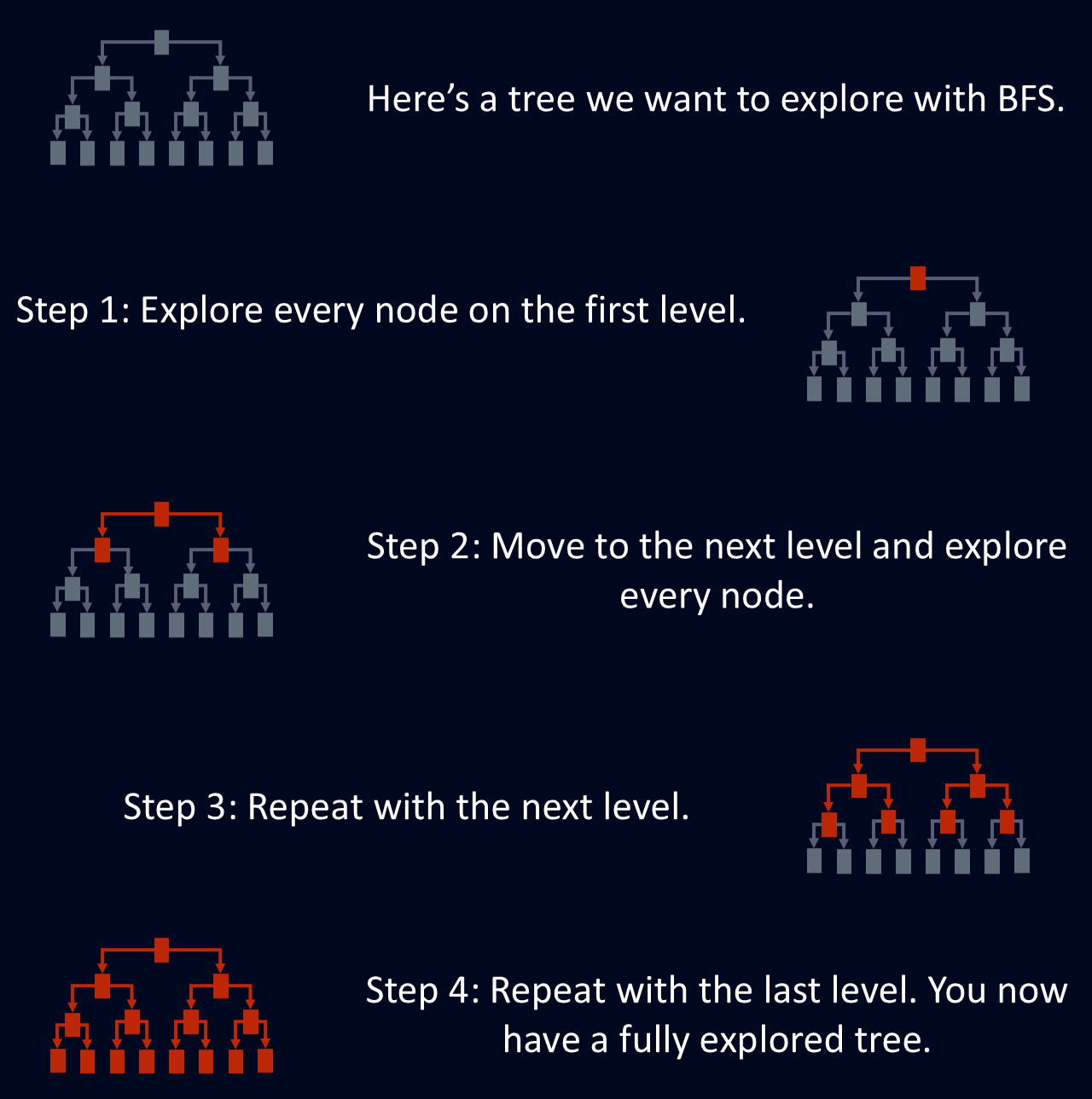
O BFS é útil para encontrar o caminho mais curto entre os nós, porque na primeira vez que o BFS chega a um nó, ele usa a rota mais curta. Isso torna o BFS útil para problemas como roteamento de rede, em que o objetivo é encontrar a rota mais eficiente entre dois pontos. O diagrama abaixo mostra uma explicação simplificada de como o BFS explora uma árvore.

Principais recursos do algoritmo de pesquisa Breadth-First

A pesquisa de amplitude em primeiro lugar foi projetada para explorar um gráfico ou uma árvore visitando todos os vizinhos de um nó antes de avançar para a próxima camada. Essa travessia estruturada garante que todos os nós em uma determinada profundidade sejam explorados antes de você se aprofundar na estrutura. Essa abordagem de nível por nível torna o BFS uma maneira sistemática e confiável de navegar em redes complexas.

Método de travessia

O BFS explora cada nó no nível de profundidade atual antes de passar para o próximo. Isso significa que todos os nós a uma determinada distância do ponto inicial são processados antes de se aprofundarem.

Implementação baseada em filas

O BFS usa uma fila para gerenciar os nós que precisam ser visitados. O algoritmo processa um nó, adiciona seus vizinhos não visitados à fila e continua esse padrão. A fila opera de acordo com o princípio "primeiro a entrar, primeiro a sair", garantindo que os nós sejam explorados na ordem em que são descobertos.

Caminho mais curto garantido em gráficos não ponderados

Em gráficos não ponderados, ou gráficos em que cada link tem o mesmo comprimento, o BFS garante que você encontre o caminho mais curto entre os nós. Como o BFS explora os vizinhos nível por nível, na primeira vez que chega a um nó, ele o faz por meio da rota mais curta possível. Isso torna o BFS especialmente eficaz para resolver problemas de caminho mais curto, em situações em que todas as bordas têm o mesmo peso.

Aplicável a gráficos e árvores

O BFS funciona com gráficos e árvores. Um gráfico é uma rede de nós conectados que podem ter ciclos, como uma rede social, enquanto uma árvore é uma hierarquia com uma raiz e sem ciclos, como um pedigree. O BFS é útil para ambos, o que o torna amplamente aplicável a uma grande variedade de tarefas.

Implementação da pesquisa Breadth-First em Python

Vamos demonstrar o algoritmo de pesquisa de amplitude em primeiro lugar em uma árvore em Python. Se você precisa atualizar suas habilidades em Python, confira o curso de habilidades em programação Python no DataCamp. Para obter mais informações sobre diferentes estruturas de dados e algoritmos, faça nosso curso Estruturas de dados e algoritmos em Python e leia nosso Estruturas de dados: Um guia abrangente com exemplos em Python tutorial.

Vamos começar. Primeiro, precisamos configurar uma árvore de decisão simples para o nosso BFS pesquisar.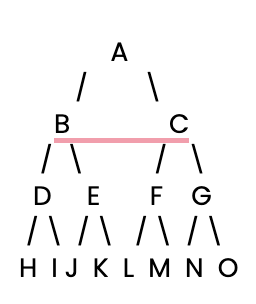

Em seguida, definiremos essa árvore de decisão simples usando um dicionário Python, em que cada chave é um nó e seu valor é uma lista dos filhos do nó.

# Define the decision tree as a dictionary
tree = {
    'A': ['B', 'C'],  # Node A connects to B and C
    'B': ['D', 'E'],  # Node B connects to D and E
    'C': ['F', 'G'],  # Node C connects to F and G
    'D': ['H', 'I'],  # Node D connects to H and I
    'E': ['J', 'K'],  # Node E connects to J and K
    'F': ['L', 'M'],  # Node F connects to L and M
    'G': ['N', 'O'],  # Node G connects to N and O
    'H': [], 'I': [], 'J': [], 'K': [],  # Leaf nodes have no children
    'L': [], 'M': [], 'N': [], 'O': []   # Leaf nodes have no children
}

Agora vamos implementar o algoritmo BFS em Python. O BFS funciona visitando todos os nós no nível atual antes de passar para o próximo nível. Usaremos uma fila para gerenciar quais nós serão visitados em seguida.

from collections import deque  # Import deque for efficient queue operations

# Define the BFS function
def bfs(tree, start):
    visited = []  # List to keep track of visited nodes
    queue = deque([start])  # Initialize the queue with the starting node

    while queue:  # While there are still nodes to process
        node = queue.popleft()  # Dequeue a node from the front of the queue

        if node not in visited:  # Check if the node has been visited
            visited.append(node)  # Mark the node as visited
            print(node, end=" ")  # Output the visited node

            # Enqueue all unvisited neighbors (children) of the current node
            for neighbor in tree[node]:
                if neighbor not in visited:
                    queue.append(neighbor)  # Add unvisited neighbors to the queue

Agora que criamos nossa função BFS, podemos executá-la na árvore, começando pelo nó raiz A.

# Execute BFS starting from node 'A'
bfs(tree, 'A')

Quando você executa esse procedimento, ele gera cada nó na ordem em que foi visitado.

A B C D E F G H I J K L M N O

BFS em árvores vs. Gráficos

O padrão de passagem do BFS é simples em árvores, pois elas são inerentemente acíclicas. O algoritmo começa na raiz e visita todos os filhos antes de passar para o próximo nível. Essa passagem de ordem de nível reflete as relações hierárquicas nas árvores: cada nó tem um pai e vários filhos, o que leva a um padrão previsível.

Por outro lado, os gráficos podem conter ciclos. Vários caminhos entre nós podem levar de volta a nós visitados anteriormente. Isso pode ser um problema para o BFS, exigindo um gerenciamento cuidadoso das revisitas. Manter o controle de quais nós foram visitados impede o reprocessamento desnecessário e ajuda a evitar ciclos que poderiam causar loops. Em nossa implementação anterior do BFS, usamos uma lista de visitas para garantir que cada nó fosse processado apenas uma vez. Se um nó visitado fosse encontrado, ele era ignorado, permitindo que o BFS continuasse sem problemas.

Complexidade de tempo e espaço

Qual é a eficiência da pesquisa de amplitude em primeiro lugar? Podemos usar a notação Big O para avaliar como a eficiência do BFS muda em função do tamanho do gráfico. 

Complexidade de tempo

A complexidade de tempo do BFS é O(V+E), em que V é o número de vértices (nós) e E é o número de arestas no gráfico. Isso significa que o desempenho do BFS depende tanto do número de nós quanto das conexões entre eles.

Complexidade espacial

A complexidade espacial do BFS é O(V) devido à memória necessária para armazenar os nós na fila. Em gráficos mais amplos, isso pode significar o armazenamento de muitos nós de uma só vez. Na pior das hipóteses, isso pode significar manter todos os nós ao mesmo tempo.

Aplicativos do mundo real da pesquisa Breadth-First

A busca ampla e prioritária tem inúmeras aplicações práticas em áreas como ciência da computação, redes e inteligência artificial. Sua exploração metódica nível a nível o torna ideal para problemas de busca e localização de caminhos.

Casos de uso

Uma aplicação do BFS é em algoritmos de roteamento de rede. Quando os pacotes de dados atravessam uma rede, os roteadores usam o BFS para encontrar o caminho mais curto. Ao explorar todos os nós vizinhos antes de se aprofundar, o BFS identifica rapidamente rotas eficientes, minimizando a latência e melhorando o desempenho.

O BFS também é útil para resolver quebra-cabeças, como labirintos ou quebra-cabeças deslizantes. Cada posição é um nó, e as conexões são bordas. O BFS pode encontrar com eficiência o caminho mais curto desde o início até a saída.

Outro uso poderoso é a análise de redes sociais. O BFS ajuda a descobrir relacionamentos entre usuários e a identificar nós influentes. Ele pode explorar conexões sociais e descobrir grupos de usuários relacionados, revelando insights sobre estruturas de rede.

Aplicativos de IA

O BFS também é útil no treinamento de IA. Por exemplo, ele pode ser usado para pesquisar estados de jogo em jogos como xadrez. Os algoritmos de IA podem usar o BFS para explorar os movimentos possíveis nível por nível, avaliando os estados futuros para determinar a melhor ação e, assim, encontrar o caminho mais curto para a vitória.

O BFS também é aplicado à robótica para planejamento de caminhos. Ele permite que os robôs naveguem em ambientes complexos mapeando os arredores e encontrando caminhos enquanto evitam obstáculos.

Pesquisa de amplitude versus pesquisa de largura. Outros algoritmos de pesquisa

Vamos comparar o BFS com outros algoritmos de busca comuns, como a busca em profundidade e o algoritmo de Dijkstra.

Comparação com a busca em profundidade

A busca em largura (Breadth-first search) e a busca em profundidade (DFS) são algoritmos de passagem de gráficos, mas exploram os gráficos de forma diferente. O BFS visita todos os vizinhos na profundidade atual antes de se aprofundar, enquanto o DFS explora o máximo possível de um caminho antes de voltar atrás.

O BFS é excelente para encontrar o caminho mais curto em gráficos não ponderados. Essa vantagem faz com que ele seja bom para problemas como navegação em labirintos e redes. Por outro lado, o DFS pode nem sempre encontrar o caminho mais curto, mas pode ser mais eficiente em termos de espaço em gráficos amplos e profundos. Isso o torna preferível para tarefas como classificação topológica ou problemas de agendamento, em que uma passagem completa é necessária sem uso excessivo de memória.

Comparação com o algoritmo de Dijkstra

O algoritmo de Dijkstra é um algoritmo de travessia de gráfico projetado para gráficos ponderados, em que as bordas têm custos variáveis. Ao contrário do BFS, que trata todas as bordas igualmente, o Dijkstra calcula o caminho mais curto com base nos pesos das bordas. É mais útil para aplicativos em que o custo é importante, como encontrar a rota ideal considerando o tempo de viagem.

Embora o Dijkstra seja eficiente para gráficos ponderados, ele é mais complexo e exige mais recursos computacionais. Dijkstra tem uma complexidade de tempo de O((V+E)logV) ao usar filas de prioridade, que é significativamente maior do que a complexidade de tempo O(V+E) do BFS. Você pode saber mais sobre o Algoritmo de Dijkstra em Implementando o Algoritmo de Dijkstra em Python: Um tutorial passo a passo.

Problemas em potencial

Um problema que você pode encontrar ao usar o BFS é ficar preso em um ciclo. Um ciclo ocorre quando um caminho retorna a um nó visitado anteriormente, criando um loop na travessia. Se o BFS não rastrear corretamente os nós visitados, isso pode levar a um loop infinito. É importante manter uma lista de nós visitados ou marcar cada nó como explorado depois de processado. Essa abordagem simples deve garantir que seu BFS explore o gráfico de forma eficiente e termine corretamente.

Outra armadilha comum é o uso incorreto da fila. O BFS depende de uma fila para manter o controle de quais nós precisam ser explorados. Se a fila não for gerenciada adequadamente, isso pode resultar em nós ausentes ou caminhos incorretos na passagem. Para evitar isso, adicione nós à fila na ordem em que eles precisam ser explorados e, em seguida, remova-os. Isso ajuda o BFS a explorar os nós nível por nível, conforme pretendido. O uso de uma estrutura de dados confiável, como collections.deque em Python, ajuda.

Quando não usar o BFS

Apesar de sua versatilidade, o BFS não é a melhor opção em todas as situações. Por um lado, o BFS nem sempre é adequado para gráficos muito grandes ou profundos, nos quais a busca em profundidade pode ser mais prática. Além disso, o BFS não é adequado para gráficos ponderados, pois trata todas as bordas da mesma forma. Algoritmos como o de Dijkstra ou o A* são mais adequados para esses casos, pois levam em conta os custos variáveis ao calcular o caminho mais curto.

Conclusão

O BFS é particularmente valioso para encontrar o caminho mais curto em gráficos não ponderados. Sua exploração por níveis o torna uma excelente ferramenta para situações que exigem uma exploração completa dos nós em cada nível de profundidade.

Se você tiver interesse em algoritmos de pesquisa, não deixe de conferir meus outros artigos desta série, incluindo: Pesquisa binária em Python: Um guia completo para uma pesquisa eficiente. Você também pode estar interessado em AVL Tree: Complete Guide With Python Implementation, e Introduction to Network Analysis in Python.