Breadth-First Search in Python: Ein Leitfaden mit Beispielen

Stell dir vor, du versuchst, den schnellsten Weg durch ein Labyrinth zu finden, Verbindungen zwischen Menschen in einem sozialen Netzwerk zu identifizieren oder den effizientesten Weg zur Datenübertragung im Internet zu finden. Diese Herausforderungen haben ein gemeinsames Ziel: die systematische Erforschung von Beziehungen zwischen verschiedenen Punkten. Die Breadth-First-Suche ist ein Algorithmus, der dir dabei helfen kann, genau das zu tun.

Die Breadth-First-Suche wird für eine Vielzahl von Problemen in der Datenwissenschaft eingesetzt, von der Graphenüberquerung bis zur Pfadfindung. Sie ist besonders nützlich, um den kürzesten Weg in ungewichteten Graphen zu finden. Lies weiter und ich werde die Breadth-First-Suche im Detail behandeln und eine Implementierung in Python zeigen. Wenn du zu Beginn mehr Hilfe in Python brauchst, melde dich für unseren umfassenden Kurs Einführung in Python an.

Was ist Breadth-First Search?

Breadth-first search (BFS) ist ein Graph-Traversal-Algorithmus, der einen Graphen oder Baum Ebene für Ebene erkundet. Ausgehend von einem bestimmten Ursprungsknoten besucht BFS alle seine unmittelbaren Nachbarn, bevor es zur nächsten Ebene von Knoten weitergeht. Dadurch wird sichergestellt, dass die Knoten in der gleichen Tiefe bearbeitet werden, bevor sie tiefer gehen. Deshalb ist BFS nützlich für Probleme, bei denen alle möglichen Pfade auf strukturierte, systematische Weise untersucht werden müssen.

BFS ist nützlich, um den kürzesten Weg zwischen Knotenpunkten zu finden, denn wenn BFS einen Knotenpunkt zum ersten Mal erreicht, verwendet es die kürzeste Route. Das macht BFS nützlich für Probleme wie Netzwerk-Routing, bei dem es darum geht, die effizienteste Route zwischen zwei Punkten zu finden. Das folgende Diagramm zeigt eine vereinfachte Erklärung, wie BFS einen Baum erkundet.

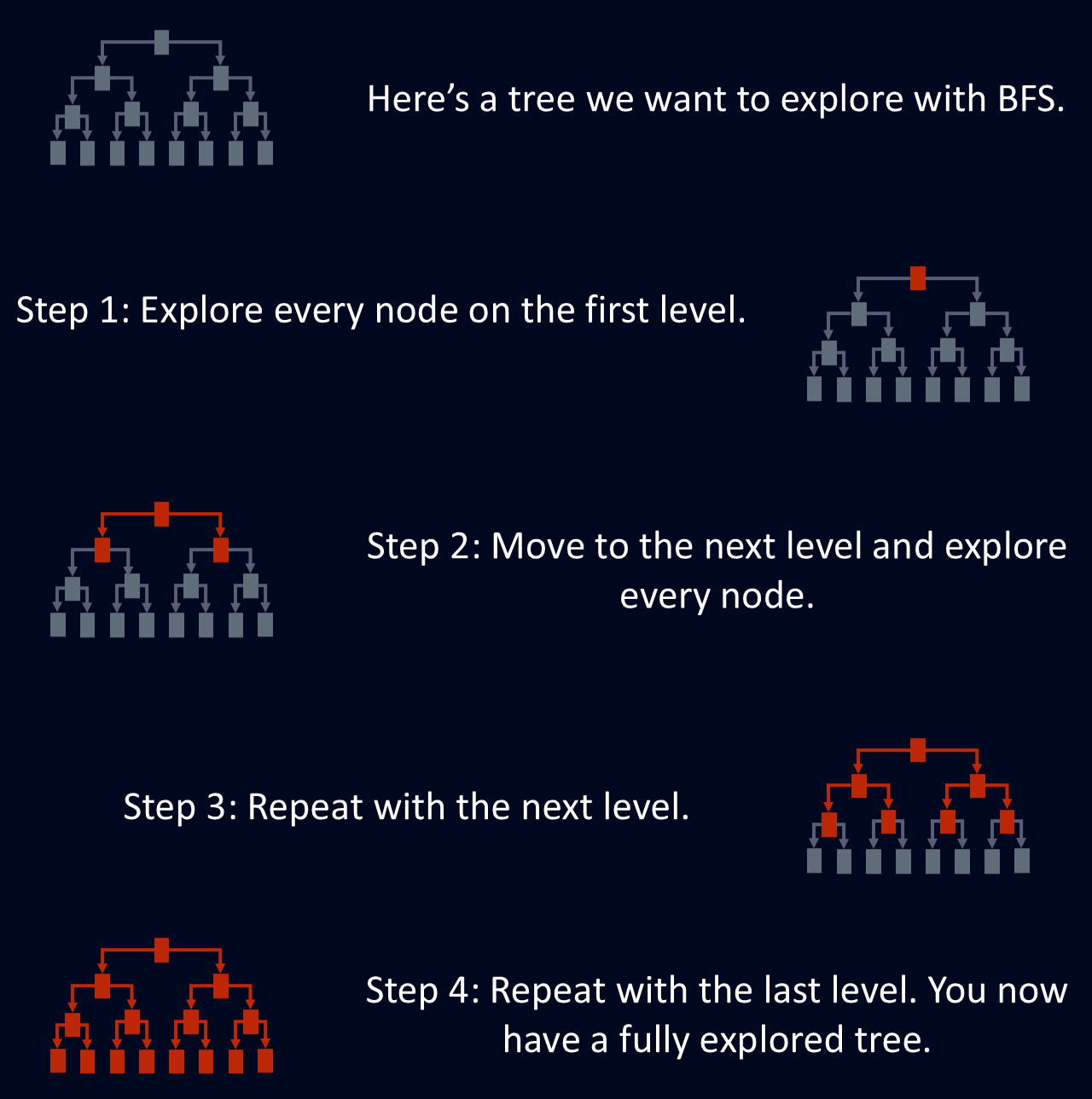
Hauptmerkmale des Breadth-First-Suchalgorithmus

Die Breadth-First-Suche wurde entwickelt, um einen Graphen oder Baum zu erkunden, indem alle Nachbarn eines Knotens besucht werden, bevor die nächste Ebene erreicht wird. Dieses strukturierte Traversieren stellt sicher, dass alle Knoten in einer bestimmten Tiefe erforscht werden, bevor man tiefer in die Struktur eindringt. Dieser stufenweise Ansatz macht BFS zu einem systematischen und zuverlässigen Weg, sich in komplexen Netzwerken zurechtzufinden.

Traversal-Methode

BFS untersucht jeden Knoten auf der aktuellen Tiefenstufe, bevor es zum nächsten weitergeht. Das bedeutet, dass alle Knoten, die sich in einer bestimmten Entfernung vom Startpunkt befinden, abgearbeitet werden, bevor sie weitergehen.

Warteschlangenbasierte Implementierung

BFS verwendet eine Warteschlange, um Knotenpunkte zu verwalten, die besucht werden müssen. Der Algorithmus verarbeitet einen Knoten, fügt seine nicht besuchten Nachbarn zur Warteschlange hinzu und setzt dieses Muster fort. Die Warteschlange arbeitet nach dem Prinzip "first-in, first-out" und stellt sicher, dass die Knoten in der Reihenfolge erkundet werden, in der sie entdeckt werden.

Garantiert kürzester Weg in ungewichteten Graphen

In ungewichteten Graphen oder Graphen, in denen jede Verbindung gleich lang ist, garantiert BFS das Finden des kürzesten Weges zwischen den Knoten. Da das BFS die Nachbarn Ebene für Ebene erkundet, erreicht es einen Knotenpunkt beim ersten Mal über die kürzeste Route. Das macht BFS besonders effektiv bei der Lösung von Problemen mit kürzesten Wegen, bei denen alle Kanten gleich viel Gewicht haben.

Anwendbar sowohl auf Graphen als auch auf Bäume

BFS funktioniert sowohl mit Graphen als auch mit Bäumen. Ein Graph ist ein Netzwerk aus verbundenen Knoten, das Zyklen haben kann, wie ein soziales Netzwerk, während ein Baum eine Hierarchie mit einer Wurzel und ohne Zyklen ist, wie ein Stammbaum. BFS eignet sich für beides und ist damit für eine Vielzahl von Aufgaben einsetzbar.

Die Implementierung der Breadth-First-Suche in Python

Lass uns den Breadth-First-Suchalgorithmus für einen Baum in Python demonstrieren. Wenn du deine Python-Kenntnisse auffrischen möchtest, solltest du dir den Lernpfad Python-Programmierung auf dem DataCamp ansehen. Für weitere Informationen über verschiedene Datenstrukturen und Algorithmen, belege unseren Kurs Datenstrukturen und Algorithmen in Python und lies unseren Datenstrukturen: Ein umfassendes Handbuch mit Python-Beispielen tutorial.

Lass uns loslegen. Zunächst müssen wir einen einfachen Entscheidungsbaum für unser BFS erstellen.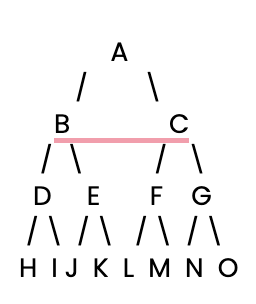

Als Nächstes definieren wir diesen einfachen Entscheidungsbaum mit Hilfe eines Python-Wörterbuchs, in dem jeder Schlüssel ein Knoten ist und sein Wert eine Liste der Kinder des Knotens ist.

# Define the decision tree as a dictionary
tree = {
    'A': ['B', 'C'],  # Node A connects to B and C
    'B': ['D', 'E'],  # Node B connects to D and E
    'C': ['F', 'G'],  # Node C connects to F and G
    'D': ['H', 'I'],  # Node D connects to H and I
    'E': ['J', 'K'],  # Node E connects to J and K
    'F': ['L', 'M'],  # Node F connects to L and M
    'G': ['N', 'O'],  # Node G connects to N and O
    'H': [], 'I': [], 'J': [], 'K': [],  # Leaf nodes have no children
    'L': [], 'M': [], 'N': [], 'O': []   # Leaf nodes have no children
}

Jetzt wollen wir den BFS-Algorithmus in Python implementieren. BFS funktioniert, indem alle Knoten auf der aktuellen Ebene besucht werden, bevor die nächste Ebene erreicht wird. Wir verwenden eine Warteschlange, um zu verwalten, welche Knoten als Nächstes besucht werden sollen.

from collections import deque  # Import deque for efficient queue operations

# Define the BFS function
def bfs(tree, start):
    visited = []  # List to keep track of visited nodes
    queue = deque([start])  # Initialize the queue with the starting node

    while queue:  # While there are still nodes to process
        node = queue.popleft()  # Dequeue a node from the front of the queue

        if node not in visited:  # Check if the node has been visited
            visited.append(node)  # Mark the node as visited
            print(node, end=" ")  # Output the visited node

            # Enqueue all unvisited neighbors (children) of the current node
            for neighbor in tree[node]:
                if neighbor not in visited:
                    queue.append(neighbor)  # Add unvisited neighbors to the queue

Jetzt, wo wir unsere BFS-Funktion erstellt haben, können wir sie auf dem Baum ausführen, beginnend mit dem Wurzelknoten A.

# Execute BFS starting from node 'A'
bfs(tree, 'A')

Wenn wir dies ausführen, wird jeder Knoten in der Reihenfolge ausgegeben, in der er besucht wurde.

A B C D E F G H I J K L M N O

BFS auf Bäumen vs. Diagramme

Das Traversalmuster von BFS ist bei Bäumen einfach, da sie von Natur aus azyklisch sind. Der Algorithmus beginnt bei der Wurzel und besucht alle Kinder, bevor er zur nächsten Ebene übergeht. Dieses Durchlaufen der Ebenen spiegelt die hierarchischen Beziehungen in Bäumen wider: Jeder Knoten hat ein Elternteil und mehrere Kinder, was zu einem vorhersehbaren Muster führt.

Im Gegensatz dazu können Graphen Zyklen enthalten. Mehrere Pfade zwischen Knotenpunkten können zu zuvor besuchten Knotenpunkten zurückführen. Das kann für BFS ein Problem sein und erfordert ein sorgfältiges Management der Wiederholungsbesuche. Durch die Verfolgung der besuchten Knotenpunkte werden unnötige Wiederholungen vermieden und Zyklen, die zu Schleifen führen könnten, verhindert. In unserer früheren BFS-Implementierung haben wir eine Besuchsliste verwendet, um sicherzustellen, dass jeder Knoten nur einmal bearbeitet wurde. Wenn ein besuchter Knotenpunkt angetroffen wurde, wurde er übersprungen, sodass das BFS reibungslos fortgesetzt werden konnte.

Zeit und Raum Komplexität

Wie effizient ist die Breadth-First-Suche? Wir können die Big O-Notation verwenden, um zu bewerten, wie sich die Effizienz von BFS in Abhängigkeit von der Graphengröße verändert. 

Zeitliche Komplexität

Die Zeitkomplexität von BFS ist O(V+E), wobei V die Anzahl der Eckpunkte (Knoten) und E die Anzahl der Kanten im Graphen ist. Das bedeutet, dass die Leistung von BFS sowohl von der Anzahl der Knotenpunkte als auch von den Verbindungen zwischen ihnen abhängt.

Raumkomplexität

Die Raumkomplexität von BFS ist O(V), da der Speicher für die Speicherung der Knoten in der Warteschlange benötigt wird. In größeren Graphen kann dies bedeuten, dass viele Knoten auf einmal gespeichert werden. Im schlimmsten Fall kann es bedeuten, dass jeder Knotenpunkt auf einmal gehalten wird.

Praktische Anwendungen der Breadth-First-Suche

Die Breadth-First-Suche hat zahlreiche praktische Anwendungen in Bereichen wie Informatik, Netzwerke und künstliche Intelligenz. Die methodische Erkundung von Ebene zu Ebene macht sie ideal für Such- und Wegfindungsprobleme.

Anwendungsfälle

Eine Anwendung von BFS ist der Routing-Algorithmus für Netzwerke. Wenn Datenpakete ein Netzwerk durchqueren, verwenden Router BFS, um den kürzesten Weg zu finden. Durch die Erkundung aller Nachbarknoten, bevor es in die Tiefe geht, findet das BFS schnell effiziente Routen, minimiert die Latenzzeit und verbessert die Leistung.

BFS ist auch nützlich, um Rätsel wie Labyrinthe oder Schiebepuzzles zu lösen. Jede Position ist ein Knoten und die Verbindungen sind Kanten. BFS kann den kürzesten Weg vom Start zum Ziel effizient finden.

Eine weitere wichtige Anwendung ist die Analyse sozialer Netzwerke. BFS hilft dabei, Beziehungen zwischen Nutzern zu entdecken und einflussreiche Knotenpunkte zu identifizieren. Es kann soziale Verbindungen erforschen und Cluster verwandter Nutzerinnen und Nutzer entdecken, die Einblicke in die Netzwerkstrukturen gewähren.

KI-Anwendungen

BFS ist auch beim KI-Training nützlich. Sie kann zum Beispiel für die Suche nach Spielständen in Spielen wie Schach verwendet werden. KI-Algorithmen können BFS nutzen, um mögliche Züge Level für Level zu erkunden und zukünftige Zustände zu bewerten, um die beste Aktion zu bestimmen und so den kürzesten Weg zum Sieg zu finden.

BFS wird auch in der Robotik zur Bahnplanung eingesetzt. Sie ermöglicht es Robotern, sich in komplexen Umgebungen zurechtzufinden, indem sie die Umgebung kartieren, Wege finden und Hindernissen ausweichen.

Breadth-First-Suche vs. Andere Suchalgorithmen

Vergleichen wir BFS mit anderen gängigen Suchalgorithmen, wie z.B. der Deep-First-Suche und dem Dijkstra-Algorithmus.

Vergleich mit Depth-First-Suche

Die Breadth-First-Suche und die Depth-First-Suche (DFS) sind beides Algorithmen zur Durchquerung von Graphen, aber sie untersuchen Graphen auf unterschiedliche Weise. BFS besucht alle Nachbarn in der aktuellen Tiefe, bevor es tiefer geht, während DFS einen Pfad so weit wie möglich erkundet, bevor es zurückgeht.

BFS eignet sich hervorragend, um den kürzesten Weg in ungewichteten Graphen zu finden. Dieser Vorteil macht es gut für Probleme wie Labyrinthnavigation und Vernetzung. Im Gegensatz dazu findet das DFS nicht immer den kürzesten Weg, aber es kann in tiefen, breiten Graphen platzsparender sein. Das macht es für Aufgaben wie topologische Sortierung oder Scheduling-Probleme, bei denen ein komplettes Traversal ohne übermäßigen Speicherverbrauch benötigt wird, besser geeignet.

Vergleich mit Dijkstra's Algorithmus

Der Dijkstra-Algorithmus ist ein Algorithmus zur Durchquerung von Graphen, der für gewichtete Graphen entwickelt wurde, in denen die Kanten unterschiedliche Kosten haben. Im Gegensatz zu BFS, bei dem alle Kanten gleich behandelt werden, berechnet Dijkstra den kürzesten Weg anhand der Kantengewichte. Sie ist besonders nützlich für Anwendungen, bei denen die Kosten eine Rolle spielen, z. B. bei der Suche nach der optimalen Route unter Berücksichtigung der Reisezeit.

Dijkstra ist zwar leistungsstark für gewichtete Graphen, aber komplexer und rechenintensiver. Dijkstra hat eine Zeitkomplexität von O((V+E)logV), wenn er Prioritätswarteschlangen verwendet, was deutlich höher ist als die Zeitkomplexität von BFS O(V+E). Mehr über Dijkstras Algorithmus erfährst du unter Implementing the Dijkstra Algorithm in Python: Ein Schritt-für-Schritt-Tutorial.

Mögliche Probleme

Ein Problem, auf das du bei der Verwendung von BFS stoßen kannst, ist, dass du in einen Kreislauf gerätst. Ein Zyklus entsteht, wenn ein Pfad zu einem zuvor besuchten Knoten zurückkehrt und so eine Schleife im Traversal bildet. Wenn das BFS die besuchten Knoten nicht richtig verfolgt, kann dies zu einer Endlosschleife führen. Es ist wichtig, eine Liste der besuchten Knoten zu führen oder jeden Knoten nach der Bearbeitung als erforscht zu markieren. Dieser einfache Ansatz sollte sicherstellen, dass dein BFS den Graphen effizient erforscht und ordnungsgemäß beendet.

Ein weiterer häufiger Fallstrick ist die falsche Verwendung von Warteschlangen. BFS ist auf einen Lernpfad angewiesen, um zu wissen, welche Knoten erkundet werden müssen. Wenn die Warteschlange nicht richtig verwaltet wird, kann das zu fehlenden Knoten oder falschen Pfaden beim Traversal führen. Um dies zu vermeiden, fügst du die Knoten in der Reihenfolge, in der sie erkundet werden müssen, zur Warteschlange hinzu und entfernst sie dann. Das hilft dem BFS, die Knoten wie beabsichtigt Ebene für Ebene zu erkunden. Die Verwendung einer zuverlässigen Datenstruktur, wie collections.deque in Python, hilft dabei.

Wann du BFS nicht verwenden solltest

Trotz seiner Vielseitigkeit ist das BFS nicht in jeder Situation die beste Wahl. Zum einen ist BFS nicht immer für sehr große oder tiefe Graphen geeignet, in denen die Tiefensuche praktischer sein kann. Außerdem ist BFS nicht für gewichtete Graphen geeignet, weil BFS alle Kanten gleich behandelt. Algorithmen wie Dijkstra oder A* sind für diese Fälle besser geeignet, da sie bei der Berechnung des kürzesten Weges die unterschiedlichen Kosten berücksichtigen.

Fazit

BFS ist besonders nützlich, um den kürzesten Weg in ungewichteten Graphen zu finden. Seine stufenweise Erkundung macht es zu einem ausgezeichneten Werkzeug für Situationen, die eine gründliche Erkundung der Knoten auf jeder Tiefenstufe erfordern.

Wenn du dich für Suchalgorithmen interessierst, solltest du dir auch meine anderen Artikel in dieser Reihe ansehen, z. B: Binäre Suche in Python: Ein kompletter Leitfaden für eine effiziente Suche. Das könnte dich auch interessieren: AVL Tree: Complete Guide With Python Implementation, und Introduction to Network Analysis in Python.