Grados de libertad: Definición, significado y ejemplos

Los grados de libertad son uno de esos términos estadísticos que a menudo suenan abstractos o confusos al principio. Es posible que ya hayas oído este término en algún libro de texto.

La respuesta breve es que los grados de libertad miden cuánta libertad tienen tus datos para variar una vez que se imponen ciertas restricciones, como una media o un total fijos. Si esto te parece confuso, no te preocupes: En este artículo, a partir de la siguiente sección, lo explicaré con detalle. Explicaré por qué existen y daré ejemplos claros para que puedas estudiarlos y desarrollar una intuición rigurosa.

¿Qué se entiende por grados de libertad?

Los grados de libertad representan el número de valores de un conjunto de datos o cálculo que pueden variar libremente una vez que se han tenido en cuenta todas las restricciones.

Imagina que te piden que elijas tres números cuya suma sea exactamente 30.  Puedes elegir libremente los dos primeros números, pero el tercero se fija automáticamente para que el total sea 30. Esto reduce el número de valores que realmente pueden variar libremente. Por lo tanto, los grados de libertad nos indican cuántos datos independientes quedan después de aplicar las restricciones.

Cómo hallar los grados de libertad

En general, los grados de libertad se calculan como el número de observaciones n menos el número de restricciones o parámetros estimados a partir de los datos.

Las diferentes pruebas estadísticas aplican diferentes restricciones, lo que explica que las fórmulas varíen, como en el caso de n-1 para una prueba t de una sola muestra. En la práctica, rara vez es necesario calcular los grados de libertad manualmente, ya que los programas estadísticos lo hacen automáticamente. Sin embargo, comprender el principio general te ayudará inevitablemente a interpretar los resultados correctamente.

Por qué los grados de libertad son importantes en estadística

Los grados de libertad existen porque los cálculos estadísticos dependen en gran medida de estimaciones, como la media o la varianza muestral, que consumen la información de los datos. Por lo tanto, sin tener en cuenta estas limitaciones, nuestras estimaciones de variabilidad, intervalos de confianza, valores p y otros serían inexactas.

En términos generales, un mayor grado de libertad conduce predominantemente a estimaciones más precisas e intervalos de confianza más estrechos. También aparecen en la comprobación de hipótesis porque determinan qué distribución utilizar y cuánta información tiene la prueba. Por lo tanto, esto afecta directamente a la fiabilidad de la inferencia estadística.

Grados de libertad explicados con un ejemplo sencillo

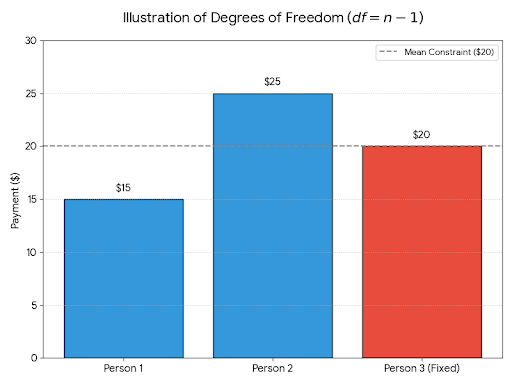
Supongamos que tienes tres amigos que están dividiendo una cuenta de restaurante de 60 dólares. Quieres que el pago medio sea de 20 $ por persona, así que sigues los siguientes pasos:

1. Tú eliges libremente el primer pago de 15 $.
2. Tú eliges libremente el segundo pago de 25 $.
3. El tercer pago debe ser de 20 dólares para que la media sea de 20 dólares, lo que da un total de 60 dólares.

Así que, aunque tienes tres valores e, solo dos podían variar libremente. Decimos que el último fue determinado por la restricción (que es la media fija). Por lo tanto, los grados de libertad aquí son iguales a 3-1=2.

Esto muestra que el número de puntos de datos (3) no es igual a los grados de libertad (2). Decimos que la restricción consume un grado de libertad.

Grados de libertad en pruebas estadísticas comunes

En esta sección, mostraré algunos ejemplos de grados de libertad en pruebas estadísticas comunes y cómo utilizarlos.

Grados de libertad en una prueba t

Para una prueba t de una muestra, los grados de libertad = n - 1. En este caso, se utiliza un grado de libertad porque estimamos la media muestral a partir de los datos. Para un tamaño de muestra mayor, se obtiene un df más alto con pruebas t más fiables.

Grados de libertad en las pruebas de chi cuadrado

En una prueba de bondad de ajuste chi-cuadrado, los grados de libertad = número de categorías - 1. Por lo tanto, la restricción es que la frecuencia total observada debe ser igual a la frecuencia total esperada.

Grados de libertad en ANOVA

En el ANOVA unidireccional, los grados de libertad se dividen entre grupos (k-1, donde k es el número de grupos) y dentro de los grupos (N-k, donde N = tamaño total de la muestra). Esto muestra las restricciones tanto de las medias de los grupos como de la media global del conjunto de datos.

Conceptos erróneos comunes sobre los grados de libertad

En esta sección, abordaré algunas de las ideas más erróneas sobre los grados de libertad. En primer lugar, los grados de libertad no son el tamaño de la muestra, ya que los grados de libertad suelen ser menores debido a las restricciones que los reducen. 

En otras palabras, los grados de libertad no son lo mismo que el número de variables o parámetros. Contáis específicamente las piezas de información independientes después de las restricciones.

Además, un mayor grado de libertad no siempre es mejor, y siempre hay que sopesar las ventajas y los inconvenientes, ya que un grado de libertad muy elevado puede indicar un sobreajuste o supuestos poco realistas en algunos contextos.

Grados de libertad frente a Tamaño de la muestra

El tamaño de la muestra n es el número total de observaciones. Aunque los grados de libertad no son exactamente el tamaño de la muestra, están muy influenciados por él. Esto se debe a que los grados de libertad suelen ser n menos el número de restricciones o parámetros estimados. Esta es la razón por la que df es casi siempre menor que n. La relación entre ellos existe porque la estimación de los parámetros impone restricciones a los datos.

Cómo interpretar los grados de libertad

La regla general es centrarse menos en el cálculo exacto y más en lo que realmente representa la restricción.

Un bajo grado de libertad implica menos datos independientes, lo que a su vez conduce a intervalos de confianza más amplios y a una menor potencia estadística. Debes confiar en los resultados de tu software, pero siempre realiza comprobaciones de coherencia, como preguntarte si los grados de libertad indicados tienen sentido teniendo en cuenta el tamaño de la muestra y la prueba que se está realizando.

Conclusión

Los grados de libertad miden la cantidad de información verdaderamente independiente disponible en tus datos después de tener en cuenta todas las restricciones. La idea principal que hay que tener en cuenta es sencilla: cada vez que estimas un parámetro o impones una restricción, pierdes un grado de libertad. Por lo tanto, comprender este concepto refuerza tu intuición estadística y te ayuda a interpretar los resultados de las pruebas con mayor confianza. Con la práctica, los grados de libertad te resultarán mucho menos misteriosos y mucho más significativos.