Degrés de liberté : Définition, signification et exemples

Les degrés de liberté sont l'un de ces termes statistiques qui peuvent sembler abstraits ou confus au premier abord. Vous avez peut-être déjà rencontré ce terme dans un manuel scolaire.

En résumé, les degrés de liberté mesurent le degré de liberté dont disposent vos données pour varier une fois que certaines restrictions, telles qu'une moyenne ou un total fixe, sont imposées. Si cela vous semble confus, ne vous inquiétez pas : Dans cet article, à partir de la section suivante, je vais développer ce sujet en détail. Je vais vous expliquer leur raison d'être et vous fournir des exemples clairs afin que vous puissiez les étudier et développer une intuition rigoureuse.

Que signifie « degrés de liberté » ?

Les degrés de liberté représentent le nombre de valeurs dans un ensemble de données ou un calcul qui peuvent varier librement une fois que toutes les contraintes ont été prises en compte.

Imaginez qu'on vous demande de choisir trois nombres dont la somme est exactement égale à 30.  Vous pouvez choisir librement les deux premiers chiffres, mais le troisième chiffre est automatiquement fixé pour que le total soit égal à 30. Cela réduit le nombre de valeurs qui peuvent réellement varier librement. Par conséquent, les degrés de liberté nous indiquent combien d'éléments d'information indépendants subsistent après l'application des restrictions.

Comment déterminer les degrés de liberté

En général, les degrés de liberté sont calculés comme étant le nombre d'observations n moins le nombre de contraintes ou de paramètres estimés à partir des données.

Différents tests statistiques appliquent différentes contraintes, ce qui explique pourquoi les formules varient, comme dans le cas de n-1 pour un test t à échantillon unique. En pratique, il est rarement nécessaire de calculer manuellement les degrés de liberté, car les logiciels statistiques le font automatiquement. Cependant, la compréhension du principe général vous aidera inévitablement à interpréter correctement les résultats.

Pourquoi les degrés de liberté sont-ils importants en statistique ?

Les degrés de liberté existent car les calculs statistiques s'appuient fortement sur des estimations, telles que la moyenne ou la variance de l'échantillon, qui utilisent les informations contenues dans les données. Par conséquent, sans tenir compte de ces contraintes, nos estimations de variabilité, nos intervalles de confiance, nos valeurs p et autres seraient inexacts.

De manière générale, des degrés de liberté plus élevés conduisent principalement à des estimations plus précises et à des intervalles de confiance plus étroits. Ils apparaissent également dans les tests d'hypothèse, car ils déterminent la distribution à utiliser et la quantité d'informations contenues dans le test. Cela affecte donc directement la fiabilité de l'inférence statistique.

Les degrés de liberté expliqués à l'aide d'un exemple simple

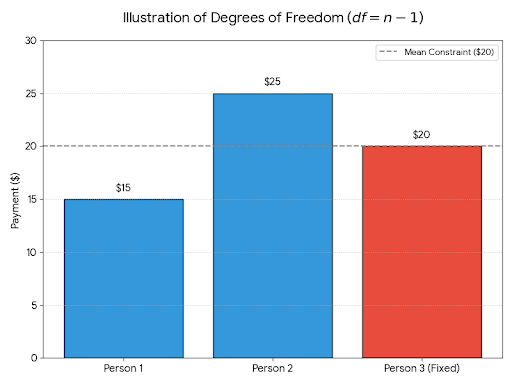
Supposons que vous ayez trois amis qui partagent une addition de restaurant de 60 $. Vous souhaitez que le paiement moyen soit de 20 $ par personne, veuillez donc suivre les étapes suivantes :

1. Vous êtes libre de choisir le premier paiement de 15 $.
2. Vous êtes libre de choisir le deuxième paiement de 25 $.
3. Le troisième paiement doit être de 20 $ pour que la moyenne soit de 20 $, ce qui donne un total de 60 $.

Ainsi, même si vous disposez de trois valeurs, seules deux d'entre elles pouvaient varier librement. Nous affirmons que le dernier a été déterminé par la contrainte (qui est la moyenne fixe). Par conséquent, les degrés de liberté sont ici égaux à 3-1=2.

Cela démontre que le nombre de points de données (3) n'est pas identique au nombre de degrés de liberté (2). Nous affirmons que la contrainte utilise un degré de liberté.

Degrés de liberté dans les tests statistiques courants

Dans cette section, je vais présenter quelques exemples de degrés de liberté dans des tests statistiques courants et expliquer comment les utiliser.

Degrés de liberté dans un test t

Pour un test t à un échantillon, les degrés de liberté sont égaux à n - 1. Dans ce cas, un degré de liberté est utilisé car nous estimons la moyenne de l'échantillon à partir des données. Pour un échantillon de plus grande taille, nous obtenons un df plus élevé avec des tests t plus fiables.

Degrés de liberté dans les tests du chi carré

Dans un test d'adéquation du chi carré, les degrés de liberté = nombre de catégories - 1. Par conséquent, la contrainte est que la fréquence totale observée doit être égale à la fréquence totale attendue.

Degrés de liberté dans l'ANOVA

Dans l'ANOVA à un facteur, les degrés de liberté sont répartis entre les groupes (k-1, où k est le nombre de groupes) et au sein des groupes (N-k, où N = taille totale de l'échantillon). Ceci illustre les contraintes liées aux moyennes des deux groupes et à la moyenne globale de l'ensemble de données.

Idées reçues courantes sur les degrés de liberté

Dans cette section, j'aborderai certaines des idées les plus erronées concernant les degrés de liberté. Tout d'abord, les degrés de liberté ne correspondent pas à la taille de l'échantillon, car ils sont généralement plus petits en raison des contraintes qui les réduisent. 

En d'autres termes, les degrés de liberté ne sont pas identiques au nombre de variables ou de paramètres. Ils comptent spécifiquement les éléments d'information indépendants après les contraintes.

De plus, un degré de liberté plus élevé n'est pas toujours préférable, et il y a toujours un compromis à faire, car un degré de liberté très élevé peut indiquer un surajustement ou des hypothèses irréalistes dans certains contextes.

Degrés de liberté par rapport à Taille de l'échantillon

La taille de l'échantillon n correspond au nombre total d'observations. Bien que les degrés de liberté ne correspondent pas exactement à la taille de l'échantillon, ils en sont fortement influencés. Cela découle du fait que les degrés de liberté sont généralement égaux à n moins le nombre de contraintes ou de paramètres estimés. C'est la raison pour laquelle df est presque toujours inférieur à n. La relation entre eux existe car l'estimation des paramètres impose des contraintes sur les données.

Comment interpréter les degrés de liberté

La règle générale consiste à se concentrer moins sur le calcul exact et davantage sur ce que la contrainte représente réellement.

Un faible degré de liberté implique moins d'informations indépendantes, ce qui conduit à des intervalles de confiance plus larges et à une puissance statistique moindre. Il est recommandé de faire confiance aux résultats fournis par votre logiciel, mais il est toujours judicieux de procéder à des vérifications, par exemple en vous demandant si les degrés de liberté indiqués sont pertinents compte tenu de la taille de votre échantillon et du test effectué.

Conclusion

Les degrés de liberté mesurent la quantité d'informations véritablement indépendantes disponibles dans vos données après avoir pris en compte toutes les contraintes. L'idée principale à retenir est simple : chaque fois que vous estimez un paramètre ou imposez une restriction, vous perdez un degré de liberté. Par conséquent, la compréhension de ce concept renforce votre intuition statistique et vous aide à interpréter les résultats des tests avec plus de confiance. Avec la pratique, les degrés de liberté vous sembleront beaucoup moins mystérieux et beaucoup plus significatifs.