Freiheitsgrade: Definition, Bedeutung und Beispiele

Freiheitsgrade sind einer dieser statistischen Begriffe, die am Anfang oft abstrakt oder verwirrend klingen. Vielleicht hast du diesen Begriff schon mal irgendwo in einem Lehrbuch gesehen.

Die kurze Antwort ist, dass Freiheitsgrade zeigen, wie viel Spielraum deine Daten haben, um sich zu verändern, wenn bestimmte Einschränkungen wie ein fester Mittelwert oder eine feste Summe festgelegt sind. Wenn das verwirrend klingt, mach dir keine Sorgen: In diesem Artikel werde ich ab dem nächsten Abschnitt genauer drauf eingehen. Ich erkläre dir, warum es sie gibt, und gebe dir klare Beispiele, damit du sie studieren und eine fundierte Intuition entwickeln kannst.

Was meinen wir mit Freiheitsgraden?

Freiheitsgrade zeigen an, wie viele Werte in einem Datensatz oder einer Berechnung frei variieren können, wenn alle Einschränkungen berücksichtigt wurden.

Stell dir vor, du sollst drei Zahlen aussuchen, die zusammen genau 30 ergeben.  Du kannst die ersten beiden Zahlen frei wählen, aber die dritte Zahl wird automatisch festgelegt, damit die Summe 30 ergibt. Dadurch wird die Anzahl der Werte reduziert, die wirklich frei variieren können. Also, Freiheitsgrade zeigen uns, wie viele unabhängige Infos übrig bleiben, nachdem die Einschränkungen angewendet wurden.

Wie man Freiheitsgrade findet

Im Allgemeinen werden Freiheitsgrade berechnet, indem man die Anzahl der Beobachtungen n von der Anzahl der Einschränkungen oder Parameter, die aus den Daten geschätzt werden, abzieht.

Verschiedene statistische Tests haben unterschiedliche Einschränkungen, deshalb sind die Formeln unterschiedlich, wie zum Beispiel bei n-1 für einen t-Test mit einer Stichprobe. In der Praxis musst du Freiheitsgrade selten manuell berechnen, weil das die Statistiksoftware automatisch macht. Das allgemeine Prinzip zu verstehen, hilft dir aber auf jeden Fall dabei, die Ergebnisse richtig zu deuten.

Warum Freiheitsgrade in der Statistik wichtig sind

Freiheitsgrade gibt's, weil statistische Berechnungen stark auf Schätzungen wie dem Stichprobenmittel oder der Varianz basieren, die die Infos aus den Daten nutzen. Ohne diese Einschränkungen zu berücksichtigen, wären unsere Schätzungen der Variabilität, Konfidenzintervalle, p-Werte und andere ungenau.

Im Allgemeinen führen mehr Freiheitsgrade meistens zu genaueren Schätzungen und engeren Konfidenzintervallen. Sie tauchen auch bei der Hypothesentestung auf, weil sie bestimmen, welche Verteilung man nimmt und wie viel Info der Test hat. Das wirkt sich direkt auf die Zuverlässigkeit der statistischen Schlussfolgerung aus.

Freiheitsgrade erklärt anhand eines einfachen Beispiels

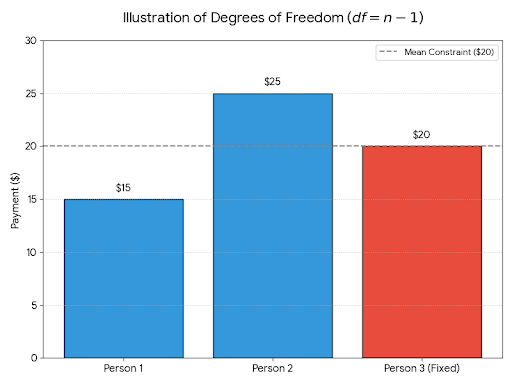
Angenommen, du hast drei Freunde, die sich eine Restaurantrechnung von 60 Dollar teilen. Du willst, dass die durchschnittliche Zahlung 20 $ pro Person beträgt, also machst du Folgendes:

1. Du kannst die erste Zahlung von 15 $ frei wählen.
2. Du kannst die zweite Zahlung von 25 Dollar frei wählen.
3. Die dritte Zahlung muss 20 Dollar betragen, damit der Durchschnitt bei 20 Dollar liegt, was insgesamt 60 Dollar ergibt.

Auch wenn du drei Werte hast, waren nur zwei frei variierbar. Wir sagen, dass der letzte durch die Einschränkung (also den festen Mittelwert) bestimmt wurde. Also sind die Freiheitsgrade hier gleich 3-1=2.

Das zeigt, dass die Anzahl der Datenpunkte (3) nicht mit den Freiheitsgraden (2) übereinstimmt. Wir sagen, dass die Einschränkung einen Freiheitsgrad verbraucht.

Freiheitsgrade in gängigen statistischen Tests

In diesem Abschnitt zeige ich dir ein paar Beispiele für Freiheitsgrade in gängigen statistischen Tests und wie man sie benutzt.

Freiheitsgrade im t-Test

Bei einem t-Test für eine Stichprobe sind die Freiheitsgrade = n - 1. In diesem Fall wird ein Freiheitsgrad verbraucht, weil wir den Stichprobenmittelwert aus den Daten schätzen. Bei einer größeren Stichprobengröße kriegen wir einen höheren Freiheitsgrad mit zuverlässigeren t-Tests.

Freiheitsgrade in Chi-Quadrat-Tests

Bei einem Chi-Quadrat-Anpassungstest ist die Anzahl der Freiheitsgrade gleich der Anzahl der Kategorien minus 1. Die Einschränkung ist also, dass die Gesamtzahl der beobachteten Häufigkeiten der Gesamtzahl der erwarteten Häufigkeiten entsprechen muss.

Freiheitsgrade in der ANOVA

Bei der einseitigen ANOVA werden die Freiheitsgrade zwischen den Gruppen (k-1, wobei k die Anzahl der Gruppen ist) und innerhalb der Gruppen (N-k, wobei N die Gesamtstichprobengröße ist) aufgeteilt. Das zeigt die Einschränkungen sowohl der Gruppenmittelwerte als auch des Gesamtmittelwerts des Datensatzes.

Häufige Irrtümer über Freiheitsgrade

In diesem Abschnitt werde ich auf einige der häufigsten Missverständnisse zum Thema Freiheitsgrade eingehen. Zuerst mal sind die Freiheitsgrade nicht die Stichprobengröße, weil die Freiheitsgrade normalerweise kleiner sind, weil es Einschränkungen gibt, die sie verringern. 

Also, Freiheitsgrade sind nicht dasselbe wie die Anzahl der Variablen oder Parameter. Sie zählen genau die einzelnen Infos nach den Einschränkungen.

Außerdem sind mehr Freiheitsgrade nicht immer besser, und es gibt immer einen Kompromiss, weil sehr viele Freiheitsgrade in manchen Fällen auf Überanpassung oder unrealistische Annahmen hindeuten können.

Freiheitsgrade vs. Stichprobengröße

Die Stichprobengröße n ist die Gesamtzahl der Beobachtungen. Die Freiheitsgrade sind zwar nicht genau die Stichprobengröße, werden aber stark davon beeinflusst. Das kommt daher, dass die Freiheitsgrade normalerweise n minus der Anzahl der Einschränkungen oder geschätzten Parameter sind. Deshalb ist df fast immer kleiner als n. Die Beziehung zwischen ihnen besteht, weil die Schätzung der Parameter den Daten Einschränkungen auferlegt.

Wie man Freiheitsgrade versteht

Die Faustregel ist, sich weniger auf die genaue Berechnung zu konzentrieren, sondern mehr darauf, was die Einschränkung eigentlich bedeutet.

Weniger Freiheitsgrade bedeuten weniger unabhängige Infos, was dann zu größeren Konfidenzintervallen und weniger statistischer Aussagekraft führt. Du solltest den Ergebnissen deiner Software vertrauen, aber immer mal nachschauen, ob die gemeldeten Freiheitsgrade bei deiner Stichprobengröße und dem durchgeführten Test Sinn machen.

Fazit

Die Freiheitsgrade zeigen an, wie viel wirklich unabhängige Infos in deinen Daten verfügbar sind, nachdem alle Einschränkungen berücksichtigt wurden. Der wichtigste Gedanke, den du dir merken solltest, ist einfach: Jedes Mal, wenn du einen Parameter schätzt oder eine Einschränkung machst, verlierst du einen Freiheitsgrad. Wenn du dieses Konzept verstehst, stärkt das deine statistische Intuition und hilft dir, Testergebnisse mit größerer Sicherheit zu interpretieren. Mit etwas Übung werden Freiheitsgrade viel weniger geheimnisvoll und viel bedeutungsvoller wirken.