Ecuación característica: Todo lo que necesitas saber para la Ciencia de Datos

Con el crecimiento exponencial de la disponibilidad de datos y las técnicas de aprendizaje automático, el álgebra lineal ha encontrado un lugar fundamental en las matemáticas del aprendizaje automático y la ciencia de datos. Como tal, los aspirantes a científicos de datos y aprendizaje automático se beneficiarán enormemente del aprendizaje de los conceptos fundamentales del álgebra lineal, incluidos los vectores y las matrices, sus propiedades y las operaciones comunes que se les aplican.

Te animo a que sigas nuestro curso de Álgebra Lineal para la Ciencia de Datos en R para desarrollar una sólida base matemática para la ciencia de datos y el aprendizaje automático. Al cursar esta asignatura, llegarás a apreciar el álgebra lineal como una materia bella e interesante que implica la síntesis del álgebra y la geometría (a través de rectas, planos y volúmenes). En concreto, verás cómo los datos de alta dimensión son muy adecuados para ser representados en forma de objetos vectoriales (por ejemplo, texto, imágenes, audio y características), y verás cómo estos objetos matemáticos como vectores tienen amplias aplicaciones en ciencia e ingeniería, como la física, la estadística y la informática.

En este artículo, examinaremos detenidamente uno de los objetos fundamentales del álgebra lineal llamado matriz. Como otros objetos matemáticos, las matrices tienen algunos atributos que las caracterizan. En concreto, repasaré y presentaré un atributo caracterizador de una matriz cuadrada: el polinomio característico o ecuación característica. Echemos un vistazo.

Definición de la ecuación característica

Un polinomio es una función con incógnitas de potencia n. La incógnita se muestra generalmente mediante la letra x, pero en casos de uso especial, se utiliza una notación diferente, como la letra griega 𝝀 (lambda), que utilizaremos en nuestra notación. El polinomio característico de una matriz cuadrada A ∈Rn× n y la incógnita 𝝀 se define como:

Donde det(.) es el determinante de una matriz cuadrada y I es la matriz identidad.

Cuando fijamos este polinomio característico igual a cero (para resolver para 𝝀), la llamamos ecuación característica. Las raíces de esta ecuación polinómica se denominan valores propios, que son conceptos importantes en la transformación de matrices y el aprendizaje automático (por ejemplo, la reducción de la dimensionalidad). Si tienes dudas sobre los vectores propios y los valores propios, tenemos un tutorial sobre el tema: Vectores y valores propios: Ideas clave para la ciencia de datos.

Derivación y cálculo de la ecuación característica

Mostramos cómo se formula un polinomio característico para una matriz cuadrada 2x2, donde

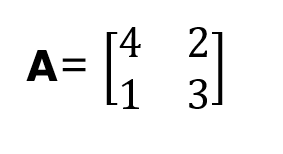
A partir de la definición de polinomio característico, tenemos:

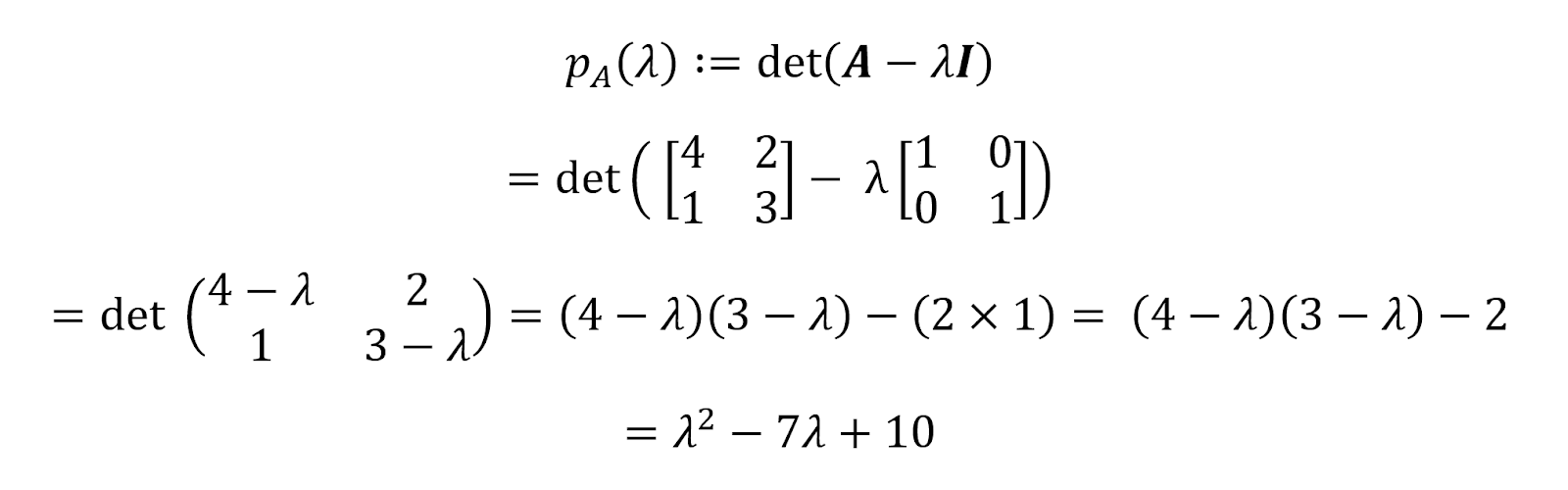
Por tanto, el polinomio característico de la matriz A anterior es p_A(𝝀)=𝝀2-7𝝀+10. Podemos hallar las raíces de este polinomio igualándolo a cero.

Utilizar la ecuación característica para hallar valores y vectores propios

Un polinomio característico de una matriz cuadrada contiene características importantes sobre su matriz asociada, incluidos los valores propios y el determinante. Por tanto, es posible extraer los valores propios de un polinomio característico resolviendo la incógnita. Anteriormente ilustramos el proceso de hallar los valores propios a partir del polinomio característico de una matriz cuadrada A de 2x2. Como hemos demostrado, el polinomio característico de esta matriz es:

Ahora, para hallar el(los) valor(es) propio(s), igualamos este polinomio a cero y hallamos las raíces utilizando métodos algebraicos (o computacionales):

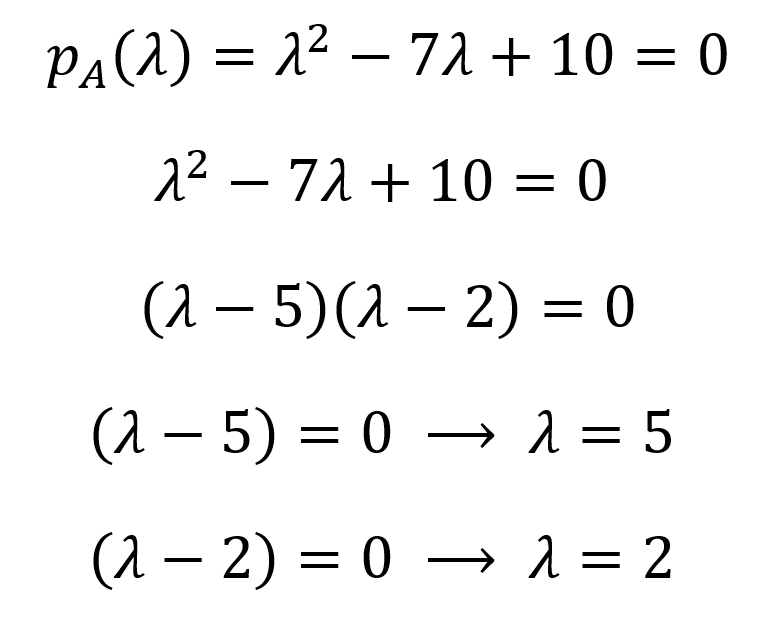
Por tanto, los valores propios son 𝝀₁=5 y 𝝀₂=2 (los valores propios se enumeran convencionalmente en orden decreciente, ya que implican la cantidad de información de determinadas matrices de datos). El conjunto de todos los valores propios de una matriz se denomina espectro propio o espectro de dicha matriz. A partir de los valores propios, podemos deducir los vectores propios de una matriz en el espacio nulo utilizando (A-𝝀I)x=0 para cada valor propio:

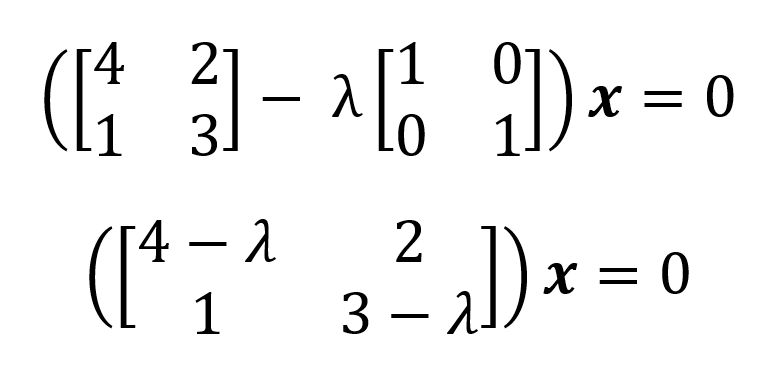
Para𝝀₁=5 introducimos 5 y resolvemos el sistema homogéneo de ecuaciones:

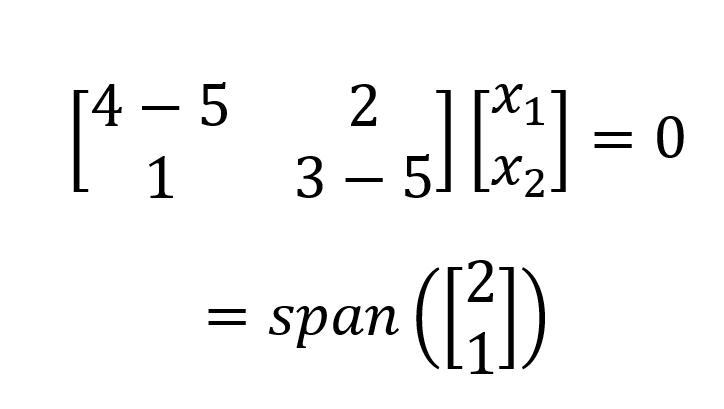
Lo que da un eigespacio unidimensional (es decir, un vector base). Realizamos el mismo proceso para 𝝀₂=2 y obtenemos

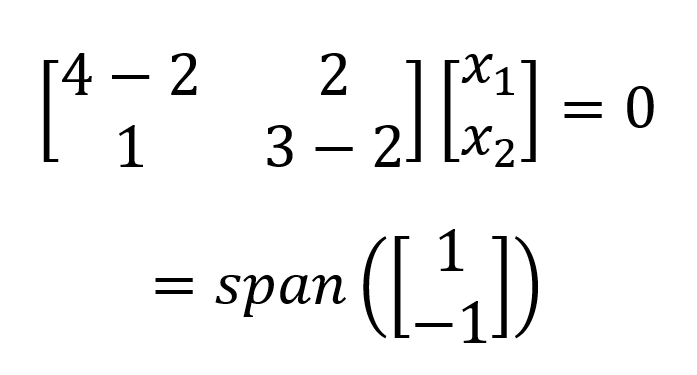
En este ejemplo, tenemos dos valores propios distintos. Una matriz también puede tener varios valores propios idénticos repetidos, lo que da un espacio propio multidimensional (es decir, varios vectores base). En este caso, la dimensionalidad del espacio propio abarcado por los distintos vectores propios se denomina multiplicidad geométrica del valor propio i.

Por otra parte, el número de veces que se repite un valor propio de una matriz se denomina multiplicidad algebraica. Probablemente, una de las aplicaciones más interesantes de los valores y vectores propios es el algoritmo PageRank que Google utiliza para la clasificación por importancia de los resultados de las búsquedas. Nuestro curso Predictive Analytics using Networked Data in R tiene un interesante capítulo sobre el algoritmo PageRank, por si te interesa. 

Técnicas computacionales

Un polinomio característico es, de hecho, un polinomio matemático con propiedades especiales (por ejemplo, incluye la traza, el determinante y los valores propios de una matriz cuadrada). Por ello, encontrar las raíces de la ecuación característica se vuelve engorroso con grados n más altos. 

Además, derivar el polinomio característico requiere que calcules el determinante de la matriz cuadrada. Aunque por razones pedagógicas, proporcionamos un ejemplo y un método para derivar y resolver el polinomio característico sobre papel y a mano, en las aplicaciones reales de la ciencia de datos, se utilizan métodos numéricos (computacionales) para calcular o aproximar las raíces de un polinomio característico. La expansión de Laplace, la eliminación de Gauss y las descomposiciones QR son algunos métodos que permiten hallar numéricamente los determinantes. 

Para hallar las raíces del polinomio característico, los algoritmos habituales son el método de Newton-Raphson, la bisección, el método de la secante y el método de Muller.

Aplicaciones de la ecuación característica

Los valores propios y los vectores propios son características matemáticas fundamentales de las matrices que pueden derivarse de una ecuación característica de una matriz cuadrada. En estadística y aprendizaje automático, las ecuaciones características se utilizan para distintos algoritmos que se basan en los valores propios y que se utilizan para algoritmos de reducción de datos y extracción de información, como por ejemplo

• Análisis de Componentes Principales (ACP) y la reducción de la dimensionalidad, en la que un conjunto de datos se reduce a un número menor de vectores basándose en los valores de los valores propios extraídos.
• Agrupación Espectralque es una técnica basada en el eigenspectrum de la matriz de similitud de un conjunto de datos para reducir la dimensionalidad de los datos como paso previo a la ejecución de algoritmos de agrupación, como la agrupación de k-means.
• Teoría de Grafos y el análisis de grafos, donde los valores y vectores propios se utilizan para dividir un grafo en comunidades (componentes principales), incrustar el grafo en un espacio de menor dimensión para su visualización, y la sparsificación espectral para aproximar un grafo con un eigenespectro similar.
• Series temporalesdonde se utiliza el análisis de espectro singular para descubrir patrones subyacentes en las series, como tendencias, ciclos y anomalías.

Propiedades del polinomio característico

Como objeto matemático, un polinomio característico tiene algunas propiedades interesantes, entre ellas:

• Monic: El coeficiente principal de un polinomio característico es siempre uno (mónico).
• Titulación: El grado n de un polinomio característico es siempre igual al tamaño de lamatriz nx n asociada.
• Invarianza bajo similitud matricial: Si transformamos una matriz y el resultado es una matriz semejante, ambas tienen un polinomio característico idéntico (es decir, la matriz semejante transformada conserva el polinomio característico original).
• Coeficientes: El primer término principal del polinomio característico es el determinante de la matriz asociada, y el penúltimo coeficiente es la traza sin signo de la matriz asociada c₀=det(A) y c_n-1=-1^n-1tr(A)
• En el polinomio característico, si sustituimos cada incógnita por la matriz cuadrada original, el resultado será una matriz cero (Teorema de Cayley-Hamilton). En otras palabras, el polinomio característico es un polinomio aniquilador de la matriz cuadrada. En esta forma, los valores propios pueden deducirse directamente de la matriz cuadrada. En consecuencia, puede afirmarse que toda matriz cuadrada satisface su propia ecuación característica.

Temas avanzados

Por último, quiero ofrecer algunos detalles más avanzados relacionados con los polinomios característicos y las propiedades de las matrices, como un vistazo más a las matemáticas, pero sin entrar en muchos detalles.

• Polinomio mínimo: Un polinomio mónico estrechamente relacionado con el polinomio característico es el polinomio mínimo, que es un polinomio de grado mínimo positivo que aniquila la matriz cuadrada A. Como un polinomio característico también puede aniquilar su matriz cuadrada, el polinomio mínimo puede derivarse de dicho polinomio característico.
• Similitud y diagonalización: Dos matrices son similares si están relacionadas entre sí mediante una transformación lineal común. Si dos matrices son similares, entonces también tienen el mismo rango, traza, determinante, valores propios, polinomio característico y polinomios mínimos. 
• Ecuación característica de potencias y funciones matriciales: En una matriz potencia, los valores propios se elevan a la k-ésima potencia de la matriz^Ak y el polinomio característico correspondiente se obtiene como det(A^k-λI). Para una función matricial f(x), el polinomio característico puede deducirse evaluando f() en los valores propios de A.

Conclusión

En este artículo hemos aprendido sobre el polinomio característico y las formas en que contiene propiedades importantes de una matriz cuadrada, como los valores propios, la traza y el determinante. Dado el importante papel de los valores propios en la ciencia de datos y el aprendizaje automático, la comprensión de la ecuación característica nos ayuda enormemente a entender cómo el aprendizaje automático y los algoritmos estadísticos extraen los componentes principales de una matriz de datos para encontrar patrones y mejorar la eficiencia computacional.

Si te interesa leer sobre otras ecuaciones importantes y conocidas en la ciencia de datos y el aprendizaje automático, consulta nuestro Tutorial sobre la ecuación normal para la regresión lineal. DataCamp también tiene grandes cursos para un camino de aprendizaje completo y estructurado, como nuestro curso de Álgebra Lineal para la Ciencia de Datos en R, que he mencionado antes y que definitivamente recomiendo.