Diagonalización de matrices: Una guía completa

La diagonalización de matrices es una técnica útil en álgebra lineal que transforma matrices complejas en su forma más simple, que es una matriz diagonal. La diagonalización es útil en múltiples aplicaciones de la ciencia de datos, desde el análisis de componentes principales hasta la resolución de ecuaciones diferenciales y el análisis de cadenas de Markov. 

Este artículo comenzará con los fundamentos de una matriz diagonal, explorará qué hace que una matriz sea diagonalizable y recorrerá paso a paso el proceso de diagonalización con ejemplos detallados. También aprenderemos sobre el sofisticado algoritmo numérico que maneja matrices grandes de manera eficiente.

¿Qué es una matriz diagonal?

Una matriz diagonal es una matriz cuadrada en la que todos los elementos fuera de la diagonal principal son cero. 

En notación matemática, una matriz D es diagonal si D[i,j] = 0 siempre que i ≠ j.

El ejemplo más sencillo es una matriz diagonal de 3×3:

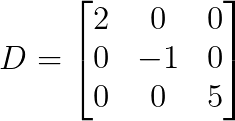
Observa cómo todos los elementos, excepto los diagonales, son cero. ¿Qué hace que estas matrices sean especiales?

¿Por qué son importantes las matrices diagonales?

Las matrices diagonales tienen múltiples ventajas computacionales debido a su estructura simple:

• Simplicidad de la multiplicación: Al multiplicar matrices diagonales, podemos multiplicar los elementos diagonales correspondientes. Por lo tanto, la multiplicación de matrices y vectores solo requiere n multiplicaciones en lugar de n² para matrices generales.
• Cálculo de potencia: Para calcular D^n, podemos elevar cada elemento diagonal a la potencia n, sin necesidad de realizar ninguna multiplicación matricial compleja.
• Cálculo inverso: Si todos los elementos diagonales son distintos de cero, la inversa se puede calcular tomando los recíprocos de los elementos diagonales, evitando así la costosa inversión de la matriz.
• e determinante: El determinante es igual al producto de todos los elementos diagonales.
• Requisitos de almacenamiento: El almacenamiento se reduce de^n² a n elementos, lo que reduce el uso de memoria para matrices grandes.
• Valores propios: Los valores propios son directamente visibles como entradas diagonales, lo que facilita el análisis espectral.
• Resolución de sistemas lineales: Resolver Dx = b se reduce a una división por elementos, lo que convierte una operación compleja en una sencilla.

Estas ventajas computacionales también explican por qué el proceso de diagonalización es una técnica tan valiosa en la computación numérica.

¿Qué es la diagonalización de matrices?

La diagonalización de matrices es el proceso de encontrar una matriz diagonal D y una matriz invertible P tales que:

De manera equivalente, podemos escribir:

Esto demuestra que D es similar a A mediante un cambio de base representado por P.

Geométricamente, la diagonalización revela que muchas transformaciones lineales pueden descomponerse en tres pasos:

1. Cambia a un sistema de coordenadas especial (multiplicación por ^P-1).
2. Aplica una escala simple a lo largo de los ejes de coordenadas (multiplicación por D).
3. Vuelve a las coordenadas originales (multiplicando por P).

Las columnas de P son vectores propios de A, mientras que las entradas diagonales de D son los valores propios correspondientes. Esta conexión entre la diagonalización y el sistema de valores propios puede entenderse como: una matriz es diagonalizable si y solo si tiene suficientes vectores propios linealmente independientes para formar una base.

¿Cuándo se puede diagonalizar una matriz?

Dado que no todas las matrices pueden diagonalizarse, comprendamos el teorema de diagonalización y las condiciones para la diagonalizabilidad antes de aplicar la técnica.

El teorema de la diagonalización

El teorema establece lo siguiente: Una matriz n×n A es diagonalizable si y solo si A tiene n vectores propios linealmente independientes.

Significa que la diagonalizabilidad depende completamente de la estructura geométrica de la transformación, específicamente, de si existe una base compuesta completamente por vectores propios.

Condiciones necesarias y suficientes

Las condiciones para el proceso de diagonalización son las siguientes:

1. Conjunto completo de vectores propios: La matriz tiene n vectores propios linealmente independientes.
2. La multiplicidad geométrica es igual a la multiplicidad algebraica: Para cada valor propio λ, la dimensión de su espacio propio es igual al número de veces que λ aparece como raíz del polinomio característico.
3. El polinomio mínimo tiene factores lineales distintos: El polinomio mínimo se divide completamente en factores lineales distintos.

La prueba más práctica consiste en comprobar si cada valor propio tiene «suficientes» vectores propios. Si un valor propio λ aparece k veces como raíz del polinomio característico, necesitamos exactamente k vectores propios linealmente independientes asociados a λ.

Matrices diagonalizables frente a matrices no diagonalizables

Ciertos tipos de matrices siempre son diagonalizables:

• Matrices simétricas (autovalores reales, autovectores ortogonales)
• Matrices con n valores propios distintos (automáticamente tienen n vectores propios independientes)
• Matrices hermitianas (análogo complejo de las matrices simétricas)

Las matrices no diagonalizables comunes son:

• Matrices nilpotentes (como las matrices triangulares superiores con ceros en la diagonal)
• Bloques de Jordan (matrices con valores propios repetidos pero vectores propios insuficientes)
• Matrices defectuosas (aquellas que carecen de un conjunto completo de vectores propios)

Conceptos erróneos comunes

Antes de continuar, abordemos algunos conceptos erróneos comunes sobre la diagonalizabilidad:

• Diagonalizabilidad ≠ invertibilidad: Se trata de propiedades completamente independientes. Una matriz puede ser diagonalizable pero singular (tener cero como valor propio). Si zero es un valor propio, la matriz no es invertible, pero aún así puede ser diagonalizable. Del mismo modo, una matriz puede ser invertible pero no diagonalizable: Una matriz sin valores propios nulos (por lo tanto invertible) podría carecer aún de suficientes vectores propios. 
• Diagonalizabilidad ≠ tener valores propios reales: Las matrices con valores propios complejos pueden seguir siendo diagonalizables sobre los números complejos.
• Los valores propios repetidos ≠ no diagonalizables: Las matrices pueden tener valores propios repetidos y seguir siendo diagonalizables si tienen suficientes vectores propios.

Hasta ahora, hemos aprendido todos los conceptos relacionados con la diagonalización. Estás más que listo para sumergirte en el proceso paso a paso de la diagonalización, junto con múltiples ejemplos.

Proceso paso a paso para la diagonalización

Veamos paso a paso el proceso de diagonalización de una matriz.

Paso 1: Encontrar valores propios

Primero, resolvemos la ecuación característica para hallar todos los valores propios:

Considerando una matriz 2×2:

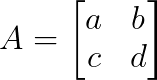
El polinomio característico es:

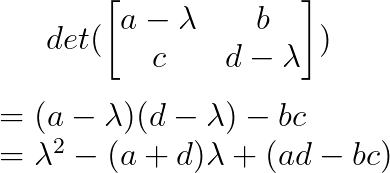
Si igualamos esto a cero y resolvemos, obtenemos los valores propios. Para matrices más grandes, el proceso implica calcular determinantes de matrices (n×n), lo que se vuelve cada vez más complejo.

Paso 2: Encontrar vectores propios

Para cada valor propio λᵢ, resolvemos el sistema para encontrar los vectores propios correspondientes:

Esto implica:

1. Sustituyendo λᵢ en (A — λᵢI)
2. Reduce las filas de la matriz resultante para encontrar el espacio nulo.
3. Expresando la solución general en términos de parámetros libres
4. Selección de vectores propios específicos (normalmente con componentes enteros simples)

El número de vectores propios linealmente independientes para cada valor propio determina si la diagonalización es posible.

Paso 3: Construcción de P y D

Una vez que tenemos todos los vectores propios:

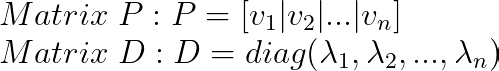
Aquí, el orden del valor es importante; la columna i-ésima de P debe corresponder a la entrada diagonal i-ésima de D.

Finalmente, podemos verificar la diagonalización mediante:

1. Calcular ^{P-1 (} o comprobar que P es invertible)
2. Verificar que A = ^PDP-1 o, de forma equivalente, D = ^P-1AP.
3. Comprobando que Avᵢ = λᵢvᵢ para cada par de vectores propios y valores propios.

El orden de los vectores propios en P es arbitrario, pero una vez elegido, determina el orden de los valores propios en D. Diferentes ordenaciones dan lugar a diagonalizaciones diferentes pero equivalentes.

Ejemplos resueltos de diagonalización

Analicemos diferentes escenarios para consolidar nuestra comprensión del proceso de diagonalización.

Ejemplo 1: Matriz con valores propios distintos

Considera la matriz:

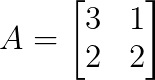
Trabajamos en el primer paso para hallar los valores propios escribiendo el polinomio característico como:

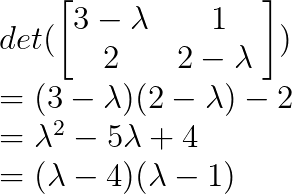
Por lo tanto, λ₁ = 4 y λ₂ = 1.

A continuación, podemos hallar los vectores propios sustituyendo los valores de λ.

Para λ₁ = 4:

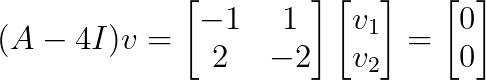
Esto da v₁ = [1, 1]ᵀ

Sustituyendo λ₂ = 1:

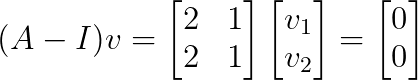
Esto da v₂ = [1, -2]ᵀ

Podemos construir la diagonalización como:

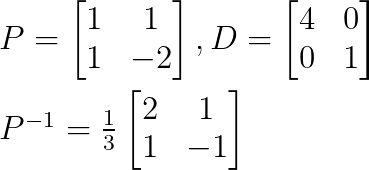
Dado que hemos encontrado todas las matrices P, D y ^P-1, podemos diagonalizar la matriz original.

Ejemplo 2: Matriz con valores propios repetidos

Considera lo siguiente:

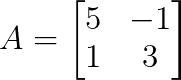
Hallamos los valores propios mediante el polinomio característico:

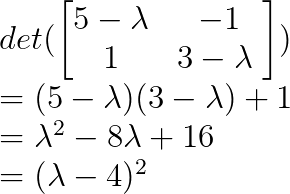
Por lo tanto, λ = 4 es un valor propio repetido con multiplicidad algebraica 2.

Encontremos los vectores propios para λ = 4:

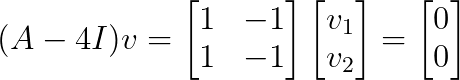
Este sistema tiene rango 1, lo que nos da un espacio propio unidimensional con vector base v = [1, 1]ᵀ.

Dado que solo tenemos un vector propio linealmente independiente para un valor propio de multiplicidad 2, esta matriz no es diagonalizable. no diagonalizable.

Ejemplo 3: Valores propios complejos

Considera la matriz de rotación:

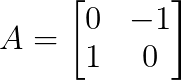
Podemos hallar los valores propios mediante el polinomio característico:

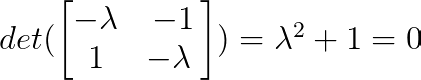
Por lo tanto, λ₁ = i y λ₂ = -i (donde i es la unidad imaginaria).

A continuación, hallamos los vectores propios. Para λ₁ = i:

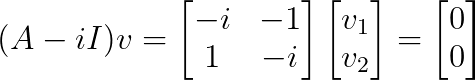
Esto da v₁ = [1, -i]ᵀ

For λ₂ = -i:

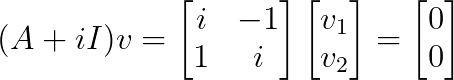
Esto da v₂ = [1, i]ᵀ

Este es un ejemplo clásico de diagonalización compleja:

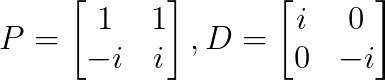
Esta matriz es diagonalizable sobre los números complejos, pero no sobre los números reales.

Métodos computacionales y consideraciones numéricas

Aunque los cálculos manuales funcionan bien para matrices pequeñas, las aplicaciones prácticas requieren algoritmos numéricos que puedan manejar matrices grandes de manera eficiente.

El algoritmo QR

El algoritmo QR es el método estándar para hallar valores propios en el software moderno. En lugar de resolver polinomios característicos (lo cual resulta poco práctico para matrices grandes), utiliza un enfoque iterativo que revela gradualmente los valores propios.

El algoritmo funciona mediante transformaciones repetidas:

1. Descomponer: Aₖ = QₖRₖ (descomposición QR)
2. Formulario: Aₖ₊₁ = RₖQₖ
3. Repite hasta que converja.

Con cada iteración, la matriz se vuelve más triangular, conservando sus valores propios. Finalmente, los valores propios aparecen a lo largo de la diagonal. Para matrices simétricas, el resultado es una matriz diagonal, lo que nos da directamente la diagonalización.

Las implementaciones modernas mejoran este algoritmo básico con:

• Preprocesamiento para reducir el coste computacional
• Cambios que aceleran la convergencia
• Métodos para extraer valores propios convergentes de forma temprana
• Técnicas especiales para pares de valores propios complejos

Acondicionamiento y estabilidad numérica

No todos los problemas de diagonalización son igualmente estables. El factor clave es cuán «separados» están los vectores propios. Cuando los vectores propios apuntan casi en la misma dirección, pequeños errores numéricos pueden provocar grandes errores en los resultados.

Esta inestabilidad se manifiesta de varias maneras:

• Autovalores cercanos: Cuando los valores propios son muy similares, sus vectores propios se vuelven difíciles de distinguir numéricamente.
• Matrices casi defectuosas: Las matrices que son casi no diagonalizables tienen vectores propios extremadamente sensibles.
• Errores de redondeo: La aritmética informática puede amplificar pequeños errores y convertirlos en imprecisiones significativas.

Cuando se enfrentan a estos casos inestables, las bibliotecas numéricas suelen utilizar descomposiciones alternativas que sacrifican la simplicidad de la forma diagonal para mejorar el comportamiento numérico.

Trabajar con matrices grandes

Se aplican diferentes estrategias en función del tamaño y la estructura de nuestra matriz.

Para matrices dispersas (en su mayoría ceros), algoritmos especializados como los métodos Lanczos o Arnoldi encuentran valores propios sin necesidad de formar la matriz completa. Esto funciona bien cuando la matriz es demasiado grande para almacenarla.

Cuando solo necesitamos unos pocos valores propios (como el mayor o el menor), los métodos iterativos pueden encontrarlos directamente sin calcular todo el espectro.

Para problemas de gran envergadura, los algoritmos paralelos dividen el trabajo entre varios procesadores, mientras que los métodos sin matrices evitan almacenar la matriz por completo, ya que solo necesitan la capacidad de multiplicarla por vectores.

El mejor enfoque depende generalmente de las necesidades específicas del problema que se está resolviendo: la estructura de la matriz, el número de valores propios necesarios y la precisión requerida para nuestra aplicación.

Conclusión

La diagonalización de matrices transforma transformaciones lineales complejas en su forma más simple, revelando su estructura a través de los valores propios y los vectores propios. Hemos explorado cuándo se pueden diagonalizar las matrices, lo que requiere un conjunto completo de vectores propios linealmente independientes, y hemos recorrido el proceso sistemático para encontrar estas descomposiciones propias.

A través de ejemplos prácticos, hemos visto cómo los valores propios distintos garantizan la diagonalizabilidad, mientras que los valores propios repetidos requieren un análisis de los espacios propios. También hemos examinado casos en los que la diagonalización falla y hemos aprendido los métodos numéricos que hacen que la diagonalización a gran escala sea computacionalmente viable.

Para profundizar en las diagonalizaciones de matrices y sus aplicaciones en la ciencia de datos, te recomendamos que te inscribas en nuestro curso Álgebra lineal para la ciencia de datos, donde dominarás estos conceptos a través de implementaciones prácticas y ejemplos del mundo real.