Matriz singular: Conceptos clave y ejemplos en Ciencia de Datos

Una matriz singular es una matriz cuadrada que no puede invertirse, es decir, que no tiene inversa multiplicativa. Este concepto fundamental del álgebra lineal tiene una inmensa repercusión en las aplicaciones de la ciencia de datos, desde los algoritmos de machine learning hasta la estabilidad numérica en los métodos computacionales.

En este artículo, definiremos qué hace que una matriz sea singular y exploraremos sus propiedades y características matemáticas. Luego examinaremos métodos para detectar matrices singulares. Comprenderemos sus implicaciones reales en la ciencia de datos, y aprenderemos a manejarlas con eficacia.

¿Qué es una matriz singular?

Una matriz singular es una matriz cuadrada cuyo determinante es igual a cero, lo que la hace no invertible. 

En términos matemáticos, para una matriz cuadrada A, si det(A) = 0, entonces A es singular y no tiene matriz inversa A-¹.

La característica fundamental de una matriz singular es que sus filas o columnas son linealmente dependientes, lo que significa que al menos una fila (o columna) puede expresarse como una combinación lineal de las demás filas (o columnas). Esta dependencia crea una "deficiencia" en la matriz que impide que tenga una inversa única.

Otra forma de entender las matrices singulares es a través de su rango. Una matriz cuadrada es singular si y sólo si su rango es menor que su número de filas (o columnas). El rango representa el número máximo de filas o columnas linealmente independientes, por lo que cuando éste es inferior a las dimensiones de la matriz, se produce la singularidad.

Este concepto es importante porque muchos algoritmos se basan en la inversión de matrices, desde la resolución de problemas de regresión lineal hasta la aplicación de determinadas técnicas de machine learning. Cuando una matriz es singular, estas operaciones fallan, requiriendo enfoques alternativos o pasos de preprocesamiento para manejar la situación.

Propiedades y condiciones de las matrices singulares

Comprender las propiedades matemáticas de las matrices singulares ayuda a identificar posibles problemas antes de que causen problemas computacionales en los flujos de trabajo de la ciencia de datos.

• Determinante cero: El determinante de una matriz singular siempre es igual a cero, lo que indica directamente la no invertibilidad. Este determinante cero significa que la transformación de la matriz no es biyectiva, lo que permite asignar múltiples vectores de entrada a la misma salida.
• Dependencia lineal: Las matrices singulares contienen filas o columnas linealmente dependientes, en las que al menos una fila puede expresarse como combinación lineal de las demás. Esta dependencia crea información redundante que provoca problemas de cálculo.
• Deficiencia de rango: Una matriz singular n×n tiene rango menor que n, posee menos filas o columnas linealmente independientes que su dimensión. Esta deficiencia explica por qué los sistemas en los que intervienen matrices singulares carecen de soluciones únicas.
• Valores propios cero: Al menos un valor propio de una matriz singular es exactamente cero, lo que corresponde a direcciones en el espacio que se colapsan completamente durante la transformación. El número de valores propios cero es igual a la nulidad de la matriz.
• Espacio nulo no trivial: Las matrices singulares tienen vectores distintos de cero que, al multiplicarse por la matriz, producen el vector cero. La dimensión de este espacio nulo indica cuánta información se pierde durante la transformación.

Ahora que hemos comprendido las propiedades fundamentales de una matriz singular, vamos a contrastarlas con las matrices no singulares.

Singular vs. Matriz no singular

Las matrices no singulares son invertibles y admiten cálculos numéricos fiables, mientras que las matrices singulares carecen de inversas y requieren un manejo especializado. Esta división fundamental determina la viabilidad computacional en todas las aplicaciones de la ciencia de datos. 

Estas diferencias se aplican a cada una de las propiedades fundamentales de una matriz singular que vimos anteriormente. La tabla siguiente resume las diferencias entre matrices singulares y no singulares:

Ejemplos de matrices singulares

Examinar ejemplos concretos ayuda a ilustrar cómo se manifiesta la singularidad en la práctica y crea intuición para reconocer estas matrices.

Matriz singular simple 2×2

Considera este ejemplo básico en el que una fila es múltiplo de otra:

Matriz singular simple 2×2 (Imagen del autor)

Aquí, la segunda fila es exactamente la mitad de la primera, lo que crea una dependencia lineal. El determinante es (2×2) - (4×1) = 0, lo que confirma la singularidad.

Fila o columna cero

Cualquier matriz que contenga una fila o columna de todos ceros es automáticamente singular:

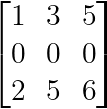
Fila o columna cero (Imagen del autor)

La fila cero hace imposible que la matriz tenga rango completo, independientemente de las demás entradas.

Filas o columnas idénticas

Las matrices con filas o columnas idénticas son siempre singulares:

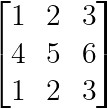
Filas o columnas idénticas (Imagen del Autor)

La primera y la tercera fila son idénticas, creando una dependencia lineal perfecta.

Dependencia de la combinación lineal

Una singularidad más sutil se produce cuando una fila es igual a una combinación de otras:

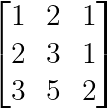
Dependencia de la combinación lineal (Imagen del autor)

Aquí, la tercera fila es igual a la suma de las dos primeras filas: [3,5,2] = [1,2,1] + [2,3,1].

Cada uno de estos ejemplos anteriores demuestra cómo matrices aparentemente diferentes pueden compartir la propiedad fundamental de dependencia lineal que define la singularidad.

¿Por qué aparecen matrices singulares en la Ciencia de Datos?

Las matrices singulares aparecen con frecuencia en las aplicaciones de la ciencia de datos debido a la naturaleza de los datos del mundo real y a los flujos de trabajo analíticos habituales.

Multicolinealidad en conjuntos de características

La fuente más común de matrices singulares en la ciencia de datos es la multicolinealidad, cuando varias características de un conjunto de datos están perfectamente o casi perfectamente correlacionadas. Esto crea una dependencia lineal entre las columnas de la matriz de diseño, lo que provoca una singularidad durante las operaciones matriciales.

Considera un conjunto de datos de venta al por menor en el que tienes características para total_sales, q1_sales, q2_sales, q3_sales, y q4_sales. Si los valores de las ventas trimestrales siempre suman exactamente las ventas totales, entonces:

total_sales = q1_sales + q2_sales + q3_sales + q4_sales

Cuando esta relación se mantiene perfectamente en todas las observaciones, la matriz de diseño resultante se vuelve singular. Cualquier algoritmo de regresión lineal que intente invertir esta matriz fracasará porque una columna puede predecirse perfectamente a partir de las demás.

Ocurren situaciones similares con características derivadas como

• Temperatura en grados Celsius y Fahrenheit
• Edad y año de nacimiento (dado un año de referencia fijo)
• Ratios en los que el numerador y el denominador también son características
• Variables ficticias que suman una constante (la trampa de las variables ficticias)

Datos insuficientes relativos a las características

Los conjuntos de datos de alta dimensión con menos observaciones que características producen naturalmente matrices singulares. Cuando tienes n muestras pero p características donde p > n, la matriz de covarianza o matriz grama resultante de n×n tendrá rango como máximo n, lo que la hace singular si necesitas una matriz p×p invertible.

Esta "maldición de la dimensionalidad" afecta comúnmente:

• Datos genómicos con miles de genes pero cientos de muestras
• Análisis de textos con grandes vocabularios pero documentos limitados
• Procesamiento de imágenes con características de alta resolución pero conjuntos de entrenamiento pequeños
• Modelización financiera con muchos indicadores económicos, pero series temporales cortas

Preprocesamiento de datos 

Los pasos habituales del preprocesamiento de datos pueden introducir inadvertidamente la singularidad:

• Centrar las transformaciones: Centrar cada rasgo (restando la media) no causa singularidad por sí solo, pero en presencia de otras dependencias lineales, puede preservarlas o acentuarlas. En los casos en que los rasgos ya son casi dependientes, el centrado puede acercarlos a la dependencia exacta con una precisión limitada.
• Escalado y normalización: Ciertas operaciones de escalado pueden hacer que las relaciones lineales sutiles sean más pronunciadas, empujando los rasgos casi dependientes a la dependencia perfecta, debido a los límites de precisión del punto flotante.
• Ingeniería de funciones: Crear características polinómicas, términos de interacción o expansiones de base puede introducir relaciones lineales inesperadas. Por ejemplo, si creas las características x, ^x² y ^2x²- x, la tercera característica(^2x²- x) está perfectamente determinada por las dos primeras.

Comprender estas fuentes comunes de singularidad permite a los científicos de datos aplicar medidas preventivas en una fase temprana de sus flujos de trabajo, como la comprobación de la multicolinealidad durante el análisis exploratorio de datos o el uso proactivo de técnicas de regularización.

Ahora que entendemos por qué se producen matrices singulares en la ciencia de datos, exploremos métodos prácticos para detectarlas antes de que provoquen fallos computacionales.

Cómo detectar matrices singulares

La forma más directa de detectar una matriz singular es comprobando su determinante. Si el determinante de una matriz cuadrada es cero, la matriz es singular y no invertible. Este método es sencillo, matemáticamente sólido y muy utilizado en la práctica.

Veamos cómo realizar esta comprobación utilizando Python:

import numpy as np

# Example 2x2 matrix
A = np.array([[2, 4],
             [1, 2]])

# Calculate the determinant
det_A = np.linalg.det(A)

print(f"Determinant of A: {det_A}")

# Check if matrix is singular
if np.isclose(det_A, 0):
   print("Matrix A is singular.")
else:
   print("Matrix A is non-singular.")

En el ejemplo anterior, definimos una matriz Ade 2×2 y utilizamos np.linalg.det() para calcular su determinante. Como la aritmética de coma flotante puede introducir pequeños errores numéricos, utilizamos np.isclose() para comprobar si el determinante es efectivamente cero. Si lo es, concluimos que la matriz es singular. 

Veremos a continuación el resultado que confirma la singularidad:

Salida que detecta la matriz singular. (Imagen del autor)

Este método es a la vez intuitivo y práctico, lo que lo convierte en un primer paso fiable a la hora de diagnosticar problemas relacionados con la invertibilidad de matrices en los flujos de trabajo de la ciencia de datos.

Cómo manejar matrices singulares en la práctica

Cuando se encuentran matrices singulares en los flujos de trabajo de la ciencia de datos, varias estrategias pueden resolver los retos computacionales preservando la integridad analítica.

Técnicas de regularización

Añadir pequeños valores a la diagonal (regularización de Ridge) es el método más habitual para tratar matrices casi sinulares en problemas de regresión. Esta técnica transforma las matrices singulares en invertibles manteniendo la estabilidad numérica:

# Ridge regularization approach
lambda_reg = 1e-6
A_regularized = A + lambda_reg * np.eye(A.shape[0])

Cálculo pseudoinverso

La pseudoinversa de Moore-Penrose proporciona una inversa generalizada para matrices singulares, ofreciendo la "mejor" solución en un sentido de mínimos cuadrados:

# Using pseudoinverse for singular matrices
A_pinv = np.linalg.pinv(A)
x = A_pinv @ b 

Reducción de la dimensionalidad

Eliminar los rasgos linealmente dependientes elimina la singularidad ensu origen. El análisis de componentes principales o lastécnicas de selección de características pueden identificar y eliminar las dimensiones redundantes:

# PCA-based dimensionality reduction
from sklearn.decomposition import PCA
pca = PCA(n_components=0.95) 
X_reduced = pca.fit_transform(X)

Algoritmos alternativos

Algunos algoritmos están diseñados específicamente para tratar matrices singulares. La descomposición QR con pivotaje puede resolver sistemas lineales incluso cuando la matriz de coeficientes es singular, proporcionando soluciones cuando existen e identificando incoherencias cuando no existen.

Estas estrategias garantizan que las matrices singulares no descarrilen los proyectos de ciencia de datos, al tiempo que mantienen el rigor matemático y la interpretabilidad de los resultados.

Conclusión

Este artículo exploró las matrices singulares, que aprendimos que son matrices cuadradas con determinantes nulos que no pueden invertirse debido a dependencias lineales entre filas o columnas. Examinamos por qué suelen aparecer en la ciencia de datos, desde la multicolinealidad y los datos de alta dimensión hasta los problemas introducidos durante el preprocesamiento. 

En este artículo, también revisamos las formas de detectar y tratar las matrices singulares mediante técnicas básicas como la comprobación de determinantes, la regularización, los pseudoinversos y la reducción de la dimensionalidad. (Si sigues interesado en profundizar por tu cuenta, herramientas como el análisis de números de condición o la descomposición de valores singulares pueden ofrecerte aún más información sobre el comportamiento de las matrices y la estabilidad numérica).

Para profundizar en tu comprensión del álgebra lineal y su papel fundamental en las aplicaciones de la ciencia de datos, inscríbete en nuestro curso de Álgebra Lineal para la Ciencia de Datos, donde dominarás estos conceptos fundamentales y sus implementaciones en escenarios del mundo real.