Matrixdiagonalisierung: Ein umfassender Leitfaden

Die Matrixdiagonalisierung ist eine coole Technik in der linearen Algebra, mit der man komplexe Matrizen in ihre einfachste Form, nämlich eine Diagonalmatrix, umwandeln kann. Diagonalisierung ist in der Datenwissenschaft für viele Sachen nützlich, von der Hauptkomponentenanalyse bis hin zur Lösung von Differentialgleichungen und der Analyse von Markov-Ketten. 

In diesem Artikel geht's um die Grundlagen einer diagonalen Matrix, was eine Matrix diagonalisierbar macht und wie man sie Schritt für Schritt mit detaillierten Beispielen diagonalisiert. Wir werden auch etwas über den raffinierten numerischen Algorithmus lernen, der große Matrizen effizient verarbeitet.

Was ist eine diagonale Matrix?

Eine diagonale Matrix ist eine quadratische Matrix, bei der alle Elemente außerhalb der Hauptdiagonalen Null sind. 

In der Mathe-Sprache ist eine Matrix D diagonal, wenn D[i,j] = 0 ist, wenn i ≠ j.

Das einfachste Beispiel ist eine 3×3-Diagonalmatrix:

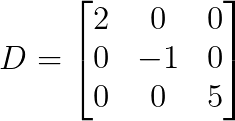
Schau dir an, dass alle Elemente außer den diagonalen null sind. Was macht diese Matrizen so besonders?

Warum sind diagonale Matrizen wichtig?

Diagonale Matrizen haben wegen ihrer einfachen Struktur mehrere Vorteile bei Berechnungen:

• Einfache Multiplikation: Bei der Multiplikation diagonaler Matrizen können wir die entsprechenden diagonalen Elemente miteinander multiplizieren. So braucht man für die Matrix-Vektor-Multiplikation nur n Multiplikationen statt n² für allgemeine Matrizen.
• Leistungsberechnungs: Um D^n zu berechnen, können wir jedes diagonale Element mit n potenzieren, ohne dass wir komplizierte Matrixmultiplikationen machen müssen.
• Umgekehrte Berechnung: Wenn alle Diagonalelemente ungleich Null sind, kann die Umkehrung berechnet werden, indem man die Kehrwerte der Diagonalelemente nimmt, wodurch eine aufwendige Matrixinversion vermieden wird.
• Bestimmende Faktoren: Der Determinante ist das Produkt aller Diagonalelemente.
• Lagerungshinweise: Der Speicherbedarf sinkt von^n² auf n Elemente, was den Speicherverbrauch für große Matrizen reduziert.
• Eigenwerte: Eigenwerte sind direkt als diagonale Einträge zu sehen, was die Spektralanalyse echt einfach macht.
• Lösen linearer Gleichungssysteme: Das Lösen von Dx = b wird zu einer elementweisen Division, wodurch eine komplizierte Operation zu einer einfachen wird.

Diese rechnerischen Vorteile erklären auch, warum die Diagonalisierung so eine wichtige Technik in der numerischen Berechnung ist.

Was ist Matrixdiagonalisierung?

Matrixdiagonalisierung ist der Vorgang, bei dem eine diagonale Matrix D und eine invertierbare Matrix P so gefunden werden, dass:

Gleichwertig können wir schreiben:

Das zeigt, dass D durch eine Änderung der Basis, die durch P dargestellt wird, ähnlich wie A ist.

Geometrisch gesehen zeigt die Diagonalisierung, dass viele lineare Transformationen in drei Schritte zerlegt werden können:

1. Wechsel zu einem speziellen Koordinatensystem (Multiplikation mit ^P-1)
2. Mach einfach eine Skalierung entlang der Koordinatenachsen (mal mit D).
3. Zurück zu den ursprünglichen Koordinaten (mal P)

Die Spalten von P sind Eigenvektoren von A, während die Diagonalelemente von D die entsprechenden Eigenwerte sind. Diese Verbindung zwischen Diagonalisierung und dem Eigensystem kann man so verstehen: Eine Matrix ist genau dann diagonalisierbar, wenn sie genug linear unabhängige Eigenvektoren hat, um eine Basis zu bilden.

Wann kann eine Matrix diagonalisiert werden?

Da nicht alle Matrizen diagonalisiert werden können, schauen wir uns erst mal den Diagonalisierungssatz und die Bedingungen für die Diagonalisierbarkeit an, bevor wir die Technik anwenden.

Der Diagonalisierungssatz

Der Satz besagt: Eine n×n-Matrix A ist genau dann diagonaliserbar, wenn sie n linear unabhängige Eigenvektoren hat.

Das heißt, dass die Diagonalisierbarkeit komplett von der geometrischen Struktur der Transformation abhängt, genauer gesagt davon, ob es eine Basis gibt, die nur aus Eigenvektoren besteht.

Notwendige und ausreichende Bedingungen

Die Bedingungen für den Diagonalisierungsprozess sind wie folgt:

1. Vollständiger Satz von Eigenvektoren: Die Matrix hat n linear unabhängige Eigenvektoren.
2. Die geometrische Multiplizität ist gleich der algebraischen Multiplizität: Für jeden Eigenwert λ ist die Dimension seines Eigenraums gleich der Anzahl, wie oft λ als Wurzel des charakteristischen Polynoms auftaucht.
3. Das Minimalpolynom hat verschiedene lineare Faktoren: Das Minimalpolynom lässt sich komplett in verschiedene lineare Faktoren aufteilen.

Der praktischste Test ist, zu checken, ob jeder Eigenwert „genug“ Eigenvektoren hat. Wenn ein Eigenwert λ k-mal als Wurzel des charakteristischen Polynoms auftaucht, brauchen wir genau k linear unabhängige Eigenvektoren, die mit λ verbunden sind.

Diagonalisierbare vs. nicht diagonalisierbare Matrizen

Bestimmte Matrixarten sind immer diagonaliserbar:

• Symmetrische Matrizen (reelle Eigenwerte, orthogonale Eigenvektoren)
• Matrizen mit n verschiedenen Eigenwerten (die automatisch n unabhängige Eigenvektoren haben)
• Hermitische Matrizen (komplexes Analogon zu symmetrischen Matrizen)

Häufige nicht diagonalisierbare Matrizen sind:

• Nilpotente Matrizen (wie obere Dreiecksmatrizen mit Nullen auf der Diagonalen)
• Jordan-Blöcke (Matrizen mit wiederholten Eigenwerten, aber nicht genug Eigenvektoren)
• Defekte Matrizen (die keinen kompletten Satz von Eigenvektoren haben)

Häufige Missverständnisse

Bevor wir weitermachen, lass uns ein paar häufige Missverständnisse zum Thema Diagonalisierbarkeit klären:

• Diagonalisierbarkeit ≠ Invertierbarkeit: Das sind komplett verschiedene Sachen. Eine Matrix kann diagonalisierbar, aber singulär sein (mit Null als Eigenwert). Wenn zero ein Eigenwert ist, ist die Matrix nicht invertierbar, kann aber trotzdem diagonalisierbar sein. Genauso kann eine Matrix invertierbar, aber nicht diagonalisierbar sein: Eine Matrix ohne Eigenwerte Null (also invertierbar) kann trotzdem nicht genügend Eigenvektoren haben. 
• Diagonalisierbarkeit ≠ reelle Eigenwerte: Matrizen mit komplexen Eigenwerten können trotzdem über den komplexen Zahlen diagonalisierbar sein.
• Wiederholte Eigenwerte ≠ nicht diagonalisierbare: Matrizen können wiederholte Eigenwerte haben und trotzdem diagonaliserbar sein, wenn sie genügend Eigenvektoren haben.

Bis jetzt haben wir alle Konzepte rund um die Diagonalisierung gelernt. Du bist jetzt voll bereit, dich Schritt für Schritt in die Diagonalisierung zu stürzen, und das mit vielen Beispielen.

Schritt für Schritt zur Diagonalisierung

Lass uns Schritt für Schritt durch den Prozess der Diagonalisierung einer Matrix gehen.

Schritt 1: Eigenwerte finden

Zuerst lösen wir die charakteristische Gleichung, um alle Eigenwerte zu finden:

Betrachten wir mal eine 2×2-Matrix:

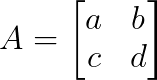
Das charakteristische Polynom ist:

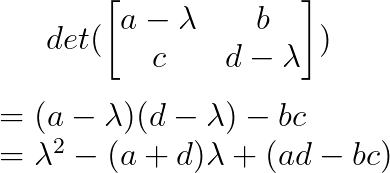
Wenn wir das hier auf Null setzen und das Ganze lösen, kriegen wir die Eigenwerte. Bei größeren Matrizen muss man die Determinanten von (n×n)-Matrizen berechnen, was immer komplizierter wird.

Schritt 2: Eigenvektoren finden

Für jeden Eigenwert λᵢ lösen wir das System, um die passenden Eigenvektoren zu finden:

Dazu gehört:

1. Ersetze λᵢ in (A — λᵢI)
2. Reduzierung der Zeilen der resultierenden Matrix, um den Nullraum zu finden
3. Die allgemeine Lösung in Form von freien Parametern ausdrücken
4. Auswahl bestimmter Eigenvektoren (normalerweise mit einfachen ganzzahligen Komponenten)

Die Anzahl der linear unabhängigen Eigenvektoren für jeden Eigenwert entscheidet, ob eine Diagonalisierung möglich ist.

Schritt 3: P und D erstellen

Sobald wir alle Eigenvektoren haben:

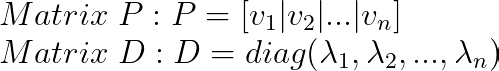
Hier kommt es auf die Reihenfolge der Werte an: Die i-te Spalte von P muss mit dem i-ten Diagonalelement von D übereinstimmen.

Zum Schluss können wir die Diagonalisierung überprüfen, indem wir:

1. Berechne ^{P-1 (} oder schau, ob P umkehrbar ist)
2. Überprüfen, ob A = ^PDP-1 oder D = ^P-1AP
3. Überprüfen, ob Avᵢ = λᵢvᵢ für jedes Eigenvektor-Eigenwert-Paar gilt

Die Reihenfolge der Eigenvektoren in P ist beliebig, aber wenn sie mal festgelegt ist, bestimmt sie die Reihenfolge der Eigenwerte in D. Unterschiedliche Reihenfolgen führen zu unterschiedlichen, aber gleichwertigen Diagonalisierungen.

Ausgearbeitete Beispiele zur Diagonalisierung

Lass uns verschiedene Szenarien durchgehen, um unser Verständnis des Diagonalisierungsprozesses zu festigen.

Beispiel 1: Matrix mit unterschiedlichen Eigenwerten

Schau dir mal diese Matrix an:

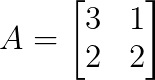
Wir machen den ersten Schritt, um die Eigenwerte zu finden, indem wir das charakteristische Polynom so schreiben:

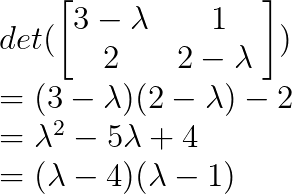
Also ist λ₁ = 4 und λ₂ = 1.

Als Nächstes können wir die Eigenvektoren finden, indem wir Werte für λ einsetzen.

Für λ₁ = 4:

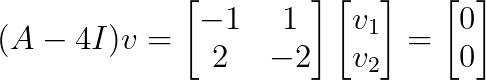
Das ergibt v₁ = [1, 1]ᵀ

Ersetze λ₂ = 1:

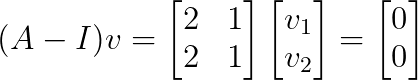
Das ergibt v₂ = [1, -2]ᵀ

Wir können die Diagonalisierung so aufbauen:

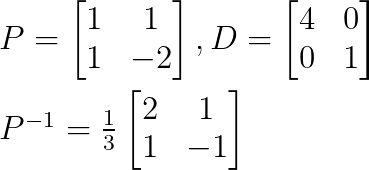
Da wir alle Matrizen P, D und ^P-1 gefunden haben, können wir die ursprüngliche Matrix diagonalisieren.

Beispiel 2: Matrix mit wiederholten Eigenwerten

Bedenk mal:

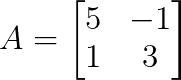
Lass uns die Eigenwerte über das charakteristische Polynom finden:

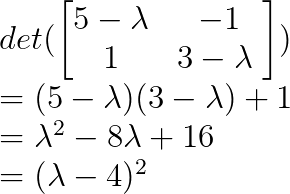
Also ist λ = 4 ein wiederholter Eigenwert mit algebraischer Multiplizität 2.

Lass uns die Eigenvektoren für λ = 4 finden:

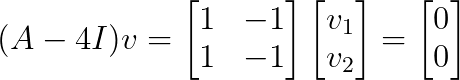
Dieses System hat Rang 1, was uns einen eindimensionalen Eigenraum mit dem Basisvektor v = [1, 1]ᵀ gibt.

Da wir nur einen linear unabhängigen Eigenvektor für einen Eigenwert der Multiplizität 2 haben, ist diese Matrix nicht diagonaliserbar.

Beispiel 3: Komplexe Eigenwerte

Schau dir mal die Rotationsmatrix an:

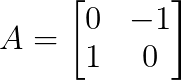
Die Eigenwerte können wir über das charakteristische Polynom finden:

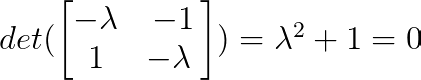
Also ist λ₁ = i und λ₂ = -i (wobei i die imaginäre Einheit ist).

Als Nächstes suchen wir die Eigenvektoren. Für λ₁ = i:

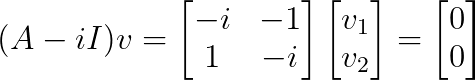
Das ergibt v₁ = [1, -i]ᵀ

Für λ₂ = -i:

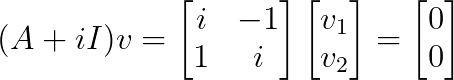
Das ergibt v₂ = [1, i]ᵀ

Das ist ein typisches Beispiel für eine komplizierte Diagonalisierung:

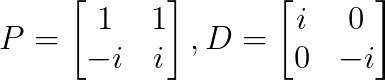
Diese Matrix ist über den komplexen Zahlen diagonalisierbar, aber nicht über den reellen Zahlen.

Rechenmethoden und numerische Überlegungen

Während manuelle Berechnungen für kleine Matrizen gut funktionieren, braucht man in der Praxis numerische Algorithmen, die große Matrizen effizient verarbeiten können.

Der QR-Algorithmus

Der QR-Algorithmus ist die Standardmethode zum Finden von Eigenwerten in moderner Software. Anstatt charakteristische Polynome zu lösen (was bei großen Matrizen ziemlich nervig wird), nutzt es einen iterativen Ansatz, der nach und nach die Eigenwerte aufdeckt.

Der Algorithmus funktioniert durch wiederholte Umwandlungen:

1. Zerlegen: Aₖ = QₖRₖ (QR decomposition)
2. Formular: Aₖ₊₁ = RₖQₖ
3. Wiederhole das, bis alles passt.

Mit jeder Iteration wird die Matrix dreieckiger, während ihre Eigenwerte erhalten bleiben. Schließlich tauchen die Eigenwerte entlang der Diagonalen auf. Bei symmetrischen Matrizen ist das Ergebnis eine Diagonalmatrix, die uns direkt die Diagonalisierung liefert.

Moderne Implementierungen verbessern diesen grundlegenden Algorithmus durch:

• Vorverarbeitung zur Reduzierung des Rechenaufwands
• Veränderungen, die die Konvergenz beschleunigen
• Methoden zur frühzeitigen Extraktion konvergenter Eigenwerte
• Spezielle Techniken für komplizierte Eigenwertpaare

Konditionierung und numerische Stabilität

Nicht alle Diagonalisierungsprobleme sind gleich stabil. Der entscheidende Faktor ist, wie „getrennt“ die Eigenvektoren sind. Wenn Eigenvektoren fast in die gleiche Richtung zeigen, können kleine Rechenfehler zu großen Fehlern in den Ergebnissen führen.

Diese Instabilität zeigt sich auf verschiedene Weise:

• Schließe Eigenwert: Wenn Eigenwerte sehr ähnlich sind, werden ihre Eigenvektoren numerisch schwer zu unterscheiden.
• Fast defekte Matrix: Matrizen, die fast nicht diagonalisierbar sind, haben extrem empfindliche Eigenvektoren.
• Rundungsfehler: Computer-Rechenfehler können kleine Fehler zu echten Problemen machen.

In solchen unstabilen Fällen greifen numerische Bibliotheken oft auf alternative Zerlegungen zurück, die die Einfachheit der Diagonalform zugunsten eines besseren numerischen Verhaltens opfern.

Arbeiten mit großen Matrizen

Je nach Größe und Aufbau unserer Matrix gibt's unterschiedliche Strategien.

Bei spärlichen Matrizen (die meistens nur Nullen haben) gibt es spezielle Algorithmen wie die Lanczos- oder Arnoldi-Methode, die Eigenwerte finden, ohne die ganze Matrix zu berechnen. Das klappt gut, wenn die Matrix zu groß ist, um sie zu speichern.

Wenn wir nur ein paar Eigenwerte brauchen (wie den größten oder kleinsten), können iterative Methoden sie direkt finden, ohne das ganze Spektrum durchzurechnen.

Bei großen Problemen teilen parallele Algorithmen die Arbeit auf mehrere Prozessoren auf, während matrixfreie Methoden die Speicherung der Matrix komplett vermeiden und nur die Fähigkeit benötigen, sie mit Vektoren zu multiplizieren.

Der beste Ansatz hängt meistens davon ab, was genau du lösen willst: die Matrixstruktur, wie viele Eigenwerte du brauchst und wie genau das Ergebnis für deine Anwendung sein muss.

Fazit

Die Matrixdiagonalisierung macht komplizierte lineare Transformationen in ihrer einfachsten Form sichtbar und zeigt ihre Struktur durch Eigenwerte und Eigenvektoren. Wir haben uns angesehen, wann Matrizen diagonalisiert werden können, wofür ein kompletter Satz linear unabhängiger Eigenvektoren nötig ist, und sind den systematischen Prozess zum Finden dieser Eigenzerlegungen durchgegangen.

Anhand von praktischen Beispielen haben wir gesehen, wie unterschiedliche Eigenwerte die Diagonalizierbarkeit garantieren, während sich wiederholende Eigenwerte eine Analyse der Eigenräume erfordern. Wir haben auch Fälle untersucht, in denen die Diagonalisierung nicht klappt, und haben numerische Methoden kennengelernt, die die Diagonalisierung in großem Maßstab rechnerisch machbar machen.

Wenn du dich mehr mit Matrixdiagonalisierungen und ihren Anwendungen in der Datenwissenschaft beschäftigen willst, solltest du unseren Kurs „Lineare Algebra für Datenwissenschaft“ checken. Dort lernst du diese Konzepte anhand praktischer Übungen und Beispiele aus der Praxis.