Diagonalisation d'une matrice : Un guide complet

La diagonalisation d'une matrice est une technique utile en algèbre linéaire qui transforme des matrices complexes en leur forme la plus simple, à savoir une matrice diagonale. La diagonalisation est utile dans de nombreuses applications de la science des données, allant de l'analyse en composantes principales à la résolution d'équations différentielles et à l'analyse des chaînes de Markov. 

Cet article commencera par les principes fondamentaux d'une matrice diagonale, explorera ce qui rend une matrice diagonalisable et présentera étape par étape le processus de diagonalisation à l'aide d'exemples détaillés. Nous découvrirons également l'algorithme numérique sophistiqué qui permet de traiter efficacement de grandes matrices.

Qu'est-ce qu'une matrice diagonale ?

Une matrice diagonale est une matrice carrée dans laquelle tous les éléments situés en dehors de la diagonale principale sont nuls. 

En notation mathématique, une matrice D est diagonale si D[i,j] = 0 chaque fois que i ≠ j.

L'exemple le plus simple est une matrice diagonale 3×3 :

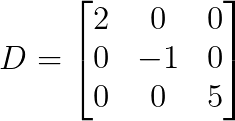
Veuillez noter que tous les éléments, à l'exception des éléments diagonaux, sont égaux à zéro. Qu'est-ce qui rend ces matrices particulières ?

Pourquoi les matrices diagonales sont-elles importantes ?

Les matrices diagonales présentent de nombreux avantages en termes de calcul grâce à leur structure simple :

• Simplicité de la multiplication: Lorsqu'on multiplie des matrices diagonales, on peut multiplier les éléments diagonaux correspondants. Ainsi, la multiplication matricielle-vectorielle ne nécessite que n multiplications au lieu de n² pour les matrices générales.
• s de calcul de puissance: Pour calculer D^n, nous pouvons élever chaque élément diagonal à la puissance n, sans avoir besoin d'effectuer de multiplication matricielle complexe.
• s de calcul inverse: Si tous les éléments diagonaux sont différents de zéro, l'inverse peut être calculé en prenant les inverses des éléments diagonaux, ce qui évite une inversion matricielle coûteuse.
• déterminante: Le déterminant est égal au produit de tous les éléments diagonaux.
• Conditions de stockage: Le stockage passe de^n² à n éléments, ce qui réduit l'utilisation de la mémoire pour les matrices volumineuses.
• s des valeurs propres: Les valeurs propres sont directement visibles sous forme d'entrées diagonales, ce qui simplifie considérablement l'analyse spectrale.
• Résolution de systèmes linéaires: La résolution de Dx = b se réduit à une division élément par élément, transformant ainsi une opération complexe en une opération simple.

Ces avantages informatiques expliquent également pourquoi le processus de diagonalisation est une technique si précieuse en calcul numérique.

Qu'est-ce que la diagonalisation d'une matrice ?

La diagonalisation d'une matrice est le processus qui consiste à trouver une matrice diagonale D et une matrice inversible P telles que :

De manière équivalente, nous pouvons écrire :

Cela démontre que D est similaire à A par un changement de base représenté par P.

D'un point de vue géométrique, la diagonalisation révèle que de nombreuses transformations linéaires peuvent être décomposées en trois étapes :

1. Passer à un système de coordonnées spécial (multiplication par ^P-1)
2. Appliquez une mise à l'échelle simple le long des axes de coordonnées (multiplication par D).
3. Revenez aux coordonnées d'origine (multiplication par P).

Les colonnes de P sont des vecteurs propres de A, tandis que les éléments diagonaux de D sont les valeurs propres correspondantes. Ce lien entre la diagonalisation et le système propre peut être compris comme suit : une matrice est diagonalisable si et seulement si elle possède suffisamment de vecteurs propres linéairement indépendants pour former une base.

Quand une matrice peut-elle être diagonalisée ?

Étant donné que toutes les matrices ne peuvent pas être diagonalisées, nous allons comprendre le théorème de diagonalisation et les conditions de diagonalisation avant d'appliquer cette technique.

Le théorème de la diagonalisation

Le théorème stipule que : Une matrice n×n A est diagonalisable si et seulement si A possède n vecteurs propres linéairement indépendants.

Cela signifie que la diagonalisation dépend entièrement de la structure géométrique de la transformation, plus précisément de l'existence d'une base composée uniquement de vecteurs propres.

Conditions nécessaires et suffisantes

Les conditions pour le processus de diagonalisation sont les suivantes :

1. Ensemble complet des vecteurs propres d': La matrice possède n vecteurs propres linéairement indépendants.
2. La multiplicité géométrique est égale à la multiplicité algébrique: Pour chaque valeur propre λ, la dimension de son espace propre est égale au nombre de fois où λ apparaît comme racine du polynôme caractéristique.
3. Le polynôme minimal possède des facteurs linéaires distincts: Le polynôme minimal se décompose complètement en facteurs linéaires distincts.

Le test le plus pratique consiste à vérifier si chaque valeur propre possède un nombre « suffisant » de vecteurs propres. Si une valeur propre λ apparaît k fois comme racine du polynôme caractéristique, nous avons besoin d'exactement k vecteurs propres linéairement indépendants associés à λ.

Matrices diagonalisables et non diagonalisables

Certains types de matrices sont toujours diagonalisables :

• Matrice symétrique (valeurs propres réelles, vecteurs propres orthogonaux)
• Matrices avec n valeurs propres distinctes (elles ont automatiquement n vecteurs propres indépendants)
• Matrice hermitienne (analogue complexe des matrices symétriques)

Les matrices non diagonalisables courantes sont les suivantes :

• Matrices nilpotentes (telles que les matrices triangulaires supérieures avec des zéros sur la diagonale)
• Blocs de Jordan (matrices avec des valeurs propres répétées mais des vecteurs propres insuffisants)
• Matrices défectueuses (celles qui ne disposent pas d'un ensemble complet de vecteurs propres)

Idées fausses courantes

Avant de poursuivre, abordons quelques idées fausses courantes concernant la diagonalisation :

• Diagonalisation ≠ inversibilité: Il s'agit de propriétés totalement indépendantes. Une matrice peut être diagonalisable mais singulière (ayant zéro comme valeur propre). Si zero est une valeur propre, la matrice n'est pas inversible mais peut tout de même être diagonalisable. De même, une matrice peut être inversible mais non diagonalisable : Une matrice sans valeurs propres nulles (et donc inversible) peut néanmoins ne pas disposer d'un nombre suffisant de vecteurs propres. 
• Diagonalisation ≠ avoir des valeurs propres réelles: Les matrices avec des valeurs propres complexes peuvent toujours être diagonalisables sur les nombres complexes.
• Valeurs propres répétées ≠ non diagonalisable: Les matrices peuvent avoir des valeurs propres répétées et être tout de même diagonalisables si elles ont suffisamment de vecteurs propres.

Jusqu'à présent, nous avons étudié tous les concepts relatifs à la diagonalisation. Vous êtes désormais prêt à vous plonger dans le processus étape par étape de la diagonalisation, illustré par de nombreux exemples.

Processus étape par étape pour la diagonalisation

Examinons étape par étape le processus de diagonalisation d'une matrice.

Étape 1 : Recherche des valeurs propres

Tout d'abord, nous résolvons l'équation caractéristique pour trouver toutes les valeurs propres :

Considérons une matrice 2×2 :

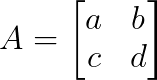
Le polynôme caractéristique est :

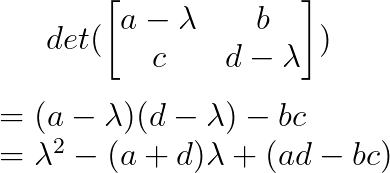
En posant cette équation à zéro et en la résolvant, nous obtenons les valeurs propres. Pour les matrices plus grandes, le processus implique le calcul des déterminants de matrices (n×n), ce qui devient de plus en plus complexe.

Étape 2 : Recherche de vecteurs propres

Pour chaque valeur propre λᵢ, nous résolvons le système afin de trouver les vecteurs propres correspondants :

Cela implique :

1. En substituant λᵢ dans (A — λᵢI)
2. Réduire la matrice obtenue en supprimant les lignes nulles afin de trouver l'espace nul.
3. Exprimer la solution générale en termes de paramètres libres
4. Sélectionner des vecteurs propres spécifiques (généralement avec des composantes entières simples)

Le nombre de vecteurs propres linéairement indépendants pour chaque valeur propre détermine si la diagonalisation est possible.

Étape 3 : Construction de P et D

Une fois que nous avons tous les vecteurs propres :

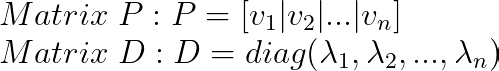
Ici, l'ordre des valeurs est important ; la ième colonne de P doit correspondre à la ième entrée diagonale de D.

Enfin, nous pouvons vérifier la diagonalisation à l'aide de :

1. Calculer ^{P-1 (} ou vérifier que P est inversible)
2. Vérifier que A = ^PDP-1 ou, de manière équivalente, que D = ^P-1AP
3. Vérification que Avᵢ = λᵢvᵢ pour chaque paire vecteur propre-valeur propre

L'ordre des vecteurs propres dans P est arbitraire, mais une fois choisi, il détermine l'ordre des valeurs propres dans D. Des ordres différents donnent des diagonalisation différentes mais équivalentes.

Exemples de diagonalisation élaborés

Examinons différents scénarios pour mieux comprendre le processus de diagonalisation.

Exemple 1 : Matrice avec des valeurs propres distinctes

Considérons la matrice suivante :

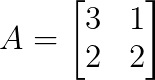
Nous commençons par déterminer les valeurs propres en écrivant le polynôme caractéristique sous la forme suivante :

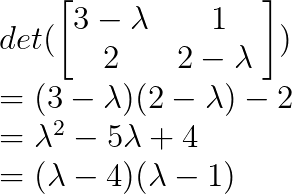
Ainsi, λ₁ = 4 et λ₂ = 1.

Ensuite, nous pouvons trouver les vecteurs propres en substituant des valeurs à λ.

Pour λ₁ = 4 :

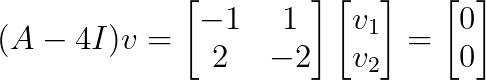
Ceci donne v₁ = [1, 1]ᵀ

En remplaçant λ₂ = 1 :

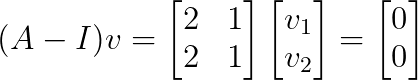
Ceci donne v₂ = [1, -2]ᵀ

Nous pouvons construire la diagonalisation comme suit :

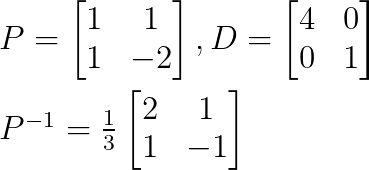
Étant donné que nous avons trouvé toutes les matrices P, D et ^P-1, nous pouvons diagonaliser la matrice d'origine.

Exemple 2 : Matrice avec valeurs propres répétées

Veuillez considérer ce qui suit :

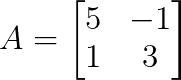
Déterminons les valeurs propres à l'aide du polynôme caractéristique :

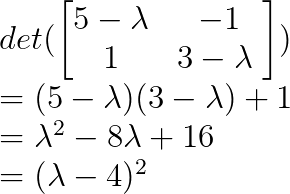
Ainsi, λ = 4 est une valeur propre répétée avec une multiplicité algébrique 2.

Déterminons les vecteurs propres pour λ = 4 :

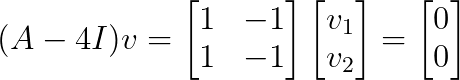
Ce système a un rang 1, ce qui nous donne un espace propre unidimensionnel avec un vecteur de base v = [1, 1]ᵀ.

Étant donné que nous n'avons qu'un seul vecteur propre linéairement indépendant pour une valeur propre de multiplicité 2, cette matrice n'est pas diagonalizable. non diagonalisable.

Exemple 3 : Valeurs propres complexes

Considérons la matrice de rotation :

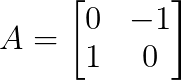
Nous pouvons déterminer les valeurs propres à l'aide du polynôme caractéristique :

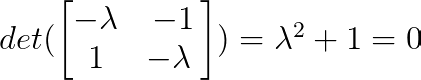
Ainsi, λ₁ = i et λ₂ = -i (où i est l'unité imaginaire).

Ensuite, nous déterminons les vecteurs propres. Pour λ₁ = i :

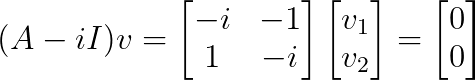
Ceci donne v₁ = [1, -i]ᵀ

Pour λ₂ = -i :

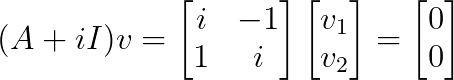
Ceci donne v₂ = [1, i]ᵀ

Il s'agit d'un exemple classique de diagonalisation complexe :

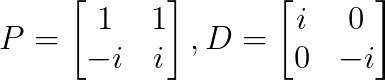
Cette matrice est diagonalisable sur les nombres complexes, mais pas sur les nombres réels.

Méthodes de calcul et considérations numériques

Si les calculs manuels conviennent pour les petites matrices, les applications pratiques nécessitent des algorithmes numériques capables de traiter efficacement de grandes matrices.

L'algorithme QR

L'algorithme QR est la méthode standard utilisée dans les logiciels modernes pour trouver les valeurs propres. Au lieu de résoudre des polynômes caractéristiques (ce qui devient peu pratique pour les matrices de grande taille), il utilise une approche itérative qui révèle progressivement les valeurs propres.

L'algorithme fonctionne par transformations répétées :

1. Décomposer : Aₖ = QₖRₖ (QR decomposition)
2. Forme : Aₖ₊₁ = RₖQₖ
3. Répétez jusqu'à convergence.

À chaque itération, la matrice devient plus triangulaire tout en conservant ses valeurs propres. Finalement, les valeurs propres apparaissent le long de la diagonale. Pour les matrices symétriques, le résultat est une matrice diagonale, ce qui nous donne directement la diagonalisation.

Les implémentations modernes améliorent cet algorithme de base avec :

• Pré-traitement pour réduire le coût de calcul
• Changements qui accélèrent la convergence
• Méthodes permettant d'extraire rapidement les valeurs propres convergentes
• Techniques spéciales pour les paires d'eigenvalues complexes

Conditionnement et stabilité numérique

Tous les problèmes de diagonalisation ne sont pas aussi stables les uns que les autres. Le facteur clé réside dans le degré de « séparation » des vecteurs propres. Lorsque les vecteurs propres pointent dans la même direction, de petites erreurs numériques peuvent entraîner des erreurs importantes dans les résultats.

Cette instabilité se manifeste de plusieurs façons :

• s proches des valeurs propres: Lorsque les valeurs propres sont très proches, leurs vecteurs propres deviennent difficiles à distinguer numériquement.
• Matrices quasi défectueuses: Les matrices qui sont presque non diagonalisables ont des vecteurs propres extrêmement sensibles.
• Erreurs d'arrondi: L'arithmétique informatique peut amplifier de petites erreurs et les transformer en inexactitudes significatives.

Face à ces cas instables, les bibliothèques numériques ont souvent recours à des décompositions alternatives qui sacrifient la simplicité de la forme diagonale au profit d'un meilleur comportement numérique.

Travail avec de grandes matrices

Différentes stratégies s'appliquent en fonction de la taille et de la structure de notre matrice.

Pour les matrices clairsemées (principalement composées de zéros), des algorithmes spécialisés tels que les méthodes de Lanczos ou d'Arnoldi permettent de trouver les valeurs propres sans jamais former la matrice complète. Cette méthode est particulièrement efficace lorsque la matrice est trop volumineuse pour être stockée.

Lorsque nous n'avons besoin que de quelques valeurs propres (comme la plus grande ou la plus petite), les méthodes itératives permettent de les trouver directement sans calculer l'ensemble du spectre.

Pour les problèmes complexes, les algorithmes parallèles répartissent le travail entre plusieurs processeurs, tandis que les méthodes sans matrice évitent de stocker la matrice dans son intégralité, ne nécessitant que la capacité de la multiplier par des vecteurs.

La meilleure approche dépend généralement des besoins spécifiques du problème à résoudre : la structure matricielle, le nombre de valeurs propres requises et la précision nécessaire pour notre application.

Conclusion

La diagonalisation d'une matrice transforme des transformations linéaires complexes en leur forme la plus simple, révélant leur structure à travers des valeurs propres et des vecteurs propres. Nous avons examiné dans quels cas les matrices peuvent être diagonalisées, ce qui nécessite un ensemble complet de vecteurs propres linéairement indépendants, et nous avons suivi le processus systématique permettant de trouver ces décompositions propres.

À travers des exemples concrets, nous avons observé comment des valeurs propres distinctes garantissent la diagonalisation, tandis que des valeurs propres répétées nécessitent une analyse des espaces propres. Nous avons également examiné des cas où la diagonalisation échoue et découvert les méthodes numériques qui rendent la diagonalisation à grande échelle réalisable sur le plan informatique.

Pour approfondir vos connaissances sur les diagonalisation de matrices et leurs applications en science des données, nous vous invitons à vous inscrire à notre cours Algèbre linéaire pour la science des données, où vous maîtriserez ces concepts grâce à des mises en pratique et des exemples concrets.