Matrix Diagonalization: A Comprehensive Guide

Matrix diagonalization is a useful technique in linear algebra that transforms complex matrices into their simplest form, which is a diagonal matrix. Diagonalization is useful across multiple applications in data science, ranging from principal component analysis to solving differential equations and analyzing Markov chains. 

This article will start from the fundamentals of a diagonal matrix, explore what makes a matrix diagonalizable, and walk through the step-by-step process of diagonalization with detailed examples. We will also learn about the sophisticated numerical algorithm that handles large matrices efficiently.

What Is a Diagonal Matrix?

A diagonal matrix is a square matrix where all elements outside the main diagonal are zero. 

In mathematical notation, a matrix D is diagonal if D[i,j] = 0 whenever i ≠ j.

The simplest example is a 3×3 diagonal matrix:

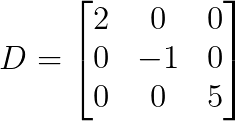
Notice how all elements except for the diagonal elements are zero. So what makes these matrices special?

Why are diagonal matrices important?

Diagonal matrices have multiple computational advantages due to their simple structure:

• Multiplication simplicity: When multiplying diagonal matrices, we can multiply the corresponding diagonal elements. Thus, matrix-vector multiplication requires only n multiplications instead of n² for general matrices.
• Power computation: To compute D^n, we can raise each diagonal element to the nth power, without the need for any complex matrix multiplication.
• Inverse calculation: If all diagonal elements are non-zero, the inverse can be calculated by taking reciprocals of diagonal elements, avoiding expensive matrix inversion.
• Determinant: The determinant equals the product of all diagonal elements.
• Storage requirements: Storage drops from n^² to n elements, thereby reducing the memory usage for large matrices.
• Eigenvalues: Eigenvalues are directly visible as the diagonal entries, making spectral analysis trivial.
• Solving linear systems: Solving Dx = b reduces to element-wise division, converting a complex operation into a straightforward one.

These computational advantages also explain why the process of diagonalization is such a valuable technique in numerical computing.

What Is Matrix Diagonalization?

Matrix diagonalization is the process of finding a diagonal matrix D and an invertible matrix P such that:

Equivalently, we can write:

This shows that D is similar to A through a change of basis represented by P.

Geometrically, diagonalization reveals that many linear transformations can be decomposed into three steps:

1. Change to a special coordinate system (multiplication by P^-1)
2. Apply a simple scaling along coordinate axes (multiplication by D)
3. Change back to the original coordinates (multiplication by P)

The columns of P are eigenvectors of A, while the diagonal entries of D are the corresponding eigenvalues. This connection between diagonalization and the eigensystem can be understood as: a matrix is diagonalizable if and only if it has enough linearly independent eigenvectors to form a basis.

When Can a Matrix Be Diagonalized?

Since not all matrices can be diagonalized, let’s understand the diagonalization theorem and the conditions for diagonalizability before applying the technique.

The diagonalization theorem

The theorem states: An n×n matrix A is diagonalizable if and only if A has n linearly independent eigenvectors.

It means that diagonalizability depends entirely on the geometric structure of the transformation, specifically, whether there exists a basis consisting entirely of eigenvectors.

Necessary and sufficient conditions

The conditions for the diagonalization process are as follows:

1. Full set of eigenvectors: The matrix has n linearly independent eigenvectors.
2. Geometric multiplicity equals algebraic multiplicity: For each eigenvalue λ, the dimension of its eigenspace equals the number of times λ appears as a root of the characteristic polynomial.
3. Minimal polynomial has distinct linear factors: The minimal polynomial splits completely into distinct linear factors.

The most practical test involves checking whether each eigenvalue has “enough” eigenvectors. If an eigenvalue λ appears k times as a root of the characteristic polynomial, we need exactly k linearly independent eigenvectors associated with λ.

Diagonalizable vs. non-diagonalizable matrices

Certain matrix types are always diagonalizable:

• Symmetric matrices (real eigenvalues, orthogonal eigenvectors)
• Matrices with n distinct eigenvalues (they automatically have n independent eigenvectors)
• Hermitian matrices (complex analogue of symmetric matrices)

Common non-diagonalizable matrices are:

• Nilpotent matrices (like upper triangular matrices with zeros on the diagonal)
• Jordan blocks (matrices with repeated eigenvalues but insufficient eigenvectors)
• Defective matrices (those lacking a complete set of eigenvectors)

Common misconceptions

Before moving forward, let’s address some common misconceptions regarding diagonalizability:

• Diagonalizability ≠ invertibility: These are completely independent properties. A matrix can be diagonalizable but singular (having zero as an eigenvalue). If zero is an eigenvalue, the matrix is not invertible but can still be diagonalizable. Similarly, a matrix can be invertible but non-diagonalizable: A matrix with no zero eigenvalues (hence invertible) might still lack enough eigenvectors. 
• Diagonalizability ≠ having real eigenvalues: Matrices with complex eigenvalues can still be diagonalizable over the complex numbers.
• Repeated eigenvalues ≠ non-diagonalizable: Matrices can have repeated eigenvalues and still be diagonalizable if they have enough eigenvectors.

So far, we have learned all the concepts surrounding the Diagonalization. You’re more than ready to dive into the step-by-step process for diagonalization, along with multiple examples.

Step-by-Step Process for Diagonalization

Let’s walk through the process of diagonalizing a matrix in a step-by-step fashion.

Step 1: Finding eigenvalues

First, we solve the characteristic equation to find all eigenvalues:

Considering a 2×2 matrix:

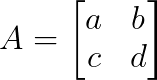
The characteristic polynomial is:

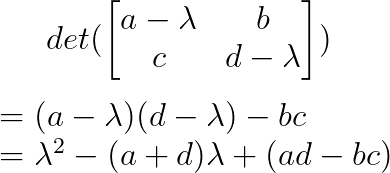
Setting this equal to zero and solving gives us the eigenvalues. For larger matrices, the process involves computing determinants of (n×n) matrices, which becomes increasingly complex.

Step 2: Finding eigenvectors

For each eigenvalue λᵢ, we solve the system to find the corresponding eigenvectors:

This involves:

1. Substituting λᵢ into (A — λᵢI)
2. Row reducing the resulting matrix to find the null space
3. Expressing the general solution in terms of free parameters
4. Choosing specific eigenvectors (typically with simple integer components)

The number of linearly independent eigenvectors for each eigenvalue determines whether diagonalization is possible.

Step 3: Constructing P and D

Once we have all the eigenvectors:

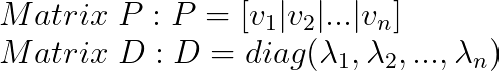
Here, the order of the value matters; the ith column of P must correspond to the ith diagonal entry of D.

Finally, we can verify the diagonalization through:

1. Computing P^-1 (or check that P is invertible)
2. Verifying that A = PDP^-1 or equivalently D = P^-1AP
3. Checking that Avᵢ = λᵢvᵢ for each eigenvector-eigenvalue pair

The order of eigenvectors in P is arbitrary, but once chosen, it determines the order of eigenvalues in D. Different orderings yield different but equivalent diagonalizations.

Worked-out Diagonalization Examples

Let’s work through different scenarios to solidify our understanding of the diagonalization process.

Example 1: Matrix with distinct eigenvalues

Consider the matrix:

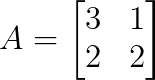
We work through the first step of finding the eigenvalues by writing the characteristic polynomial as,

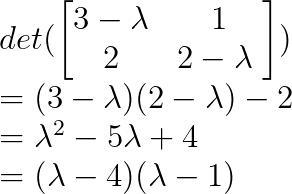
So λ₁ = 4 and λ₂ = 1.

Next, we can find the eigenvectors by substituting values for λ.

For λ₁ = 4:

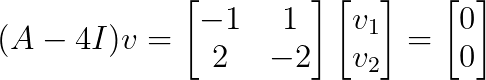
This gives v₁ = [1, 1]ᵀ

Substituting λ₂ = 1:

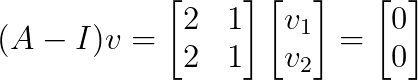
This gives v₂ = [1, -2]ᵀ

We can construct the diagonalization as:

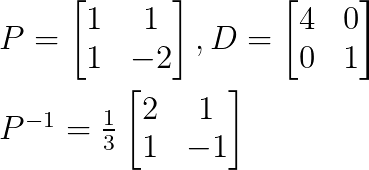
Since we have found all matrices P, D, and P^-1, we can diagonalize the original matrix.

Example 2: Matrix with repeated eigenvalues

Consider:

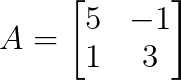
Let’s find the eigenvalues through the characteristic polynomial:

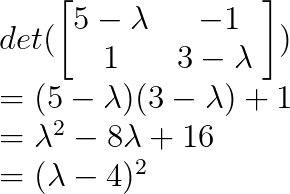
So λ = 4 is a repeated eigenvalue with algebraic multiplicity 2.

Let’s find the eigenvectors for λ = 4:

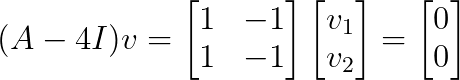
This system has rank 1, giving us a 1-dimensional eigenspace with basis vector v = [1, 1]ᵀ.

Since we have only one linearly independent eigenvector for an eigenvalue of multiplicity 2, this matrix is not diagonalizable.

Example 3: Complex eigenvalues

Consider the rotation matrix:

We can find the eigenvalues through the characteristic polynomial:

So λ₁ = i and λ₂ = -i (where i is the imaginary unit).

Next, we find the eigenvectors. For λ₁ = i:

This gives v₁ = [1, -i]ᵀ

For λ₂ = -i:

This gives v₂ = [1, i]ᵀ

This is a classic example of a complex diagonalization:

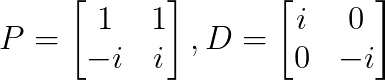
This matrix is diagonalizable over the complex numbers but not over the real numbers.

Computational Methods and Numerical Considerations

While hand calculations work well for small matrices, practical applications require numerical algorithms that can handle large matrices efficiently.

The QR algorithm

The QR algorithm is the standard method for finding eigenvalues in modern software. Instead of solving characteristic polynomials (which becomes impractical for large matrices), it uses an iterative approach that gradually reveals the eigenvalues.

The algorithm works through repeated transformations:

1. Decompose: Aₖ = QₖRₖ (QR decomposition)
2. Form: Aₖ₊₁ = RₖQₖ
3. Repeat until convergence

With each iteration, the matrix becomes more triangular while preserving its eigenvalues. Eventually, the eigenvalues appear along the diagonal. For symmetric matrices, the result is a diagonal matrix, giving us the diagonalization directly.

Modern implementations enhance this basic algorithm with:

• Pre-processing to reduce computational cost
• Shifts that speed up convergence
• Methods to extract converged eigenvalues early
• Special techniques for complex eigenvalue pairs

Conditioning and numerical stability

Not all diagonalization problems are equally stable. The key factor is how “separated” the eigenvectors are. When eigenvectors point in nearly the same direction, small numerical errors can cause large mistakes in the results.

This instability appears in several ways:

• Close eigenvalues: When eigenvalues are very similar, their eigenvectors become hard to distinguish numerically.
• Near-defective matrices: Matrices that are almost non-diagonalizable have extremely sensitive eigenvectors.
• Round-off errors: Computer arithmetic can amplify small errors into significant inaccuracies

When facing these unstable cases, numerical libraries often use alternative decompositions that sacrifice the simplicity of the diagonal form for improved numerical behavior.

Working with large matrices

Different strategies apply depending on the size and structure of our matrix.

For sparse matrices (mostly zeros), specialized algorithms like Lanczos or Arnoldi methods find eigenvalues without ever forming the full matrix. This works well when the matrix is too large to store.

When we need only a few eigenvalues (like the largest or smallest), iterative methods can find them directly without computing the entire spectrum.

For large problems, parallel algorithms split the work across multiple processors, while matrix-free methods avoid storing the matrix entirely, needing only the ability to multiply it by vectors.

The best approach generally depends on the specific needs of the problem being solved: the matrix structure, the number of eigenvalues required, and the accuracy needed for our application.

Conclusion

Matrix diagonalization transforms complex linear transformations into their simplest form, revealing their structure through eigenvalues and eigenvectors. We’ve explored when matrices can be diagonalized, requiring a complete set of linearly independent eigenvectors, and walked through the systematic process of finding these eigendecompositions.

Through practical examples, we’ve seen how distinct eigenvalues guarantee diagonalizability, while repeated eigenvalues require an analysis of eigenspaces. We’ve also examined cases where diagonalization fails, and learned about the numerical methods that make large-scale diagonalization computationally feasible.

To further explore matrix diagonalizations and their applications in data science, consider enrolling in our Linear Algebra for Data Science course, where you’ll master these concepts through hands-on implementations and real-world examples.