Diagonalização da matriz: Um guia completo

A diagonalização de matrizes é uma técnica útil em álgebra linear que transforma matrizes complexas na sua forma mais simples, que é uma matriz diagonal. A diagonalização é útil em várias aplicações na ciência de dados, desde a análise de componentes principais até a resolução de equações diferenciais e a análise de cadeias de Markov. 

Este artigo vai começar com o básico sobre matrizes diagonais, ver o que faz uma matriz ser diagonalizável e explicar passo a passo como fazer a diagonalização com exemplos detalhados. Também vamos aprender sobre o algoritmo numérico sofisticado que lida com grandes matrizes de forma eficiente.

O que é uma matriz diagonal?

Uma matriz diagonal é uma matriz quadrada em que todos os elementos fora da diagonal principal são zero. 

Na notação matemática, uma matriz D é diagonal se D[i,j] = 0 sempre que i ≠ j.

O exemplo mais simples é uma matriz diagonal 3×3:

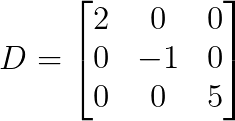
Repara que todos os elementos, exceto os diagonais, são zero. Então, o que torna essas matrizes especiais?

Por que as matrizes diagonais são importantes?

As matrizes diagonais têm várias vantagens computacionais por causa da sua estrutura simples:

• Simplicidade da multiplicação: Quando multiplicamos matrizes diagonais, podemos multiplicar os elementos diagonais correspondentes. Então, a multiplicação de matriz por vetor só precisa de n multiplicações em vez de n² para matrizes gerais.
• Cálculo de potência: Para calcular D^n, podemos elevar cada elemento diagonal à potência n, sem precisar de nenhuma multiplicação complexa de matrizes.
• Cálculo inverso: Se todos os elementos diagonais forem diferentes de zero, a inversa pode ser calculada pegando os inversos dos elementos diagonais, evitando a inversão da matriz, que é bem complicada.
• e determinante: O determinante é igual ao produto de todos os elementos diagonais.
• Requisitos de armazenamento: O armazenamento cai de^n² para n elementos, reduzindo assim o uso de memória para matrizes grandes.
• Valores próprios: Os valores próprios são visíveis diretamente como entradas na diagonal, o que facilita a análise espectral.
• Resolvendo sistemas lineares: Resolver Dx = b é só dividir elemento por elemento, transformando uma operação complicada em uma bem simples.

Essas vantagens computacionais também explicam por que o processo de diagonalização é uma técnica tão valiosa na computação numérica.

O que é diagonalização de matrizes?

A diagonalização de matrizes é o processo de encontrar uma matriz diagonal D e uma matriz invertível P de forma que:

Da mesma forma, podemos escrever:

Isso mostra que D é parecido com A através de uma mudança de base representada por P.

Geometricamente, a diagonalização mostra que muitas transformações lineares podem ser divididas em três passos:

1. Mudança para um sistema de coordenadas especial (multiplicação por ^P-1)
2. Faça uma escala simples nos eixos de coordenadas (multiplique por D).
3. Voltar às coordenadas originais (multiplicar por P)

As colunas de P são vetores próprios de A, enquanto as entradas diagonais de D são os valores próprios correspondentes. Essa conexão entre diagonalização e o sistema de eigenvectors pode ser entendida assim: uma matriz é diagonalizável se e somente se tiver eigenvectors linearmente independentes suficientes para formar uma base.

Quando uma matriz pode ser diagonalizada?

Como nem todas as matrizes podem ser diagonalizadas, vamos entender o teorema da diagonalização e as condições para diagonalizabilidade antes de aplicar a técnica.

O teorema da diagonalização

O teorema diz que: Uma matriz n×n A é diagonalizável se e somente se A tem n vetores próprios linearmente independentes.

Isso quer dizer que a diagonalizabilidade depende totalmente da estrutura geométrica da transformação, mais especificamente, se existe uma base composta só por vetores próprios.

Condições necessárias e suficientes

As condições para o processo de diagonalização são as seguintes:

1. Conjunto completo de vetores próprios: A matriz tem n vetores próprios linearmente independentes.
2. A multiplicidade geométrica é igual à multiplicidade algébrica: Para cada autovalor λ, a dimensão do seu espaço próprio é igual ao número de vezes que λ aparece como raiz do polinômio característico.
3. O polinômio mínimo tem fatores lineares distintos: O polinômio mínimo se divide completamente em fatores lineares distintos.

O teste mais prático é ver se cada autovalor tem “vectores próprios suficientes”. Se um autovalor λ aparece k vezes como raiz do polinômio característico, precisamos exatamente de k vetores próprios linearmente independentes associados a λ.

Matrizes diagonalizáveis vs. não diagonalizáveis

Alguns tipos de matrizes são sempre diagonalizáveis:

• Matrizes simétricas (autovalores reais, autovetores ortogonais)
• Matrizes com n valores próprios diferentes (elas automaticamente têm n vetores próprios independentes)
• Matrizes hermitianas (análogo complexo das matrizes simétricas)

Matrizes não diagonalizáveis comuns são:

• Matrizes nilpotentes (como matrizes triangulares superiores com zeros na diagonal)
• Blocos de Jordan (matrizes com autovalores repetidos, mas autovetores insuficientes)
• Matrizes defeituosas (aquelas que não possuem um conjunto completo de vetores próprios)

Equívocos comuns

Antes de continuar, vamos esclarecer alguns equívocos comuns sobre diagonalizabilidade:

• Diagonalizabilidade ≠ invertibilidade: São propriedades totalmente independentes. Uma matriz pode ser diagonalizável, mas singular (tendo zero como valor próprio). Se zero é um valor próprio, a matriz não é invertível, mas ainda pode ser diagonalizável. Da mesma forma, uma matriz pode ser invertível, mas não diagonalizável: Uma matriz sem valores próprios zero (portanto invertível) ainda pode não ter vetores próprios suficientes. 
• Diagonalizabilidade ≠ ter valores próprios reais: Matrizes com valores próprios complexos ainda podem ser diagonalizáveis sobre os números complexos.
• Valores próprios repetidos ≠ não diagonalizáveis: As matrizes podem ter valores próprios repetidos e ainda assim ser diagonalizáveis se tiverem vetores próprios suficientes.

Até agora, a gente aprendeu todos os conceitos relacionados à diagonalização. Você está mais do que pronto para mergulhar no processo passo a passo da diagonalização, com vários exemplos.

Processo passo a passo para diagonalização

Vamos ver como é que se diagonaliza uma matriz, passo a passo.

Passo 1: Encontrando valores próprios

Primeiro, vamos resolver a equação característica pra achar todos os autovalores:

Pensa numa matriz 2×2:

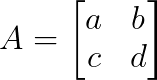
O polinômio característico é:

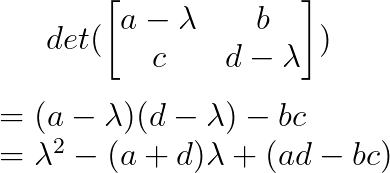
Colocando isso igual a zero e resolvendo, a gente consegue os autovalores. Para matrizes maiores, o processo envolve calcular determinantes de matrizes (n×n), o que fica cada vez mais complicado.

Passo 2: Encontrando vetores próprios

Para cada autovalor λᵢ, resolvemos o sistema para encontrar os autovetores correspondentes:

Isso envolve:

1. Substituindo λᵢ em (A — λᵢI)
2. Reduzindo as linhas da matriz resultante para encontrar o espaço nulo
3. Expressando a solução geral em termos de parâmetros livres
4. Escolhendo vetores próprios específicos (normalmente com componentes inteiros simples)

O número de vetores próprios linearmente independentes para cada valor próprio determina se a diagonalização é possível.

Passo 3: Construindo P e D

Depois de termos todos os vetores próprios:

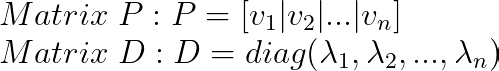
Aqui, a ordem dos valores é importante; a coluna i-ésima de P precisa corresponder à entrada diagonal i-ésima de D.

Por fim, podemos verificar a diagonalização através de:

1. Calcular ^{P-1 (} ou ver se P é invertível)
2. Verificando se A = ^PDP-1 ou, se for o mesmo, D = ^P-1AP
3. Verificando se Avᵢ = λᵢvᵢ para cada par vetor próprio-valor próprio

A ordem dos vetores próprios em P é aleatória, mas, uma vez escolhida, determina a ordem dos valores próprios em D. Ordenações diferentes resultam em diagonalizações diferentes, mas equivalentes.

Exemplos de diagonalização resolvidos

Vamos ver alguns cenários diferentes pra entender melhor o processo de diagonalização.

Exemplo 1: Matriz com valores próprios diferentes

Olha só essa matriz:

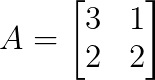
A gente começa encontrando os autovalores, escrevendo o polinômio característico assim:

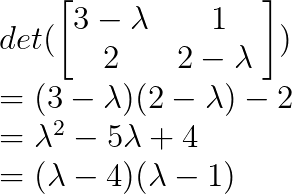
Então, λ₁ = 4 e λ₂ = 1.

Depois, dá pra achar os vetores próprios substituindo os valores de λ.

Para λ₁ = 4:

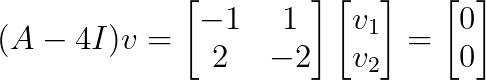
Isso dá v₁ = [1, 1]ᵀ

Substituindo λ₂ = 1:

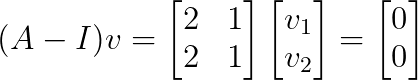
Isso dá v₂ = [1, -2]ᵀ

A gente pode fazer a diagonalização assim:

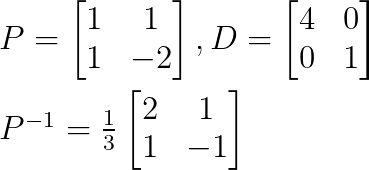
Como já achamos todas as matrizes P, D e ^P-1, podemos diagonalizar a matriz original.

Exemplo 2: Matriz com valores próprios repetidos

Pense nisso:

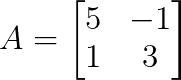
Vamos achar os autovalores usando o polinômio característico:

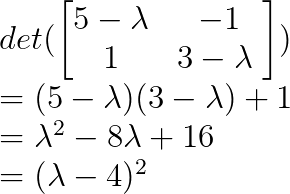
Então, λ = 4 é um valor próprio repetido com multiplicidade algébrica 2.

Vamos achar os vetores próprios para λ = 4:

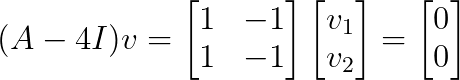
Esse sistema tem classificação 1, o que nos dá um espaço próprio unidimensional com vetor base v = [1, 1]ᵀ.

Como só temos um vetor próprio linearmente independente para um valor próprio de multiplicidade 2, essa matriz não é diagonalizável. não diagonalizável.

Exemplo 3: Valores próprios complexos

Pensa na matriz de rotação:

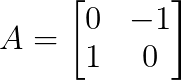
A gente consegue achar os autovalores usando o polinômio característico:

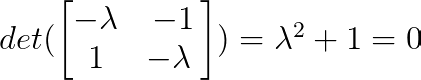
Então, λ₁ = i e λ₂ = -i (onde i é a unidade imaginária).

Depois, a gente encontra os vetores próprios. Para λ₁ = i:

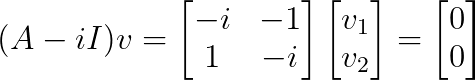
Isso dá v₁ = [1, -i]ᵀ

Para λ₂ = -i:

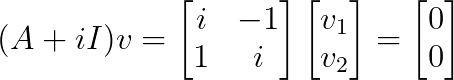
Isso dá v₂ = [1, i]ᵀ

Esse é um exemplo clássico de diagonalização complexa:

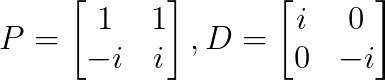
Essa matriz é diagonalizável sobre os números complexos, mas não sobre os números reais.

Métodos computacionais e considerações numéricas

Embora os cálculos manuais funcionem bem para matrizes pequenas, as aplicações práticas precisam de algoritmos numéricos que possam lidar com matrizes grandes de forma eficiente.

O algoritmo QR

O algoritmo QR é o jeito padrão de achar valores próprios em programas modernos. Em vez de resolver polinômios característicos (o que fica complicado para matrizes grandes), ele usa uma abordagem iterativa que vai mostrando os autovalores aos poucos.

O algoritmo funciona através de transformações repetidas:

1. Decompor: Aₖ = QₖRₖ (decomposição QR)
2. Formulário: Aₖ₊₁ = RₖQₖ
3. Repita até que tudo se encaixe.

A cada repetição, a matriz fica mais triangular, mas mantém seus valores próprios. No final, os valores próprios aparecem na diagonal. Para matrizes simétricas, o resultado é uma matriz diagonal, que nos dá diretamente a diagonalização.

As implementações modernas melhoram esse algoritmo básico com:

• Pré-processamento para reduzir o custo computacional
• Mudanças que aceleram a convergência
• Métodos para extrair rapidamente valores próprios convergentes
• Técnicas especiais para pares complexos de valores próprios

Condicionamento e estabilidade numérica

Nem todos os problemas de diagonalização são igualmente estáveis. O fator principal é o quanto os vetores próprios estão “separados”. Quando os vetores próprios apontam quase na mesma direção, pequenos erros numéricos podem causar grandes erros nos resultados.

Essa instabilidade aparece de várias maneiras:

• Eigenvalues próximos: Quando os autovalores são muito parecidos, os autovetores ficam difíceis de distinguir numericamente.
• Matrizes quase defeituosas: Matrizes que são quase não diagonalizáveis têm vetores próprios super sensíveis.
• Erros de arredondamento: A aritmética computacional pode transformar pequenos erros em imprecisões significativas.

Quando a gente se depara com esses casos instáveis, as bibliotecas numéricas geralmente usam decomposições alternativas que sacrificam a simplicidade da forma diagonal para melhorar o comportamento numérico.

Trabalhando com grandes matrizes

A gente usa estratégias diferentes dependendo do tamanho e da estrutura da nossa matriz.

Para matrizes esparsas (principalmente zeros), algoritmos especializados como os métodos Lanczos ou Arnoldi encontram valores próprios sem nunca formar a matriz completa. Isso funciona bem quando a matriz é muito grande pra guardar.

Quando precisamos apenas de alguns autovalores (como o maior ou o menor), métodos iterativos podem encontrá-los diretamente, sem calcular todo o espectro.

Para problemas grandes, os algoritmos paralelos dividem o trabalho entre vários processadores, enquanto os métodos sem matrizes evitam armazenar a matriz inteira, precisando só da capacidade de multiplicá-la por vetores.

A melhor abordagem geralmente depende das necessidades específicas do problema que estamos tentando resolver: a estrutura da matriz, o número de valores próprios necessários e a precisão que precisamos para a nossa aplicação.

Conclusão

A diagonalização de matrizes transforma transformações lineares complexas na sua forma mais simples, mostrando a sua estrutura através dos valores próprios e vetores próprios. A gente viu quando as matrizes podem ser diagonalizadas, precisando de um conjunto completo de vetores próprios linearmente independentes, e deu uma olhada no processo sistemático de encontrar essas decomposições próprias.

Com exemplos práticos, vimos como valores próprios diferentes garantem a diagonalizabilidade, enquanto valores próprios repetidos precisam de uma análise dos espaços próprios. Também vimos casos em que a diagonalização não dá certo e aprendemos sobre os métodos numéricos que tornam a diagonalização em grande escala viável em termos de computação.

Para saber mais sobre diagonalizações de matrizes e como elas podem ajudar na ciência de dados, dá uma olhada no nosso curso Álgebra Linear para Ciência de Dados, onde você vai entender tudo isso com exemplos práticos e do mundo real.