Introducción a los autocodificadores: De lo básico a las aplicaciones avanzadas en PyTorch

Las redes neuronales feedforward tradicionales pueden ser estupendas para realizar tareas como la clasificación y la regresión, pero ¿y si quisiéramos aplicar soluciones como la eliminación de ruido de la señal o la detección de anomalías? Una forma de hacerlo es utilizando Autocodificadores.

Este tutorial proporciona una introducción práctica a los Autoencoders, incluyendo un ejemplo práctico en PyTorch y algunos posibles casos de uso.

Puedes seguirlo en este libro de trabajo de DataLab con todo el código del tutorial.

¿Qué son los autocodificadores?

Los autocodificadores son un tipo especial de red neuronal directa no supervisada (¡no necesita etiquetas!). La principal aplicación de los Autocodificadores es captar con precisión los aspectos clave de los datos proporcionados para ofrecer una versión comprimida de los datos de entrada, generar datos sintéticos realistas o señalar anomalías.

Los autocodificadores se componen de 2 redes neuronales totalmente conectadas de tipo feedforward (Figura 1):

• Codificador: comprime los datos de entrada para eliminar cualquier forma de ruido y genera un espacio latente/cuello de botella. Por tanto, las dimensiones de la red neuronal de salida son menores que las de entrada y pueden ajustarse como hiperparámetro para decidir cuánto debe tener de pérdida nuestra compresión.
• Decodificador: haciendo uso únicamente de la representación comprimida de los datos del espacio latente, intenta reconstruir con la mayor fidelidad posible los datos de entrada originales (la arquitectura de esta red neuronal es, por tanto, generalmente una imagen especular del codificador). La "bondad" de la predicción puede medirse calculando el error de reconstrucción entre los datos de entrada y de salida mediante una función de pérdida.

Repitiendo iterativamente este proceso de pasar datos por el codificador y el descodificador y medir el error para afinar los parámetros mediante retropropagación, el Autocodificador puede, con el tiempo, trabajar correctamente con formas de datos extremadamente difíciles.

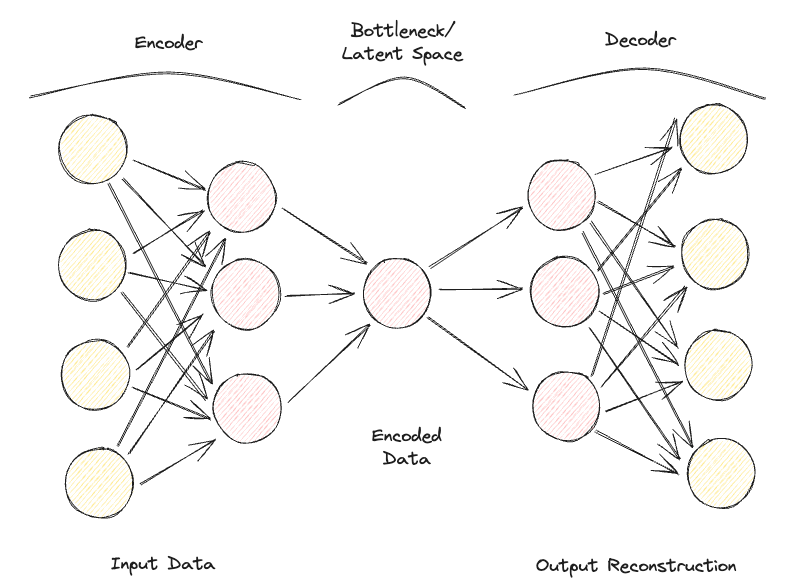
Figura 1: Arquitectura del autocodificador (Imagen del autor).

Si a un Autoencoder se le proporciona un conjunto de características de entrada completamente independientes entre sí, entonces sería realmente difícil para el modelo encontrar una buena representación de menor dimensión sin perder una gran cantidad de información (compresión con pérdidas).

Por tanto, los autocodificadores también pueden considerarse una técnica de reducción de la dimensionalidad, que, en comparación con las técnicas tradicionales, como el Análisis de Componentes Principales (ACP), puede hacer uso de transformaciones no lineales para proyectar los datos en un espacio de menor dimensión. Si te interesa saber más sobre otras técnicas de extracción de rasgos, tienes información adicional en este tutorial de extracción de rasgos...

Además, en comparación con los algoritmos estándar de compresión de datos, como gzpi, los Autocodificadores no pueden utilizarse como algoritmos de compresión de uso general, sino que están diseñados a mano para funcionar mejor sólo con datos similares en los que han sido entrenados.

Algunos de los hiperparámetros más comunes que se pueden ajustar al optimizar tu Autoencoder son:

• El número de capas de las redes neuronales Codificador y Decodificador
• El número de nodos de cada una de estas capas
• La función de pérdida que se utilizará en el proceso de optimización (por ejemplo, entropía cruzada binaria o error cuadrático medio)
• El tamaño del espacio latente (cuanto menor sea, mayor será la compresión, actuando, por tanto, como mecanismo de regularización)

Por último, los autocodificadores pueden diseñarse para trabajar con distintos tipos de datos, como datos tabulares, de series temporales o de imágenes, y pueden, por tanto, diseñarse para utilizar distintas capas, como capas convolucionales, para el análisis de imágenes.

Lo ideal es que un autocodificador bien entrenado responda lo suficiente como para adaptarse a los datos de entrada y dar una respuesta a medida, pero no tanto como para limitarse a imitar los datos de entrada y no ser capaz de generalizar con datos no vistos (por tanto, sobreajuste).

Tipos de autocodificadores

A lo largo de los años, se han desarrollado distintos tipos de Autocodificadores:

• Autocodificador incompleto
• Autocodificador disperso
• Autocodificador contractivo
• Autoencoder de eliminación de ruido
• Autocodificador convolucional
• Autocodificador variacional

Exploremos cada uno de ellos con más detalle.

Autocodificador incompleto

Es la versión más sencilla de un autocodificador. En este caso, no tenemos un mecanismo de regularización explícito, pero nos aseguramos de que el tamaño del cuello de botella sea siempre inferior al tamaño de entrada original para evitar el sobreajuste. Este tipo de configuración se suele utilizar como técnica de reducción de la dimensionalidad (más potente que el ACP, ya que también es capaz de captar las no linealidades de los datos).

Autocodificador disperso

Un autocodificador disperso es bastante similar a un autocodificador incompleto, pero su principal diferencia radica en cómo se aplica la regularización. De hecho, con los Autocodificadores dispersos, no tenemos que reducir necesariamente las dimensiones del cuello de botella, sino que utilizamos una función de pérdida que intenta penalizar al modelo por utilizar todas sus neuronas en las distintas capas ocultas (Figura 2).

Esta penalización se conoce comúnmente como función de sparsity, y es bastante diferente de las técnicas de regularización tradicionales, ya que no se centra en penalizar el tamaño de los pesos, sino el número de nodos activados.

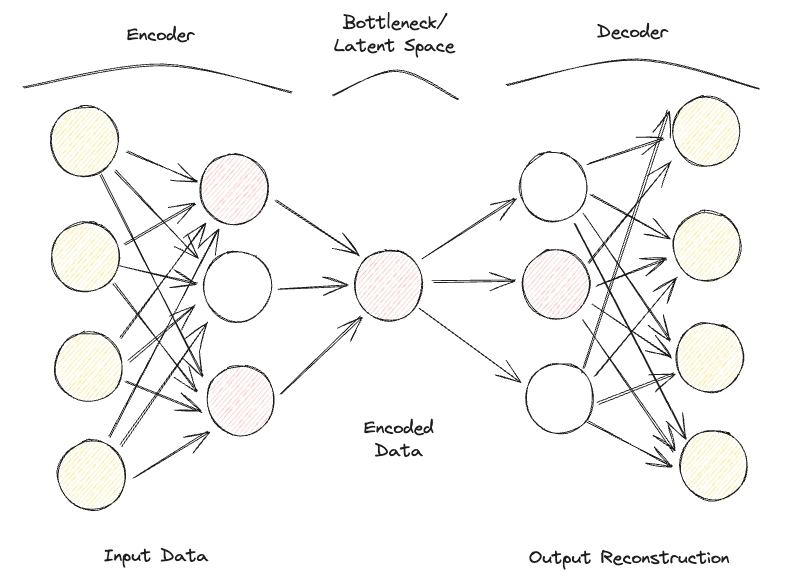
De este modo, distintos nodos podrían especializarse para distintos tipos de entrada y activarse/desactivarse en función de las particularidades de los datos de entrada. Esta restricción de sparsity puede inducirse utilizando la Regularización L1 y la divergencia KL, evitando eficazmente que el modelo se ajuste en exceso.

Autocodificador contractivo

La idea principal de los Autocodificadores Contractivos es que, dadas unas entradas similares, su representación comprimida debe ser bastante parecida (las vecindades de las entradas deben contraerse en vecindades pequeñas de las salidas). En términos matemáticos, esto puede reforzarse manteniendo pequeñas las activaciones de la capa oculta de entrada cuando se alimentan entradas similares.

Autoencoder de eliminación de ruido

Con los autocodificadores de eliminación de ruido, la entrada y la salida del modelo ya no son iguales. Por ejemplo, se podría alimentar al modelo con algunas imágenes corruptas de baja resolución y trabajar para que la salida mejore la calidad de las imágenes. Para evaluar el rendimiento del modelo y mejorarlo con el tiempo, necesitaríamos disponer de algún tipo de imagen limpia etiquetada para compararla con la predicción del modelo.

Autocodificador convolucional

Para trabajar con datos de imagen, los Autocodificadores Convolucionales sustituyen las redes neuronales tradicionales de avance por Redes Neuronales Convolucionales, tanto para el paso del codificador como del decodificador. Actualizando el tipo de función de pérdida, etc., también se puede hacer este tipo de Autoencoder, por ejemplo, Sparse o Denoising, según los requisitos de tu caso de uso.

Autocodificador variacional

En todos los tipos de Autocodificador considerados hasta ahora, el codificador emite un único valor para cada dimensión implicada. Con los Autocodificadores Variacionales (VAE), hacemos que este proceso sea más bien probabilístico, creando una distribución de probabilidad para cada dimensión. A continuación, el descodificador puede muestrear un valor de cada distribución que describa las distintas dimensiones y construir el vector de entrada, que puede utilizarse para reconstruir los datos de entrada originales.

Una de las principales aplicaciones de los Autocodificadores Variacionales es para tareas generativas. De hecho, el muestreo del modelo latente a partir de distribuciones puede permitir al descodificador crear nuevas formas de salidas que antes no eran posibles con un enfoque determinista.

Si te interesa probar en línea un Autoencoder Variacional entrenado en el conjunto de datos MNIST, puedes encontrar un ejemplo en vivo.

Ejemplo práctico de autocodificador

Ahora estamos preparados para hacer una demostración práctica de cómo pueden utilizarse los Autocodificadores para reducir la dimensionalidad. Nuestro marco de Aprendizaje Profundo elegido para este ejercicio va a ser PyTorch.

Para esta demostración se va a utilizar el conjunto de datos de Kaggle Rain in Australia. Todo el código de este artículo está disponible en este libro de trabajo de DataLab.

En primer lugar, importamos todas las bibliotecas necesarias y eliminamos los valores que faltan y las columnas no numéricas (Figura 3).

import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, LabelEncoder
from mpl_toolkits.mplot3d import Axes3D

df = pd.read_csv("../input/weather-dataset-rattle-package/weatherAUS.csv")
df = df.drop(['Date', 'Location', 'WindDir9am',
             'WindGustDir', 'WindDir3pm'], axis=1)
df = df.dropna(how = 'any')
df.loc[df['RainToday'] == 'No', 'RainToday'] = 0
df.loc[df['RainToday'] == 'Yes', 'RainToday'] = 1
df.head()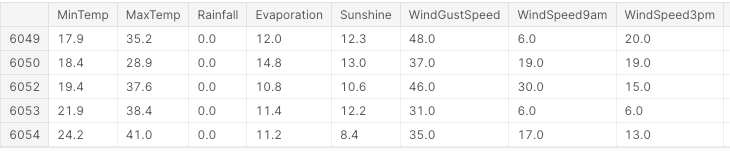

Figura 3: Muestra de columnas del conjunto de datos (Imagen del autor).

Llegados a este punto, estamos preparados para dividir los datos en características y etiquetas, normalizar las características y convertir las etiquetas a un formato numérico.

En este caso, tenemos un conjunto de características inicial compuesto por 17 columnas. El objetivo general del análisis sería entonces predecir correctamente si va a llover al día siguiente o no.

X, Y = df.drop('RainTomorrow', axis=1, inplace=False), df[['RainTomorrow']]
# Normalizing Data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Converting to PyTorch tensor
X_tensor = torch.FloatTensor(X_scaled)

# Converting string labels to numerical labels
label_encoder = LabelEncoder()
Y_numerical = label_encoder.fit_transform(Y.values.ravel())

En PyTorch, ahora podemos definir el modelo Autoencoder como una clase y especificar los modelos codificador y decodificador con dos capas lineales.

# Defining Autoencoder model
class Autoencoder(nn.Module):
   def __init__(self, input_size, encoding_dim):
       super(Autoencoder, self).__init__()
       self.encoder = nn.Sequential(
           nn.Linear(input_size, 16),
           nn.ReLU(),
           nn.Linear(16, encoding_dim),
           nn.ReLU()
       )
       self.decoder = nn.Sequential(
           nn.Linear(encoding_dim, 16),
           nn.ReLU(),
           nn.Linear(16, input_size),
           nn.Sigmoid()
       )

   def forward(self, x):
       x = self.encoder(x)
       x = self.decoder(x)
       return x

Ahora que el modelo está configurado, podemos proceder a especificar que nuestras dimensiones de codificación sean iguales a 3 (para facilitar su trazado más adelante) y ejecutar el proceso de entrenamiento.

# Setting random seed for reproducibility
torch.manual_seed(42)

input_size = X.shape[1]  # Number of input features
encoding_dim = 3  # Desired number of output dimensions
model = Autoencoder(input_size, encoding_dim)

# Loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)

# Training the autoencoder
num_epochs = 20
for epoch in range(num_epochs):
   # Forward pass
   outputs = model(X_tensor)
   loss = criterion(outputs, X_tensor)

   # Backward pass and optimization
   optimizer.zero_grad()
   loss.backward()
   optimizer.step()

   # Loss for each epoch
   print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

# Encoding the data using the trained autoencoder
encoded_data = model.encoder(X_tensor).detach().numpy()

Epoch [1/20], Loss: 1.2443
Epoch [2/20], Loss: 1.2410
Epoch [3/20], Loss: 1.2376
Epoch [4/20], Loss: 1.2342
Epoch [5/20], Loss: 1.2307
Epoch [6/20], Loss: 1.2271
Epoch [7/20], Loss: 1.2234
Epoch [8/20], Loss: 1.2196
Epoch [9/20], Loss: 1.2156
Epoch [10/20], Loss: 1.2114
Epoch [11/20], Loss: 1.2070
Epoch [12/20], Loss: 1.2023
Epoch [13/20], Loss: 1.1974
Epoch [14/20], Loss: 1.1923
Epoch [15/20], Loss: 1.1868
Epoch [16/20], Loss: 1.1811
Epoch [17/20], Loss: 1.1751
Epoch [18/20], Loss: 1.1688
Epoch [19/20], Loss: 1.1622
Epoch [20/20], Loss: 1.1554

Por último, ahora podemos trazar las dimensiones de incrustación resultantes (Figura 4). Como puede verse en la imagen de abajo, conseguimos reducir la dimensionalidad de nuestro conjunto de características de 17 dimensiones a sólo 3, sin dejar de ser capaces, en buena medida, de separar correctamente en nuestro espacio tridimensional las muestras entre las distintas clases.

# Plotting the encoded data in 3D space
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
scatter = ax.scatter(encoded_data[:, 0], encoded_data[:, 1],
                    encoded_data[:, 2], c=Y_numerical, cmap='viridis')

# Mapping numerical labels back to original string labels for the legend
labels = label_encoder.inverse_transform(np.unique(Y_numerical))
legend_labels = {num: label for num, label in zip(np.unique(Y_numerical),
                                                 labels)}

# Creating a custom legend with original string labels
handles = [plt.Line2D([0], [0], marker='o', color='w',
                    markerfacecolor=scatter.to_rgba(num),
                    markersize=10,
                    label=legend_labels[num]) for num in np.unique(Y_numerical)]
ax.legend(handles=handles, title="Raining Tomorrow?")

# Adjusting the layout to provide more space for labels
ax.xaxis.labelpad = 20
ax.yaxis.labelpad = 20

ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])

# Manually adding z-axis label for better visibility
ax.text2D(0.05, 0.95, 'Encoded Dimension 3', transform=ax.transAxes,
         fontsize=12, color='black')

ax.set_xlabel('Encoded Dimension 1')
ax.set_ylabel('Encoded Dimension 2')
ax.set_title('Autoencoder Dimensionality Reduction')

plt.tight_layout()

plt.savefig('Rain_Prediction_Autoencoder.png')

plt.show()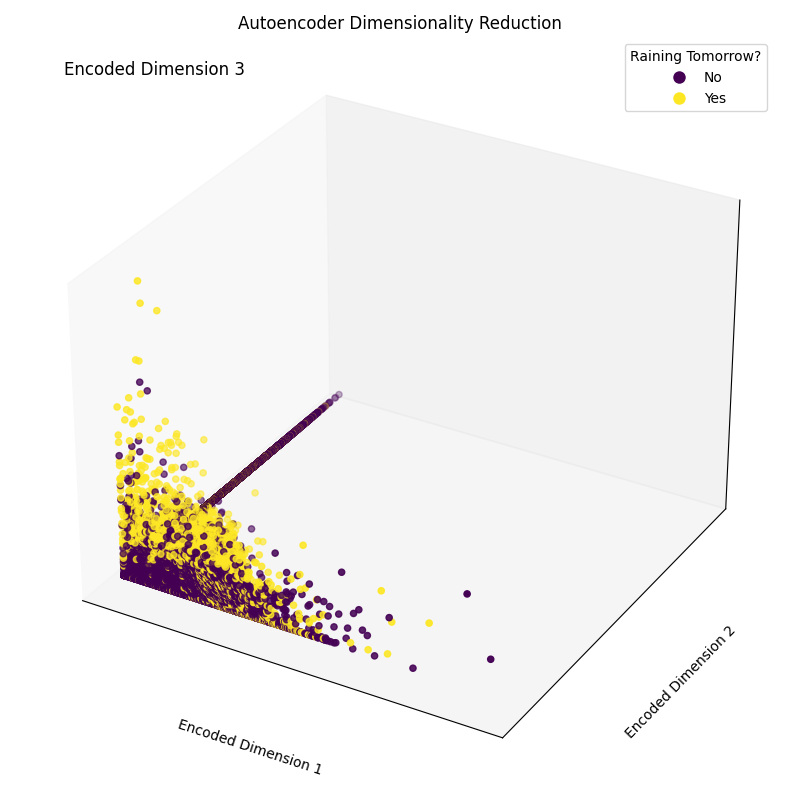

Figura 4: Dimensiones codificadas resultantes (Imagen del autor).

Aplicaciones reales de los autocodificadores

Compresión/Denotación de imágenes

Una de las principales aplicaciones de los Autocodificadores es comprimir imágenes para reducir su tamaño total de archivo, intentando conservar al mismo tiempo la mayor cantidad posible de información valiosa, o restaurar imágenes que se han degradado con el tiempo.

Detección de anomalías

Como los autocodificadores son buenos para distinguir las características esenciales de los datos del ruido, pueden utilizarse para detectar anomalías (por ejemplo, si una imagen ha sido retocada con Photoshop, si hay actividades inusuales en una red, etc.).

Generación de datos

Los Autocodificadores Variacionales y las Redes Generativas Adversariales (GAN) se utilizan con frecuencia para generar datos sintéticos (por ejemplo, imágenes realistas de personas).

Conclusión

En conclusión, los Autocodificadores pueden ser una herramienta realmente flexible para potenciar diferentes formas de casos de uso. En particular, los Autocodificadores Variacionales y la creación de las GAN abrieron la puerta al desarrollo de la IA Generativa, ofreciéndonos los primeros atisbos de cómo se puede utilizar la IA para generar nuevas formas de contenido nunca vistas.

Este tutorial ha sido una introducción al campo de los Autocodificadores, ¡aunque todavía queda mucho por aprender! DataCamp tiene una gran variedad de recursos sobre este tema, como por ejemplo, ¡cómo implementar Autoencoders en Keras o utilizarlos como clasificadores!