Introduction aux autoencodeurs : Des bases aux applications avancées de PyTorch

Les réseaux neuronaux feedforward traditionnels peuvent être très efficaces pour effectuer des tâches telles que la classification et la régression, mais qu'en est-il si nous souhaitons mettre en œuvre des solutions telles que le débruitage de signaux ou la détection d'anomalies ? L'une des façons d'y parvenir est d'utiliser des autoencodeurs.

Ce tutoriel fournit une introduction pratique aux autoencodeurs, y compris un exemple pratique dans PyTorch et quelques cas d'utilisation potentiels.

Vous pouvez suivre l'évolution dans ce classeur DataLab avec tout le code du didacticiel.

Qu'est-ce qu'un auto-codeur ?

Les autoencodeurs sont un type particulier de réseau neuronal non supervisé (aucune étiquette n'est nécessaire !). La principale application des autoencodeurs consiste à capturer avec précision les aspects clés des données fournies afin de fournir une version compressée des données d'entrée, de générer des données synthétiques réalistes ou de signaler les anomalies.

Les autoencodeurs sont composés de deux réseaux neuronaux clés entièrement connectés (figure 1) :

• Encodeur: il comprime les données d'entrée pour éliminer toute forme de bruit et génère un espace latent/un goulot d'étranglement. Par conséquent, les dimensions du réseau neuronal de sortie sont inférieures à celles de l'entrée et peuvent être ajustées en tant qu'hyperparamètre afin de décider du niveau de perte de notre compression.
• Décodeur: en utilisant uniquement la représentation comprimée des données de l'espace latent, il tente de reconstruire avec le plus de fidélité possible les données d'entrée originales (l'architecture de ce réseau neuronal est donc généralement une image miroir de celle du codeur). La "qualité" de la prédiction peut alors être mesurée en calculant l'erreur de reconstruction entre les données d'entrée et de sortie à l'aide d'une fonction de perte.

En répétant itérativement ce processus de passage des données à travers le codeur et le décodeur et en mesurant l'erreur pour ajuster les paramètres par rétropropagation, l'auto-codeur peut, avec le temps, travailler correctement avec des formes de données extrêmement difficiles.

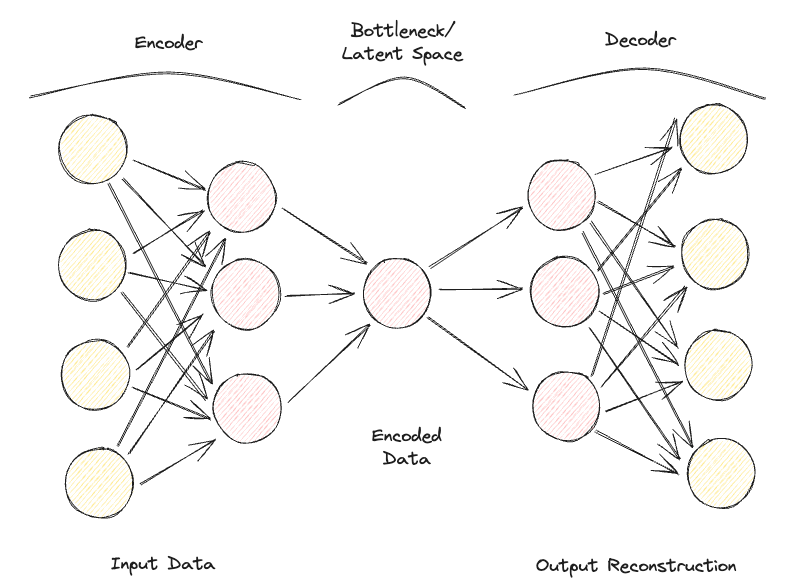
Figure 1 : Architecture de l'autoencodeur (Image de l'auteur).

Si un autoencodeur reçoit un ensemble de caractéristiques d'entrée totalement indépendantes les unes des autres, il sera très difficile pour le modèle de trouver une bonne représentation en dimensions inférieures sans perdre beaucoup d'informations (compression avec perte).

Les autoencodeurs peuvent donc également être considérés comme une technique de réduction de la dimensionnalité qui, par rapport aux techniques traditionnelles telles que l'analyse en composantes principales (ACP), peut utiliser des transformations non linéaires pour projeter les données dans un espace de moindre dimension. Si vous souhaitez en savoir plus sur les autres techniques d'extraction de caractéristiques, vous trouverez des informations complémentaires dans ce tutoriel sur l'extraction de caractéristiques.

En outre, par rapport aux algorithmes de compression de données standard tels que gzpi, les autoencodeurs ne peuvent pas être utilisés comme des algorithmes de compression à usage général, mais sont conçus pour fonctionner au mieux uniquement sur des données similaires sur lesquelles ils ont été formés.

Voici quelques-uns des hyperparamètres les plus courants qui peuvent être réglés lors de l'optimisation de votre autoencodeur :

• Le nombre de couches pour les réseaux neuronaux Encoder et Decoder
• Le nombre de nœuds pour chacune de ces couches
• La fonction de perte à utiliser pour le processus d'optimisation (par exemple, l'entropie croisée binaire ou l'erreur quadratique moyenne).
• La taille de l'espace latent (plus il est petit, plus la compression est élevée, agissant ainsi comme un mécanisme de régularisation).

Enfin, les autoencodeurs peuvent être conçus pour travailler avec différents types de données, telles que des données tabulaires, des séries temporelles ou des données d'image, et peuvent donc être conçus pour utiliser une variété de couches, telles que des couches convolutives, pour l'analyse d'images.

Idéalement, un autoencodeur bien entraîné doit être suffisamment réactif pour s'adapter aux données d'entrée afin de fournir une réponse sur mesure, mais pas trop pour ne faire qu'imiter les données d'entrée et ne pas être en mesure de généraliser avec des données inédites (donc surajustement).

Types d'auto-codeurs

Au fil des ans, différents types d'autoencodeurs ont été développés :

• Autoencodeur incomplet
• Autoencodeur clairsemé
• Autoencodeur contractuel
• Débruitage Autoencodeur
• Autoencodeur convolutif
• Autoencodeur variationnel

Examinons chacun d'entre eux plus en détail.

Autoencodeur incomplet

Il s'agit de la version la plus simple d'un autoencodeur. Dans ce cas, nous n'avons pas de mécanisme de régularisation explicite, mais nous nous assurons que la taille du goulot d'étranglement est toujours inférieure à la taille de l'entrée originale afin d'éviter un surajustement. Ce type de configuration est généralement utilisé comme technique de réduction de la dimensionnalité (plus puissante que l'ACP car elle est également capable de capturer les non-linéarités dans les données).

Autoencodeur clairsemé

Un autoencodeur clairsemé est assez similaire à un autoencodeur sous-complet, mais leur principale différence réside dans la manière dont la régularisation est appliquée. En fait, avec les autoencodeurs épars, nous ne devons pas nécessairement réduire les dimensions du goulot d'étranglement, mais nous utilisons une fonction de perte qui tente de pénaliser le modèle en l'empêchant d'utiliser tous ses neurones dans les différentes couches cachées (figure 2).

Cette pénalité est communément appelée fonction de sparsité, et elle est assez différente des techniques de régularisation traditionnelles puisqu'elle ne pénalise pas la taille des poids mais le nombre de nœuds activés.

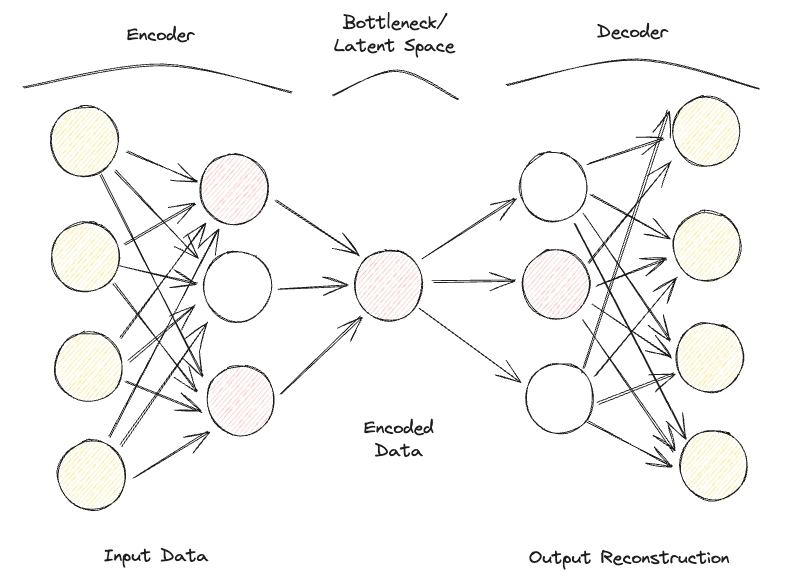
Ainsi, différents nœuds pourraient être spécialisés pour différents types d'entrées et être activés/désactivés en fonction des spécificités des données d'entrée. Cette contrainte de rareté peut être induite par l'utilisation de la régularisation L1 et de la divergence KL, ce qui empêche efficacement le modèle d'être surajouté.

Autoencodeur contractuel

L'idée principale des autoencodeurs contractuels est qu'étant donné des entrées similaires, leur représentation comprimée devrait être assez similaire (les voisinages des entrées devraient être contractés dans un petit voisinage des sorties). En termes mathématiques, ce principe peut être appliqué en maintenant les activations de la couche cachée de l'entrée à un niveau faible lorsqu'elle est alimentée par des entrées similaires.

Débruitage Autoencodeur

Avec les autoencodeurs de débruitage, l'entrée et la sortie du modèle ne sont plus les mêmes. Par exemple, le modèle pourrait être alimenté par des images corrompues à faible résolution et travailler en sortie pour améliorer la qualité des images. Afin d'évaluer les performances du modèle et de l'améliorer au fil du temps, nous devrions disposer d'une certaine forme d'image propre étiquetée à comparer avec la prédiction du modèle.

Autoencodeur convolutif

Pour travailler avec des données d'image, les autoencodeurs convolutifs remplacent les réseaux neuronaux feedforward traditionnels par des réseaux neuronaux convolutifs pour les étapes d'encodage et de décodage. En mettant à jour le type de fonction de perte, etc., ce type d'autoencodeur peut également être conçu, par exemple, comme un autoencodeur clairsemé ou débruiteur, en fonction des exigences de votre cas d'utilisation.

Autoencodeur variationnel

Dans tous les types d'autoencodeurs étudiés jusqu'à présent, le codeur produit une seule valeur pour chaque dimension concernée. Avec les autoencodeurs variationnels (VAE), nous rendons ce processus plutôt probabiliste, en créant une distribution de probabilité pour chaque dimension. Le décodeur peut alors échantillonner une valeur de chaque distribution décrivant les différentes dimensions et construire le vecteur d'entrée, qui peut ensuite être utilisé pour reconstruire les données d'entrée originales.

L'une des principales applications des autoencodeurs variationnels concerne les tâches génératives. En fait, l'échantillonnage du modèle latent à partir de distributions peut permettre au décodeur de créer de nouvelles formes de sorties qui n'étaient pas possibles auparavant avec une approche déterministe.

Si vous souhaitez tester en ligne un autoencodeur variationnel entraîné sur l'ensemble de données MNIST, vous pouvez trouver un exemple en direct.

Exemple pratique d'autoencodeur

Nous sommes maintenant prêts à faire une démonstration pratique de la façon dont les autoencodeurs peuvent être utilisés pour la réduction de la dimensionnalité. Pour cet exercice, nous avons choisi PyTorch comme cadre d'apprentissage profond.

L' ensemble de données Kaggle Rain in Australia sera utilisé pour cette démonstration. Tout le code de cet article est disponible dans ce classeur DataLab.

Tout d'abord, nous importons toutes les bibliothèques nécessaires et supprimons les valeurs manquantes et les colonnes non numériques (figure 3).

import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, LabelEncoder
from mpl_toolkits.mplot3d import Axes3D

df = pd.read_csv("../input/weather-dataset-rattle-package/weatherAUS.csv")
df = df.drop(['Date', 'Location', 'WindDir9am',
             'WindGustDir', 'WindDir3pm'], axis=1)
df = df.dropna(how = 'any')
df.loc[df['RainToday'] == 'No', 'RainToday'] = 0
df.loc[df['RainToday'] == 'Yes', 'RainToday'] = 1
df.head()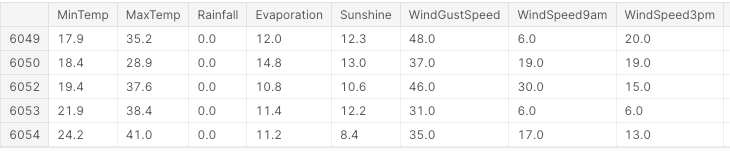

Figure 3 : Exemple de colonnes d'un ensemble de données (Image de l'auteur).

À ce stade, nous sommes prêts à diviser les données en caractéristiques et en étiquettes, à normaliser les caractéristiques et à convertir les étiquettes en format numérique.

Dans ce cas, nous disposons d'un ensemble de caractéristiques de départ composé de 17 colonnes. L'objectif global de l'analyse serait alors de prédire correctement s'il va pleuvoir le lendemain ou non.

X, Y = df.drop('RainTomorrow', axis=1, inplace=False), df[['RainTomorrow']]
# Normalizing Data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Converting to PyTorch tensor
X_tensor = torch.FloatTensor(X_scaled)

# Converting string labels to numerical labels
label_encoder = LabelEncoder()
Y_numerical = label_encoder.fit_transform(Y.values.ravel())

Dans PyTorch, nous pouvons maintenant définir le modèle Autoencoder comme une classe et spécifier les modèles d'encodage et de décodage avec deux couches linéaires.

# Defining Autoencoder model
class Autoencoder(nn.Module):
   def __init__(self, input_size, encoding_dim):
       super(Autoencoder, self).__init__()
       self.encoder = nn.Sequential(
           nn.Linear(input_size, 16),
           nn.ReLU(),
           nn.Linear(16, encoding_dim),
           nn.ReLU()
       )
       self.decoder = nn.Sequential(
           nn.Linear(encoding_dim, 16),
           nn.ReLU(),
           nn.Linear(16, input_size),
           nn.Sigmoid()
       )

   def forward(self, x):
       x = self.encoder(x)
       x = self.decoder(x)
       return x

Maintenant que le modèle est établi, nous pouvons spécifier que nos dimensions d'encodage sont égales à 3 (pour faciliter le tracé ultérieur) et lancer le processus d'apprentissage.

# Setting random seed for reproducibility
torch.manual_seed(42)

input_size = X.shape[1]  # Number of input features
encoding_dim = 3  # Desired number of output dimensions
model = Autoencoder(input_size, encoding_dim)

# Loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)

# Training the autoencoder
num_epochs = 20
for epoch in range(num_epochs):
   # Forward pass
   outputs = model(X_tensor)
   loss = criterion(outputs, X_tensor)

   # Backward pass and optimization
   optimizer.zero_grad()
   loss.backward()
   optimizer.step()

   # Loss for each epoch
   print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

# Encoding the data using the trained autoencoder
encoded_data = model.encoder(X_tensor).detach().numpy()

Epoch [1/20], Loss: 1.2443
Epoch [2/20], Loss: 1.2410
Epoch [3/20], Loss: 1.2376
Epoch [4/20], Loss: 1.2342
Epoch [5/20], Loss: 1.2307
Epoch [6/20], Loss: 1.2271
Epoch [7/20], Loss: 1.2234
Epoch [8/20], Loss: 1.2196
Epoch [9/20], Loss: 1.2156
Epoch [10/20], Loss: 1.2114
Epoch [11/20], Loss: 1.2070
Epoch [12/20], Loss: 1.2023
Epoch [13/20], Loss: 1.1974
Epoch [14/20], Loss: 1.1923
Epoch [15/20], Loss: 1.1868
Epoch [16/20], Loss: 1.1811
Epoch [17/20], Loss: 1.1751
Epoch [18/20], Loss: 1.1688
Epoch [19/20], Loss: 1.1622
Epoch [20/20], Loss: 1.1554

Enfin, nous pouvons maintenant tracer les dimensions d'encastrement obtenues (figure 4). Comme le montre l'image ci-dessous, nous avons réussi à réduire la dimensionnalité de notre ensemble de caractéristiques de 17 dimensions à seulement 3, tout en étant capables, dans une large mesure, de séparer correctement les échantillons des différentes classes dans notre espace tridimensionnel.

# Plotting the encoded data in 3D space
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
scatter = ax.scatter(encoded_data[:, 0], encoded_data[:, 1],
                    encoded_data[:, 2], c=Y_numerical, cmap='viridis')

# Mapping numerical labels back to original string labels for the legend
labels = label_encoder.inverse_transform(np.unique(Y_numerical))
legend_labels = {num: label for num, label in zip(np.unique(Y_numerical),
                                                 labels)}

# Creating a custom legend with original string labels
handles = [plt.Line2D([0], [0], marker='o', color='w',
                    markerfacecolor=scatter.to_rgba(num),
                    markersize=10,
                    label=legend_labels[num]) for num in np.unique(Y_numerical)]
ax.legend(handles=handles, title="Raining Tomorrow?")

# Adjusting the layout to provide more space for labels
ax.xaxis.labelpad = 20
ax.yaxis.labelpad = 20

ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])

# Manually adding z-axis label for better visibility
ax.text2D(0.05, 0.95, 'Encoded Dimension 3', transform=ax.transAxes,
         fontsize=12, color='black')

ax.set_xlabel('Encoded Dimension 1')
ax.set_ylabel('Encoded Dimension 2')
ax.set_title('Autoencoder Dimensionality Reduction')

plt.tight_layout()

plt.savefig('Rain_Prediction_Autoencoder.png')

plt.show()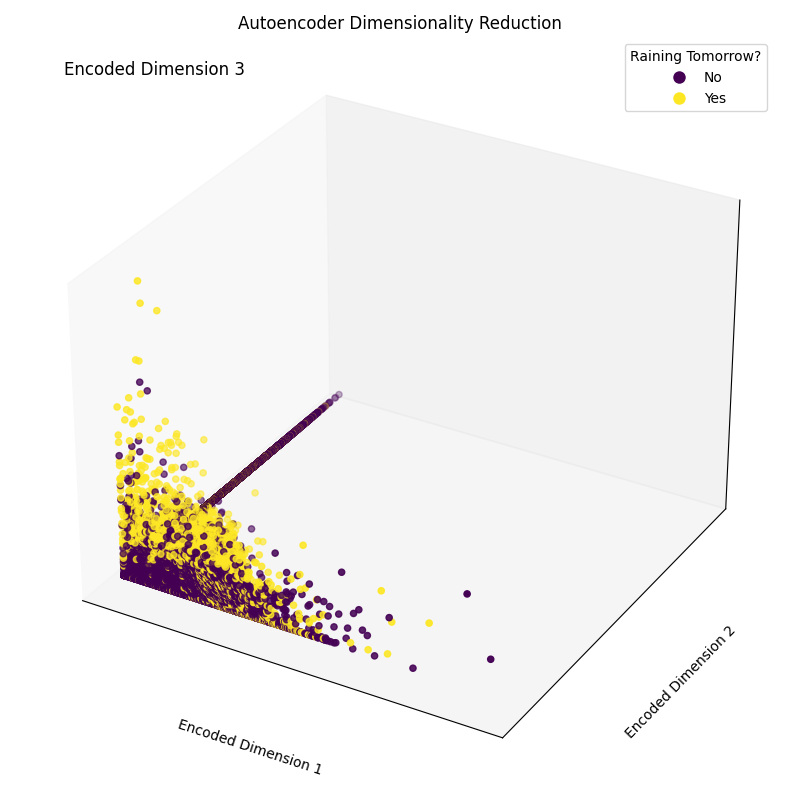

Figure 4 : Dimensions codées résultantes (image de l'auteur).

Applications réelles des autoencodeurs

Compression d'image/dénoisage

L'une des principales applications des autoencodeurs consiste à compresser les images afin de réduire leur taille globale tout en essayant de conserver autant d'informations précieuses que possible ou de restaurer des images qui ont été dégradées au fil du temps.

Détection des anomalies

Les autoencodeurs étant capables de distinguer les caractéristiques essentielles des données du bruit, ils peuvent être utilisés pour détecter des anomalies (par exemple, si une image a été retouchée, s'il y a des activités inhabituelles dans un réseau, etc.)

Génération de données

Les autoencodeurs variationnels et les réseaux adversariaux génératifs (GAN) sont fréquemment utilisés pour générer des données synthétiques (par exemple, des images réalistes de personnes).

Conclusion

En conclusion, les autoencodeurs peuvent être un outil très flexible pour alimenter différentes formes de cas d'utilisation. En particulier, les autoencodeurs variationnels et la création des GAN ont ouvert la voie au développement de l'IA générative, nous donnant un premier aperçu de la manière dont l'IA peut être utilisée pour générer de nouvelles formes de contenu jamais vues auparavant.

Ce tutoriel était une introduction au domaine des Autoencodeurs, bien qu'il y ait encore beaucoup à apprendre ! DataCamp dispose d'une grande variété de ressources sur ce sujet, comme par exemple comment mettre en œuvre des Autoencodeurs dans Keras ou les utiliser comme classificateur!