Imagina que estás entrenando un modelo de aprendizaje automático, pero no estás seguro de cómo se comportará con datos nuevos y desconocidos. Ahí es donde entra en juego la validación cruzada K-Fold. Ofrece un anticipo de cómo le iría a tu modelo en el mundo real. Esta técnica te ayuda a asegurarte de que tus predicciones no son sólo una maravilla de un solo acierto, sino que son fiables de forma consistente en nuevos conjuntos de datos nunca vistos.
En esta guía, desentrañaremos los fundamentos de la validación cruzada K-Fold y la compararemos con métodos más sencillos como la división entrenamiento-prueba. Explorarás varios métodos de validación cruzada utilizando Python y comprenderás por qué elegir el adecuado puede tener un gran impacto en tus proyectos. Al final, estarás equipado para aplicar estas estrategias con scikit-Learn.
Sumerjámonos y aprendamos a hacer que tus esfuerzos de aprendizaje automático sean realmente fiables.
¿Qué es la validación cruzada K-Fold?
La validación cruzada K-Fold es una técnica robusta que se utiliza para evaluar el rendimiento de los modelos de aprendizaje automático. Ayuda a garantizar que el modelo generaliza bien a los datos no vistos, utilizando diferentes porciones del conjunto de datos para el entrenamiento y la prueba en múltiples iteraciones.
Validación cruzada K-Fold frente a Dividir entrenamiento-prueba
Mientras que la validación cruzada K-Fold divide el conjunto de datos en varios subconjuntos para entrenar y probar iterativamente el modelo, el método de división entrenar-prueba divide el conjunto de datos en sólo dos partes: una para entrenar y otra para probar. El método de división entrenamiento-prueba es sencillo y rápido de aplicar, pero la estimación del rendimiento puede depender mucho de la división concreta, lo que provoca una gran variación en los resultados.
Las imágenes siguientes ilustran las diferencias estructurales entre estos dos métodos. La primera imagen muestra el método de división entrenamiento-prueba, en el que el conjunto de datos se divide en un 80% de segmentos de entrenamiento y un 20% de segmentos de prueba.
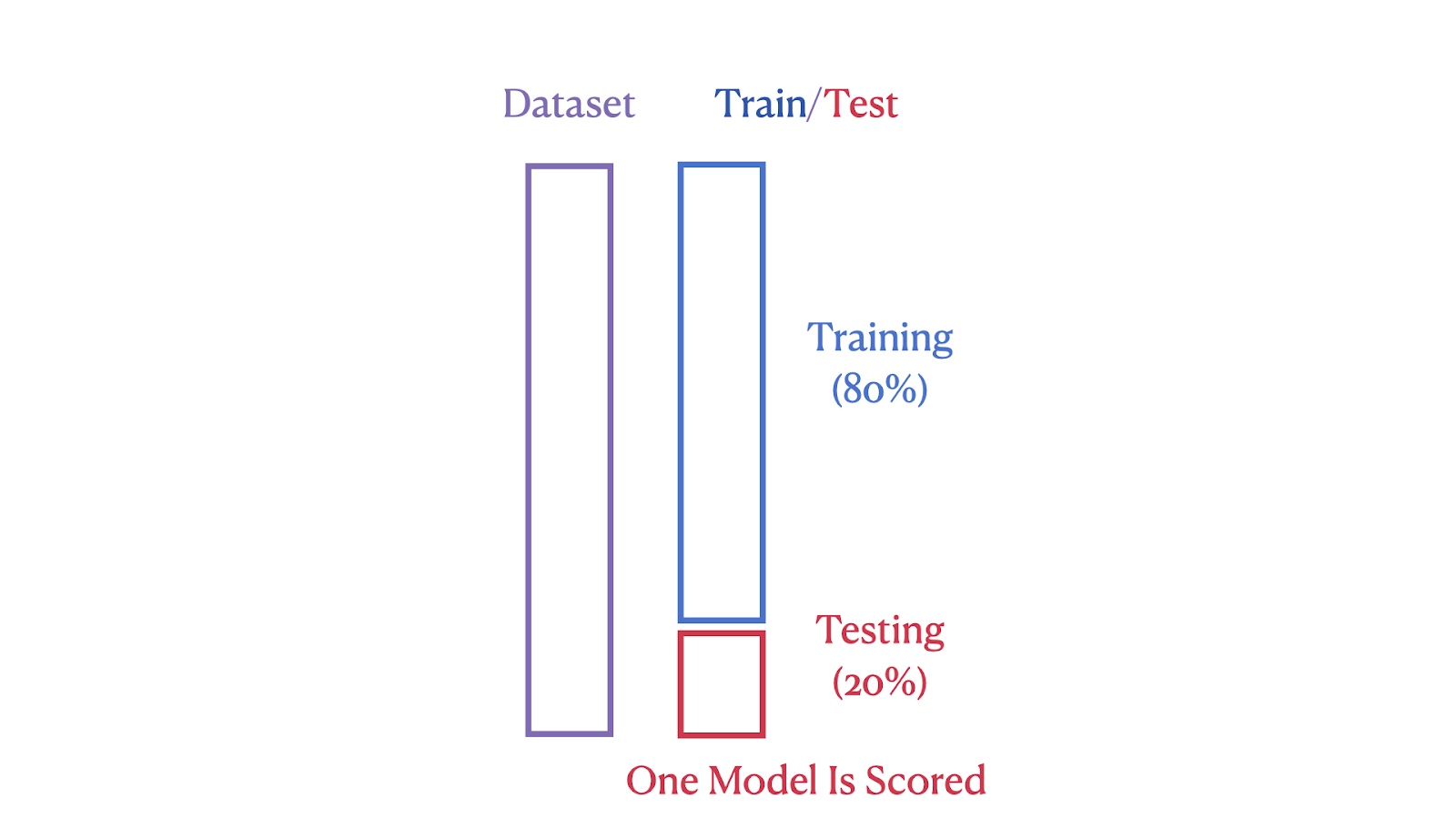
Ilustración de la división entrenamiento/prueba. Imagen del autor
La segunda imagen muestra una validación cruzada quíntuple, en la que el conjunto de datos se divide en cinco partes, y cada parte sirve como conjunto de prueba en una de las cinco iteraciones, asegurando que cada segmento se utiliza tanto para el entrenamiento como para la prueba.
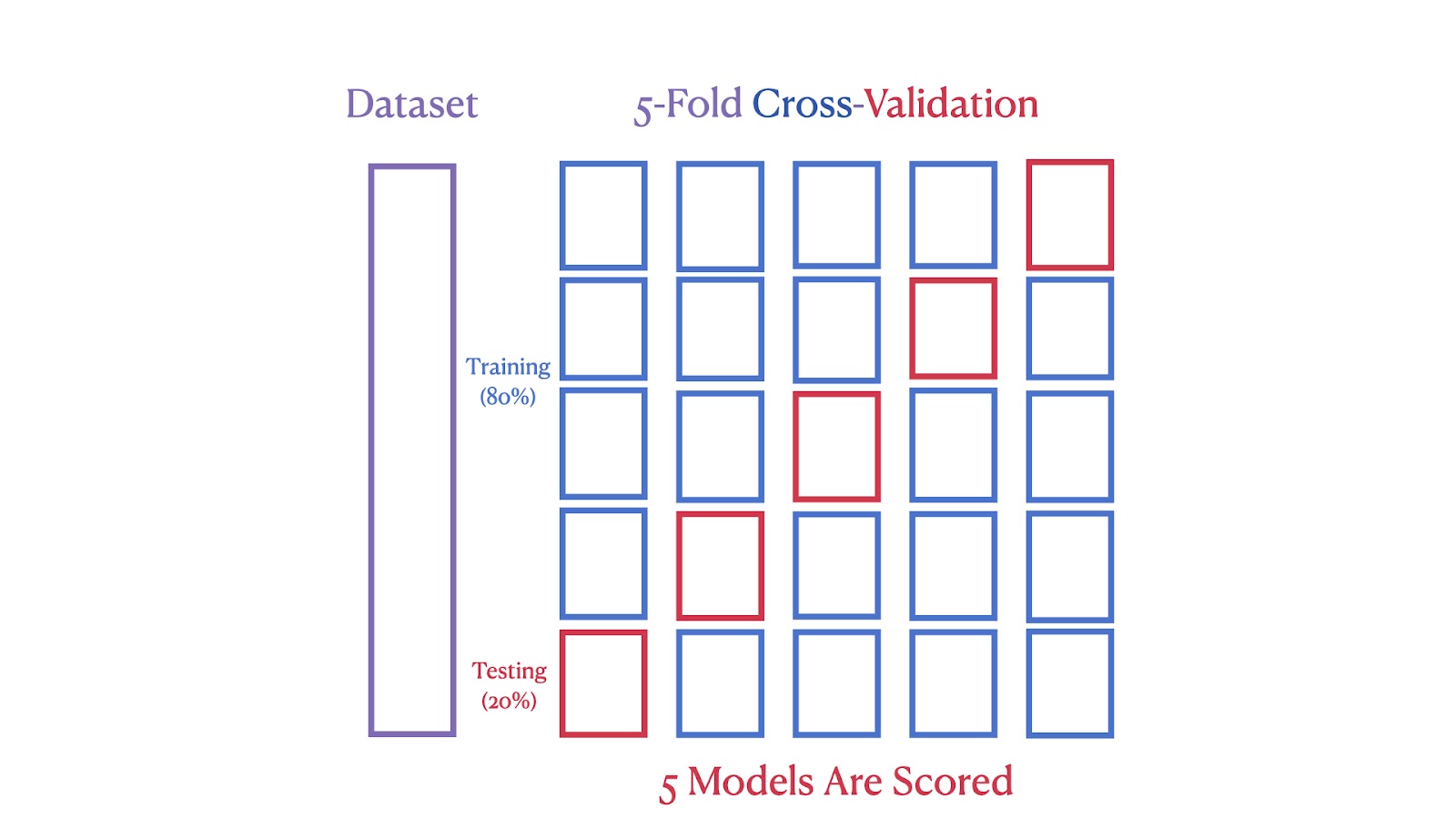
Esquema de validación cruzada quíntuple. Imagen del autor
Podemos ver que la validación cruzada K-Fold proporciona una estimación del rendimiento más sólida y fiable, porque reduce el impacto de la variabilidad de los datos. Al utilizar varios ciclos de entrenamiento y prueba, minimiza el riesgo de sobreajuste a una determinada división de datos. Este método también garantiza que cada punto de datos se utilice tanto para el entrenamiento como para la validación, lo que da lugar a una evaluación más completa del rendimiento del modelo.
Implementación de la validación cruzada K-Fold en Python con scikit-learn
Vamos a demostrar ahora la Validación Cruzada K-Fold utilizando el conjunto de datos de Viviendas de California para evaluar el rendimiento de un modelo de regresión lineal. Este método proporciona una estimación robusta de la precisión del modelo mediante pruebas iterativas en diferentes subconjuntos del conjunto de datos, lo que garantiza una evaluación exhaustiva.
Visión general del conjunto de datos de Viviendas de California
El Conjunto de Datos de Vivienda de California, recopilado por Pace y Barry (1997), contiene datos de la Encuesta Nacional de 1990. Censo sobre la vivienda en California. Incluye 20.640 observaciones con características como ubicación, antigüedad de la vivienda y población. La variable objetivo es el valor medio de la vivienda en los distritos de California.
El conjunto de datos proporciona un conjunto diverso de características geográficas, demográficas y económicas, lo que lo hace muy adecuado para aplicaciones de ciencia de datos y aprendizaje automático. Comenzaremos nuestro ejemplo de codificación descargándolo directamente de la biblioteca scikit-Learn.
Cargar el conjunto de datos
Antes de empezar con el entrenamiento y la evaluación del modelo, tenemos que cargar el conjunto de datos.
from sklearn.datasets import fetch_california_housing
data = fetch_california_housing()Este código importa la función fetch_california_housing de sklearn.datasets y luego la llama para cargar el conjunto de datos de Viviendas de California. Este conjunto de datos se almacena en los datos variables, que contienen tanto las características como la variable objetivo.
Preparación de los datos
Una vez cargado el conjunto de datos, el siguiente paso es preparar los datos para el análisis.
import pandas as pd
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.targetAquí, utilizamos la biblioteca pandas para crear un DataFrame X que contenga los datos de las características de data.data. Las columnas del DataFrame se etiquetan utilizando data.feature_names. La variable objetivo, que representa los valores medios de las viviendas, se almacena por separado en y.
Configuración de la validación cruzada K-Fold
Ahora es el momento de configurar nuestro modelo, incluida la selección de un valor para K. Elegir el valor correcto para K es un paso importante que trataremos en detalle más adelante.
from sklearn.model_selection import KFold
k = 5
kf = KFold(n_splits=k, shuffle=True, random_state=42)Este código inicializa la validación cruzada K-Fold utilizando la clase KFold de sklearn.model_selection. Configuramos la instancia kf con 5 divisiones. La opción shuffle=True aleatoriza el orden de los puntos de datos, y random_state=42 garantiza que este barajado sea coherente en varias ejecuciones. Esta configuración suele ser suficiente para empezar a evaluar el rendimiento de un modelo con validación cruzada.
Inicializar el modelo
Con nuestros datos preparados y la validación cruzada establecida, el siguiente paso es elegir e inicializar el modelo.
from sklearn.linear_model import LinearRegression
model = LinearRegression()Importamos la clase LinearRegression de sklearn.linear_model y creamos un modelo de instancia. Este modelo se utilizará para realizar una regresión lineal sobre el conjunto de datos.
Realizar la validación cruzada
Ahora que el modelo está inicializado, podemos pasar a la parte divertida y realizar una validación cruzada para evaluar su rendimiento en diferentes subconjuntos de datos.
from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X, y, cv=kf, scoring='r2')Esta línea utiliza la función cross_val_score para evaluar el modelo utilizando el conjunto de datos X y el objetivo y. La validación cruzada se realiza utilizando la instancia Kfold kf , y el rendimiento del modelo se mide utilizando la puntuación R².
Cálculo de la puntuación media R2
Podemos utilizar la R-cuadrado como métrica para evaluar la proporción de varianza de la variable dependiente que es predecible a partir de las variables independientes, lo que proporciona una idea de la bondad del ajuste del modelo de regresión.
import numpy as np
average_r2 = np.mean(scores)
print(f"R² Score for each fold: {[round(score, 4) for score in scores]}")
print(f"Average R² across {k} folds: {average_r2:.2f}")Esta parte calcula la puntuación R² media de todos los pliegues. Las puntuaciones de cada pliegue se imprimen primero, seguidas de la puntuación media. El uso de np.mean() calcula la media de las puntuaciones recogidas durante la validación cruzada.
Mostrar los resultados finales
Ahora agregamos los resultados para obtener una comprensión global del rendimiento del modelo. La puntuación media de R² proporciona una única métrica que indica la eficacia del modelo.
R² Score for each fold: [0.5758, 0.6137, 0.6086, 0.6213, 0.5875]
Average R² across 5 folds: 0.60Este es el resultado del código del paso anterior. Muestra las puntuaciones R² de cada pliegue y la puntuación R² media.
¿Qué representa "K" en la validación cruzada K-Fold?
En la validación cruzada de K pliegues, "K" representa el número de grupos en que se divide el conjunto de datos. Este número determina cuántas rondas de pruebas se someten al modelo, asegurándose de que cada segmento se utiliza como conjunto de pruebas una vez.
He aquí una heurística:
- K = 2 ó 3: Estas opciones pueden ser beneficiosas cuando los recursos computacionales son limitados o cuando se necesita una evaluación más rápida. Reducen el número de ciclos de entrenamiento, con lo que ahorran tiempo y potencia de cálculo, al tiempo que proporcionan una estimación razonable del rendimiento del modelo.
- K = 5 ó 10: Elegir K = 5 o K = 10 son opciones populares porque proporcionan un buen equilibrio entre la eficiencia computacional y la estimación del rendimiento del modelo.
- K = 20: Utilizar un valor mayor de K puede proporcionar una evaluación más detallada del rendimiento. Sin embargo, aumenta la carga computacional y puede dar lugar a una mayor varianza si los subconjuntos son demasiado pequeños.
Para saber más sobre la estimación del rendimiento de los modelos, considera la posibilidad de seguir nuestro curso completo Validación de Modelos en Python.
Consideraciones clave al utilizar la validación cruzada K-Fold
El impacto de "K" en la validación cruzada K-Fold
El número de pliegues, o "K", en la validación cruzada de pliegues K afecta tanto a la granularidad del proceso de validación como a la carga computacional. Una K más pequeña (por ejemplo, 3-5) podría ser más rápida, pero podría dar lugar a estimaciones menos fiables, ya que cada pliegue representa una porción mayor del conjunto de datos, con lo que podrían perderse diversos escenarios de datos. Una K mayor (por ejemplo, 10) proporciona una evaluación más detallada a costa de un mayor cálculo. Un punto de partida habitual es K=5 o K=10, que suelen ser suficientes para obtener una estimación fiable sin cálculos excesivos.
Importancia de barajar los datos en la validación cruzada K-Fold
Barajar los datos en la Validación Cruzada K-Fold es muy recomendable para mejorar la validez de la evaluación del modelo. Al establecer barajar=Verdadero, la barajación rompe cualquier orden inherente al conjunto de datos que pudiera introducir sesgos durante el proceso de validación. Esto garantiza que cada pliegue sea representativo de todo el conjunto de datos, lo que es crucial para evaluar lo bien que generaliza el modelo a los nuevos datos. Sin embargo, es importante evitar el barajado en los casos en que la secuencia de puntos de datos sea significativa, como ocurre con los datos de series temporales, para preservar la integridad del proceso de aprendizaje.
Garantizar la reproducibilidad en la validación cruzada K-Fold
Garantizar que los resultados de la validación cruzada K-Fold sean reproducibles es crucial para verificar la estabilidad y el rendimiento del modelo. Esto se puede conseguir configurando el parámetro estado_aleatorio, que garantiza un barajado coherente de los datos en diferentes ejecuciones, lo que permite obtener divisiones de datos idénticas y, por tanto, resultados reproducibles.
Pliegue K estándar frente a Otros métodos de validación cruzada
Elegir la técnica de validación cruzada adecuada es crucial para construir modelos de aprendizaje automático fiables. La elección depende en gran medida de las características específicas del conjunto de datos y del tipo de tarea de aprendizaje automático de que se trate. Se han diseñado diferentes técnicas para hacer frente a diversos retos, como los datos desequilibrados o las estructuras de datos agrupados.
La tabla siguiente ofrece una comparación exhaustiva de los distintos métodos de validación cruzada más populares, destacando sus características únicas y los mejores casos de uso para guiarte en la selección de la técnica más eficaz para tus necesidades específicas de modelado.
| Tipo de CV | Utilización | Descripción | Cuándo utilizar |
|---|---|---|---|
| Validación cruzada K-fold estándar | Tanto la regresión como la clasificación | Divide el conjunto de datos en k pliegues de igual tamaño. Cada pliegue se utiliza una vez como conjunto de prueba. | Mejor para conjuntos de datos equilibrados que garanticen una evaluación completa del modelo. |
| Validación cruzada K-fold estratificada | Principalmente clasificación | Mantiene la misma proporción de etiquetas de clase en cada pliegue que el conjunto de datos original. | Ideal para tareas de clasificación con clases desequilibradas para mantener las proporciones de los grupos. |
| Validación cruzada sin exclusión (LOOCV) | Tanto la regresión como la clasificación | Cada punto de datos se utiliza una vez como conjunto de prueba, y el resto como entrenamiento. | Genial para conjuntos de datos pequeños para maximizar los datos de entrenamiento, aunque computacionalmente intensivo. |
| Validación cruzada Leave-P-Out | Tanto la regresión como la clasificación | Similar a LOOCV, pero omite p puntos de datos del conjunto de prueba. | Ideal para conjuntos de datos pequeños, para comprobar cómo afectan los cambios en las muestras de datos a la estabilidad del modelo. |
| Grupo K-Validación cruzada | Tanto la regresión como la clasificación con grupos | Garantiza que ningún grupo esté tanto en el conjunto de entrenamiento como en el de prueba, lo que es útil cuando los puntos de datos no son independientes. | Ideal para conjuntos de datos con agrupaciones lógicas para comprobar el rendimiento en grupos independientes. |
| Grupo estratificado Validación cruzada K-Fold | Principalmente clasificación con datos agrupados | Combina la estratificación y la integridad de grupo, garantizando que los grupos no se dividan entre pliegues. | Ideal para conjuntos de datos agrupados y desequilibrados, para mantener la integridad tanto de las clases como de los grupos. |
Conclusión
Esta guía te ha mostrado cómo la Validación Cruzada K-Fold es una potente herramienta para evaluar modelos de aprendizaje automático. Es mejor que la simple división Entrenar-Probar, porque pone a prueba el modelo en varias partes de tus datos, lo que te ayuda a confiar en que también funcionará bien en datos no vistos.
Si te estás sumergiendo en el aprendizaje automático, aquí tienes algunos recursos que te ayudarán:
- Curso de Aprendizaje Supervisado con Scikit-Learn de DataCamp: Este curso te ayuda a familiarizarte con la modelización predictiva. Es práctico, ideal para iniciar tu viaje. Consulta el curso aquí.
- Tutorial de Aprendizaje Automático con Python: Este tutorial desglosa las ideas clave del aprendizaje automático y te muestra cómo aplicarlas. Es perfecto para solidificar lo que sabes. Lee el tutorial aquí.
- Hoja de trucos de Scikit-Learn: Ten a mano esta hoja de trucos. Es perfecto para recordar rápidamente cómo utilizar las funciones de aprendizaje automático cuando estás trabajando en proyectos. Consigue la hoja de trucos aquí.
- Curso Kaggle Competition de DataCamp: Si quieres poner a prueba tus habilidades, este curso es estupendo. Te enseña a brillar en las competiciones de Kaggle, donde puedes aplicar lo que has aprendido de forma divertida y competitiva. Inicia el curso aquí.
Estos recursos están aquí para guiarte, tanto si estás empezando como si quieres refrescar tus conocimientos. Ofrecen una mezcla de teoría y consejos prácticos, asegurándose de que estás bien preparado para construir y perfeccionar modelos precisos.
Preguntas frecuentes
¿Cómo interpretas las puntuaciones de validación cruzada obtenidas con la validación cruzada K-Fold?
Las puntuaciones de la validación cruzada proporcionan una estimación del rendimiento del modelo en datos no vistos. Una puntuación media más alta en todos los pliegues indica una mejor generalización. Sin embargo, también es importante tener en cuenta la varianza de las puntuaciones entre pliegues. Una varianza elevada sugiere que el rendimiento del modelo es sensible a la división concreta de los datos, lo que puede indicar un ajuste excesivo o la necesidad de más datos. Busca una puntuación media alta con una varianza baja para obtener un modelo sólido y fiable.
¿Puedes utilizar la validación cruzada K-Fold para datos de series temporales?
La validación cruzada K-fold estándar supone que los datos se distribuyen de forma independiente e idéntica, lo que se incumple en las series temporales debido a las dependencias temporales. Para las series temporales, debes utilizar técnicas como la división de series temporales o el encadenamiento hacia delante, en las que el conjunto de entrenamiento sólo incluye puntos de datos ocurridos antes del conjunto de prueba.
¿Cuáles son los errores más comunes que hay que evitar al configurar la validación cruzada K-Fold?
Algunos errores comunes son no barajar los datos, lo que puede introducir un sesgo si el conjunto de datos tiene un orden inherente, e ignorar la aleatoriedad en las asignaciones de pliegues, lo que puede dar lugar a variaciones en el rendimiento del modelo en diferentes ejecuciones. Asegurarse de que se barajan los datos (cuando proceda) y establecer un random_state fijo para la reproducibilidad son prácticas clave para evitar estos problemas.
¿Puede utilizarse la validación cruzada K-Fold para tareas de aprendizaje no supervisado?
Aunque la validación cruzada de pliegues K se utiliza normalmente en el aprendizaje supervisado para estimar el rendimiento predictivo, puede adaptarse a algunas tareas no supervisadas, como la agrupación, mediante la evaluación de la estabilidad de las asignaciones de grupos en los distintos pliegues. Sin embargo, no es tan sencillo como en los entornos supervisados.
¿Cómo gestiona la validación cruzada K-Fold los conjuntos de datos con múltiples escalas de características?
La propia validación cruzada K-Fold no maneja directamente escalas de características múltiples. Es importante preprocesar el conjunto de datos, normalmente mediante normalización o estandarización, antes de aplicar la Validación Cruzada K-Fold. Esto garantiza que los rasgos con escalas mayores no dominen el proceso de aprendizaje del modelo, lo que conduce a una evaluación del modelo más generalizable y justa.
