Programa
Excel Fundamentals
0 min
La desigualdad es un tema que afecta a casi todos los aspectos de la vida: ingresos, riqueza, salud, educación e incluso cómo se distribuyen los recursos en los ecosistemas. Pero, ¿cómo lo medimos realmente? Una de las herramientas más potentes que he encontrado para visualizar la desigualdad es la curva de Lorenz.
Aunque se utiliza habitualmente para medir la desigualdad de ingresos, la curva de Lorenz no es sólo para los economistas. Con el tiempo, se ha convertido en una herramienta versátil utilizada para examinar las disparidades sanitarias, estudiar la biodiversidad e incluso en el aprendizaje automático para evaluar la equidad en los modelos predictivos. Para los científicos de datos, es una forma estupenda de contar una historia sobre la desigualdad en un conjunto de datos.
En este tutorial, te mostraré cómo funciona la curva de Lorenz. Hablaremos de cómo crearlo con tu conjunto de datos, utilizando Python, y aprenderás a utilizarlo en tus propios proyectos. Si te interesa cuantificar la desigualdad de ingresos, analizar la segmentación de los clientes o investigar la asignación de recursos, la curva de Lorenz puede ayudarte a comunicar estas ideas complejas con un sencillo elemento visual.
Comprender la curva de Lorenz
La curva de Lorenz fue introducida en 1905 por el economista Max O. Lorenz. Funciona comparando la distribución real de un recurso con una línea hipotética de igualdad perfecta (una línea en la que todos tienen la misma cantidad). Cuanto más se aleje la curva de esta línea de igualdad perfecta, mayor será la desigualdad en la distribución de ese recurso concreto.
Estructura de la curva de Lorenz
La curva de Lorenz tiene una estructura sencilla. En su eje x, trazamos la proporción acumulativa de la población, empezando por el individuo más pobre y avanzando hasta el más rico. El eje y muestra la parte acumulada del recurso que se está midiendo.
A continuación, tenemos que añadir la línea de igualdad perfecta, que es una línea diagonal que va de la esquina inferior izquierda a la esquina superior derecha. Esta línea representa un escenario en el que todos tienen la misma parte del recurso que nos interesa.
La propia curva de Lorenz muestra la distribución real del recurso. Cuanto más se aleja la curva de la línea de igualdad perfecta, mayor es la desigualdad que representa.
Cómo interpretar la curva de Lorenz
Si la curva de Lorenz está cerca de la línea diagonal de la igualdad perfecta, significa que el recurso está distribuido de forma bastante uniforme. Por ejemplo, en una sociedad en la que el 50% inferior de la población tiene aproximadamente el 50% de los ingresos, la curva de Lorenz estará más cerca de la diagonal. Esta curva poco pronunciada indica una desigualdad baja.
En cambio, si la curva se curva lejos de la diagonal, indica una desigualdad elevada. Esto puede ocurrir si, por ejemplo, el 50% inferior de la población sólo tiene el 10% de los ingresos, mientras que el 10% superior tiene todo el resto.
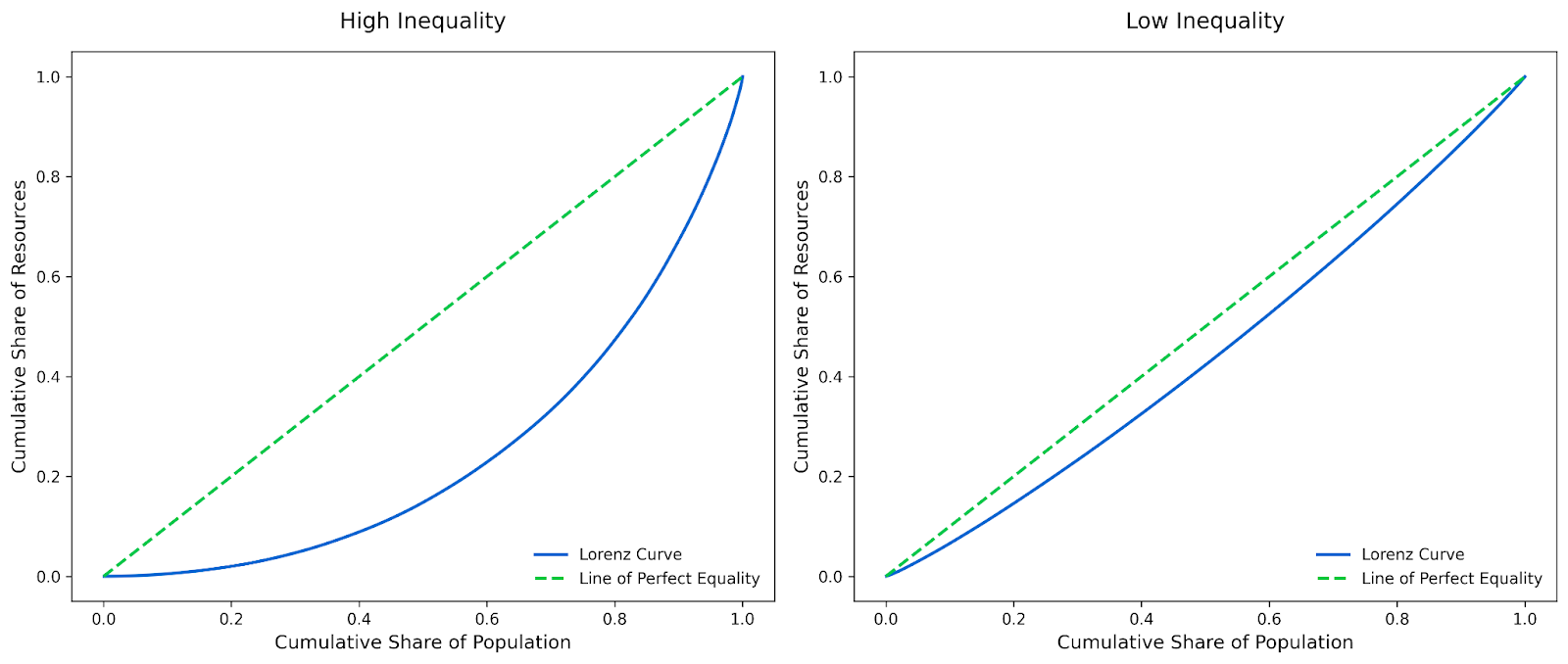
Cómo construir una curva de Lorenz
Vamos a construir juntos una curva de Lorenz con un ejemplo sencillo. Imagina que analizamos la distribución de la renta de una población pequeña.
Paso 1: Ordena los datos
El primer paso es organizar los datos en orden ascendente. Para este ejemplo, supongamos que tenemos los siguientes valores de ingresos para cinco individuos de una población: 20$, 30$, 50$, 80$, 100$.
Ordenaremos estos valores de menor a mayor. Esto garantiza que los porcentajes acumulados que calculemos después tengan sentido. Aquí tienes la tabla ordenada:
| Individual | Ingresos ($) |
|---|---|
| 1 | 120 |
| 2 | 230 |
| 3 | 350 |
| 4 | 480 |
| 5 | 5100 |
Paso 2: Calcular porcentajes acumulados
A continuación, calculamos los porcentajes acumulados tanto para la población (eje x) como para la renta (eje y).
- Para obtener el porcentaje de población acumulado, divide la posición de cada individuo en la lista ordenada por el número total de individuos. Por ejemplo, el primer individuo representa 1/5 (o 20%) de la población, el segundo representa 2/5 (40%), y así sucesivamente.
- Para el porcentaje de ingresos acumulados, suma los ingresos progresivamente y divide cada total acumulado por el total de ingresos globales. En este ejemplo, la renta total es de 280 $, por lo que la renta del primer individuo (20 $) representa 20/280 (o aproximadamente el 7,14%), y los dos primeros individuos juntos representan (20 + 30)/280 (aproximadamente el 17,86%).
Aquí tienes la tabla actualizada con los porcentajes acumulados:
| Individual | Ingresos ($) | Población acumulada (%) | Ingresos acumulados (%) |
|---|---|---|---|
| 120 | 20 | 20% | 7.14% |
| 230 | 30 | 40% | 17.86% |
| 350 | 50 | 60% | 35.71% |
| 480 | 80 | 80% | 64.29% |
| 5100 | 100 | 100% | 100% |
Paso 3: Traza la distribución acumulativa
Ahora que tenemos los porcentajes acumulados, podemos representarlos en un gráfico.
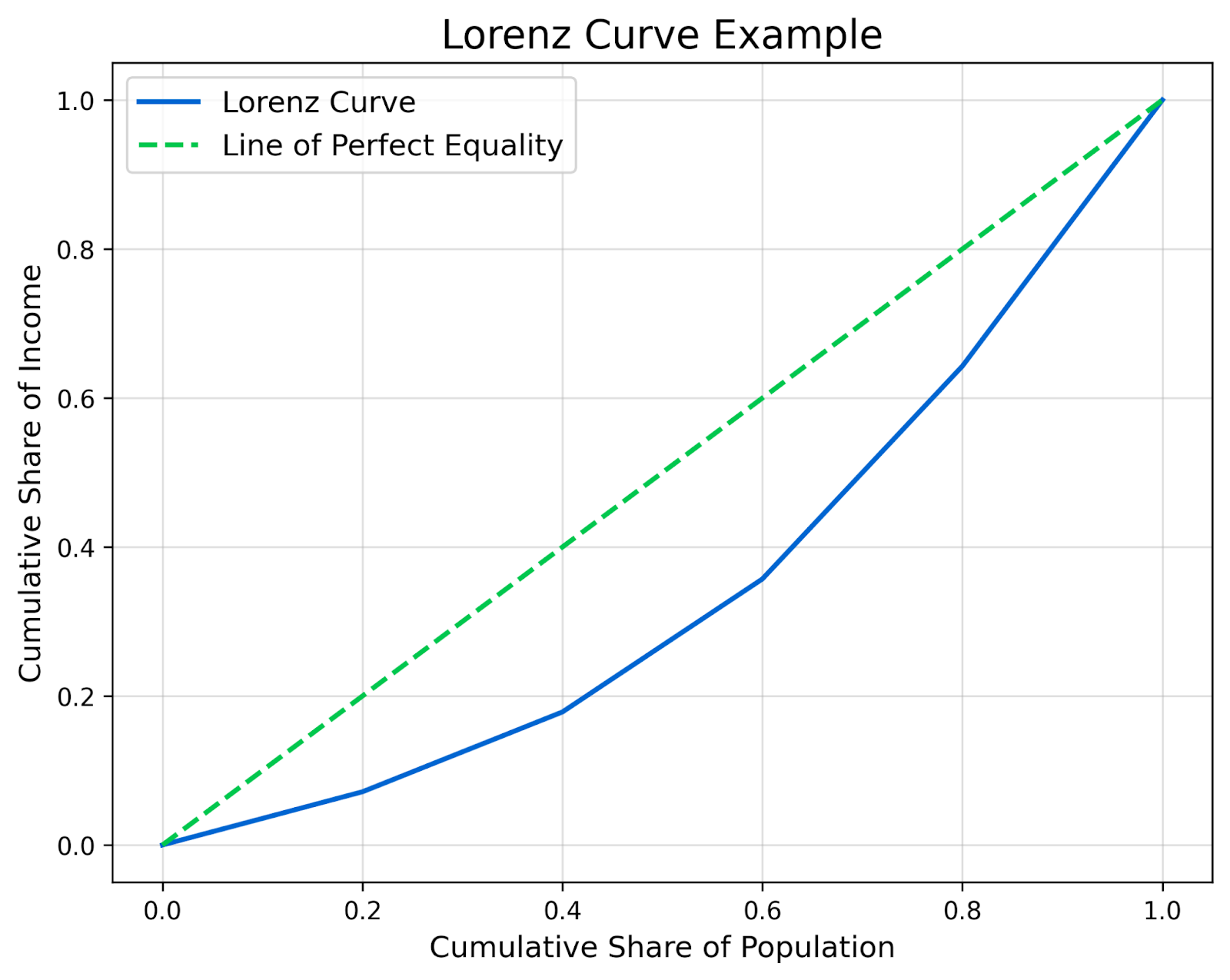
El eje de abscisas representa la parte acumulada de la población, y el eje de ordenadas representa la parte acumulada de la renta. Cada fila de la tabla corresponde a un punto del gráfico. Una vez trazados los puntos, conéctalos para formar la curva de Lorenz. A continuación, añade la línea de la igualdad perfecta.
Paso 4: Interpreta la curva de Lorenz
La curva de Lorenz resultante muestra la distribución real de la renta en esta población. Cuanto más se aleje la curva de la línea diagonal, mayor será la desigualdad. Como puedes ver en este ejemplo, la curva se curva notablemente porque el 20% de la población más pobre sólo posee el 7,14% de la renta.
Requisitos y retos de los datos
Para construir una curva de Lorenz precisa, necesitarás datos de alta calidad que cumplan algunos criterios clave. La calidad y la estructura de tus datos influirán directamente en la precisión y fiabilidad de tus resultados.
En primer lugar, el tamaño de la muestra es un factor crítico. Los conjuntos de datos pequeños pueden dar lugar a resultados engañosos, ya que pueden no captar toda la gama de desigualdades de una población. En nuestro ejemplo se utilizó un conjunto de datos demasiado pequeño, de sólo 5 individuos. Esta curva está diseñada para poblaciones enteras. Los conjuntos de datos más grandes proporcionan una imagen más fiable y representativa de la desigualdad, haciendo que tu curva de Lorenz sea más precisa.
La granularidad también es importante, porque cuanto más detallados sean tus datos, más precisa será tu curva de Lorenz. Por ejemplo, la renta de las personas o de los hogares te dará una mejor idea de la desigualdad en una población que la renta de condados enteros. Este último conjunto de datos puede ocultar muchas desigualdades.
Como en la mayoría de los análisis, los datos incompletos son un problema común que puede distorsionar significativamente la curva de Lorenz. Los valores omitidos crean lagunas en los porcentajes acumulados, lo que puede dar lugar a resultados inexactos. Antes de construir tu curva, asegúrate de que tu conjunto de datos es lo más completo posible, y considera cuidadosamente cómo tratas los datos que faltan. Si no estás seguro de cómo tratar los datos que faltan, consulta nuestro curso muy útil Cómo tratar los datos que faltan en Python.
Ejemplo práctico de código Python
Ahora que ya conocemos los fundamentos, exploremos cómo puede utilizarse la curva de Lorenz como herramienta narrativa más allá de los datos sobre la renta.
En este ejemplo, analizaremos los datos sobre delincuencia para comprender la desigualdad en la distribución de los delitos denunciados en los distintos barrios de una ciudad. Esto demostrará cómo puede aplicarse la curva de Lorenz a campos como la política pública.
Utilizaremos un conjunto de datos reales de la base de datos de delitos del Departamento de Policía de Chicago, que está disponible gratuitamente en Internet. Puedes descargar el conjunto de datos del Portal de Datos de Chicago. Este conjunto de datos contiene información detallada sobre los delitos denunciados en Chicago, incluido el tipo de delito, el lugar y la fecha.
A continuación, recorreremos los pasos para limpiar los datos, calcular la curva de Lorenz y visualizarla utilizando Python. Si eres nuevo en Python, te recomiendo nuestro curso Introducción a Python como una forma rápida de aprender el lenguaje.
En primer lugar, vamos a instalar todas las bibliotecas que necesitaremos para este ejemplo:
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltPaso 1: Descarga y carga el conjunto de datos
El código siguiente debería descargar el conjunto de datos del Portal de Datos de Chicago como un archivo CSV y cargarlo en Python utilizando pandas.
# Load the dataset
url = "<https://data.cityofchicago.org/resource/ijzp-q8t2.csv?$limit=100000>" # Limit to 100,000 rows for simplicity
data = pd.read_csv(url)Paso 2: Datos agregados de delincuencia por barrios
Este conjunto de datos contiene una columna para las zonas comunitarias, o barrios. Agruparemos los datos por esta columna para calcular el número total de delitos denunciados en cada barrio.
# Group by community area and count the number of crimes
crime_counts = data.groupby("community_area").size().reset_index(name="crime_count")
# Drop rows with missing community area values
crime_counts = crime_counts.dropna()
# Sort by crime count
crime_counts = crime_counts.sort_values(by="crime_count").reset_index(drop=True)
# Display the aggregated data
print(crime_counts.head())Output:
community_area crime_count
0 47.0 102
1 9.0 102
2 12.0 195
3 74.0 212
4 37.0 246Paso 3: Calcular porcentajes acumulados
Para construir la curva de Lorenz, necesitamos calcular el porcentaje acumulado de barrios y el porcentaje acumulado de delitos.
# Calculate cumulative percentages
crime_counts["cumulative_crime"] = crime_counts["crime_count"].cumsum()
crime_counts["cumulative_crime_percentage"] = crime_counts["cumulative_crime"] / crime_counts["crime_count"].sum()
crime_counts["cumulative_population_percentage"] = (np.arange(1, len(crime_counts) + 1)) / len(crime_counts)
# Display the updated data
print(crime_counts.head())Output:
community_area crime_count cumulative_crime cumulative_crime_percentage \\
0 47.0 102 102 0.00102
1 9.0 102 204 0.00204
2 12.0 195 399 0.00399
3 74.0 212 611 0.00611
4 37.0 246 857 0.00857
cumulative_population_percentage
0 0.012987
1 0.025974
2 0.038961
3 0.051948
4 0.064935 Paso 4: Traza la curva de Lorenz
Ahora que tenemos los porcentajes acumulados, podemos trazar la curva de Lorenz. El eje x representa la proporción acumulada de barrios, y el eje y representa la proporción acumulada de delitos. Para añadir un toque regional, utilizaremos los colores de los Chicago Bears como inspiración para nuestra trama.
# Example data for cumulative percentages
# x represents the cumulative share of neighborhoods
# y represents the cumulative share of crimes
x = np.linspace(0, 1, 100) # Replace with actual data
y = x**2 # Replace with actual data
# Chicago Bears-inspired colors
blue = "#0065D1" # Lighter blue for the Lorenz curve
orange = "#FF5A1F" # Bright orange for the line of perfect equality
# Create the plot
plt.figure(figsize=(8, 6))
# Plot the Lorenz curve
# This curve shows the inequality in crime distribution across neighborhoods
plt.plot(x, y, label="Lorenz Curve", color=blue, linewidth=2)
# Plot the line of perfect equality
# This line represents a hypothetical scenario where crimes are evenly distributed
plt.plot([0, 1], [0, 1], label="Line of Perfect Equality", color=orange, linestyle="--", linewidth=2)
# Add a title to explain what the graph represents
plt.title("Lorenz Curve of Crime Distribution Across Chicago Neighborhoods", fontsize=16, color="black", pad=15)
# Label the x-axis to show what the horizontal axis represents
plt.xlabel("Cumulative Share of Neighborhoods", fontsize=12, color="black", labelpad=10)
# Label the y-axis to show what the vertical axis represents
plt.ylabel("Cumulative Share of Crimes", fontsize=12, color="black", labelpad=10)
# Add a legend to explain the two lines
plt.legend(fontsize=12, loc="lower right", frameon=False)
# Remove the grid for a cleaner look
plt.grid(False)
# Set the background color to white for a professional appearance
plt.gca().set_facecolor("white")
# Remove the top and right borders of the graph for a minimalist design
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
# Save the plot as a PNG file
# This saves the graph as an image file for sharing or embedding in reports
plt.savefig("lorenz_curve_crime.png", dpi=300, bbox_inches="tight")
# Display the plot
plt.show()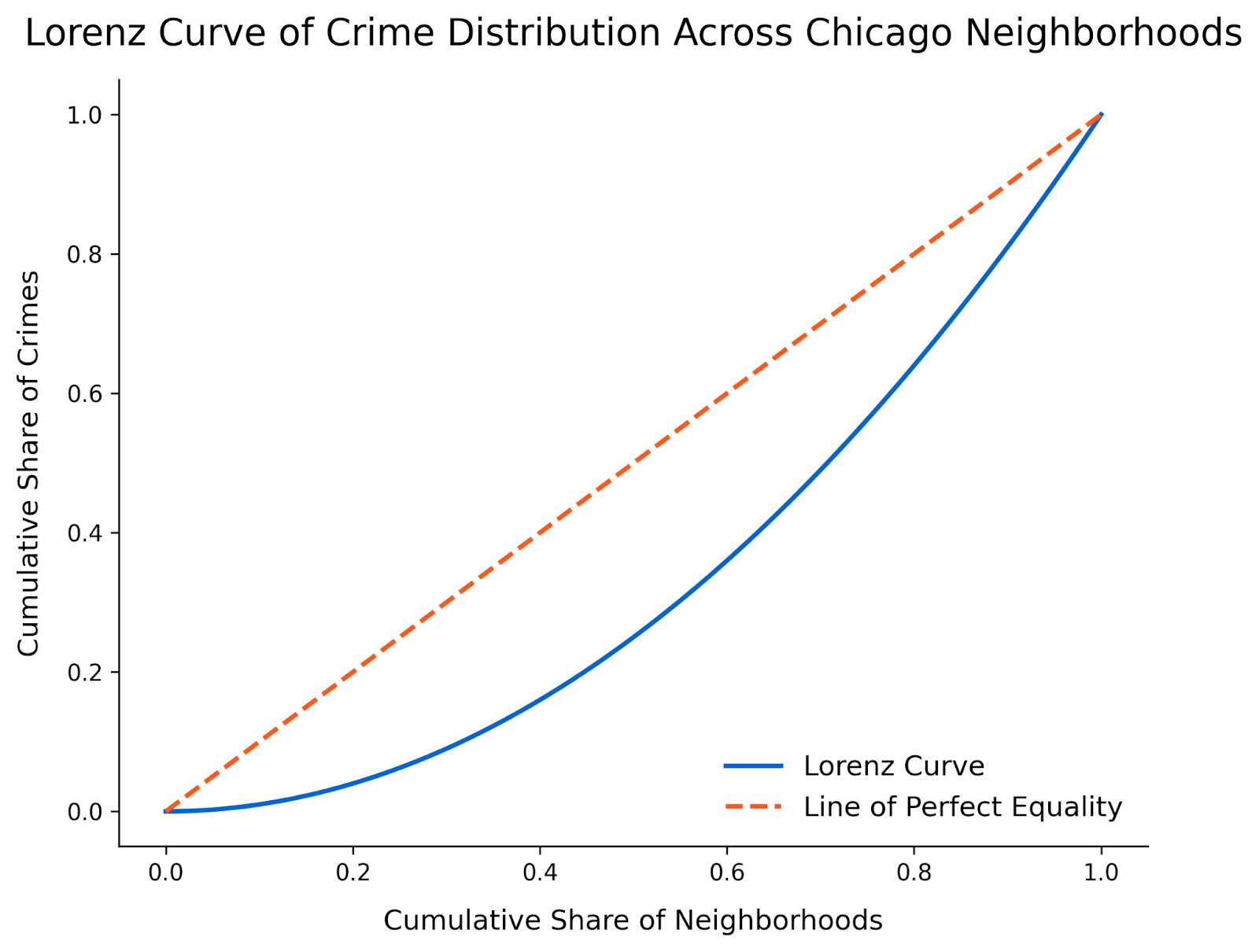
Paso 5: Interpreta los resultados
Por último, tenemos que interpretar la trama. Esta curva de Lorenz revela una sorprendente desigualdad en la distribución de los delitos entre los barrios de Chicago. La curva se aleja significativamente de la línea de igualdad perfecta, lo que demuestra que una pequeña fracción de barrios representa la mayoría de los delitos denunciados.
Parece que el primer 50% de los barrios contribuyen a menos del 20% de los delitos totales, mientras que los barrios restantes soportan la mayor parte de la carga delictiva. Esta visualización pone de relieve pautas de desigualdad que podrían no ser tan evidentes en otros tipos de gráficos. El siguiente paso puede ser identificar los barrios con mayor delincuencia para poner en marcha medidas paliativas o identificar los barrios con menos delincuencia para ver qué elementos disuasorios funcionan.
Este ejemplo demuestra cómo la curva de Lorenz puede aplicarse más allá de los datos sobre ingresos para contar historias convincentes sobre la desigualdad en otros campos. Analizando los datos sobre delincuencia, podemos descubrir pautas de desigualdad que informen las decisiones de política pública y planificación urbana. Prueba a aplicar este método a otros conjuntos de datos, como el acceso a la sanidad, los resultados educativos o los datos medioambientales, para explorar la desigualdad de formas nuevas y significativas.
La Curva de Lorenz frente al Coeficiente de Gini
El coeficiente de Gini se obtiene directamente de la curva de Lorenz. Mide el área entre la curva de Lorenz y la línea de igualdad perfecta. Un área mayor indica mayor desigualdad, mientras que un área menor sugiere mayor igualdad. El coeficiente de Gini oscila entre 0 y 1, donde 0 representa la igualdad perfecta (todos tienen los mismos recursos) y 1 representa la desigualdad extrema (un individuo posee todos los recursos).
La medida que utilices depende de tus objetivos. La curva de Lorenz muestra la forma de la desigualdad, mientras que el coeficiente de Gini proporciona un resumen numérico de la misma. Si estás estudiando el grado de desigualdad dentro de una población, la curva de Lorenz te ofrecerá más detalles. Sin embargo, si estás comparando muchas poblaciones entre sí, comparar las curvas de Lorenz de cada una puede resultar engorroso, por lo que el coeficiente de Gini puede ser más apropiado. Para profundizar en el coeficiente de Gini, consulta mi tutorial Comprender el coeficiente de Gini.
Además, debemos decir que la curva de Lorenz es quizá más flexible, ya que puede aplicarse a diversos tipos de datos, como la renta, la delincuencia, el acceso a la sanidad o la biodiversidad, y utilizarse para comparar distribuciones a lo largo del tiempo o entre grupos. El coeficiente de Gini también puede utilizarse para este tipo de comparaciones, pero tiene fama de utilizarse principalmente para medir la desigualdad de ingresos. Esto puede crear un sesgo para algunos consumidores. Según mi experiencia, las personas suelen tener menos prejuicios cuando interpretan gráficos que cuando se les da un número.
| Función | Curva de Lorenz | Coeficiente de Gini |
|---|---|---|
| Propósito | Muestra la distribución de los recursos en una población | Resume la desigualdad en un único valor |
| Tipo | Representación visual | Representación numérica |
| Interpretación | La forma de la curva indica el grado de desigualdad | El valor oscila entre 0 (igualdad perfecta) y 1 (desigualdad extrema) |
| Casos prácticos | Comparar distribuciones, identificar patrones y comunicar los resultados | Comparar los niveles de desigualdad entre conjuntos de datos o poblaciones |
| Flexibilidad | Puede aplicarse a diversos conjuntos de datos (por ejemplo, renta, delincuencia, biodiversidad) | Se utiliza principalmente para la desigualdad de ingresos o de riqueza |
| Accionabilidad | Ayuda a identificar áreas específicas de desigualdad para intervenciones específicas | Proporciona un resumen de alto nivel para realizar comparaciones generales |
La comparación anterior pone de manifiesto cómo se complementan la curva de Lorenz y el coeficiente de Gini. La curva de Lorenz ofrece una perspectiva más detallada y visual para una población, mientras que el coeficiente de Gini proporciona un resumen conciso que puede utilizarse para comparar entre poblaciones.
Aplicaciones reales de la curva de Lorenz
La curva de Lorenz es una herramienta versátil que se ha aplicado en una amplia gama de campos. Exploremos algunas de sus aplicaciones más impactantes.
- La curva de Lorenz en economía y finanzas: La Curva de Lorenz se utiliza sobre todo para analizar la desigualdad de ingresos y riqueza. Los economistas y los responsables políticos se basan en ella para comprender cómo se distribuyen los recursos dentro de una población y para diseñar intervenciones como políticas fiscales o programas sociales.
- La curva de Lorenz en salud pública y epidemiología: En salud pública, la curva de Lorenz puede utilizarse para medir las desigualdades en los resultados sanitarios o en el acceso a la atención sanitaria. Esto ayuda a los investigadores y a los responsables políticos a identificar las disparidades y a asignar los recursos de forma más eficaz.
- La curva de Lorenz en ecología y biodiversidad: Los ecólogos pueden utilizar la curva de Lorenz para estudiar la distribución y abundancia de las especies. Puede ayudar a cuantificar la biodiversidad y a identificar ecosistemas en los que dominan unas pocas especies mientras que otras son escasas.
- La curva de Lorenz en la ciencia de datos y el aprendizaje automático: La curva de Lorenz se utiliza cada vez más en la ciencia de datos para analizar distribuciones y evaluar la equidad en los modelos predictivos. Un ejemplo de ello es la analítica de clientes. Las empresas pueden utilizar la curva de Lorenz para comprender la concentración de ingresos entre los clientes. Puede ayudar a identificar qué usuarios generan la mayor parte de los ingresos, informando potencialmente las estrategias de marketing o los programas de fidelización.
- La curva de Lorenz en la ciencia de datos y el aprendizaje automático: Otro ejemplo que me sorprendió conocer es el del aprendizaje automático. La curva de Lorenz puede ayudar a los científicos de datos a evaluar si las predicciones de un modelo están sesgadas. Por ejemplo, en un modelo de aprobación de préstamos, la curva podría revelar que un pequeño grupo de solicitantes recibe la mayoría de las aprobaciones, lo que indicaría un posible sesgo en el algoritmo.
Ventajas y limitaciones de la curva de Lorenz
Como cualquier método, la curva de Lorenz tiene sus puntos fuertes y débiles.
Limitaciones de la curva de Lorenz
La curva de Lorenz suele requerir datos bastante granulares para producir resultados significativos. Los conjuntos de datos agregados o incompletos a veces pueden llevar a conclusiones inexactas. Por ejemplo, los datos sobre ingresos que excluyen los ingresos informales, como las propinas, pueden subestimar la desigualdad.
También es importante tener un tamaño de muestra lo suficientemente grande para garantizar una curva en lugar de una línea irregular, como puedes ver en la primera figura. Como siempre, es importante que te asegures de que tus datos son lo más completos posible. Y, por supuesto, debes validar cuidadosamente tus datos y documentar cualquier suposición realizada para garantizar la transparencia y la fiabilidad.
La curva de Lorenz tampoco capta la desigualdad multidimensional. Se centra en una sola variable, como la renta o la riqueza, y no tiene en cuenta ningún efecto combinado. Sin embargo, si quieres medir la desigualdad multidimensional, hay otras herramientas que puedes utilizar, como el Índice de Pobreza Multidimensional.
Ventajas de la curva de Lorenz
La mayor ventaja de la curva de Lorenz, en mi opinión, es que proporciona una representación visual intuitiva de la desigualdad, lo que facilita su comprensión de un vistazo. Al comparar la curva con la línea de la igualdad perfecta, las disparidades dentro de una población se ponen inmediatamente de manifiesto. Es una herramienta de narración visual que hace que los datos sobre desigualdad sean accesibles tanto para el público técnico como para el no técnico.
Su versatilidad es su otra gran ventaja. La curva de Lorenz puede aplicarse en diversos campos, desde la economía y la salud pública hasta la ecología y el aprendizaje automático. Esta flexibilidad hace que sea ampliamente útil.
Conclusión
La curva de Lorenz es una herramienta narrativa versátil, útil para mostrar y comprender la desigualdad. Si este tipo de visualización te interesa, puede que disfrutes leyendo Media geométrica: Una medida para el crecimiento y la capitalización. O, si quieres aprender más sobre finanzas, te animo a que eches un vistazo a nuestro curso Introducción a Python para las Finanzas y a nuestro itinerario de habilidades Finanzas Aplicadas en Python.
