Cursus
L'inégalité est un sujet qui touche presque tous les aspects de la vie : les revenus, la richesse, la santé, l'éducation et même la manière dont les ressources sont réparties dans les écosystèmes. Mais comment la mesurer concrètement ? La courbe de Lorenz est l'un des outils les plus puissants que j'ai trouvés pour visualiser les inégalités.
Bien qu'elle soit couramment utilisée pour mesurer les inégalités de revenus, la courbe de Lorenz n'est pas réservée aux économistes. Au fil du temps, elle est devenue un outil polyvalent utilisé pour examiner les disparités en matière de soins de santé, pour étudier la biodiversité et même dans l'apprentissage automatique pour évaluer l'équité des modèles prédictifs. Pour les scientifiques des données, c'est un excellent moyen de raconter une histoire sur l'inégalité dans un ensemble de données.
Dans ce tutoriel, je vous montrerai comment fonctionne la courbe de Lorenz. Nous verrons comment le créer avec votre jeu de données, à l'aide de Python, et vous apprendrez à l'utiliser dans vos propres projets. Si vous souhaitez quantifier les inégalités de revenus, analyser la segmentation de la clientèle ou étudier l'affectation des ressources, la courbe de Lorenz peut vous aider à communiquer ces idées complexes à l'aide d'un simple visuel.
Comprendre la courbe de Lorenz
La courbe de Lorenz a été introduite en 1905 par l'économiste Max O. Lorenz. La méthode consiste à comparer la distribution réelle d'une ressource à une ligne d'égalité parfaite hypothétique (une ligne où tout le monde dispose d'une quantité égale). Plus la courbe s'éloigne de cette ligne d'égalité parfaite, plus l'inégalité dans la distribution de cette ressource particulière est grande.
Structure de la courbe de Lorenz
La courbe de Lorenz a une structure simple. Sur l'axe des abscisses, nous représentons la part cumulée de la population, en commençant par l'individu le plus pauvre et en allant vers l'individu le plus riche. L'axe des ordonnées indique la part cumulée de la ressource mesurée.
Ensuite, nous devons ajouter la ligne d'égalité parfaite, qui est une ligne diagonale allant du coin inférieur gauche au coin supérieur droit. Cette ligne représente un scénario dans lequel tout le monde dispose d'une part égale de la ressource qui nous intéresse.
La courbe de Lorenz elle-même montre la distribution réelle de la ressource. Plus la courbe s'éloigne de la ligne d'égalité parfaite, plus l'inégalité qu'elle représente est importante.
Comment interpréter la courbe de Lorenz
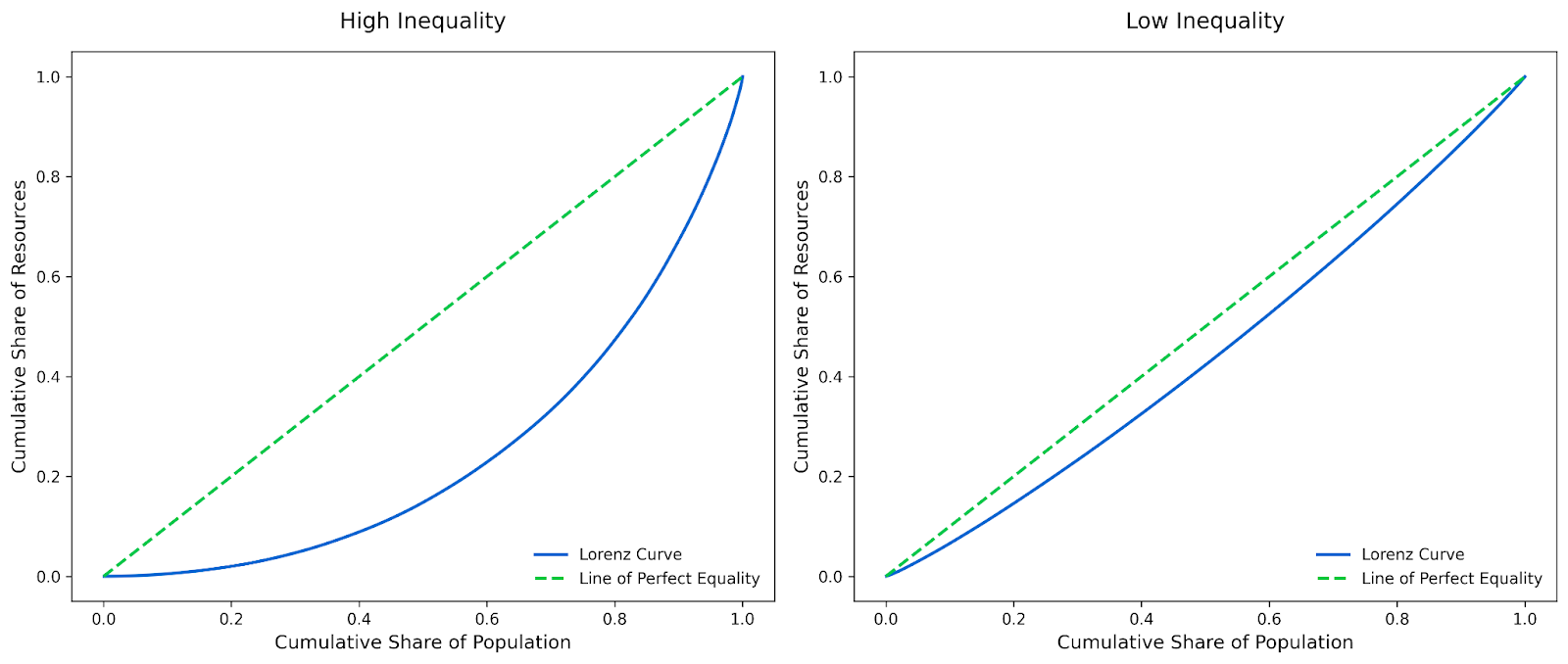
Si la courbe de Lorenz est proche de la diagonale de l'égalité parfaite, cela signifie que la ressource est répartie de manière relativement homogène. Par exemple, dans une société où les 50 % les plus pauvres de la population disposent d'environ 50 % des revenus, la courbe de Lorenz est plus proche de la diagonale. Cette courbe peu profonde indique une faible inégalité.
En revanche, si la courbe s'éloigne de la diagonale, cela indique une forte inégalité. Cela peut se produire si, par exemple, les 50 % les plus pauvres de la population ne disposent que de 10 % des revenus, tandis que les 10 % les plus riches disposent de tout le reste.
Comment construire une courbe de Lorenz
Voyons ensemble comment construire une courbe de Lorenz à l'aide d'un exemple simple. Imaginez que nous analysions la distribution des revenus d'une petite population.
Étape 1 : Trier les données
La première étape consiste à organiser les données par ordre croissant. Pour cet exemple, supposons que nous disposions des valeurs de revenu suivantes pour cinq individus d'une population : 20 $, 30 $, 50 $, 80 $, 100 $.
Nous allons trier ces valeurs de la plus petite à la plus grande. Cela garantit que les pourcentages cumulés que nous calculons par la suite ont un sens. Voici le tableau trié :
| Individuel | Revenu ($) |
|---|---|
| 1 | 120 |
| 2 | 230 |
| 3 | 350 |
| 4 | 480 |
| 5 | 5100 |
Étape 2 : Calculer les pourcentages cumulés
Ensuite, nous calculons les pourcentages cumulés pour la population (axe des x) et le revenu (axe des y).
- Pour obtenir le pourcentage de population cumulée, divisez la position de chaque individu dans la liste triée par le nombre total d'individus. Par exemple, le premier individu représente 1/5 (ou 20%) de la population, le deuxième représente 2/5 (40%), et ainsi de suite.
- Pour le pourcentage de revenu cumulé, additionnez progressivement les revenus et divisez chaque total cumulé par le total du revenu global. Dans cet exemple, le revenu total est de 280 $, de sorte que le revenu du premier individu (20 $) représente 20/280 (soit environ 7,14 %), et les deux premiers individus ensemble représentent (20 + 30)/280 (environ 17,86 %).
Voici le tableau mis à jour avec les pourcentages cumulés :
| Individuel | Revenu ($) | Population cumulée (%) | Revenu cumulé (%) |
|---|---|---|---|
| 120 | 20 | 20% | 7.14% |
| 230 | 30 | 40% | 17.86% |
| 350 | 50 | 60% | 35.71% |
| 480 | 80 | 80% | 64.29% |
| 5100 | 100 | 100% | 100% |
Étape 3 : Tracez la distribution cumulative
Maintenant que nous disposons des pourcentages cumulés, nous pouvons les représenter sur un graphique.
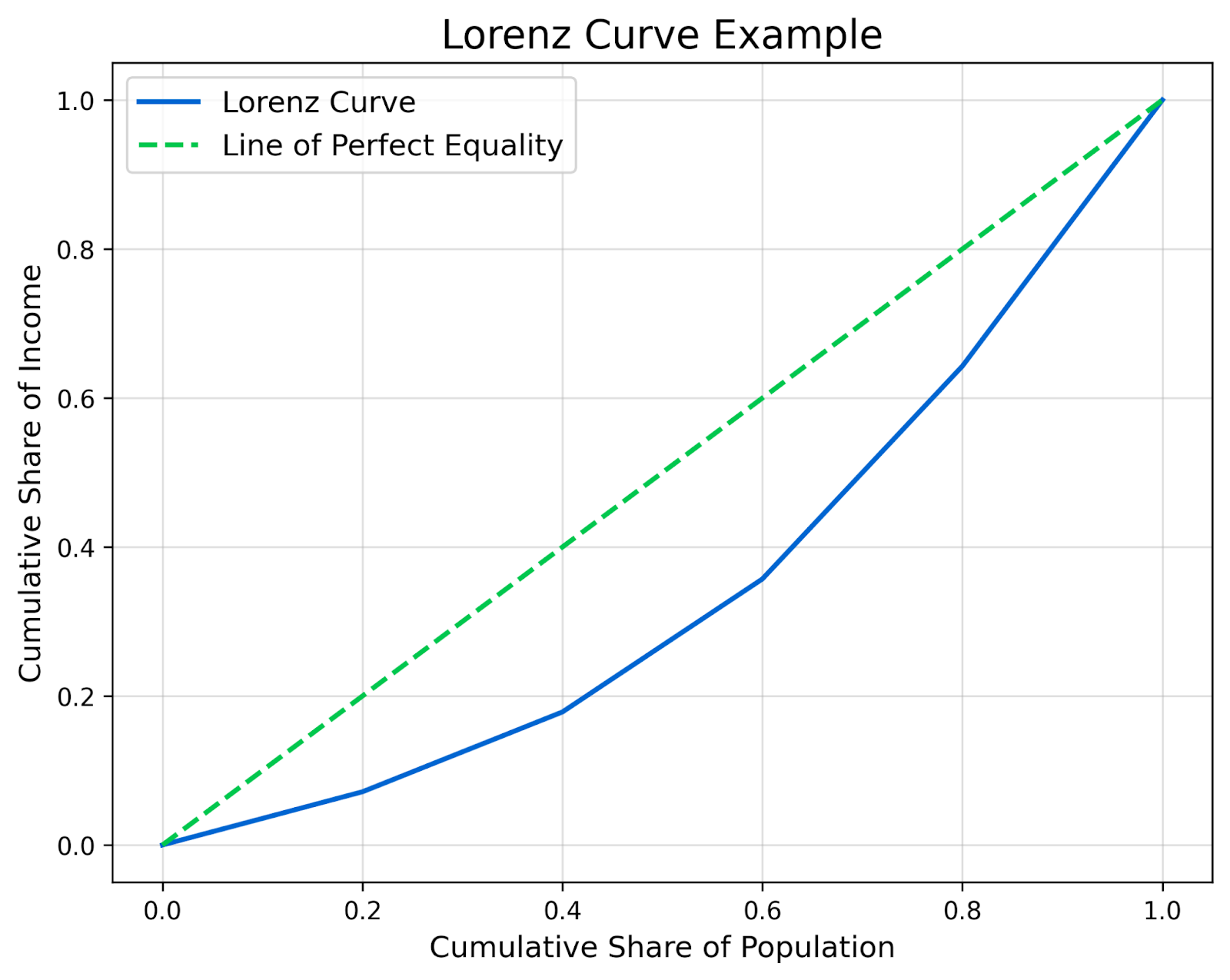
L'axe des x représente la part cumulée de la population et l'axe des y représente la part cumulée des revenus. Chaque ligne du tableau correspond à un point du graphique. Une fois les points tracés, reliez-les pour former la courbe de Lorenz. Ajoutez ensuite la ligne d'égalité parfaite.
Étape 4 : Interpréter la courbe de Lorenz
La courbe de Lorenz qui en résulte montre la distribution réelle des revenus dans cette population. Plus la courbe s'éloigne de la diagonale, plus l'inégalité est grande. Comme vous pouvez le voir dans cet exemple, la courbe s'infléchit sensiblement parce que les 20 % les plus pauvres de la population ne détiennent que 7,14 % des revenus.
Exigences et défis en matière de données
Pour construire une courbe de Lorenz précise, vous aurez besoin de données de haute qualité répondant à quelques critères clés. La qualité et la structure de vos données auront un impact direct sur la précision et la fiabilité de vos résultats.
Tout d'abord, la taille de l'échantillon est un facteur essentiel. Les petits ensembles de données peuvent conduire à des résultats trompeurs, car ils peuvent ne pas refléter l'ensemble des inégalités au sein d'une population. Dans notre exemple, nous avons utilisé un ensemble de données beaucoup trop petit, composé de seulement 5 individus. Cette courbe est conçue pour des populations entières. Des ensembles de données plus importants fournissent une image plus fiable et plus représentative des inégalités, ce qui rend votre courbe de Lorenz plus précise.
La granularité est également importante car plus vos données sont détaillées, plus votre courbe de Lorenz sera précise. Par exemple, le revenu des individus ou des ménages vous donnera une meilleure idée de l'inégalité au sein d'une population que le revenu de comtés entiers. Ce dernier ensemble de données peut cacher de nombreuses inégalités.
Comme dans la plupart des analyses, les données incomplètes sont un problème courant qui peut fausser considérablement la courbe de Lorenz. Les valeurs manquantes créent des lacunes dans les pourcentages cumulés, ce qui peut conduire à des résultats inexacts. Avant de construire votre courbe, assurez-vous que votre ensemble de données est aussi complet que possible et réfléchissez bien à la façon dont vous traiterez les données manquantes. Si vous ne savez pas comment gérer les données manquantes, consultez notre cours très utile Dealing with Missing Data in Python.
Exemple pratique de code Python
Maintenant que nous avons assimilé les principes de base, voyons comment la courbe de Lorenz peut être utilisée comme outil de narration au-delà des seules données sur les revenus.
Dans cet exemple, nous analyserons les données relatives à la criminalité afin de comprendre les inégalités dans la répartition des délits signalés dans les différents quartiers d'une ville. Cela démontrera comment la courbe de Lorenz peut être appliquée à des domaines tels que la politique publique.
Nous utiliserons un ensemble de données réelles provenant de la base de données criminelles du département de la police de Chicago, qui est librement accessible en ligne. Vous pouvez télécharger l'ensemble des données sur le portail de données de Chicago. Ce jeu de données contient des informations détaillées sur les délits signalés à Chicago, y compris le type de délit, le lieu et la date.
Ci-dessous, nous allons parcourir les étapes pour nettoyer les données, calculer la courbe de Lorenz et la visualiser à l'aide de Python. Si vous ne connaissez pas Python, je vous recommande notre cours d'introduction à Python comme moyen rapide d'apprendre le langage.
Tout d'abord, installons toutes les bibliothèques dont nous aurons besoin pour cet exemple :
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltÉtape 1 : Téléchargez et chargez l'ensemble de données
Le code ci-dessous doit télécharger le jeu de données du Chicago Data Portal sous forme de fichier CSV et le charger dans Python à l'aide de pandas.
# Load the dataset
url = "<https://data.cityofchicago.org/resource/ijzp-q8t2.csv?$limit=100000>" # Limit to 100,000 rows for simplicity
data = pd.read_csv(url)Étape 2 : Données agrégées sur la criminalité par quartier
Ce jeu de données contient une colonne pour les zones communautaires, ou quartiers. Nous regrouperons les données en fonction de cette colonne pour calculer le nombre total de délits signalés dans chaque quartier.
# Group by community area and count the number of crimes
crime_counts = data.groupby("community_area").size().reset_index(name="crime_count")
# Drop rows with missing community area values
crime_counts = crime_counts.dropna()
# Sort by crime count
crime_counts = crime_counts.sort_values(by="crime_count").reset_index(drop=True)
# Display the aggregated data
print(crime_counts.head())Output:
community_area crime_count
0 47.0 102
1 9.0 102
2 12.0 195
3 74.0 212
4 37.0 246Étape 3 : Calculer les pourcentages cumulés
Pour construire la courbe de Lorenz, nous devons calculer le pourcentage cumulé de quartiers et le pourcentage cumulé de crimes.
# Calculate cumulative percentages
crime_counts["cumulative_crime"] = crime_counts["crime_count"].cumsum()
crime_counts["cumulative_crime_percentage"] = crime_counts["cumulative_crime"] / crime_counts["crime_count"].sum()
crime_counts["cumulative_population_percentage"] = (np.arange(1, len(crime_counts) + 1)) / len(crime_counts)
# Display the updated data
print(crime_counts.head())Output:
community_area crime_count cumulative_crime cumulative_crime_percentage \\
0 47.0 102 102 0.00102
1 9.0 102 204 0.00204
2 12.0 195 399 0.00399
3 74.0 212 611 0.00611
4 37.0 246 857 0.00857
cumulative_population_percentage
0 0.012987
1 0.025974
2 0.038961
3 0.051948
4 0.064935 Étape 4 : Tracer la courbe de Lorenz
Maintenant que nous disposons des pourcentages cumulés, nous pouvons tracer la courbe de Lorenz. L'axe des x représente la part cumulée des quartiers et l'axe des y représente la part cumulée des délits. Pour ajouter une touche régionale, nous nous inspirerons des couleurs des Chicago Bears.
# Example data for cumulative percentages
# x represents the cumulative share of neighborhoods
# y represents the cumulative share of crimes
x = np.linspace(0, 1, 100) # Replace with actual data
y = x**2 # Replace with actual data
# Chicago Bears-inspired colors
blue = "#0065D1" # Lighter blue for the Lorenz curve
orange = "#FF5A1F" # Bright orange for the line of perfect equality
# Create the plot
plt.figure(figsize=(8, 6))
# Plot the Lorenz curve
# This curve shows the inequality in crime distribution across neighborhoods
plt.plot(x, y, label="Lorenz Curve", color=blue, linewidth=2)
# Plot the line of perfect equality
# This line represents a hypothetical scenario where crimes are evenly distributed
plt.plot([0, 1], [0, 1], label="Line of Perfect Equality", color=orange, linestyle="--", linewidth=2)
# Add a title to explain what the graph represents
plt.title("Lorenz Curve of Crime Distribution Across Chicago Neighborhoods", fontsize=16, color="black", pad=15)
# Label the x-axis to show what the horizontal axis represents
plt.xlabel("Cumulative Share of Neighborhoods", fontsize=12, color="black", labelpad=10)
# Label the y-axis to show what the vertical axis represents
plt.ylabel("Cumulative Share of Crimes", fontsize=12, color="black", labelpad=10)
# Add a legend to explain the two lines
plt.legend(fontsize=12, loc="lower right", frameon=False)
# Remove the grid for a cleaner look
plt.grid(False)
# Set the background color to white for a professional appearance
plt.gca().set_facecolor("white")
# Remove the top and right borders of the graph for a minimalist design
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
# Save the plot as a PNG file
# This saves the graph as an image file for sharing or embedding in reports
plt.savefig("lorenz_curve_crime.png", dpi=300, bbox_inches="tight")
# Display the plot
plt.show()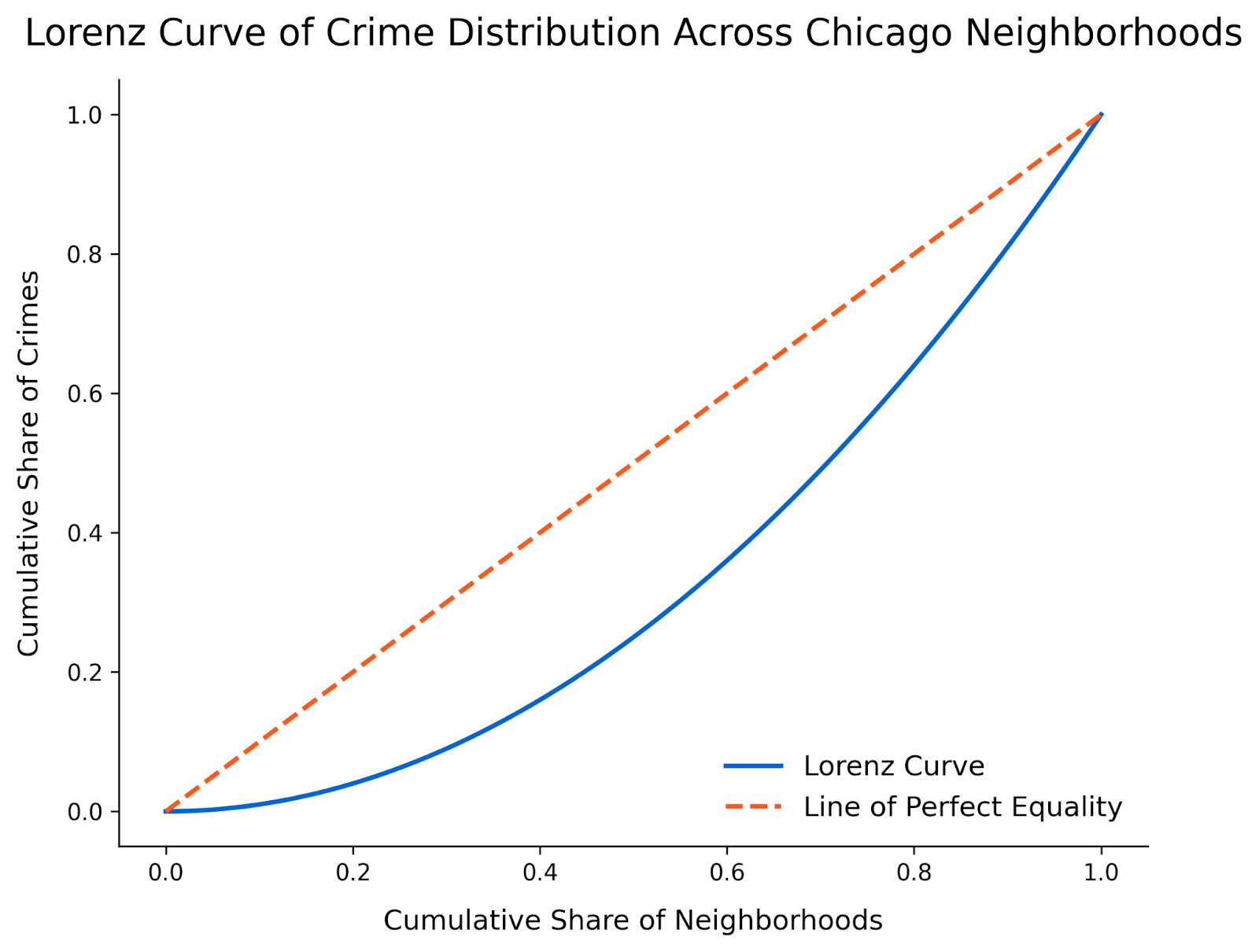
Étape 5 : Interpréter les résultats
Enfin, nous devons interpréter le graphique. Cette courbe de Lorenz révèle une inégalité frappante dans la répartition des délits entre les quartiers de Chicago. La courbe s'éloigne considérablement de la ligne d'égalité parfaite, ce qui montre qu'une petite fraction de quartiers est à l'origine de la majorité des délits signalés.
Il semble que les premiers 50 % des quartiers contribuent à moins de 20 % du total des délits, tandis que les autres quartiers supportent l'essentiel du fardeau de la criminalité. Cette visualisation met en évidence des modèles d'inégalité qui pourraient ne pas être aussi apparents dans d'autres types de graphiques. L'étape suivante peut consister à identifier les quartiers où la criminalité est la plus élevée afin de mettre en place des mesures d'atténuation ou d'identifier les quartiers où la criminalité est la moins élevée afin de voir quels sont les moyens de dissuasion qui fonctionnent.
Cet exemple montre comment la courbe de Lorenz peut être appliquée au-delà des données sur les revenus pour raconter des histoires convaincantes sur l'inégalité dans d'autres domaines. L'analyse des données relatives à la criminalité permet de mettre en évidence des schémas d'inégalité qui éclairent les politiques publiques et les décisions d'urbanisme. Essayez d'appliquer cette méthode à d'autres ensembles de données, tels que l'accès aux soins de santé, les résultats scolaires ou les données environnementales, afin d'explorer les inégalités d'une manière nouvelle et significative.
La courbe de Lorenz et le coefficient de Gini
Le coefficient de Gini est directement dérivé de la courbe de Lorenz. Il mesure la zone entre la courbe de Lorenz et la ligne d'égalité parfaite. Une zone plus grande indique une plus grande inégalité, tandis qu'une zone plus petite suggère une plus grande égalité. Le coefficient de Gini varie de 0 à 1, où 0 représente l'égalité parfaite (tout le monde a les mêmes ressources), et 1 représente l'inégalité extrême (un seul individu détient toutes les ressources).
Le choix de la mesure dépend de vos objectifs. La courbe de Lorenz montre la forme de l'inégalité, tandis que le coefficient de Gini en fournit un résumé numérique. Si vous étudiez l'ampleur des inégalités au sein d'une population, la courbe de Lorenz sera plus détaillée. Toutefois, si vous comparez de nombreuses populations entre elles, la comparaison des courbes de Lorenz de chacune d'entre elles peut s'avérer fastidieuse, de sorte que le coefficient de Gini peut s'avérer plus approprié. Pour en savoir plus sur le coefficient de Gini, consultez mon tutoriel Comprendre le coefficient de Gini.
Il convient également de préciser que la courbe de Lorenz est peut-être plus flexible, car elle peut être appliquée à différents types de données, notamment les revenus, la criminalité, l'accès aux soins de santé ou la biodiversité, et être utilisée pour comparer les distributions dans le temps ou entre les groupes. Le coefficient de Gini peut également être utilisé pour ce type de comparaisons, mais il a la réputation d'être principalement utilisé pour mesurer l'inégalité des revenus. Cela peut créer un biais pour certains consommateurs. D'après mon expérience, les gens ont tendance à avoir moins de préjugés lorsqu'ils interprètent des graphiques que lorsqu'on leur donne un chiffre.
| Fonctionnalité | Courbe de Lorenz | Coefficient de Gini |
|---|---|---|
| Objectif | Indique la répartition des ressources au sein d'une population | Résume l'inégalité en une seule valeur |
| Type | Représentation visuelle | Représentation numérique |
| Interprétation | La forme de la courbe indique le degré d'inégalité | La valeur est comprise entre 0 (égalité parfaite) et 1 (inégalité extrême). |
| Cas d'utilisation | Comparer les distributions, identifier les modèles et communiquer les résultats. | Comparer les niveaux d'inégalité entre les ensembles de données ou les populations |
| Flexibilité | Peut être appliqué à divers ensembles de données (par exemple, revenus, criminalité, biodiversité). | Principalement utilisé pour l'inégalité des revenus ou des richesses |
| Capacité d'action | Permet d'identifier des domaines spécifiques d'inégalité pour des interventions ciblées | Fournit un résumé de haut niveau permettant des comparaisons générales |
La comparaison ci-dessus met en évidence la complémentarité de la courbe de Lorenz et du coefficient de Gini. La courbe de Lorenz offre une perspective plus détaillée et visuelle pour une population, tandis que le coefficient de Gini fournit un résumé concis qui peut être utilisé pour comparer les populations.
Applications de la courbe de Lorenz dans le monde réel
La courbe de Lorenz est un outil polyvalent qui a été utilisé dans un grand nombre de domaines. Examinons quelques-unes de ses applications les plus marquantes.
- La courbe de Lorenz en économie et en finance: La courbe de Lorenz est surtout utilisée pour analyser les inégalités de revenus et de richesses. Les économistes et les décideurs politiques s'appuient sur ces données pour comprendre comment les ressources sont réparties au sein d'une population et pour concevoir des interventions telles que des politiques fiscales ou des programmes sociaux.
- La courbe de Lorenz en santé publique et en épidémiologie: En santé publique, la courbe de Lorenz peut être utilisée pour mesurer les inégalités en matière de santé ou d'accès aux soins. Cela permet aux chercheurs et aux décideurs politiques d'identifier les disparités et d'allouer les ressources de manière plus efficace.
- La courbe de Lorenz en écologie et en biodiversité: Les écologistes peuvent utiliser la courbe de Lorenz pour étudier la distribution et l'abondance des espèces. Elle permet de quantifier la biodiversité et d'identifier les écosystèmes où quelques espèces dominent tandis que d'autres sont rares.
- La courbe de Lorenz dans la science des données et l'apprentissage automatique: La courbe de Lorenz est de plus en plus utilisée en science des données pour analyser les distributions et évaluer l'équité des modèles prédictifs. L'analyse de la clientèle en est un exemple. Les entreprises peuvent utiliser la courbe de Lorenz pour comprendre la concentration des revenus parmi les clients. Il peut aider à identifier les utilisateurs qui génèrent le plus de revenus, ce qui peut permettre d'élaborer des stratégies de marketing ou des programmes de fidélisation.
- La courbe de Lorenz dans la science des données et l'apprentissage automatique: Un autre exemple qui m'a surpris est celui de l'apprentissage automatique. La courbe de Lorenz peut aider les scientifiques à déterminer si les prédictions d'un modèle sont biaisées. Par exemple, dans un modèle d'approbation de prêt, la courbe peut révéler qu'un petit groupe de demandeurs reçoit la majorité des approbations, ce qui indique un biais potentiel dans l'algorithme.
Avantages et limites de la courbe de Lorenz
Comme toute méthode, la courbe de Lorenz a ses forces et ses faiblesses.
Limites de la courbe de Lorenz
La courbe de Lorenz nécessite souvent des données assez granulaires pour produire des résultats significatifs. Des ensembles de données agrégées ou incomplètes peuvent parfois conduire à des conclusions inexactes. Par exemple, les données sur les revenus qui excluent les revenus informels, comme les pourboires, peuvent sous-estimer les inégalités.
Il est également important de disposer d'un échantillon de taille suffisante pour obtenir une courbe plutôt qu'une ligne irrégulière, comme vous pouvez le voir dans la première figure. Comme toujours, il est important de veiller à ce que vos données soient aussi complètes que possible. Et, bien sûr, vous devez soigneusement valider vos données et documenter toutes les hypothèses formulées afin de garantir la transparence et la fiabilité.
La courbe de Lorenz ne rend pas non plus compte des inégalités multidimensionnelles. Elle se concentre sur une seule variable, telle que le revenu ou la richesse, et ne tient pas compte des effets combinés. Toutefois, si vous souhaitez mesurer l'inégalité multidimensionnelle, vous pouvez utiliser d'autres outils, tels que l'indice de pauvreté multidimensionnelle.
Avantages de la courbe de Lorenz
Le plus grand avantage de la courbe de Lorenz, à mon avis, est qu'elle fournit une représentation visuelle intuitive de l'inégalité, ce qui la rend facile à comprendre en un coup d'œil. En comparant la courbe à la ligne d'égalité parfaite, les disparités au sein d'une population apparaissent immédiatement. Il s'agit d'un outil de narration visuelle qui rend les données sur les inégalités accessibles aux publics techniques et non techniques.
Sa polyvalence est son autre atout majeur. La courbe de Lorenz peut être appliquée dans différents domaines, de l'économie à la santé publique en passant par l'écologie et l'apprentissage automatique. Cette flexibilité lui confère une grande utilité.
Conclusion
La courbe de Lorenz est un outil de narration polyvalent qui permet de montrer et de comprendre les inégalités. Si ce type de visualisation vous intéresse, vous pouvez consulter le site Geometric Mean : Une mesure de la croissance et de l'effet d'entraînement. Ou, si vous voulez en savoir plus sur la finance, je vous encourage à consulter notre cours Introduction à Python pour la finance et notre parcours de compétences Finance appliquée en Python.

Je suis titulaire d'un doctorat et j'ai 13 ans d'expérience dans le traitement des données dans un environnement de recherche biologique. Je crée des logiciels dans plusieurs langages de programmation, notamment Python, MATLAB et R. Je suis passionné par le partage de mon amour de l'apprentissage avec le monde.
FAQ
Qu'est-ce que la courbe de Lorenz ?
La courbe de Lorenz est un graphique montrant le degré d'inégalité d'une ressource au sein d'une population.
La courbe de Lorenz est-elle identique à l'indice de Gini ?
L'indice de Gini, ou coefficient de Gini, utilise la courbe de Lorenz pour son calcul. Mais il s'agit de mesures différentes.
Comment interpréter une courbe de Lorenz ?
D'une manière générale, plus la courbe s'éloigne de la ligne d'égalité, plus la distribution est inégale.
La courbe de Lorenz ne concerne-t-elle que les revenus ?
Bien qu'elle ait été développée à l'origine pour les revenus, la courbe de Lorenz peut être utilisée pour des données aussi disparates que les services de santé, la criminalité, la biodiversité et l'apprentissage automatique.
Quelle est la ligne d'égalité ?
La ligne d'égalité est une ligne droite diagonale qui représente l'égalité parfaite, c'est-à-dire que tout le monde dispose de la même quantité d'une ressource.
FAQ sur la courbe de Lorenz
Qu'est-ce que la courbe de Lorenz ?
La courbe de Lorenz est un graphique montrant le degré d'inégalité d'une ressource au sein d'une population.
La courbe de Lorenz est-elle identique à l'indice de Gini ?
L'indice de Gini, ou coefficient de Gini, utilise la courbe de Lorenz pour son calcul. Mais il s'agit de mesures différentes.
Comment interpréter une courbe de Lorenz ?
D'une manière générale, plus la courbe s'éloigne de la ligne d'égalité, plus la distribution est inégale.
La courbe de Lorenz ne concerne-t-elle que les revenus ?
Bien qu'elle ait été développée à l'origine pour les revenus, la courbe de Lorenz peut être utilisée pour des données aussi disparates que les services de santé, la criminalité, la biodiversité et l'apprentissage automatique.
Quelle est la ligne d'égalité ?
La ligne d'égalité est une ligne droite diagonale qui représente l'égalité parfaite, c'est-à-dire que tout le monde dispose de la même quantité d'une ressource.