Lernpfad
Ungleichheit ist ein Thema, das fast jeden Aspekt des Lebens betrifft: Einkommen, Vermögen, Gesundheit, Bildung und sogar die Verteilung von Ressourcen in Ökosystemen. Aber wie können wir das eigentlich messen? Eines der leistungsstärksten Instrumente zur Visualisierung von Ungleichheit ist die Lorenzkurve.
Obwohl die Lorenzkurve häufig zur Messung der Einkommensungleichheit verwendet wird, ist sie nicht nur für Ökonomen interessant. Im Laufe der Zeit hat sie sich zu einem vielseitigen Instrument entwickelt, das zur Untersuchung von Ungleichheiten im Gesundheitswesen, zur Erforschung der Artenvielfalt und sogar beim maschinellen Lernen zur Bewertung der Fairness von Vorhersagemodellen eingesetzt wird. Für Datenwissenschaftlerinnen und -wissenschaftler ist es eine tolle Möglichkeit, eine Geschichte über Ungleichheiten in einem Datensatz zu erzählen.
In diesem Lernprogramm zeige ich dir, wie die Lorenzkurve funktioniert. Wir besprechen, wie du sie mit deinem Datensatz in Python erstellst, und du lernst, wie du sie in deinen eigenen Projekten einsetzen kannst. Wenn du daran interessiert bist, die Einkommensungleichheit zu quantifizieren, die Kundensegmentierung zu analysieren oder die Ressourcenverteilung zu untersuchen, kann dir die Lorenzkurve helfen, diese komplexen Ideen mit einem einfachen Bild zu vermitteln.
Die Lorenzkurve verstehen
Die Lorenzkurve wurde 1905 von dem Ökonomen Max O. Lorenz eingeführt. Dabei wird die tatsächliche Verteilung einer Ressource mit einer hypothetischen Linie der vollkommenen Gleichheit verglichen (eine Linie, bei der jeder die gleiche Menge hat). Je weiter die Kurve von dieser perfekten Gleichheitslinie entfernt ist, desto größer ist die Ungleichheit in der Verteilung der jeweiligen Ressource.
Struktur der Lorenzkurve
Die Lorenzkurve hat eine einfache Struktur. Auf der x-Achse ist der kumulierte Anteil der Bevölkerung aufgetragen, beginnend mit dem ärmsten Individuum bis hin zum reichsten. Die y-Achse zeigt den kumulierten Anteil der gemessenen Ressource.
Als Nächstes müssen wir die Linie der vollkommenen Gleichheit hinzufügen. Das ist eine diagonale Linie, die von der linken unteren Ecke zur rechten oberen Ecke verläuft. Diese Linie stellt ein Szenario dar, in dem alle den gleichen Anteil an der Ressource haben, an der wir interessiert sind.
Die Lorenzkurve selbst zeigt die tatsächliche Verteilung der Ressource. Je weiter sich die Kurve von der Linie der perfekten Gleichheit entfernt, desto größer ist die Ungleichheit, die sie darstellt.
Wie man die Lorenzkurve interpretiert
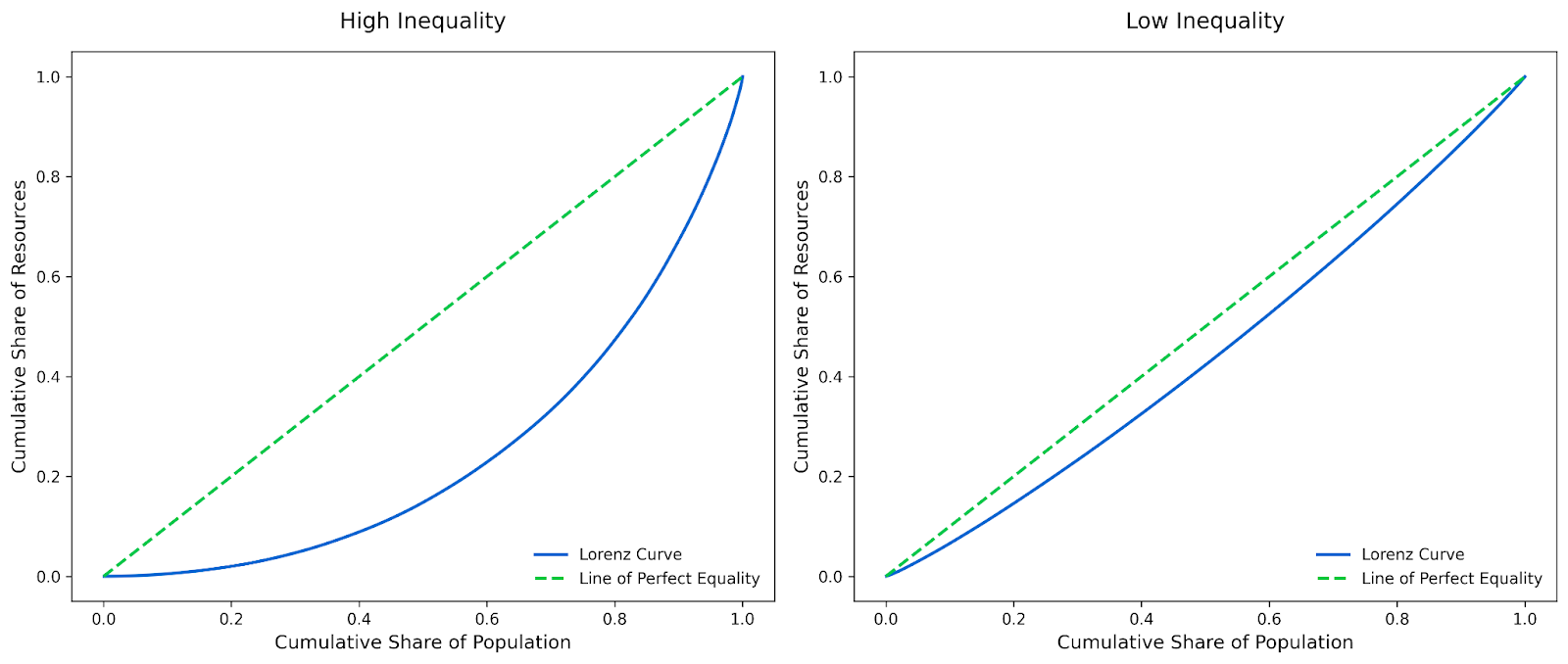
Wenn die Lorenzkurve nahe an der diagonalen Linie der perfekten Gleichheit liegt, bedeutet das, dass die Ressource ziemlich gleichmäßig verteilt ist. In einer Gesellschaft, in der die unteren 50 % der Bevölkerung etwa 50 % des Einkommens haben, liegt die Lorenzkurve beispielsweise näher an der Diagonale. Diese flache Kurve deutet auf eine geringe Ungleichheit hin.
Wenn sich die Kurve hingegen weit von der Diagonale wegwölbt, deutet dies auf eine hohe Ungleichheit hin. Das kann passieren, wenn z.B. die unteren 50% der Bevölkerung nur 10% des Einkommens haben, während die oberen 10% den ganzen Rest haben.
Wie man eine Lorenzkurve konstruiert
Lass uns gemeinsam die Lorenzkurve anhand eines einfachen Beispiels konstruieren. Stell dir vor, wir analysieren die Einkommensverteilung einer kleinen Bevölkerung.
Schritt 1: Sortiere die Daten
Der erste Schritt besteht darin, die Daten in aufsteigender Reihenfolge zu ordnen. Für dieses Beispiel nehmen wir an, dass wir die folgenden Einkommenswerte für fünf Personen in einer Population haben: $20, $30, $50, $80, $100.
Wir sortieren diese Werte vom kleinsten zum größten. So wird sichergestellt, dass die kumulierten Prozentsätze, die wir später berechnen, sinnvoll sind. Hier ist die sortierte Tabelle:
| Einzelne | Einkommen ($) |
|---|---|
| 1 | 120 |
| 2 | 230 |
| 3 | 350 |
| 4 | 480 |
| 5 | 5100 |
Schritt 2: Berechne kumulative Prozentsätze
Als Nächstes berechnen wir die kumulierten Prozentsätze sowohl für die Bevölkerung (x-Achse) als auch für das Einkommen (y-Achse).
- Für den kumulativen Bevölkerungsanteil teilst du die Position jeder Person in der sortierten Liste durch die Gesamtzahl der Personen. Das erste Individuum repräsentiert zum Beispiel 1/5 (oder 20%) der Bevölkerung, das zweite 2/5 (40%) und so weiter.
- Für den Prozentsatz des kumulierten Einkommens addierst du die Einkommen nach und nach und teilst jede kumulierte Summe durch die Gesamtsumme der Einkommen. In diesem Beispiel beläuft sich das Gesamteinkommen auf 280 US-Dollar. Das Einkommen der ersten Person (20 US-Dollar) entspricht also 20/280 (oder etwa 7,14 %), und die ersten beiden Personen zusammen entsprechen (20 + 30)/280 (etwa 17,86 %).
Hier ist die aktualisierte Tabelle mit den kumulierten Prozentsätzen:
| Einzelne | Einkommen ($) | Kumulative Bevölkerung (%) | Kumuliertes Einkommen (%) |
|---|---|---|---|
| 120 | 20 | 20% | 7.14% |
| 230 | 30 | 40% | 17.86% |
| 350 | 50 | 60% | 35.71% |
| 480 | 80 | 80% | 64.29% |
| 5100 | 100 | 100% | 100% |
Schritt 3: Zeichne die kumulative Verteilung
Jetzt, da wir die kumulierten Prozentsätze haben, können wir sie in ein Diagramm eintragen.
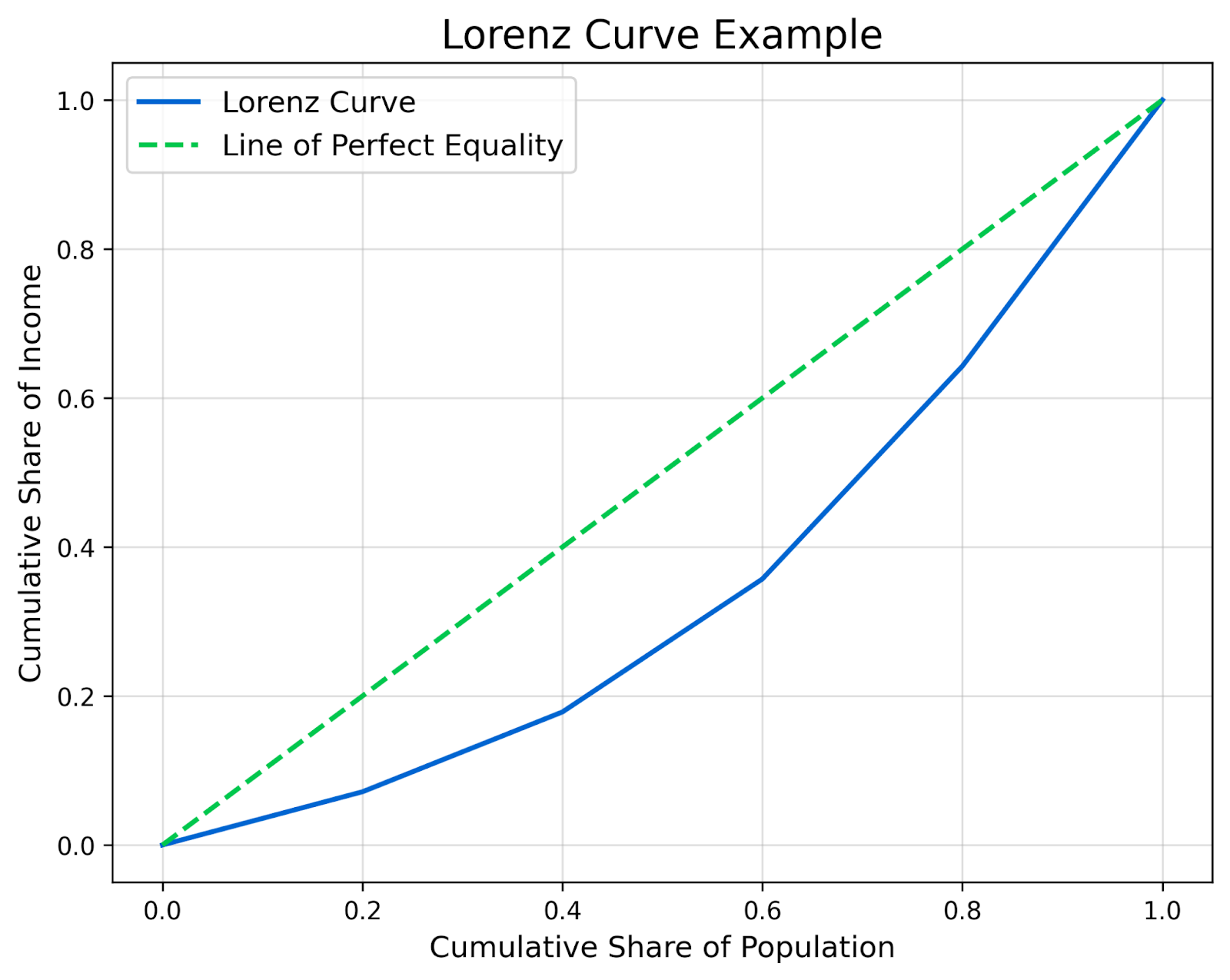
Die x-Achse stellt den kumulierten Anteil der Bevölkerung dar und die y-Achse den kumulierten Anteil des Einkommens. Jede Zeile in der Tabelle entspricht einem Punkt in der Grafik. Wenn die Punkte aufgezeichnet sind, verbinde sie, um die Lorenzkurve zu erstellen. Dann fügst du die Linie der vollkommenen Gleichheit hinzu.
Schritt 4: Interpretiere die Lorenzkurve
Die daraus resultierende Lorenzkurve zeigt die tatsächliche Einkommensverteilung in dieser Bevölkerung. Je weiter sich die Kurve von der Diagonale wegbiegt, desto größer ist die Ungleichheit. Wie du in diesem Beispiel sehen kannst, krümmt sich die Kurve merklich, weil die unteren 20% der Bevölkerung nur 7,14% des Einkommens besitzen.
Datenanforderungen und Herausforderungen
Um eine genaue Lorenzkurve zu erstellen, brauchst du hochwertige Daten, die ein paar wichtige Kriterien erfüllen. Die Qualität und Struktur deiner Daten wirkt sich direkt auf die Genauigkeit und Zuverlässigkeit deiner Ergebnisse aus.
Erstens ist die Stichprobengröße ein entscheidender Faktor. Kleine Datensätze können zu irreführenden Ergebnissen führen, da sie möglicherweise nicht das gesamte Spektrum der Ungleichheit in einer Bevölkerung erfassen. In unserem Beispiel wurde ein viel zu kleiner Datensatz von nur 5 Personen verwendet. Diese Kurve ist für ganze Populationen gedacht. Größere Datensätze liefern ein zuverlässigeres und repräsentativeres Bild der Ungleichheit, wodurch deine Lorenzkurve genauer wird.
Auch die Granularität ist wichtig, denn je detaillierter deine Daten sind, desto genauer wird deine Lorenzkurve sein. Das Einkommen von Einzelpersonen oder Haushalten gibt dir zum Beispiel einen besseren Eindruck von der Ungleichheit in einer Bevölkerung als das Einkommen ganzer Landkreise. Hinter letzterem Datensatz können sich viele Ungerechtigkeiten verbergen.
Wie bei den meisten Analysen sind unvollständige Daten ein häufiges Problem, das die Lorenzkurve erheblich verzerren kann. Fehlende Werte verursachen Lücken in den kumulierten Prozentsätzen, was zu ungenauen Ergebnissen führen kann. Bevor du deine Kurve konstruierst, solltest du sicherstellen, dass dein Datensatz so vollständig wie möglich ist, und sorgfältig überlegen, wie du mit fehlenden Daten umgehst. Wenn du dir nicht sicher bist, wie du mit fehlenden Daten umgehen sollst, schau dir unseren hilfreichen Kurs "Umgang mit fehlenden Daten in Python " an.
Praktisches Python Code Beispiel
Nachdem wir nun die Grundlagen kennen, wollen wir uns ansehen, wie die Lorenzkurve über die Einkommensdaten hinaus als Erzählinstrument genutzt werden kann.
In diesem Beispiel analysieren wir Kriminalitätsdaten, um die ungleiche Verteilung der gemeldeten Straftaten in den einzelnen Stadtteilen zu verstehen. Das wird zeigen, wie die Lorenzkurve auf Bereiche wie die öffentliche Politik angewendet werden kann.
Wir werden einen realen Datensatz aus der Verbrechensdatenbank des Chicago Police Departments verwenden, der online frei verfügbar ist. Du kannst den Datensatz vom Chicago Data Portal herunterladen. Dieser Datensatz enthält detaillierte Informationen über gemeldete Straftaten in Chicago, darunter die Art der Straftat, den Ort und das Datum.
Im Folgenden gehen wir die Schritte durch, um die Daten zu bereinigen, die Lorenzkurve zu berechnen und sie mit Python zu visualisieren. Wenn du neu in Python bist, empfehle ich dir unseren Kurs "Einführung in Python ", mit dem du die Sprache schnell erlernen kannst.
Installieren wir zunächst alle Bibliotheken, die wir für dieses Beispiel brauchen:
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltSchritt 1: Herunterladen und Laden des Datensatzes
Der folgende Code soll den Datensatz vom Chicago Data Portal als CSV-Datei herunterladen und mit Pandas in Python laden.
# Load the dataset
url = "<https://data.cityofchicago.org/resource/ijzp-q8t2.csv?$limit=100000>" # Limit to 100,000 rows for simplicity
data = pd.read_csv(url)Schritt 2: Aggregierte Kriminalitätsdaten nach Stadtteilen
Dieser Datensatz enthält eine Spalte für Gemeindegebiete oder Nachbarschaften. Wir werden die Daten nach dieser Spalte gruppieren, um die Gesamtzahl der gemeldeten Straftaten in den einzelnen Stadtteilen zu berechnen.
# Group by community area and count the number of crimes
crime_counts = data.groupby("community_area").size().reset_index(name="crime_count")
# Drop rows with missing community area values
crime_counts = crime_counts.dropna()
# Sort by crime count
crime_counts = crime_counts.sort_values(by="crime_count").reset_index(drop=True)
# Display the aggregated data
print(crime_counts.head())Output:
community_area crime_count
0 47.0 102
1 9.0 102
2 12.0 195
3 74.0 212
4 37.0 246Schritt 3: Berechne kumulative Prozentsätze
Um die Lorenzkurve zu erstellen, müssen wir den kumulativen Prozentsatz der Stadtteile und den kumulativen Prozentsatz der Straftaten berechnen.
# Calculate cumulative percentages
crime_counts["cumulative_crime"] = crime_counts["crime_count"].cumsum()
crime_counts["cumulative_crime_percentage"] = crime_counts["cumulative_crime"] / crime_counts["crime_count"].sum()
crime_counts["cumulative_population_percentage"] = (np.arange(1, len(crime_counts) + 1)) / len(crime_counts)
# Display the updated data
print(crime_counts.head())Output:
community_area crime_count cumulative_crime cumulative_crime_percentage \\
0 47.0 102 102 0.00102
1 9.0 102 204 0.00204
2 12.0 195 399 0.00399
3 74.0 212 611 0.00611
4 37.0 246 857 0.00857
cumulative_population_percentage
0 0.012987
1 0.025974
2 0.038961
3 0.051948
4 0.064935 Schritt 4: Zeichne die Lorenzkurve
Jetzt, da wir die kumulierten Prozentsätze haben, können wir die Lorenzkurve aufzeichnen. Die x-Achse stellt den kumulierten Anteil der Stadtteile dar und die y-Achse den kumulierten Anteil der Straftaten. Um ein regionales Flair zu schaffen, werden wir die Farben der Chicago Bears als Inspiration für unseren Plot verwenden.
# Example data for cumulative percentages
# x represents the cumulative share of neighborhoods
# y represents the cumulative share of crimes
x = np.linspace(0, 1, 100) # Replace with actual data
y = x**2 # Replace with actual data
# Chicago Bears-inspired colors
blue = "#0065D1" # Lighter blue for the Lorenz curve
orange = "#FF5A1F" # Bright orange for the line of perfect equality
# Create the plot
plt.figure(figsize=(8, 6))
# Plot the Lorenz curve
# This curve shows the inequality in crime distribution across neighborhoods
plt.plot(x, y, label="Lorenz Curve", color=blue, linewidth=2)
# Plot the line of perfect equality
# This line represents a hypothetical scenario where crimes are evenly distributed
plt.plot([0, 1], [0, 1], label="Line of Perfect Equality", color=orange, linestyle="--", linewidth=2)
# Add a title to explain what the graph represents
plt.title("Lorenz Curve of Crime Distribution Across Chicago Neighborhoods", fontsize=16, color="black", pad=15)
# Label the x-axis to show what the horizontal axis represents
plt.xlabel("Cumulative Share of Neighborhoods", fontsize=12, color="black", labelpad=10)
# Label the y-axis to show what the vertical axis represents
plt.ylabel("Cumulative Share of Crimes", fontsize=12, color="black", labelpad=10)
# Add a legend to explain the two lines
plt.legend(fontsize=12, loc="lower right", frameon=False)
# Remove the grid for a cleaner look
plt.grid(False)
# Set the background color to white for a professional appearance
plt.gca().set_facecolor("white")
# Remove the top and right borders of the graph for a minimalist design
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
# Save the plot as a PNG file
# This saves the graph as an image file for sharing or embedding in reports
plt.savefig("lorenz_curve_crime.png", dpi=300, bbox_inches="tight")
# Display the plot
plt.show()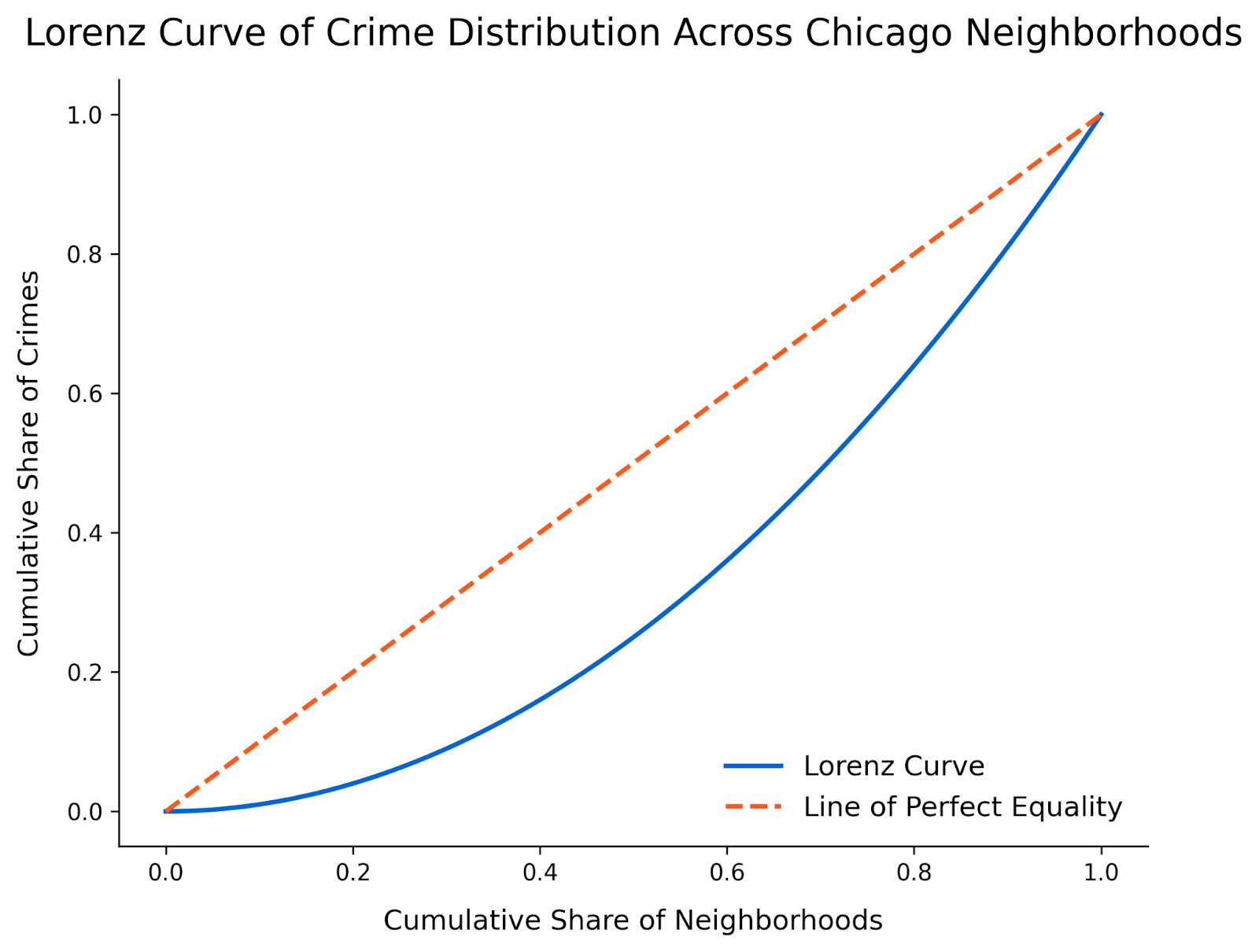
Schritt 5: Interpretiere die Ergebnisse
Schließlich müssen wir das Diagramm interpretieren. Diese Lorenzkurve zeigt eine auffällige Ungleichheit in der Verteilung der Straftaten in den Chicagoer Stadtvierteln. Die Kurve weicht deutlich von der Linie der perfekten Gleichheit ab, was zeigt, dass ein kleiner Teil der Stadtteile für die Mehrheit der gemeldeten Straftaten verantwortlich ist.
Es sieht so aus, als ob die ersten 50 % der Stadtteile zu weniger als 20 % der Gesamtkriminalität beitragen, während die übrigen Stadtteile den Großteil der Kriminalitätslast tragen. Diese Visualisierung hebt Muster der Ungleichheit hervor, die in anderen Arten von Diagrammen vielleicht nicht so offensichtlich sind. Der nächste Schritt kann darin bestehen, Stadtteile mit höherer Kriminalität zu identifizieren, um Maßnahmen zur Eindämmung zu ergreifen, oder Stadtteile mit geringerer Kriminalität zu identifizieren, um zu sehen, welche Abschreckungsmaßnahmen funktionieren.
Dieses Beispiel zeigt, wie die Lorenzkurve über Einkommensdaten hinaus angewendet werden kann, um überzeugende Geschichten über Ungleichheit in anderen Bereichen zu erzählen. Durch die Analyse von Kriminalitätsdaten können wir Muster der Ungleichheit aufdecken, die uns bei politischen und stadtplanerischen Entscheidungen helfen. Versuche, diese Methode auf andere Datensätze anzuwenden, z. B. auf den Zugang zur Gesundheitsversorgung, Bildungsergebnisse oder Umweltdaten, um Ungleichheit auf neue und sinnvolle Weise zu untersuchen.
Die Lorenzkurve vs. der Gini-Koeffizient
Der Gini-Koeffizient wird direkt von der Lorenzkurve abgeleitet. Sie misst die Fläche zwischen der Lorenzkurve und der Linie der vollkommenen Gleichheit. Ein größerer Bereich zeigt eine größere Ungleichheit an, während ein kleinerer Bereich auf mehr Gleichheit hindeutet. Der Gini-Koeffizient reicht von 0 bis 1, wobei 0 für perfekte Gleichheit steht (alle haben die gleichen Ressourcen) und 1 für extreme Ungleichheit (eine Person besitzt alle Ressourcen).
Welche Maßnahme du verwendest, hängt von deinen Zielen ab. Die Lorenzkurve zeigt die Form der Ungleichheit, während der Gini-Koeffizient eine numerische Zusammenfassung davon liefert. Wenn du das Ausmaß der Ungleichheit innerhalb einer Population untersuchen willst, bietet die Lorenzkurve mehr Details. Wenn du jedoch viele Populationen miteinander vergleichst, kann es mühsam sein, die Lorenzkurven der einzelnen Populationen zu vergleichen, daher ist der Gini-Koeffizient vielleicht besser geeignet. Wenn du tiefer in den Gini-Koeffizienten eintauchen möchtest, schau dir mein Tutorial zum Verständnis des Gini-Koeffizienten an.
Außerdem ist die Lorenzkurve vielleicht flexibler, da sie auf verschiedene Arten von Daten angewendet werden kann, z. B. auf Einkommen, Kriminalität, Zugang zur Gesundheitsversorgung oder Biodiversität, und zum Vergleich von Verteilungen im Laufe der Zeit oder zwischen Gruppen verwendet werden kann. Der Gini-Koeffizient kann auch für diese Art von Vergleichen verwendet werden, aber er hat den Ruf, hauptsächlich zur Messung der Einkommensungleichheit verwendet zu werden. Dies kann für einige Verbraucher zu einer Verzerrung führen. Meiner Erfahrung nach neigen Menschen dazu, bei der Interpretation von Diagrammen weniger voreingenommen zu sein, als wenn sie eine Zahl vorgesetzt bekommen.
| Feature | Lorenzkurve | Gini-Koeffizient |
|---|---|---|
| Zweck | Zeigt die Verteilung der Ressourcen in einer Bevölkerung | Fasst die Ungleichheit zu einem einzigen Wert zusammen |
| Typ | Visuelle Darstellung | Numerische Darstellung |
| Interpretation | Die Form der Kurve zeigt den Grad der Ungleichheit an | Der Wert reicht von 0 (perfekte Gleichheit) bis 1 (extreme Ungleichheit) |
| Anwendungsfälle | Verteilungen vergleichen, Muster erkennen und Ergebnisse kommunizieren | Vergleich von Ungleichheitsniveaus zwischen Datensätzen oder Populationen |
| Flexibilität | Kann auf verschiedene Datensätze angewendet werden (z. B. Einkommen, Kriminalität, Biodiversität) | Hauptsächlich für Einkommens- oder Vermögensungleichheit verwendet |
| Handlungsfähigkeit | Hilft dabei, bestimmte Bereiche der Ungleichheit für gezielte Interventionen zu identifizieren | Bietet eine übersichtliche Zusammenfassung für umfassende Vergleiche |
Der obige Vergleich verdeutlicht, wie sich die Lorenzkurve und der Gini-Koeffizient gegenseitig ergänzen. Die Lorenzkurve bietet eine detailliertere und visuelle Perspektive für eine Population, während der Gini-Koeffizient eine prägnante Zusammenfassung liefert, die zum Vergleich zwischen Populationen verwendet werden kann.
Anwendungen der Lorenzkurve in der realen Welt
Die Lorenzkurve ist ein vielseitiges Instrument, das in einer Vielzahl von Bereichen eingesetzt wird. Sehen wir uns ein paar seiner wirkungsvollsten Anwendungen an.
- Die Lorenzkurve in Wirtschaft und Finanzen: Die Lorenzkurve wird vor allem zur Analyse der Einkommens- und Vermögensungleichheit verwendet. Wirtschaftswissenschaftler und politische Entscheidungsträger verlassen sich darauf, um zu verstehen, wie die Ressourcen innerhalb einer Bevölkerung verteilt sind und um Maßnahmen wie Steuerpolitik oder Sozialprogramme zu entwerfen.
- Die Lorenzkurve in der öffentlichen Gesundheit und Epidemiologie: Im öffentlichen Gesundheitswesen kann die Lorenzkurve verwendet werden, um Ungleichheiten bei den Gesundheitsergebnissen oder beim Zugang zur Gesundheitsversorgung zu messen. Dies hilft Forschern und politischen Entscheidungsträgern, Ungleichheiten zu erkennen und Ressourcen effektiver zu verteilen.
- Die Lorenzkurve in Ökologie und Biodiversität: Ökologen können die Lorenzkurve nutzen, um die Verteilung und Häufigkeit von Arten zu untersuchen. Sie kann helfen, die Artenvielfalt zu quantifizieren und Ökosysteme zu identifizieren, in denen einige wenige Arten dominieren, während andere selten sind.
- Die Lorenzkurve in der Datenwissenschaft und im maschinellen Lernen: Die Lorenzkurve wird in der Datenwissenschaft immer häufiger verwendet, um Verteilungen zu analysieren und die Fairness von Vorhersagemodellen zu bewerten. Ein Beispiel dafür ist die Kundenanalyse. Unternehmen können die Lorenzkurve nutzen, um die Umsatzkonzentration unter den Kunden zu verstehen. Es kann dabei helfen, herauszufinden, welche Nutzerinnen und Nutzer den größten Teil des Umsatzes erzielen, was wiederum die Grundlage für Marketingstrategien oder Treueprogramme bilden kann.
- Die Lorenzkurve in der Datenwissenschaft und im maschinellen Lernen: Ein weiteres Beispiel, das mich überrascht hat, ist das maschinelle Lernen. Die Lorenzkurve kann Datenwissenschaftlern helfen zu beurteilen, ob die Vorhersagen eines Modells verzerrt sind. Bei einem Modell zur Kreditvergabe könnte die Kurve zum Beispiel zeigen, dass eine kleine Gruppe von Antragstellern die meisten Genehmigungen erhält, was auf eine mögliche Verzerrung im Algorithmus hinweist.
Vorteile und Grenzen der Lorenzkurve
Wie jede Methode hat auch die Lorenzkurve ihre Stärken und Schwächen.
Grenzen der Lorenzkurve
Die Lorenz-Kurve erfordert oft sehr detaillierte Daten, um aussagekräftige Ergebnisse zu erzielen. Aggregierte oder unvollständige Datensätze können manchmal zu ungenauen Schlussfolgerungen führen. Zum Beispiel können Einkommensdaten, die informelle Einkünfte wie Trinkgelder nicht berücksichtigen, die Ungleichheit unterschätzen.
Es ist auch wichtig, dass die Stichprobe groß genug ist, um eine Kurve statt einer gezackten Linie zu erhalten, wie du in der ersten Abbildung sehen kannst. Wie immer ist es wichtig, dass deine Daten so vollständig wie möglich sind. Und natürlich solltest du deine Daten sorgfältig validieren und alle getroffenen Annahmen dokumentieren, um Transparenz und Zuverlässigkeit zu gewährleisten.
Die Lorenzkurve erfasst auch nicht die mehrdimensionale Ungleichheit. Sie konzentriert sich auf eine einzelne Variable, wie Einkommen oder Vermögen, und berücksichtigt keine kombinierten Effekte. Wenn du jedoch die mehrdimensionale Ungleichheit messen willst, gibt es andere Instrumente, die du verwenden kannst, wie zum Beispiel den Multidimensionalen Armutsindex.
Vorteile der Lorenzkurve
Der größte Vorteil der Lorenz-Kurve ist meiner Meinung nach, dass sie eine intuitive visuelle Darstellung der Ungleichheit bietet, die auf den ersten Blick leicht zu verstehen ist. Wenn du die Kurve mit der Linie der perfekten Gleichheit vergleichst, werden Ungleichheiten innerhalb einer Bevölkerung sofort sichtbar. Es ist ein visuelles Storytelling-Tool, das Ungleichheitsdaten sowohl einem technischen als auch einem nicht-technischen Publikum zugänglich macht.
Seine Vielseitigkeit ist ein weiterer großer Vorteil. Die Lorenzkurve kann in verschiedenen Bereichen angewendet werden, von der Wirtschaft und dem Gesundheitswesen bis hin zur Ökologie und dem maschinellen Lernen. Diese Flexibilität macht sie sehr nützlich.
Fazit
Die Lorenzkurve ist ein vielseitiges Erzählinstrument, das nützlich ist, um Ungleichheit darzustellen und zu verstehen. Wenn du dich für diese Art der Visualisierung interessierst, könnte dir die Seite Geometrisches Mittel gefallen: Ein Maß für Wachstum und Compounding. Wenn du mehr über Finanzen lernen möchtest, empfehle ich dir unseren Kurs Einführung in Python für Finanzen und unseren Lernpfad Angewandte Finanzwissenschaft in Python.

Ich bin promoviert und habe 13 Jahre Erfahrung in der Arbeit mit Daten in der biologischen Forschung. Ich entwickle Software in verschiedenen Programmiersprachen, darunter Python, MATLAB und R. Meine Leidenschaft ist es, meine Liebe zum Lernen mit der Welt zu teilen.
FAQs
Was ist die Lorenzkurve?
Die Lorenzkurve ist eine Grafik, die das Ausmaß der Ungleichheit einer Ressource in einer Bevölkerung zeigt.
Ist die Lorenzkurve dasselbe wie der Gini-Index?
Der Gini-Index oder Gini-Koeffizient wird anhand der Lorenzkurve berechnet. Aber es sind unterschiedliche Messgrößen.
Wie interpretierst du eine Lorenzkurve?
Generell gilt: Je weiter die Kurve von der Gleichheitslinie entfernt ist, desto ungleicher ist die Verteilung.
Gilt die Lorenzkurve nur für das Einkommen?
Ursprünglich wurde sie für das Einkommen entwickelt, aber die Lorenzkurve kann auch für so unterschiedliche Daten wie Gesundheitsdienste, Kriminalität, Biodiversität und maschinelles Lernen verwendet werden.
Was ist die Grenze der Gleichheit?
Die Gleichheitslinie ist eine gerade, diagonale Linie, die perfekte Gleichheit darstellt, d.h. jeder hat die gleiche Menge einer Ressource.
FAQs zur Lorenzkurve
Was ist die Lorenzkurve?
Die Lorenzkurve ist eine Grafik, die das Ausmaß der Ungleichheit einer Ressource in einer Bevölkerung zeigt.
Ist die Lorenzkurve dasselbe wie der Gini-Index?
Der Gini-Index oder Gini-Koeffizient nutzt die Lorenz-Kurve für seine Berechnung. Aber es sind unterschiedliche Messgrößen.
Wie interpretierst du eine Lorenzkurve?
Generell gilt: Je weiter die Kurve von der Gleichheitslinie entfernt ist, desto ungleicher ist die Verteilung.
Gilt die Lorenzkurve nur für das Einkommen?
Ursprünglich wurde sie für das Einkommen entwickelt, aber die Lorenzkurve kann auch für so unterschiedliche Daten wie Gesundheitsdienste, Kriminalität, Biodiversität und maschinelles Lernen verwendet werden.
Was ist die Grenze der Gleichheit?
Die Gleichheitslinie ist eine gerade, diagonale Linie, die perfekte Gleichheit darstellt, d.h. jeder hat die gleiche Menge einer Ressource.
