Programa
A desigualdade é um tópico que afeta quase todos os aspectos da vida: renda, riqueza, saúde, educação e até mesmo como os recursos são distribuídos nos ecossistemas. Mas como podemos realmente medir isso? Uma das ferramentas mais poderosas que encontrei para visualizar a desigualdade é a curva de Lorenz.
Embora seja comumente usada para medir a desigualdade de renda, a curva de Lorenz não é apenas para economistas. Com o tempo, ela se tornou uma ferramenta versátil usada para examinar as disparidades na área da saúde, estudar a biodiversidade e até mesmo no machine learning para avaliar a justiça em modelos preditivos. Para os cientistas de dados, essa é uma ótima maneira de contar uma história sobre a desigualdade em um conjunto de dados.
Neste tutorial, mostrarei a você como funciona a curva de Lorenz. Discutiremos como criá-lo com seu conjunto de dados, usando Python, e você aprenderá a usá-lo em seus próprios projetos. Se você estiver interessado em quantificar a desigualdade de renda, analisar a segmentação de clientes ou investigar a alocação de recursos, a curva de Lorenz pode ajudá-lo a comunicar essas ideias complexas com um visual simples.
Entendendo a curva de Lorenz
A curva de Lorenz foi introduzida em 1905 pelo economista Max O. Lorenz. A maneira como funciona é comparando a distribuição real de um recurso com uma linha hipotética de igualdade perfeita (uma linha em que todos têm uma quantidade igual). Quanto mais distante a curva estiver dessa linha de igualdade perfeita, maior será a desigualdade na distribuição desse recurso específico.
Estrutura da curva de Lorenz
A curva de Lorenz tem uma estrutura simples. Em seu eixo x, plotamos a participação cumulativa da população, começando com o indivíduo mais pobre e indo até o mais rico. O eixo y mostra a participação cumulativa do recurso que está sendo medido.
Em seguida, precisamos adicionar a linha de igualdade perfeita, que é uma linha diagonal que vai do canto inferior esquerdo ao canto superior direito. Essa linha representa um cenário em que todos têm uma parcela igual do recurso no qual estamos interessados.
A própria curva de Lorenz mostra a distribuição real do recurso. Quanto mais a curva se afasta da linha de igualdade perfeita, maior é a desigualdade que ela representa.
Como interpretar a curva de Lorenz
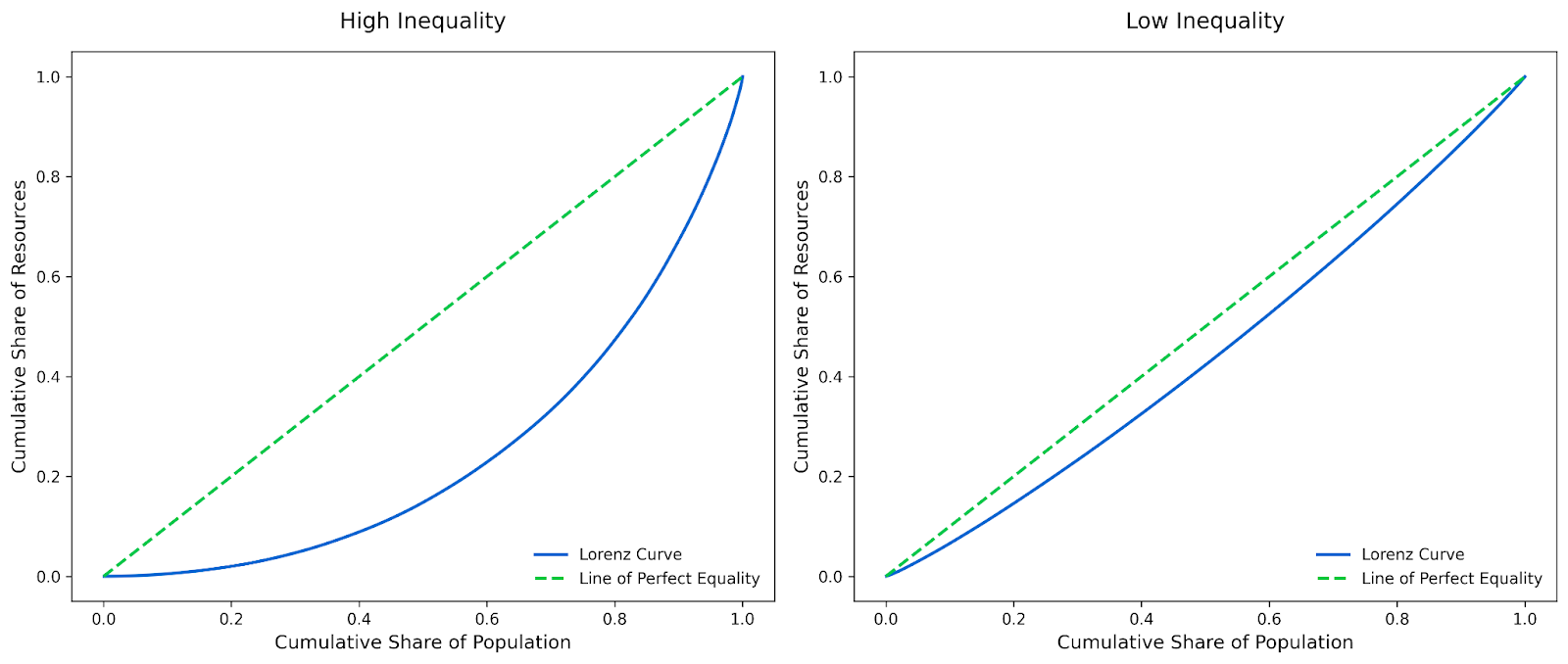
Se a curva de Lorenz estiver próxima da linha diagonal de igualdade perfeita, isso significa que o recurso é distribuído de forma bastante uniforme. Por exemplo, em uma sociedade em que os 50% inferiores da população têm aproximadamente 50% da renda, a curva de Lorenz estaria mais próxima da diagonal. Essa curva rasa indica baixa desigualdade.
Por outro lado, se a curva se inclinar para longe da diagonal, isso indica alta desigualdade. Isso pode acontecer se, por exemplo, os 50% inferiores da população tiverem apenas 10% da renda, enquanto os 10% superiores tiverem todo o restante.
Como construir uma curva de Lorenz
Vamos analisar a construção de uma curva de Lorenz juntos, usando um exemplo simples. Imagine que estamos analisando a distribuição de renda de uma pequena população.
Etapa 1: Classificar os dados
A primeira etapa é organizar os dados em ordem crescente. Para este exemplo, digamos que você tenha os seguintes valores de renda para cinco indivíduos em uma população: $20, $30, $50, $80, $100.
Classificaremos esses valores do menor para o maior. Isso garante que as porcentagens cumulativas que calculamos posteriormente façam sentido. Aqui está a tabela classificada:
| Individual | Renda ($) |
|---|---|
| 1 | 120 |
| 2 | 230 |
| 3 | 350 |
| 4 | 480 |
| 5 | 5100 |
Etapa 2: Calcular porcentagens cumulativas
Em seguida, calculamos as porcentagens acumuladas para a população (eixo x) e a renda (eixo y).
- Para obter a porcentagem da população cumulativa, divida a posição de cada indivíduo na lista ordenada pelo número total de indivíduos. Por exemplo, o primeiro indivíduo representa 1/5 (ou 20%) da população, o segundo representa 2/5 (40%) e assim por diante.
- Para obter a porcentagem de renda acumulada, some as rendas progressivamente e divida cada total acumulado pelo total geral de renda. Neste exemplo, a renda total é de US$ 280, portanto, a renda do primeiro indivíduo (US$ 20) representa 20/280 (ou aproximadamente 7,14%), e os dois primeiros indivíduos juntos representam (20 + 30)/280 (aproximadamente 17,86%).
Aqui está a tabela atualizada com as porcentagens cumulativas:
| Individual | Renda ($) | População cumulativa (%) | Renda acumulada (%) |
|---|---|---|---|
| 120 | 20 | 20% | 7.14% |
| 230 | 30 | 40% | 17.86% |
| 350 | 50 | 60% | 35.71% |
| 480 | 80 | 80% | 64.29% |
| 5100 | 100 | 100% | 100% |
Etapa 3: Trace a distribuição cumulativa
Agora que temos as porcentagens cumulativas, podemos plotá-las em um gráfico.
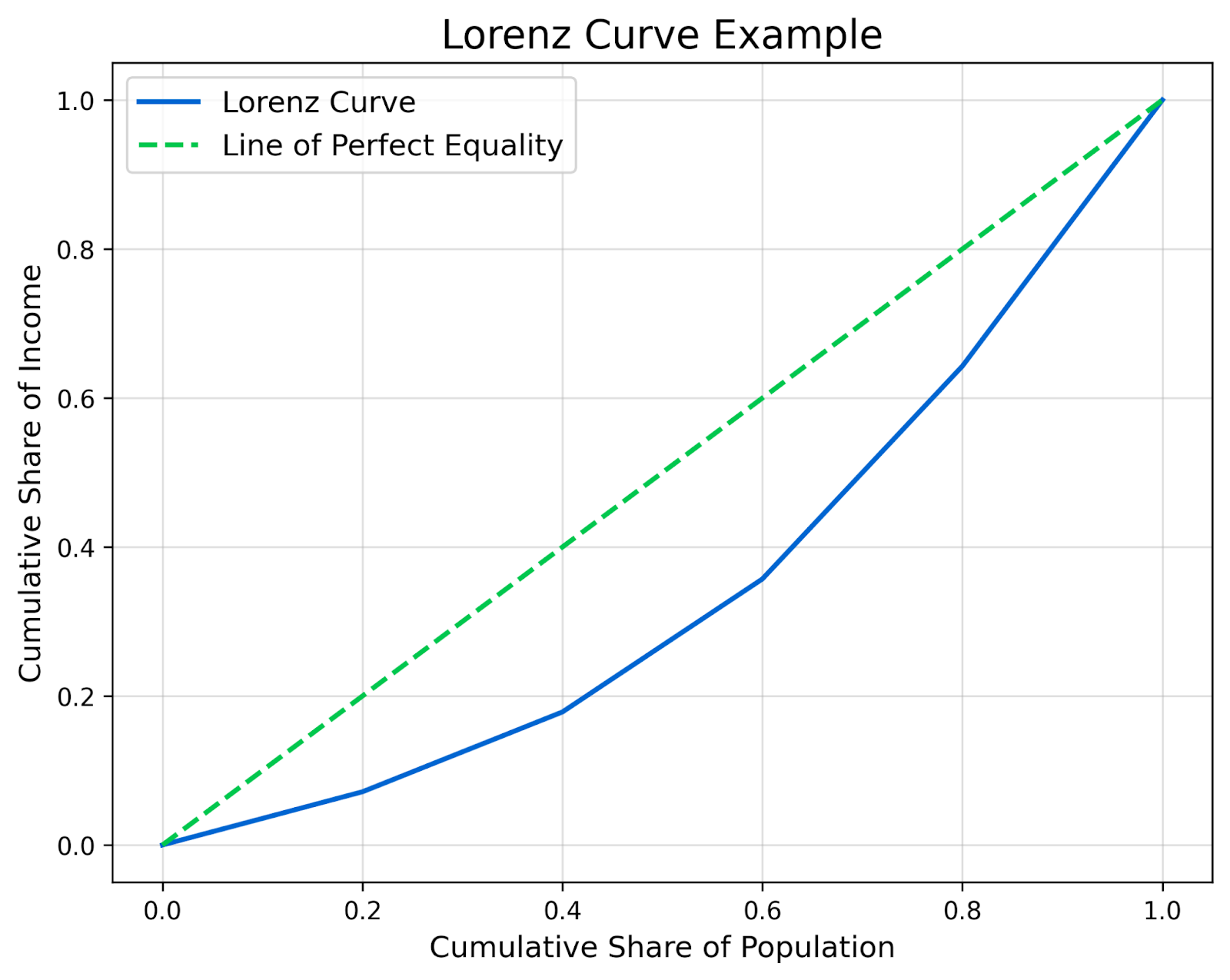
O eixo x representa a parcela cumulativa da população, e o eixo y representa a parcela cumulativa da renda. Cada linha da tabela corresponde a um ponto no gráfico. Depois que os pontos forem plotados, conecte-os para formar a curva de Lorenz. Em seguida, adicione a linha de igualdade perfeita.
Etapa 4: Interpretar a curva de Lorenz
A curva de Lorenz resultante mostra a distribuição real da renda nessa população. Quanto mais a curva se afasta da linha diagonal, maior é a desigualdade. Como você pode ver neste exemplo, a curva se inclina visivelmente porque os 20% inferiores da população detêm apenas 7,14% da renda.
Requisitos de dados e desafios
Para construir uma curva de Lorenz precisa, você precisará de dados de alta qualidade que atendam a alguns critérios importantes. A qualidade e a estrutura dos seus dados afetarão diretamente a precisão e a confiabilidade dos seus resultados.
Em primeiro lugar, o tamanho da amostra é um fator crítico. Conjuntos de dados pequenos podem levar a resultados enganosos, pois podem não captar toda a gama de desigualdade em uma população. Nosso exemplo aqui usou um conjunto de dados muito pequeno, com apenas 5 indivíduos. Essa curva foi projetada para populações inteiras. Conjuntos de dados maiores fornecem uma imagem mais confiável e representativa da desigualdade, tornando sua curva de Lorenz mais precisa.
A granularidade também é importante porque, quanto mais detalhados forem os dados, mais precisa será a curva de Lorenz. Por exemplo, a renda de indivíduos ou famílias dará a você uma ideia melhor da desigualdade em uma população do que a renda de municípios inteiros. Esse último conjunto de dados pode ocultar muitas desigualdades.
Como na maioria das análises, dados incompletos são um problema comum que pode distorcer significativamente a curva de Lorenz. Os valores ausentes criam lacunas nas porcentagens cumulativas, o que pode levar a resultados imprecisos. Antes de construir sua curva, certifique-se de que o conjunto de dados seja o mais completo possível e considere cuidadosamente como você lidará com os dados ausentes. Se você não tiver certeza de como lidar com dados ausentes, confira nosso curso muito útil Dealing with Missing Data in Python.
Exemplo prático de código Python
Agora que você já entendeu o básico, vamos explorar como a curva de Lorenz pode ser usada como uma ferramenta para contar histórias além dos dados de renda.
Neste exemplo, analisaremos dados de crimes para entender a desigualdade na distribuição de crimes relatados entre os bairros de uma cidade. Isso demonstrará como a curva de Lorenz pode ser aplicada a campos como políticas públicas.
Usaremos um conjunto de dados do mundo real do banco de dados de crimes do Departamento de Polícia de Chicago, que está disponível gratuitamente on-line. Você pode fazer o download do conjunto de dados no Chicago Data Portal. Esse conjunto de dados contém informações detalhadas sobre crimes denunciados em Chicago, incluindo o tipo de crime, o local e a data.
A seguir, você verá as etapas para limpar os dados, calcular a curva de Lorenz e visualizá-la usando Python. Se você é novo no Python, recomendo nosso curso Introduction to Python como uma maneira rápida de aprender a linguagem.
Primeiro, vamos instalar todas as bibliotecas necessárias para este exemplo:
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltEtapa 1: Faça o download e carregue o conjunto de dados
O código abaixo deve baixar o conjunto de dados do Chicago Data Portal como um arquivo CSV e carregá-lo no Python usando o pandas.
# Load the dataset
url = "<https://data.cityofchicago.org/resource/ijzp-q8t2.csv?$limit=100000>" # Limit to 100,000 rows for simplicity
data = pd.read_csv(url)Etapa 2: Dados agregados sobre crimes por bairro
Esse conjunto de dados contém uma coluna para áreas comunitárias, ou bairros. Agruparemos os dados por essa coluna para calcular o número total de crimes registrados em cada bairro.
# Group by community area and count the number of crimes
crime_counts = data.groupby("community_area").size().reset_index(name="crime_count")
# Drop rows with missing community area values
crime_counts = crime_counts.dropna()
# Sort by crime count
crime_counts = crime_counts.sort_values(by="crime_count").reset_index(drop=True)
# Display the aggregated data
print(crime_counts.head())Output:
community_area crime_count
0 47.0 102
1 9.0 102
2 12.0 195
3 74.0 212
4 37.0 246Etapa 3: Calcular porcentagens cumulativas
Para construir a curva de Lorenz, precisamos calcular a porcentagem cumulativa de bairros e a porcentagem cumulativa de crimes.
# Calculate cumulative percentages
crime_counts["cumulative_crime"] = crime_counts["crime_count"].cumsum()
crime_counts["cumulative_crime_percentage"] = crime_counts["cumulative_crime"] / crime_counts["crime_count"].sum()
crime_counts["cumulative_population_percentage"] = (np.arange(1, len(crime_counts) + 1)) / len(crime_counts)
# Display the updated data
print(crime_counts.head())Output:
community_area crime_count cumulative_crime cumulative_crime_percentage \\
0 47.0 102 102 0.00102
1 9.0 102 204 0.00204
2 12.0 195 399 0.00399
3 74.0 212 611 0.00611
4 37.0 246 857 0.00857
cumulative_population_percentage
0 0.012987
1 0.025974
2 0.038961
3 0.051948
4 0.064935 Etapa 4: Trace a curva de Lorenz
Agora que temos as porcentagens cumulativas, podemos traçar a curva de Lorenz. O eixo x representa a parcela cumulativa de bairros e o eixo y representa a parcela cumulativa de crimes. Para dar um toque regional, usaremos as cores do Chicago Bears como inspiração para nosso enredo.
# Example data for cumulative percentages
# x represents the cumulative share of neighborhoods
# y represents the cumulative share of crimes
x = np.linspace(0, 1, 100) # Replace with actual data
y = x**2 # Replace with actual data
# Chicago Bears-inspired colors
blue = "#0065D1" # Lighter blue for the Lorenz curve
orange = "#FF5A1F" # Bright orange for the line of perfect equality
# Create the plot
plt.figure(figsize=(8, 6))
# Plot the Lorenz curve
# This curve shows the inequality in crime distribution across neighborhoods
plt.plot(x, y, label="Lorenz Curve", color=blue, linewidth=2)
# Plot the line of perfect equality
# This line represents a hypothetical scenario where crimes are evenly distributed
plt.plot([0, 1], [0, 1], label="Line of Perfect Equality", color=orange, linestyle="--", linewidth=2)
# Add a title to explain what the graph represents
plt.title("Lorenz Curve of Crime Distribution Across Chicago Neighborhoods", fontsize=16, color="black", pad=15)
# Label the x-axis to show what the horizontal axis represents
plt.xlabel("Cumulative Share of Neighborhoods", fontsize=12, color="black", labelpad=10)
# Label the y-axis to show what the vertical axis represents
plt.ylabel("Cumulative Share of Crimes", fontsize=12, color="black", labelpad=10)
# Add a legend to explain the two lines
plt.legend(fontsize=12, loc="lower right", frameon=False)
# Remove the grid for a cleaner look
plt.grid(False)
# Set the background color to white for a professional appearance
plt.gca().set_facecolor("white")
# Remove the top and right borders of the graph for a minimalist design
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
# Save the plot as a PNG file
# This saves the graph as an image file for sharing or embedding in reports
plt.savefig("lorenz_curve_crime.png", dpi=300, bbox_inches="tight")
# Display the plot
plt.show()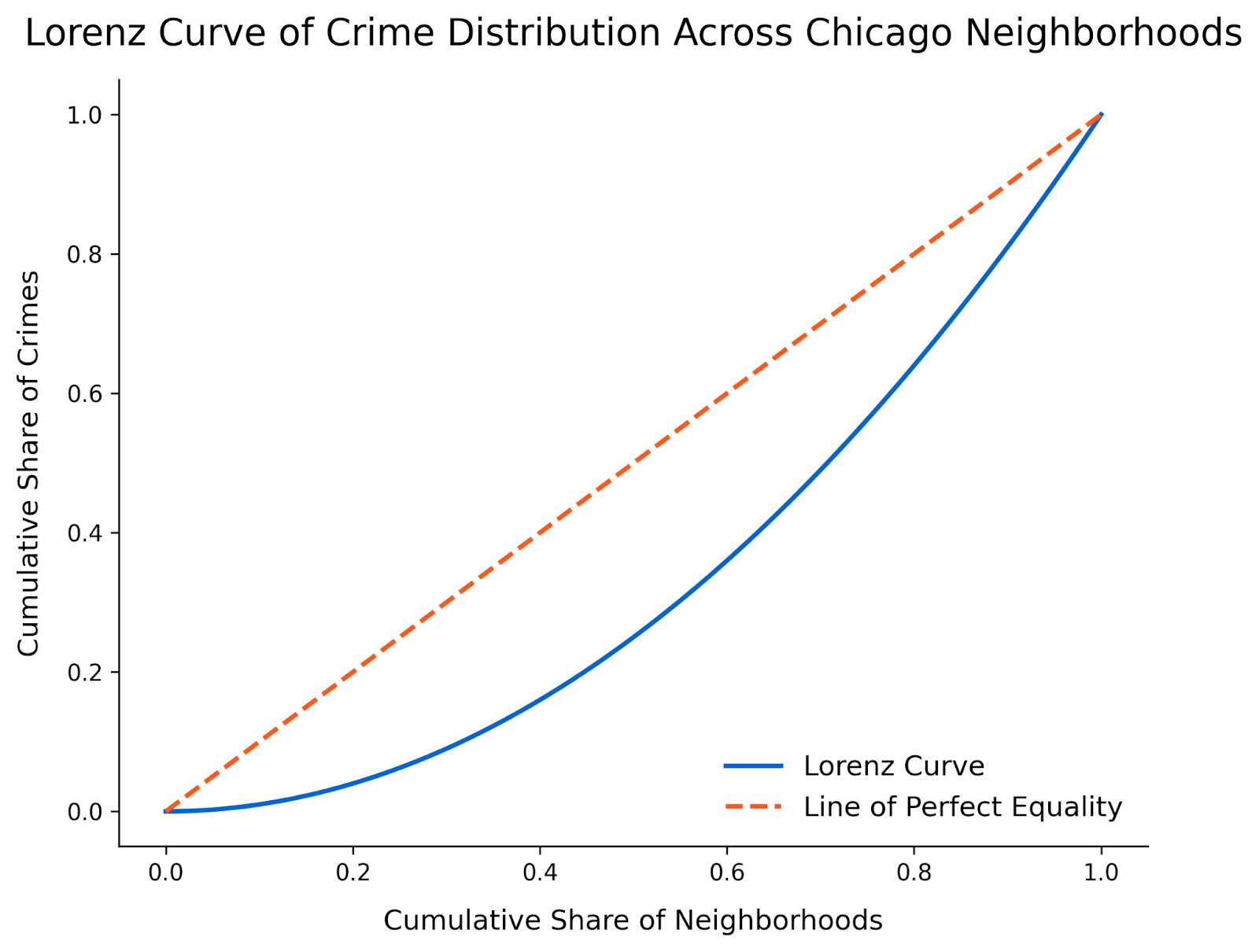
Etapa 5: Interpretar os resultados
Por fim, precisamos interpretar o gráfico. Essa curva de Lorenz revela uma desigualdade impressionante na distribuição de crimes entre os bairros de Chicago. A curva se afasta significativamente da linha de igualdade perfeita, mostrando que uma pequena fração de bairros é responsável pela maioria dos crimes denunciados.
Parece que os primeiros 50% dos bairros contribuem para menos de 20% do total de crimes, enquanto os demais bairros suportam a maior parte do ônus do crime. Essa visualização destaca padrões de desigualdade que podem não ser tão aparentes em outros tipos de gráficos. A próxima etapa pode ser a identificação de bairros com maior criminalidade para iniciar medidas de mitigação ou identificar bairros com menos criminalidade para ver quais impedimentos estão funcionando.
Esse exemplo demonstra como a curva de Lorenz pode ser aplicada além dos dados de renda para contar histórias interessantes sobre a desigualdade em outros campos. Ao analisar dados sobre crimes, podemos descobrir padrões de desigualdade que informam políticas públicas e decisões de planejamento urbano. Tente aplicar esse método a outros conjuntos de dados, como acesso à saúde, resultados educacionais ou dados ambientais, para explorar a desigualdade de maneiras novas e significativas.
Curva de Lorenz vs. Coeficiente de Gini
O coeficiente de Gini é derivado diretamente da curva de Lorenz. Ele mede a área entre a curva de Lorenz e a linha de igualdade perfeita. Uma área maior indica maior desigualdade, enquanto uma área menor sugere maior igualdade. O coeficiente de Gini varia de 0 a 1, sendo que 0 representa igualdade perfeita (todos têm recursos iguais) e 1 representa desigualdade extrema (um indivíduo detém todos os recursos).
A medida que você usará depende de seus objetivos. A curva de Lorenz mostra a forma da desigualdade, enquanto o coeficiente de Gini fornece um resumo numérico dela. Se você estiver analisando a quantidade de desigualdade em uma população, a curva de Lorenz oferecerá mais detalhes. No entanto, se você estiver comparando várias populações entre si, comparar as curvas de Lorenz de cada uma delas pode ser complicado, portanto, o coeficiente de Gini pode ser mais apropriado. Para se aprofundar no coeficiente de Gini, confira meu tutorial Entendendo o Coeficiente de Gini.
Além disso, devemos dizer que a curva de Lorenz talvez seja mais flexível, pois pode ser aplicada a vários tipos de dados, incluindo renda, criminalidade, acesso à saúde ou biodiversidade, e usada para comparar distribuições ao longo do tempo ou entre grupos. O coeficiente de Gini também pode ser usado para esses tipos de comparações, mas tem a reputação de ser usado principalmente para medir a desigualdade de renda. Isso pode criar um viés para alguns consumidores. Em minha experiência, as pessoas tendem a ter menos preconceitos ao interpretar gráficos do que quando recebem um número.
| Recurso | Curva de Lorenz | Coeficiente de Gini |
|---|---|---|
| Finalidade | Mostra a distribuição de recursos em uma população | Resume a desigualdade em um único valor |
| Tipo | Representação visual | Representação numérica |
| Interpretação | O formato da curva indica o grau de desigualdade | O valor varia de 0 (igualdade perfeita) a 1 (desigualdade extrema) |
| Casos de uso | Comparação de distribuições, identificação de padrões e comunicação de descobertas | Comparação dos níveis de desigualdade entre conjuntos de dados ou populações |
| Flexibilidade | Pode ser aplicado a vários conjuntos de dados (por exemplo, renda, crime, biodiversidade) | Usado principalmente para desigualdade de renda ou riqueza |
| Capacidade de ação | Ajuda a identificar áreas específicas de desigualdade para intervenções direcionadas | Fornece um resumo de alto nível para comparações amplas |
A comparação acima destaca como a curva de Lorenz e o coeficiente de Gini se complementam. A curva de Lorenz oferece uma perspectiva mais detalhada e visual para uma população, enquanto o coeficiente de Gini fornece um resumo conciso que pode ser usado para comparar populações.
Aplicações da curva de Lorenz no mundo real
A curva de Lorenz é uma ferramenta versátil que tem sido aplicada em uma ampla variedade de campos. Vamos explorar algumas de suas aplicações mais impactantes.
- A curva de Lorenz em economia e finanças: A Curva de Lorenz é mais conhecida por ser usada para analisar a desigualdade de renda e riqueza. Economistas e formuladores de políticas dependem dela para entender como os recursos são distribuídos em uma população e para elaborar intervenções como políticas tributárias ou programas sociais.
- A curva de Lorenz em saúde pública e epidemiologia: Na saúde pública, a curva de Lorenz pode ser usada para medir as desigualdades nos resultados de saúde ou no acesso à assistência médica. Isso ajuda pesquisadores e formuladores de políticas a identificar disparidades e alocar recursos de forma mais eficaz.
- A curva de Lorenz em ecologia e biodiversidade: Os ecologistas podem usar a curva de Lorenz para estudar a distribuição e a abundância das espécies. Ele pode ajudar a quantificar a biodiversidade e identificar ecossistemas onde algumas espécies dominam enquanto outras são escassas.
- A curva de Lorenz na ciência de dados e no machine learning: A curva de Lorenz está sendo cada vez mais usada na ciência de dados para analisar distribuições e avaliar a imparcialidade em modelos preditivos. Um exemplo disso é a análise de clientes. As empresas podem usar a curva de Lorenz para entender a concentração de receita entre os clientes. Ele pode ajudar a identificar quais usuários geram a maior parte da receita, possivelmente informando estratégias de marketing ou programas de fidelidade.
- A curva de Lorenz na ciência de dados e no machine learning: Outro exemplo que fiquei surpreso ao saber é o machine learning. A curva de Lorenz pode ajudar os cientistas de dados a avaliar se as previsões de um modelo são tendenciosas. Por exemplo, em um modelo de aprovação de empréstimos, a curva pode revelar que um pequeno grupo de solicitantes recebe a maioria das aprovações, o que indica um possível viés no algoritmo.
Vantagens e limitações da curva de Lorenz
Como qualquer método, a curva de Lorenz tem seus pontos fortes e fracos.
Limitações da curva de Lorenz
A curva de Lorenz geralmente requer dados bastante granulares para produzir resultados significativos. Conjuntos de dados agregados ou incompletos podem, às vezes, levar a conclusões imprecisas. Por exemplo, dados de renda que excluem ganhos informais, como gorjetas, podem subestimar a desigualdade.
Também é importante ter um tamanho de amostra grande o suficiente para garantir uma curva em vez de uma linha irregular, que você pode ver na primeira figura. Como sempre, é importante garantir que seus dados sejam os mais completos possíveis. E, é claro, você deve validar cuidadosamente seus dados e documentar todas as suposições feitas para garantir transparência e confiabilidade.
A curva de Lorenz também não capta a desigualdade multidimensional. Ele se concentra em uma única variável, como renda ou patrimônio, e não leva em conta nenhum efeito combinado. Entretanto, se você quiser medir a desigualdade multidimensional, há outras ferramentas que podem ser usadas, como o Índice de Pobreza Multidimensional.
Vantagens da curva de Lorenz
A maior vantagem da curva de Lorenz, em minha opinião, é que ela fornece uma representação visual intuitiva da desigualdade, facilitando a compreensão em um piscar de olhos. Ao comparar a curva com a linha de igualdade perfeita, as disparidades em uma população tornam-se imediatamente aparentes. É uma ferramenta de narrativa visual que torna os dados sobre desigualdade acessíveis a públicos técnicos e não técnicos.
Sua versatilidade é outra grande vantagem. A curva de Lorenz pode ser aplicada em vários campos, desde a economia e a saúde pública até a ecologia e o machine learning. Essa flexibilidade o torna amplamente útil.
Conclusão
A curva de Lorenz é uma ferramenta versátil para contar histórias que é útil para exibir e entender a desigualdade. Se esse tipo de visualização lhe interessa, você pode gostar de ler Geometric Mean: Uma medida para o crescimento e a composição. Ou, se você quiser saber mais sobre finanças, recomendo que confira nosso curso Introdução ao Python para finanças e nosso programa de habilidades Finanças aplicadas em Python.

Sou PhD e tenho 13 anos de experiência trabalhando com dados em um ambiente de pesquisa biológica. Crio software em várias linguagens de programação, incluindo Python, MATLAB e R. Sou apaixonado por compartilhar meu amor pelo aprendizado com o mundo.
Perguntas frequentes
O que é a curva de Lorenz?
A curva de Lorenz é um gráfico que mostra a quantidade de desigualdade de um recurso em uma população.
A curva de Lorenz é a mesma que o Índice de Gini?
O Índice de Gini, ou coeficiente de Gini, usa a curva de Lorenz em seu cálculo. Mas são métricas diferentes.
Como você interpreta uma curva de Lorenz?
De modo geral, quanto mais a curva se afasta da linha de igualdade, maior é a desigualdade na distribuição.
A curva de Lorenz é apenas para renda?
Embora tenha sido originalmente desenvolvida para a renda, a curva de Lorenz pode ser usada para dados tão díspares quanto serviços de saúde, crime, biodiversidade e machine learning.
Qual é a linha de igualdade?
A linha de igualdade é uma linha diagonal reta que representa a igualdade perfeita, ou seja, todos têm a mesma quantidade de um recurso.
Perguntas frequentes sobre a curva de Lorenz
O que é a curva de Lorenz?
A curva de Lorenz é um gráfico que mostra a quantidade de desigualdade de um recurso em uma população.
A curva de Lorenz é a mesma que o Índice de Gini?
O Índice de Gini, ou Coeficiente de Gini, usa a curva de Lorenz em seu cálculo. Mas são métricas diferentes.
Como você interpreta uma curva de Lorenz?
De modo geral, quanto mais a curva se afasta da linha de igualdade, maior é a desigualdade na distribuição.
A curva de Lorenz é apenas para renda?
Embora tenha sido originalmente desenvolvida para a renda, a curva de Lorenz pode ser usada para dados tão díspares quanto serviços de saúde, crime, biodiversidade e machine learning.
Qual é a linha de igualdade?
A linha de igualdade é uma linha diagonal reta que representa a igualdade perfeita, ou seja, todos têm a mesma quantidade de um recurso.


