Cours
Dans ce tutoriel, vous verrez comment vous pouvez utiliser un modèle de séries temporelles connu sous le nom de Mémoire à long terme. Les modèles LSTM sont puissants, en particulier pour conserver une mémoire à long terme, de par leur conception, comme vous le verrez plus loin. Vous aborderez les sujets suivants dans ce tutoriel :
- Comprenez pourquoi vous devez être capable de prédire l'évolution du cours des actions ;
- Téléchargez les données - Vous utiliserez des données boursières recueillies sur Yahoo finance ;
- Divisez les données de formation et de test et effectuez également une normalisation des données ;
- Passez en revue et appliquez quelques techniques de calcul de moyenne qui peuvent être utilisées pour les prédictions à un pas d'avance ;
- Motivez et présentez brièvement un modèle LSTM qui permet de prédire plus d'une étape à l'avance ;
- Prédire et visualiser l'avenir des marchés boursiers à partir de données actuelles
Si vous n'êtes pas familier avec le deep learning ou les réseaux neuronaux, vous devriez jeter un coup d'œil à notre cours Deep Learning in Python. Il couvre les bases, ainsi que la façon de construire un réseau neuronal par vous-même dans Keras. Il s'agit d'un package différent de TensorFlow, qui sera utilisé dans ce tutoriel, mais l'idée est la même.
Pourquoi avez-vous besoin de modèles de séries temporelles ?
Vous aimeriez modéliser correctement les cours des actions afin de pouvoir, en tant qu'acheteur d'actions, décider raisonnablement quand acheter des actions et quand les vendre pour réaliser un bénéfice. C'est là qu'intervient la modélisation des séries chronologiques. Vous avez besoin de bons modèles d'apprentissage automatique capables d'examiner l'historique d'une séquence de données et de prédire correctement les futurs éléments de cette séquence.
Avertissement: Les prix des marchés boursiers sont très imprévisibles et volatils. Cela signifie qu'il n'y a pas de modèles cohérents dans les données qui vous permettent de modéliser presque parfaitement les prix des actions dans le temps. Ne vous fiez pas à moi, mais plutôt à Burton Malkiel, économiste à l'université de Princeton, qui affirme dans son livre de 1973, "A Random Walk Down Wall Street", que si le marché est vraiment efficace et que le prix d'une action reflète tous les facteurs dès qu'ils sont rendus publics, un singe aux yeux bandés lançant des fléchettes sur une liste d'actions publiée dans un journal devrait faire aussi bien que n'importe quel professionnel de l'investissement.
Cependant, il ne faut pas croire qu'il s'agit d'un processus stochastique ou aléatoire et qu'il n'y a pas d'espoir pour l'apprentissage automatique. Voyons si vous pouvez au moins modéliser les données, de sorte que les prédictions que vous faites soient en corrélation avec le comportement réel des données. En d'autres termes, vous n'avez pas besoin des valeurs exactes des actions dans le futur, mais de l'évolution du cours des actions (c'est-à-dire de savoir s'il va augmenter ou diminuer dans un avenir proche).
# Make sure that you have all these libaries available to run the code successfully
from pandas_datareader import data
import matplotlib.pyplot as plt
import pandas as pd
import datetime as dt
import urllib.request, json
import os
import numpy as np
import tensorflow as tf # This code has been tested with TensorFlow 1.6
from sklearn.preprocessing import MinMaxScalerTéléchargement des données
Vous utiliserez des données provenant des sources suivantes :
-
Alpha Vantage Stock API. Avant de commencer, vous aurez besoin d'une clé API, que vous pouvez obtenir gratuitement ici. Ensuite, vous pouvez assigner cette touche à la variable
api_key. Dans ce tutoriel, nous allons récupérer 20 ans de données historiques pour l'action American Airlines. En option, vous pouvez consulter ce guide de démarrage de l'API boursière pour connaître les meilleures pratiques en matière d'utilisation des données historiques du marché. -
Utilisez les données de cette page. Vous devrez copier le dossier Stocks du fichier zip dans le dossier d'accueil de votre projet.
Les cours des actions se présentent sous différentes formes. Il s'agit de
- Ouvrir : Cours d'ouverture de la bourse du jour
- Fermer : Cours de clôture du jour
- Haut : Cours le plus élevé des données
- Faible : Cours le plus bas de la journée
Obtenir des données d'Alphavantage
Vous commencerez par charger les données d'Alpha Vantage. Comme vous allez utiliser les cours de l'action American Airlines pour faire vos prévisions, vous fixez le ticker à "AAL". En outre, vous définissez également un fichier url_string, qui renverra un fichier JSON contenant toutes les données boursières relatives à American Airlines au cours des 20 dernières années, et un fichier file_to_save, qui sera le fichier dans lequel vous sauvegarderez les données. Vous utiliserez la variable ticker que vous avez définie au préalable pour vous aider à nommer ce fichier.
Ensuite, vous allez spécifier une condition : si vous n'avez pas encore sauvegardé les données, vous allez aller de l'avant et récupérer les données à partir de l'URL que vous avez défini dans url_string; Vous allez stocker les valeurs de date, bas, haut, volume, fermeture, ouverture dans un DataFrame pandas df et vous allez le sauvegarder à file_to_save. Toutefois, si les données sont déjà présentes, vous les chargerez simplement à partir du fichier CSV.
Obtenir des données de Kaggle
Les données trouvées sur Kaggle sont une collection de fichiers csv et vous n'avez pas besoin de faire de prétraitement, vous pouvez donc directement charger les données dans un DataFrame Pandas.
data_source = 'kaggle' # alphavantage or kaggle
if data_source == 'alphavantage':
# ====================== Loading Data from Alpha Vantage ==================================
api_key = '<your API key>'
# American Airlines stock market prices
ticker = "AAL"
# JSON file with all the stock market data for AAL from the last 20 years
url_string = "https://www.alphavantage.co/query?function=TIME_SERIES_DAILY&symbol=%s&outputsize=full&apikey=%s"%(ticker,api_key)
# Save data to this file
file_to_save = 'stock_market_data-%s.csv'%ticker
# If you haven't already saved data,
# Go ahead and grab the data from the url
# And store date, low, high, volume, close, open values to a Pandas DataFrame
if not os.path.exists(file_to_save):
with urllib.request.urlopen(url_string) as url:
data = json.loads(url.read().decode())
# extract stock market data
data = data['Time Series (Daily)']
df = pd.DataFrame(columns=['Date','Low','High','Close','Open'])
for k,v in data.items():
date = dt.datetime.strptime(k, '%Y-%m-%d')
data_row = [date.date(),float(v['3. low']),float(v['2. high']),
float(v['4. close']),float(v['1. open'])]
df.loc[-1,:] = data_row
df.index = df.index + 1
print('Data saved to : %s'%file_to_save)
df.to_csv(file_to_save)
# If the data is already there, just load it from the CSV
else:
print('File already exists. Loading data from CSV')
df = pd.read_csv(file_to_save)
else:
# ====================== Loading Data from Kaggle ==================================
# You will be using HP's data. Feel free to experiment with other data.
# But while doing so, be careful to have a large enough dataset and also pay attention to the data normalization
df = pd.read_csv(os.path.join('Stocks','hpq.us.txt'),delimiter=',',usecols=['Date','Open','High','Low','Close'])
print('Loaded data from the Kaggle repository')
Data saved to : stock_market_data-AAL.csv
Data Exploration
Vous imprimez ici les données que vous avez collectées dans le DataFrame. Vous devez également vous assurer que les données sont triées par date, car l'ordre des données est crucial dans la modélisation des séries temporelles.
# Sort DataFrame by date
df = df.sort_values('Date')
# Double check the result
df.head()
| Date | Ouvrir | Haut | Faible | Fermer | |
|---|---|---|---|---|---|
| 0 | 1970-01-02 | 0.30627 | 0.30627 | 0.30627 | 0.30627 |
| 1 | 1970-01-05 | 0.30627 | 0.31768 | 0.30627 | 0.31385 |
| 2 | 1970-01-06 | 0.31385 | 0.31385 | 0.30996 | 0.30996 |
| 3 | 1970-01-07 | 0.31385 | 0.31385 | 0.31385 | 0.31385 |
| 4 | 1970-01-08 | 0.31385 | 0.31768 | 0.31385 | 0.31385 |
Visualisation des données
Voyons maintenant quel type de données vous avez. Vous souhaitez obtenir des données présentant différents schémas au fil du temps.
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),(df['Low']+df['High'])/2.0)
plt.xticks(range(0,df.shape[0],500),df['Date'].loc[::500],rotation=45)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.show()
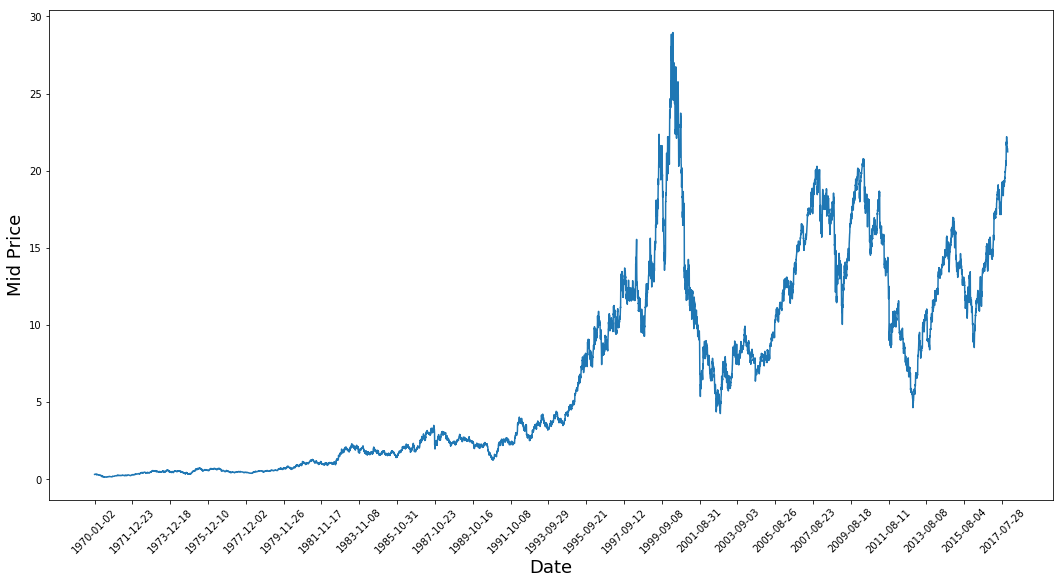
Ce graphique dit déjà beaucoup de choses. La raison pour laquelle j'ai choisi cette entreprise plutôt qu'une autre est que ce graphique est rempli de comportements différents des prix des actions au fil du temps. Cela rendra l'apprentissage plus robuste et vous permettra de tester la qualité des prédictions dans diverses situations.
Il convient également de noter que les valeurs proches de 2017 sont beaucoup plus élevées et fluctuent davantage que les valeurs proches des années 1970. Vous devez donc vous assurer que les données se comportent dans des fourchettes de valeurs similaires tout au long de la période. Vous vous en occuperez lors de la phase de normalisation des données.
Diviser les données en un ensemble de formation et un ensemble de test
Vous utiliserez le prix moyen calculé en prenant la moyenne des prix les plus élevés et les plus bas enregistrés au cours d'une journée.
# First calculate the mid prices from the highest and lowest
high_prices = df.loc[:,'High'].as_matrix()
low_prices = df.loc[:,'Low'].as_matrix()
mid_prices = (high_prices+low_prices)/2.0
Vous pouvez maintenant diviser les données de formation et les données de test. Les données d'apprentissage seront les 11 000 premiers points de données de la série temporelle et le reste sera constitué de données de test.
train_data = mid_prices[:11000]
test_data = mid_prices[11000:]
Normaliser les données
Vous devez maintenant définir une échelle pour normaliser les données. MinMaxScalar met à l'échelle toutes les données pour qu'elles soient comprises entre 0 et 1. Vous pouvez également remodeler les données d'apprentissage et de test pour qu'elles aient la forme [data_size, num_features].
# Scale the data to be between 0 and 1
# When scaling remember! You normalize both test and train data with respect to training data
# Because you are not supposed to have access to test data
scaler = MinMaxScaler()
train_data = train_data.reshape(-1,1)
test_data = test_data.reshape(-1,1)
En raison de l'observation que vous avez faite précédemment, à savoir que les différentes périodes de données ont des plages de valeurs différentes, vous normalisez les données en divisant la série complète en fenêtres. Si vous ne le faites pas, les données antérieures seront proches de 0 et n'ajouteront pas beaucoup de valeur au processus d'apprentissage. Vous choisissez ici une taille de fenêtre de 2500.
Conseil: lorsque vous choisissez la taille de la fenêtre, assurez-vous qu'elle n'est pas trop petite, car lorsque vous effectuez une normalisation par fenêtre, cela peut introduire une rupture à la toute fin de chaque fenêtre, étant donné que chaque fenêtre est normalisée indépendamment.
Dans cet exemple, 4 points de données seront concernés. Mais étant donné que vous avez 11 000 points de données, 4 points ne poseront pas de problème.
# Train the Scaler with training data and smooth data
smoothing_window_size = 2500
for di in range(0,10000,smoothing_window_size):
scaler.fit(train_data[di:di+smoothing_window_size,:])
train_data[di:di+smoothing_window_size,:] = scaler.transform(train_data[di:di+smoothing_window_size,:])
# You normalize the last bit of remaining data
scaler.fit(train_data[di+smoothing_window_size:,:])
train_data[di+smoothing_window_size:,:] = scaler.transform(train_data[di+smoothing_window_size:,:])
Remodeler les données pour qu'elles reprennent la forme de [data_size]
# Reshape both train and test data
train_data = train_data.reshape(-1)
# Normalize test data
test_data = scaler.transform(test_data).reshape(-1)
Vous pouvez maintenant lisser les données à l'aide de la moyenne mobile exponentielle. Cela vous permet de vous débarrasser des irrégularités inhérentes aux données des cours boursiers et de produire une courbe plus lisse.
Notez que vous ne devez lisser que les données de formation.
# Now perform exponential moving average smoothing
# So the data will have a smoother curve than the original ragged data
EMA = 0.0
gamma = 0.1
for ti in range(11000):
EMA = gamma*train_data[ti] + (1-gamma)*EMA
train_data[ti] = EMA
# Used for visualization and test purposes
all_mid_data = np.concatenate([train_data,test_data],axis=0)
Prédiction en une étape par calcul de moyenne
Les mécanismes de calcul de moyenne vous permettent de faire des prévisions (souvent un pas de temps à l'avance) en représentant le prix futur des actions comme une moyenne des prix des actions observés précédemment. Faire cela pour plus d'un pas de temps peut produire des résultats assez mauvais. Vous trouverez ci-dessous deux techniques de calcul de la moyenne : la moyenne standard et la moyenne mobile exponentielle. Vous évaluerez qualitativement (inspection visuelle) et quantitativement (erreur quadratique moyenne) les résultats produits par les deux algorithmes.
L'erreur quadratique moyenne (EQM) peut être calculée en prenant l'erreur quadratique entre la valeur réelle à un pas en avant et la valeur prédite et en faisant la moyenne de toutes les prédictions.
Moyenne standard
Vous pouvez comprendre la difficulté de ce problème en essayant d'abord de le modéliser comme un problème de calcul moyen. Tout d'abord, vous essayez de prédire les futurs prix du marché boursier (par exemple, xt+1 ) en tant que moyenne des prix du marché boursier observés précédemment dans une fenêtre de taille fixe (par exemple, xt-N, ..., xt) (disons les 100 jours précédents). Par la suite, vous essayerez une méthode un peu plus fantaisiste de "moyenne mobile exponentielle" et vous verrez si elle donne de bons résultats. Vous passerez ensuite au "Saint-Graal" de la prédiction des séries temporelles : les modèles de mémoire à long terme.
Vous verrez tout d'abord comment fonctionne le calcul de la moyenne normale. C'est-à-dire que vous dites,
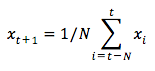
En d'autres termes, vous dites que la prédiction à $t+1$ est la valeur moyenne de tous les prix des actions que vous avez observés dans une fenêtre allant de $t$ à $t-N$.
window_size = 100
N = train_data.size
std_avg_predictions = []
std_avg_x = []
mse_errors = []
for pred_idx in range(window_size,N):
if pred_idx >= N:
date = dt.datetime.strptime(k, '%Y-%m-%d').date() + dt.timedelta(days=1)
else:
date = df.loc[pred_idx,'Date']
std_avg_predictions.append(np.mean(train_data[pred_idx-window_size:pred_idx]))
mse_errors.append((std_avg_predictions[-1]-train_data[pred_idx])**2)
std_avg_x.append(date)
print('MSE error for standard averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for standard averaging: 0.00418
Vous trouverez ci-dessous la moyenne des résultats. Il suit de très près le comportement réel des actions. Ensuite, vous examinerez une méthode de prédiction en une étape plus précise.
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')
plt.plot(range(window_size,N),std_avg_predictions,color='orange',label='Prediction')
#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)
plt.xlabel('Date')
plt.ylabel('Mid Price')
plt.legend(fontsize=18)
plt.show()
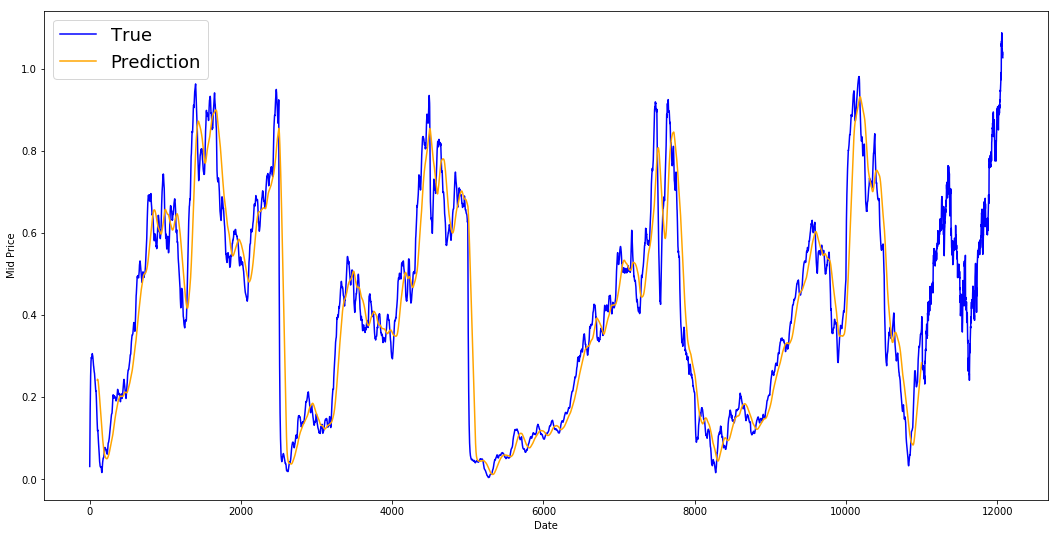
Que disent donc les graphiques ci-dessus (et l'EQM) ?
Il semble que ce modèle ne soit pas trop mauvais pour les prévisions à très court terme (un jour à l'avance). Étant donné que les prix des actions ne passent pas de 0 à 100 du jour au lendemain, ce comportement est raisonnable. Ensuite, vous examinerez une technique de calcul de moyenne plus sophistiquée, la moyenne mobile exponentielle.
Moyenne mobile exponentielle
Vous avez peut-être vu sur Internet des articles utilisant des modèles très complexes et prédisant presque exactement le comportement du marché boursier. Mais attention ! Il s'agit d'illusions d'optique et non d'un apprentissage utile. Vous verrez ci-dessous comment reproduire ce comportement à l'aide d'une simple méthode de calcul de la moyenne.
Dans la méthode de la moyenne mobile exponentielle, vous calculez $x_{t+1}$ comme suit,
- x\_{t+1} = EMA\_{t} = \gamma \times EMA_{t-1} + (1-\gamma) x_t$ où $EMA_0 = 0$ et $EMA$ est la valeur de la moyenne mobile exponentielle que vous maintenez dans le temps.
L'équation ci-dessus calcule la moyenne mobile exponentielle à partir du pas de temps $t+1$ et l'utilise comme prédiction à un pas en avant. Le paramètre $\gamma$ détermine la contribution de la prédiction la plus récente à l'EMA. Par exemple, un $\gamma=0,1$ ne permet d'intégrer que 10% de la valeur actuelle dans l'EMA. Comme vous ne prenez qu'une très petite partie des valeurs les plus récentes, cela permet de préserver des valeurs beaucoup plus anciennes que vous avez vues très tôt dans la moyenne. Voyez l'efficacité de cette méthode lorsqu'elle est utilisée pour prédire une avance d'un pas ci-dessous.
window_size = 100
N = train_data.size
run_avg_predictions = []
run_avg_x = []
mse_errors = []
running_mean = 0.0
run_avg_predictions.append(running_mean)
decay = 0.5
for pred_idx in range(1,N):
running_mean = running_mean*decay + (1.0-decay)*train_data[pred_idx-1]
run_avg_predictions.append(running_mean)
mse_errors.append((run_avg_predictions[-1]-train_data[pred_idx])**2)
run_avg_x.append(date)
print('MSE error for EMA averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for EMA averaging: 0.00003
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')
plt.plot(range(0,N),run_avg_predictions,color='orange', label='Prediction')
#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)
plt.xlabel('Date')
plt.ylabel('Mid Price')
plt.legend(fontsize=18)
plt.show()
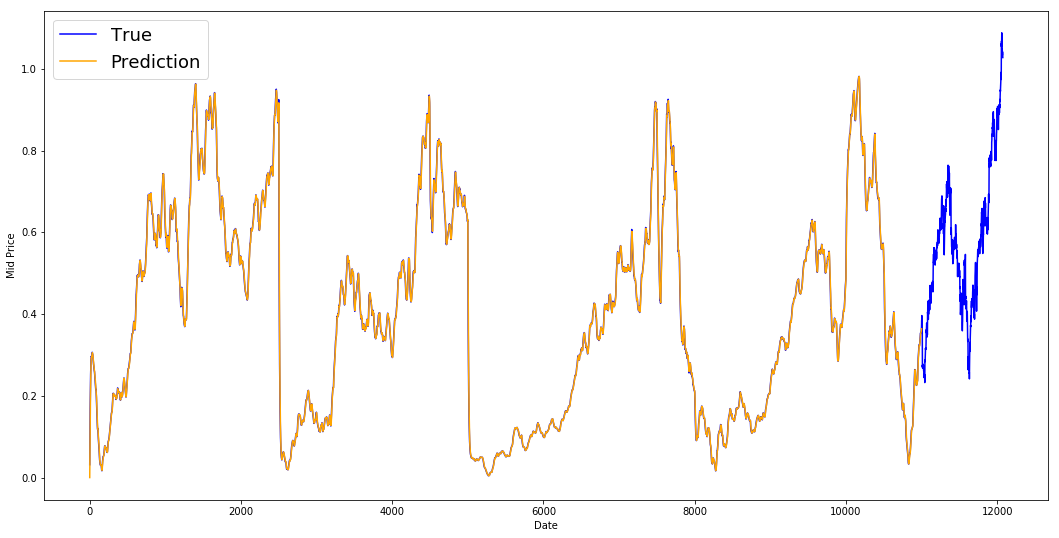
Si la moyenne mobile exponentielle est aussi bonne, pourquoi avez-vous besoin de meilleurs modèles ?
Vous voyez qu'il s'agit d'une ligne parfaite qui suit la distribution True (ce qui est justifié par le très faible MSE). En pratique, vous ne pouvez pas faire grand-chose avec la seule valeur boursière du lendemain. Personnellement, je n'aimerais pas connaître le cours exact de la bourse pour le lendemain, mais savoir si les cours de la bourse augmenteront ou diminueront au cours des 30 prochains jours. Essayez de le faire et vous mettrez en évidence l'incapacité de la méthode EMA.
Vous allez maintenant essayer de faire des prédictions par fenêtre (par exemple, vous allez prédire la fenêtre des deux prochains jours, au lieu du jour suivant). Vous réaliserez alors à quel point l'EMA peut mal tourner. En voici un exemple :
Prévoir plus d'un pas dans l'avenir
Pour rendre les choses plus concrètes, supposons des valeurs, disons $x_t=0,4$, $EMA=0,5$ et $\gamma = 0,5$.
- Supposons que vous obteniez la sortie avec l'équation suivante
- Xt+1 = EMAt = γ × EMAt-1 + (1 - γ)Xt
- Vous avez donc xt+1 = 0,5 × 0,5 + (1-0,5) × 0,4 = 0,45
- Donc Xt+1 = EMAt = 0,45
- La prédiction suivante Xt+2 devient donc,
- Xt+2 = γ × EMAt + (1-γ)Xt+1
- Soit Xt+2 = γ × EMA_t + (1-γ) EMAt = EMAt
- Ou, dans cet exemple, Xt+2 = Xt+1 = 0,45
Ainsi, quel que soit le nombre d'étapes de prédiction dans le futur, vous obtiendrez toujours la même réponse pour toutes les étapes de prédiction dans le futur.
Une solution qui vous permettra d'obtenir des informations utiles consiste à utiliser des algorithmes basés sur le momentum. Ils font des prédictions en se basant sur la hausse ou la baisse des valeurs récentes (et non sur les valeurs exactes). Par exemple, ils diront que le prix du lendemain sera probablement plus bas si les prix ont baissé au cours des derniers jours, ce qui semble raisonnable. Cependant, vous utiliserez un modèle plus complexe : un modèle LSTM.
Ces modèles ont pris d'assaut le domaine de la prévision des séries temporelles, parce qu'ils modélisent très bien les données des séries temporelles. Vous verrez s'il existe des modèles cachés dans les données que vous pouvez exploiter.
Introduction aux LSTM : Faire des prévisions sur les mouvements boursiers dans un avenir lointain
Les modèles de mémoire à long terme sont des modèles de séries temporelles extrêmement puissants. Ils peuvent prédire un nombre arbitraire d'étapes dans l'avenir. Un module (ou cellule) LSTM comporte 5 composants essentiels qui lui permettent de modéliser des données à long terme et à court terme.
- État de la cellule (ct) - Il s'agit de la mémoire interne de la cellule qui stocke à la fois la mémoire à court terme et la mémoire à long terme.
- État caché (ht) - Il s'agit de l'information sur l'état de sortie calculée en fonction de l'entrée actuelle, de l'état caché précédent et de l'entrée de la cellule actuelle, que vous utilisez finalement pour prédire les futurs prix du marché boursier. En outre, l'état caché peut décider de ne récupérer que la mémoire à court ou à long terme ou les deux types de mémoire stockés dans l'état cellulaire pour faire la prédiction suivante.
- Porte d'entrée (it) - Décide de la quantité d'informations provenant de l'entrée actuelle qui passe à l'état de la cellule.
- Porte d'oubli (ft) - Décide de la quantité d'informations provenant de l'entrée actuelle et de l'état précédent de la cellule qui passe dans l'état actuel de la cellule.
- Porte de sortie (ot) - Décide de la quantité d'informations provenant de l'état actuel de la cellule qui passe dans l'état caché, de sorte que, si nécessaire, la LSTM ne peut sélectionner que les souvenirs à long terme ou les souvenirs à court terme et les souvenirs à long terme.
Une cellule est illustrée ci-dessous.
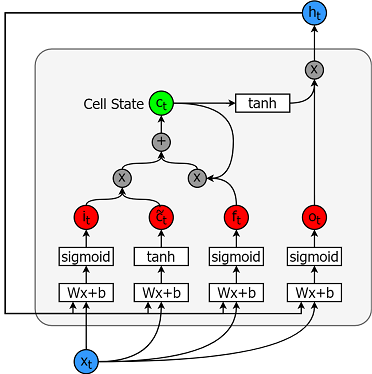
Les équations permettant de calculer chacune de ces entités sont les suivantes.
- it = σ(WixXt + Wihht-1 +bi)
- $tilde{c}\_t = \sigma(W\_{cx}x\_t + W\_{ch}h_{t-1} + b_c)$
- $f\_t = \sigma(W\_{fx}x\_t + W\_{fh}h_{t-1}+b_f)$
- $c_t = f\_t c\_{t-1} + i_t \tilde{c}_t$
- $o\_t = \sigma(W\_{ox}x\_t + W\_{oh}h_{t-1}+b_o)$
- h_t = o_t tanh(c_t) $h_t = o_t tanh(c_t) $h_t = o_t tanh(c_t)
Pour une meilleure compréhension (plus technique) des LSTM, vous pouvez consulter cet article.
TensorFlow fournit une sous-API intéressante (appelée RNN API) pour la mise en œuvre de modèles de séries temporelles. Vous l'utiliserez pour vos mises en œuvre.
Générateur de données
Vous allez d'abord mettre en place un générateur de données pour entraîner votre modèle. Ce générateur de données aura une méthode appelée .unroll_batches(...) qui produira un ensemble de lots num_unrollings de données d'entrée obtenues séquentiellement, où un lot de données est de taille [batch_size, 1]. À chaque lot de données d'entrée correspondra un lot de données de sortie.
Par exemple, si num_unrollings=3 et batch_size=4 un ensemble de lots déroulés, cela pourrait ressembler à ce qui suit,
- données d'entrée : $[x_0,x_10,x_20,x_30], [x_1,x_11,x_21,x_31], [x_2,x_12,x_22,x_32]$
- données de sortie : $[x_1,x_11,x_21,x_31], [x_2,x_12,x_22,x_32], [x_3,x_13,x_23,x_33]$
Augmentation des données
De plus, pour que votre modèle soit robuste, vous ne ferez pas en sorte que la sortie pour $x\_t$ soit toujours $x\_{t+1}$. Vous allez plutôt échantillonner au hasard une sortie de l'ensemble $x\_{t+1},x\_{t+2},\ldots,x_{t+N}$ où $N$ est une petite taille de fenêtre.
Vous faites ici l'hypothèse suivante :
- $x\_{t+1},x\_{t+2},\ldots,x_{t+N}$ ne seront pas très éloignés les uns des autres
Je pense personnellement qu'il s'agit d'une hypothèse raisonnable pour prédire les mouvements boursiers.
Vous trouverez ci-dessous une illustration visuelle de la création d'un lot de données.
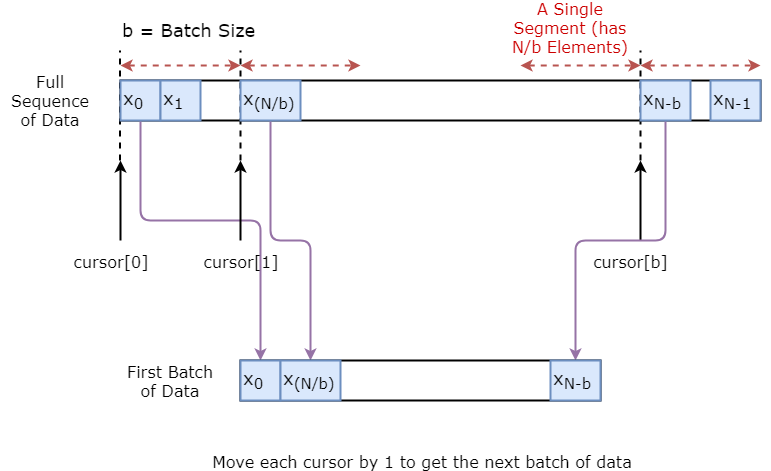
class DataGeneratorSeq(object):
def __init__(self,prices,batch_size,num_unroll):
self._prices = prices
self._prices_length = len(self._prices) - num_unroll
self._batch_size = batch_size
self._num_unroll = num_unroll
self._segments = self._prices_length //self._batch_size
self._cursor = [offset * self._segments for offset in range(self._batch_size)]
def next_batch(self):
batch_data = np.zeros((self._batch_size),dtype=np.float32)
batch_labels = np.zeros((self._batch_size),dtype=np.float32)
for b in range(self._batch_size):
if self._cursor[b]+1>=self._prices_length:
#self._cursor[b] = b * self._segments
self._cursor[b] = np.random.randint(0,(b+1)*self._segments)
batch_data[b] = self._prices[self._cursor[b]]
batch_labels[b]= self._prices[self._cursor[b]+np.random.randint(0,5)]
self._cursor[b] = (self._cursor[b]+1)%self._prices_length
return batch_data,batch_labels
def unroll_batches(self):
unroll_data,unroll_labels = [],[]
init_data, init_label = None,None
for ui in range(self._num_unroll):
data, labels = self.next_batch()
unroll_data.append(data)
unroll_labels.append(labels)
return unroll_data, unroll_labels
def reset_indices(self):
for b in range(self._batch_size):
self._cursor[b] = np.random.randint(0,min((b+1)*self._segments,self._prices_length-1))
dg = DataGeneratorSeq(train_data,5,5)
u_data, u_labels = dg.unroll_batches()
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
print('\n\nUnrolled index %d'%ui)
dat_ind = dat
lbl_ind = lbl
print('\tInputs: ',dat )
print('\n\tOutput:',lbl)
Unrolled index 0
Inputs: [0.03143791 0.6904868 0.82829314 0.32585657 0.11600105]
Output: [0.08698314 0.68685144 0.8329321 0.33355275 0.11785509]
Unrolled index 1
Inputs: [0.06067836 0.6890754 0.8325337 0.32857886 0.11785509]
Output: [0.15261841 0.68685144 0.8325337 0.33421066 0.12106793]
Unrolled index 2
Inputs: [0.08698314 0.68685144 0.8329321 0.33078218 0.11946969]
Output: [0.11098009 0.6848606 0.83387965 0.33421066 0.12106793]
Unrolled index 3
Inputs: [0.11098009 0.6858036 0.83294916 0.33219692 0.12106793]
Output: [0.132895 0.6836884 0.83294916 0.33219692 0.12288672]
Unrolled index 4
Inputs: [0.132895 0.6848606 0.833369 0.33355275 0.12158521]
Output: [0.15261841 0.6836884 0.83383167 0.33355275 0.12230608]
Définition des hyperparamètres
Dans cette section, vous définirez plusieurs hyperparamètres. D est la dimensionnalité de l'entrée. C'est simple, vous prenez le cours précédent de l'action en entrée et vous prédisez le cours suivant, qui devrait être 1.
Vous avez ensuite num_unrollings, qui est un hyperparamètre lié à la rétropropagation dans le temps (BPTT) utilisée pour optimiser le modèle LSTM. Cela indique le nombre de pas de temps continus que vous considérez pour une seule étape d'optimisation. Au lieu d'optimiser le modèle en examinant un seul pas de temps, vous optimisez le réseau en examinant num_unrollings pas de temps. Plus il est grand, mieux c'est.
Ensuite, vous avez le site batch_size. La taille du lot est le nombre d'échantillons de données que vous considérez dans un seul pas de temps.
Ensuite, vous définissez num_nodes qui représente le nombre de neurones cachés dans chaque cellule. Vous pouvez voir qu'il y a trois couches de LSTM dans cet exemple.
D = 1 # Dimensionality of the data. Since your data is 1-D this would be 1
num_unrollings = 50 # Number of time steps you look into the future.
batch_size = 500 # Number of samples in a batch
num_nodes = [200,200,150] # Number of hidden nodes in each layer of the deep LSTM stack we're using
n_layers = len(num_nodes) # number of layers
dropout = 0.2 # dropout amount
tf.reset_default_graph() # This is important in case you run this multiple times
Définir les entrées et les sorties
Ensuite, vous définissez des espaces réservés pour les entrées et les étiquettes de formation. Cette opération est très simple, car vous disposez d'une liste de champs d'entrée, chaque champ contenant un seul lot de données. Et la liste contient num_unrollings placeholders, qui seront utilisés en une seule fois pour une étape d'optimisation.
# Input data.
train_inputs, train_outputs = [],[]
# You unroll the input over time defining placeholders for each time step
for ui in range(num_unrollings):
train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,D],name='train_inputs_%d'%ui))
train_outputs.append(tf.placeholder(tf.float32, shape=[batch_size,1], name = 'train_outputs_%d'%ui))
Définition des paramètres des couches LSTM et Régression
Vous disposerez de trois couches de LSTM et d'une couche de régression linéaire, désignées par w et b, qui prendront la sortie de la dernière cellule de mémoire à long terme et produiront la prédiction pour le pas de temps suivant. Vous pouvez utiliser MultiRNNCell dans TensorFlow pour encapsuler les trois objets LSTMCell que vous avez créés. En outre, vous pouvez utiliser les cellules LSTM implémentées en dropout, car elles améliorent les performances et réduisent l'overfitting.
lstm_cells = [
tf.contrib.rnn.LSTMCell(num_units=num_nodes[li],
state_is_tuple=True,
initializer= tf.contrib.layers.xavier_initializer()
)
for li in range(n_layers)]
drop_lstm_cells = [tf.contrib.rnn.DropoutWrapper(
lstm, input_keep_prob=1.0,output_keep_prob=1.0-dropout, state_keep_prob=1.0-dropout
) for lstm in lstm_cells]
drop_multi_cell = tf.contrib.rnn.MultiRNNCell(drop_lstm_cells)
multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)
w = tf.get_variable('w',shape=[num_nodes[-1], 1], initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable('b',initializer=tf.random_uniform([1],-0.1,0.1))
Calcul de la sortie du LSTM et alimentation de la couche de régression pour obtenir la prédiction finale.
Dans cette section, vous commencez par créer des variables TensorFlow (c et h) qui contiendront l'état de la cellule et l'état caché de la cellule de la mémoire à long terme. Ensuite, vous transformez la liste de train_inputs pour obtenir une forme de [num_unrollings, batch_size, D], ce qui est nécessaire pour calculer les résultats avec la fonction tf.nn.dynamic_rnn. Vous calculez ensuite les sorties LSTM à l'aide de la fonction tf.nn.dynamic_rnn et vous divisez la sortie en une liste de tenseurs num_unrolling. la perte entre les prédictions et les prix réels des actions.
# Create cell state and hidden state variables to maintain the state of the LSTM
c, h = [],[]
initial_state = []
for li in range(n_layers):
c.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
h.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
initial_state.append(tf.contrib.rnn.LSTMStateTuple(c[li], h[li]))
# Do several tensor transofmations, because the function dynamic_rnn requires the output to be of
# a specific format. Read more at: https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn
all_inputs = tf.concat([tf.expand_dims(t,0) for t in train_inputs],axis=0)
# all_outputs is [seq_length, batch_size, num_nodes]
all_lstm_outputs, state = tf.nn.dynamic_rnn(
drop_multi_cell, all_inputs, initial_state=tuple(initial_state),
time_major = True, dtype=tf.float32)
all_lstm_outputs = tf.reshape(all_lstm_outputs, [batch_size*num_unrollings,num_nodes[-1]])
all_outputs = tf.nn.xw_plus_b(all_lstm_outputs,w,b)
split_outputs = tf.split(all_outputs,num_unrollings,axis=0)
Calcul des pertes et optimiseur
Vous allez maintenant calculer la perte. Toutefois, vous devez noter qu'il existe une caractéristique unique lors du calcul de la perte. Pour chaque lot de prédictions et de sorties réelles, vous calculez l'erreur quadratique moyenne. Et vous faites la somme (et non la moyenne) de toutes ces pertes moyennes au carré. Enfin, vous définissez l'optimiseur que vous allez utiliser pour optimiser le réseau neuronal. Dans ce cas, vous pouvez utiliser Adam, qui est un optimiseur très récent et performant.
# When calculating the loss you need to be careful about the exact form, because you calculate
# loss of all the unrolled steps at the same time
# Therefore, take the mean error or each batch and get the sum of that over all the unrolled steps
print('Defining training Loss')
loss = 0.0
with tf.control_dependencies([tf.assign(c[li], state[li][0]) for li in range(n_layers)]+
[tf.assign(h[li], state[li][1]) for li in range(n_layers)]):
for ui in range(num_unrollings):
loss += tf.reduce_mean(0.5*(split_outputs[ui]-train_outputs[ui])**2)
print('Learning rate decay operations')
global_step = tf.Variable(0, trainable=False)
inc_gstep = tf.assign(global_step,global_step + 1)
tf_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
tf_min_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
learning_rate = tf.maximum(
tf.train.exponential_decay(tf_learning_rate, global_step, decay_steps=1, decay_rate=0.5, staircase=True),
tf_min_learning_rate)
# Optimizer.
print('TF Optimization operations')
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 5.0)
optimizer = optimizer.apply_gradients(
zip(gradients, v))
print('\tAll done')
Defining training Loss
Learning rate decay operations
TF Optimization operations
All done
Calculs liés à la prédiction
Vous définissez ici les opérations TensorFlow liées à la prédiction. Tout d'abord, définissez un espace réservé pour l'alimentation de l'entrée (sample_inputs), puis, comme pour l'étape de formation, définissez des variables d'état pour la prédiction (sample_c et sample_h). Enfin, vous calculez la prédiction à l'aide de la fonction tf.nn.dynamic_rnn, puis vous envoyez la sortie à travers la couche de régression (w et b). Vous devez également définir l'opération reset_sample_state, qui réinitialise l'état de la cellule et l'état masqué. Vous devez exécuter cette opération au début, chaque fois que vous faites une séquence de prédictions.
print('Defining prediction related TF functions')
sample_inputs = tf.placeholder(tf.float32, shape=[1,D])
# Maintaining LSTM state for prediction stage
sample_c, sample_h, initial_sample_state = [],[],[]
for li in range(n_layers):
sample_c.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
sample_h.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
initial_sample_state.append(tf.contrib.rnn.LSTMStateTuple(sample_c[li],sample_h[li]))
reset_sample_states = tf.group(*[tf.assign(sample_c[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)],
*[tf.assign(sample_h[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)])
sample_outputs, sample_state = tf.nn.dynamic_rnn(multi_cell, tf.expand_dims(sample_inputs,0),
initial_state=tuple(initial_sample_state),
time_major = True,
dtype=tf.float32)
with tf.control_dependencies([tf.assign(sample_c[li],sample_state[li][0]) for li in range(n_layers)]+
[tf.assign(sample_h[li],sample_state[li][1]) for li in range(n_layers)]):
sample_prediction = tf.nn.xw_plus_b(tf.reshape(sample_outputs,[1,-1]), w, b)
print('\tAll done')
Defining prediction related TF functions
All done
Exécution de la LSTM
Ici, vous vous entraînerez et prédirez les mouvements des prix des actions pour plusieurs époques et vous verrez si les prédictions s'améliorent ou se détériorent avec le temps. Vous suivez la procédure suivante.
- Définir un ensemble de points de départ (
test_points_seq) sur la série temporelle pour évaluer le modèle. - Pour chaque époque
- Pour une séquence complète de données d'apprentissage
- Déroulez un ensemble de lots
num_unrollings - Entraînez le réseau neuronal avec les lots déroulés
- Déroulez un ensemble de lots
- Calculer la perte moyenne de formation
- Pour chaque point de départ de l'ensemble de test
- Mettez à jour l'état de la LSTM en parcourant les points de données
num_unrollingstrouvés avant le point de test. - Faites des prédictions pour les étapes
n_predict_onceen continu, en utilisant la prédiction précédente comme entrée actuelle. - Calculez la perte MSE entre les points
n_predict_onceprédits et les prix réels des actions à ces moments-là.
- Mettez à jour l'état de la LSTM en parcourant les points de données
- Pour une séquence complète de données d'apprentissage
epochs = 30
valid_summary = 1 # Interval you make test predictions
n_predict_once = 50 # Number of steps you continously predict for
train_seq_length = train_data.size # Full length of the training data
train_mse_ot = [] # Accumulate Train losses
test_mse_ot = [] # Accumulate Test loss
predictions_over_time = [] # Accumulate predictions
session = tf.InteractiveSession()
tf.global_variables_initializer().run()
# Used for decaying learning rate
loss_nondecrease_count = 0
loss_nondecrease_threshold = 2 # If the test error hasn't increased in this many steps, decrease learning rate
print('Initialized')
average_loss = 0
# Define data generator
data_gen = DataGeneratorSeq(train_data,batch_size,num_unrollings)
x_axis_seq = []
# Points you start your test predictions from
test_points_seq = np.arange(11000,12000,50).tolist()
for ep in range(epochs):
# ========================= Training =====================================
for step in range(train_seq_length//batch_size):
u_data, u_labels = data_gen.unroll_batches()
feed_dict = {}
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
feed_dict[train_inputs[ui]] = dat.reshape(-1,1)
feed_dict[train_outputs[ui]] = lbl.reshape(-1,1)
feed_dict.update({tf_learning_rate: 0.0001, tf_min_learning_rate:0.000001})
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
average_loss += l
# ============================ Validation ==============================
if (ep+1) % valid_summary == 0:
average_loss = average_loss/(valid_summary*(train_seq_length//batch_size))
# The average loss
if (ep+1)%valid_summary==0:
print('Average loss at step %d: %f' % (ep+1, average_loss))
train_mse_ot.append(average_loss)
average_loss = 0 # reset loss
predictions_seq = []
mse_test_loss_seq = []
# ===================== Updating State and Making Predicitons ========================
for w_i in test_points_seq:
mse_test_loss = 0.0
our_predictions = []
if (ep+1)-valid_summary==0:
# Only calculate x_axis values in the first validation epoch
x_axis=[]
# Feed in the recent past behavior of stock prices
# to make predictions from that point onwards
for tr_i in range(w_i-num_unrollings+1,w_i-1):
current_price = all_mid_data[tr_i]
feed_dict[sample_inputs] = np.array(current_price).reshape(1,1)
_ = session.run(sample_prediction,feed_dict=feed_dict)
feed_dict = {}
current_price = all_mid_data[w_i-1]
feed_dict[sample_inputs] = np.array(current_price).reshape(1,1)
# Make predictions for this many steps
# Each prediction uses previous prediciton as it's current input
for pred_i in range(n_predict_once):
pred = session.run(sample_prediction,feed_dict=feed_dict)
our_predictions.append(np.asscalar(pred))
feed_dict[sample_inputs] = np.asarray(pred).reshape(-1,1)
if (ep+1)-valid_summary==0:
# Only calculate x_axis values in the first validation epoch
x_axis.append(w_i+pred_i)
mse_test_loss += 0.5*(pred-all_mid_data[w_i+pred_i])**2
session.run(reset_sample_states)
predictions_seq.append(np.array(our_predictions))
mse_test_loss /= n_predict_once
mse_test_loss_seq.append(mse_test_loss)
if (ep+1)-valid_summary==0:
x_axis_seq.append(x_axis)
current_test_mse = np.mean(mse_test_loss_seq)
# Learning rate decay logic
if len(test_mse_ot)>0 and current_test_mse > min(test_mse_ot):
loss_nondecrease_count += 1
else:
loss_nondecrease_count = 0
if loss_nondecrease_count > loss_nondecrease_threshold :
session.run(inc_gstep)
loss_nondecrease_count = 0
print('\tDecreasing learning rate by 0.5')
test_mse_ot.append(current_test_mse)
print('\tTest MSE: %.5f'%np.mean(mse_test_loss_seq))
predictions_over_time.append(predictions_seq)
print('\tFinished Predictions')
Initialized
Average loss at step 1: 1.703350
Test MSE: 0.00318
Finished Predictions
...
...
...
Average loss at step 30: 0.033753
Test MSE: 0.00243
Finished Predictions
Visualiser les prévisions
Vous pouvez constater que la perte de MSE diminue avec la quantité d'entraînement. C'est un bon signe que le modèle apprend quelque chose d'utile. Pour quantifier vos résultats, vous pouvez comparer la perte d'EQM du réseau à la perte d'EQM obtenue lors du calcul de la moyenne standard (0,004). Vous pouvez constater que la LSTM fait mieux que la moyenne standard. Et vous savez que la moyenne standard (même si elle n'est pas parfaite) a suivi raisonnablement les véritables mouvements des prix des actions.
best_prediction_epoch = 28 # replace this with the epoch that you got the best results when running the plotting code
plt.figure(figsize = (18,18))
plt.subplot(2,1,1)
plt.plot(range(df.shape[0]),all_mid_data,color='b')
# Plotting how the predictions change over time
# Plot older predictions with low alpha and newer predictions with high alpha
start_alpha = 0.25
alpha = np.arange(start_alpha,1.1,(1.0-start_alpha)/len(predictions_over_time[::3]))
for p_i,p in enumerate(predictions_over_time[::3]):
for xval,yval in zip(x_axis_seq,p):
plt.plot(xval,yval,color='r',alpha=alpha[p_i])
plt.title('Evolution of Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.subplot(2,1,2)
# Predicting the best test prediction you got
plt.plot(range(df.shape[0]),all_mid_data,color='b')
for xval,yval in zip(x_axis_seq,predictions_over_time[best_prediction_epoch]):
plt.plot(xval,yval,color='r')
plt.title('Best Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.show()
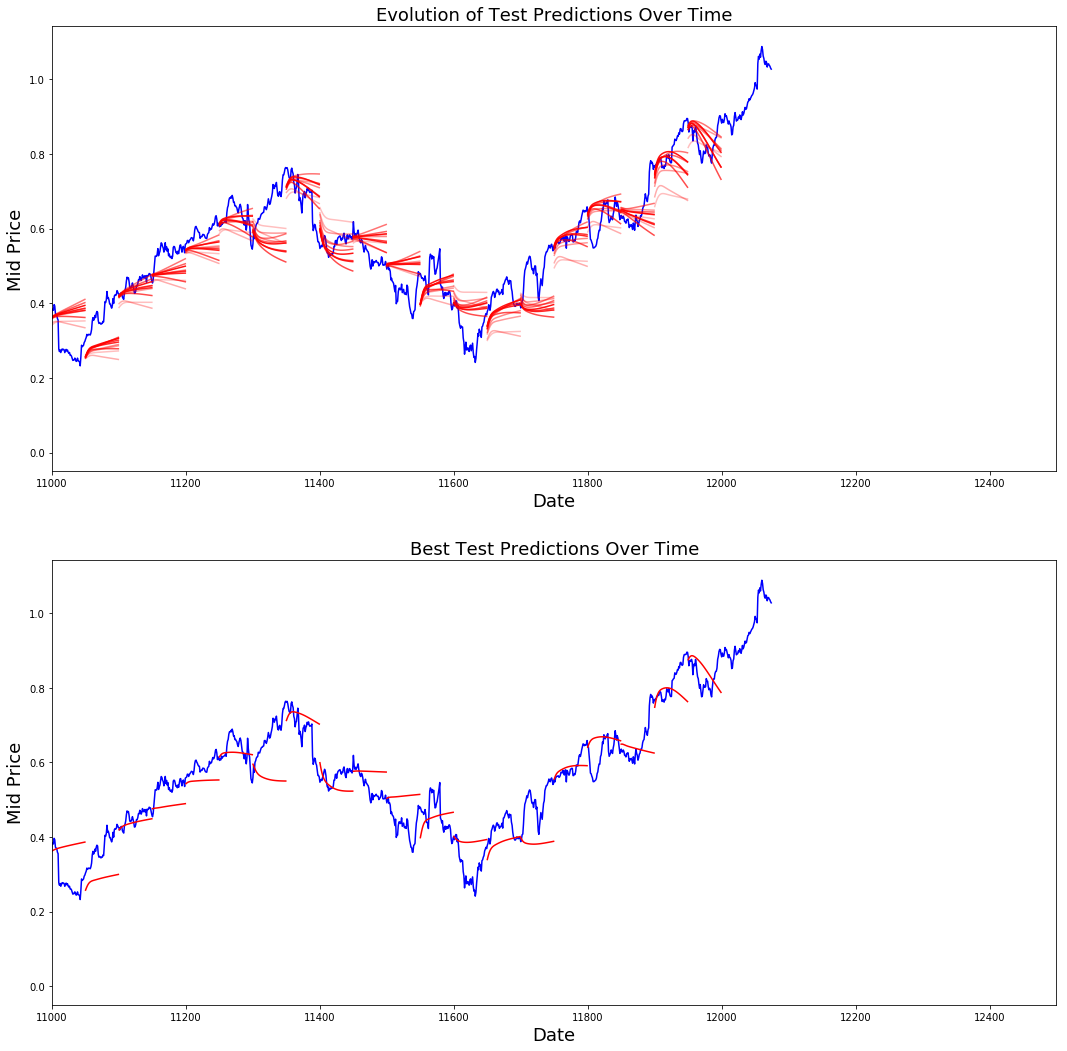
Bien qu'elles ne soient pas parfaites, les LSTM semblent être en mesure de prédire correctement l'évolution du cours des actions la plupart du temps. Notez que vous faites des prédictions approximativement comprises entre 0 et 1,0 (c'est-à-dire pas les prix réels des actions). Ce n'est pas grave, car vous prédisez l'évolution du cours des actions, et non les cours eux-mêmes.
Remarques finales
J'espère que ce tutoriel vous a été utile. Je dois préciser que cette expérience a été enrichissante pour moi. Dans ce tutoriel, j'ai appris à quel point il peut être difficile de mettre au point un modèle capable de prédire correctement les mouvements des cours boursiers. Vous avez commencé par expliquer pourquoi vous devez modéliser les cours des actions. Une explication et un code pour le téléchargement des données ont ensuite été fournis. Vous avez ensuite étudié deux techniques de calcul de la moyenne qui vous permettent de faire des prédictions un peu plus loin dans l'avenir. Vous avez ensuite vu que ces méthodes sont futiles lorsque vous devez prévoir plus d'un pas dans l'avenir. Ensuite, vous avez expliqué comment vous pouvez utiliser les LSTM pour faire des prédictions plusieurs fois dans le futur. Enfin, vous avez visualisé les résultats et constaté que votre modèle (même s'il n'est pas parfait) est tout à fait capable de prédire correctement l'évolution du cours des actions.
Si vous souhaitez en savoir plus sur le deep learning, ne manquez pas de jeter un œil à notre cours Deep Learning in Python. Il couvre les bases, ainsi que la façon de construire un réseau neuronal par vous-même dans Keras. Il s'agit d'un package différent de TensorFlow, qui sera utilisé dans ce tutoriel, mais l'idée est la même.
J'énonce ici plusieurs enseignements tirés de ce tutoriel.
-
La prévision des prix et des mouvements des actions est une tâche extrêmement difficile. Personnellement, je ne pense pas qu'il faille prendre pour acquis les modèles de prévision boursière existants et s'y fier aveuglément. Cependant, les modèles peuvent être en mesure de prédire correctement l'évolution du cours des actions la plupart du temps, mais pas toujours.
-
Ne vous laissez pas abuser par les articles qui montrent des courbes de prédiction qui se superposent parfaitement aux prix réels des actions. Cette situation peut être reproduite à l'aide d'une simple technique de calcul de la moyenne et, dans la pratique, elle est inutile. Il est plus judicieux de prévoir l'évolution du cours des actions.
-
Les hyperparamètres du modèle sont extrêmement sensibles aux résultats que vous obtenez. Une très bonne chose à faire serait donc d'utiliser une technique d'optimisation des hyperparamètres (par exemple, Grid search / Random search) sur les hyperparamètres. Vous trouverez ci-dessous une liste des hyperparamètres les plus critiques.
- Le taux d'apprentissage de l'optimiseur
- Nombre de couches et nombre d'unités cachées dans chaque couche
- L'optimiseur. J'ai trouvé qu'Adam était le meilleur
- Type de modèle. Vous pouvez essayer GRU/ LSTM standard/ LSTM avec Peepholes et évaluer la différence de performance.
-
Dans ce tutoriel, vous avez commis une erreur (due à la petite taille des données) ! En d'autres termes, vous avez utilisé la perte de test pour diminuer le taux d'apprentissage. Les informations relatives à l'ensemble de tests sont ainsi indirectement transmises à la procédure d'apprentissage. Une meilleure solution consiste à disposer d'un ensemble de validation distinct (séparé de l'ensemble de test) et à diminuer le taux d'apprentissage en fonction des performances de l'ensemble de validation.
Si vous souhaitez me contacter, vous pouvez m'envoyer un courriel à l'adresse thushv@gmail.com ou vous connecter avec moi sur LinkedIn.
Références
Je me suis référé à ce référentiel pour comprendre comment utiliser les LSTMs pour les prédictions boursières. Mais les détails peuvent être très différents de la mise en œuvre trouvée dans la référence.
