Curso
Comprender la ciencia de datos
2 h
803.2K
¿Alguna vez te has preguntado por qué unos pocos sitios web reciben la mayor parte del tráfico de Internet? ¿O por qué una pequeña fracción de individuos controla la mayor parte de la riqueza mundial? La respuesta se encuentra en un fascinante fenómeno estadístico conocido como ley de potencias.
Las leyes de potencia rigen muchos sistemas naturales y artificiales. Estas distribuciones son especiales porque no cambian con la escala y tienen colas pesadas. Estas características los hacen perfectos para modelar datos en los que se producen muchos eventos pequeños, pero en los que no se pueden ignorar los eventos grandes e importantes, aunque sean poco frecuentes.
Este tutorial te proporcionará una visión general completa de las leyes de potencias, incluyendo su teoría, matemáticas, usos y cómo estimarlas. Veremos cómo son invariantes en escala y por qué aparecen en campos tan diversos como la geofísica, las finanzas, la biología e Internet.
Propiedades de las distribuciones de ley de potencias
Comencemos por lo que hace especiales a las leyes de potencias y en qué se diferencian de las distribuciones que quizá hayas utilizado hasta ahora.
Características de las leyes de potencia. Fuente: Servilleta AI
Invarianza de escala y autosimilaridad
En pocas palabras, la invariancia de escala implica que, si amplías o reduces la imagen, el patrón de la distribución permanece igual.
En términos estadísticos, una distribución de ley de potencias tiene la misma forma funcional independientemente de la escala en la que se observe. Si una variable sigue una ley de potencias, multiplicarla por una constante no cambia su distribución, solo cambia la escala.
Matemáticamente, esto significa:
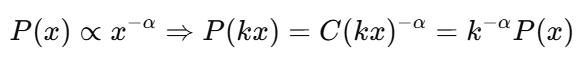
Esto difiere mucho de otras distribuciones comunes, como la distribución normal, en la que laforma se define en función de determinados parámetros clave, como la media y la desviación estándar.
Esta propiedad también es similar a la autosimilaridad, que es un atributo clave de los fractales. Los fractales son estructuras que tienen el mismo aspecto independientemente de cuánto se amplíen. Por ejemplo, si amplías cualquier parte de un copo de nieve, una hoja de helecho o una rama de árbol, verás una versión más pequeña del conjunto.
Una costa se ve igual desde 10 metros de distancia que desde 10 kilómetros.
Las leyes de potencia muestran muy bien esta estructura repetitiva. Por eso son útiles cuando se analizan sistemas en los que el tamaño, la frecuencia o la intensidad varían mucho, pero siempre siguen el mismo patrón.
Colas pesadas y falta de escala característica
La mayoría de las distribuciones clásicas (como la gaussiana o la exponencial) disminuyen rápidamente en los extremos. No es así con las leyes de potencia. Tienencolas pesadas de tipo « », lo que significa que la probabilidad de que se produzcan eventos extremos es mayor.
En la vida real, los grandes terremotos, los tuits virales y los multimillonarios son ejemplos de acontecimientos poco frecuentes que, sin embargo, pueden llegar a ocurrir. De hecho, para algunos valores de alfa, es posible que ni siquiera existan momentos como la media o la varianza, y por eso decimos que las distribuciones de ley de potencias no tienen escala.
Universalidad e incompletitud estadística
Una cosa sorprendente de las leyes de potencia es que son universales; se pueden encontrar en sistemas que no parecen tener ninguna correlación entre sí. Algunos de estos ejemplos incluyen: magnitudes de terremotos, picos en la actividad neuronal, tamaño de las empresas y frecuencias de palabras.
La otra cara de la moneda es que también son estadísticamente incompletos. Esto significa que, aunque podemos modelar cómo se comporta la cola, es difícil estimar un conjunto completo de estadísticas resumidas, especialmente a partir de muestras de datos pequeñas.
Fundamentos matemáticos de las leyes de potencias
Profundicemos en las matemáticas que hacen que las leyes de potencias sean tan poderosas y complicadas.
Forma funcional y propiedades de escalado
La forma estándar de una ley de potencias es:
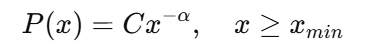
Dónde:
- alfa es el exponente de escala
- C es la constante normalizadora
- xmin es elumbral e e por encima del cual se cumple la ley de potencias.
A medida que aumenta el valor alfa, la cola se vuelve más delgada. Un alfa pequeño significa que los eventos son más extremos. Este exponente de escala rige todo, desde la desigualdad hasta el tamaño de los ecosistemas.
Distribuciones de probabilidad de ley de potencias y gráficos logarítmicos
El primer paso es utilizar un gráfico logarítmico para detectar una ley de potencias en conjuntos de datos reales.
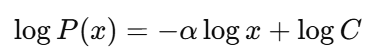
Si los datos realmente siguen una ley de potencias, obtendrás una línea recta con una pendiente de −α. Pero ten cuidado, ya que muchas distribuciones parecen lineales en un gráfico logarítmico.
Relaciones con otras distribuciones
Existen varias distribuciones estadísticas importantes que son similares a las leyes de potencias.
- Las distribuciones de Pareto, que se utilizan a menudo en economía, muestran la distribución de la riqueza y los ingresos, donde un pequeño número de personas posee la mayor parte de los recursos. Este es un ejemplo temprano y clásico de una ley de potencias en acción.
- La ley de Zipf explica cómo las frecuencias de las palabras en el lenguaje natural siguen un patrón de ley de potencias. Por ejemplo, la segunda palabra más común aparece aproximadamente la mitad de veces que la palabra más común, la tercera aproximadamente un tercio, y así sucesivamente.
- La distribución zeta es una versión discreta de la ley de potencias que se utiliza a menudo para modelar cosas que ocurren con frecuencia, como las visitas a un sitio web o las ventas de libros.
A veces, los datos del mundo real no siguen una ley de potencia «pura» para siempre. En estas situaciones, observamos cortes exponenciales (donde los valores muy grandes se vuelven menos probables), leyes de potencia curvas o colas log-normales. Son mejores para modelar sistemas con límites físicos o prácticos. Estos híbridos saben que la invarianza de escala puede funcionar para parte del rango, pero que al final dejará de hacerlo.
Manifestaciones empíricas en diversas disciplinas
Las leyes de potencia no son solo ideas matemáticas; aparecen en el mundo real y nos ayudan a comprender sistemas que, en un primer momento, parecen aleatorios o caóticos.
Sistemas naturales y geofísicos
Las leyes de potencias nos ayudan a comprender los fenómenos extremos de la naturaleza. Por ejemplo, la ley de Gutenberg-Richter establece que la magnitud de los terremotos sigue una distribución de ley de potencias. Esto significa que se producen muchos temblores pequeños, pero a medida que aumenta la magnitud del terremoto, el número de temblores disminuye rápidamente. Por eso, puede ocurrir un terremoto de magnitud 2,0 todos los días, pero puede que no ocurra ninguno de magnitud 7,0 en años. Ambos forman parte de la misma historia estadística.
Del mismo modo, las redes fluviales, las costas e incluso los rayos muestran patrones fractales autosimilares que siguen una ley de escalado de potencias en el tamaño de sus segmentos.
Las leyes de potencia también son aplicables al universo. En astrofísica, vemos que el tamaño de las estrellas, la distribución de los agujeros negros e incluso los cúmulos de galaxias tienen colas pesadas. Hay miles de millones de estrellas pequeñas, pero solo unas pocas enormes destacan en la galaxia. Puede parecer que esta irregularidad es aleatoria, pero una vez que comprendemos la ley de potencias que subyace bajo la superficie, podemos ver que sigue ciertas reglas estadísticas.
Sistemas socioeconómicos y biológicos
Cuando se analiza la desigualdad y la escala en las sociedades humanas, las leyes de potencia resultan especialmente útiles. Ya hemos hablado de la distribución de Pareto en la sección anterior, que no es solo una teoría sobre la economía, sino que se puede observar en los registros fiscales, los beneficios empresariales y los patrones de donaciones.
El 1 % de las personas más ricas siguen la ley de Pareto, no los promedios gaussianos. Estas distribuciones no encajan en una curva de campana perfecta, sino que se extienden hacia la derecha, mostrando unos pocos valores extremos (como los multimillonarios) que desequilibran la media.
Las leyes de potencia también muestran patrones ocultos en la biología. Por ejemplo, la ley de Kleiber dice que la tasa metabólica de un animal aumenta a medida que su masa corporal aumenta a la potencia de 3/4, y no en línea recta. Esto nos ayuda a comprender por qué un elefante no come mil veces más que un conejo, aunque pesa mil veces más.
Las leyes de potencia también se aplican a la población de las ciudades, las tasas de crecimiento de las empresas, el comportamiento electoral e incluso las muertes en conflictos, donde unos pocos elementos o acontecimientos importantes tienen un efecto desproporcionado.
Tecnología y negocios
Las leyes de potencia son las que mantienen el mundo digital en funcionamiento y lo hacen prosperar. Piensa en cómo funciona el tráfico en Internet: solo unos pocos sitios web (como Google, Facebook y YouTube) reciben la mayor parte de las visitas, mientras que millones de otras páginas pasan prácticamente desapercibidas. Este es un comportamiento típico de la larga cola, y es especialmente importante en áreas como el SEO, los motores de recomendación y el marketing digital.
En IA, el tamaño y el rendimiento de los modelos tienden a ir en la misma dirección. Hay algunos modelos grandes, como GPT-4, que son los mejores en este campo, pero cientos de modelos más pequeños no pueden seguirles el ritmo. Esta concentración se debe en parte a los bucles de retroalimentación: los mejores modelos obtienen más usuarios, datos y dinero, lo que los hace aún más poderosos.
Estimación estadística y validación
Por lo tanto, parece que tu conjunto de datos sigue una ley de potencias. El histograma podría tener una cola larga, o el gráfico logarítmico podría mostrar una línea casi recta. Es un buen comienzo, pero no basta con mirarlo, ya que no es difícil dejarse engañar por las leyes de potencia. Por eso necesitamos buenas herramientas estadísticas para determinar los parámetros y comprobar el ajuste.
Métodos de estimación de parámetros
El exponente de escala, que normalmente se escribe como 𝛼, es lo primero que necesitas para modelar correctamente una distribución de ley de potencias.
La estimación de máxima verosimilitud (MLE) es una de las formas más comunes de obtener una estimación de 𝛼. Es una forma de encontrar los valores de los parámetros que hacen que los datos observados sean los más probables en todas las estadísticas.
Para datos continuos con un valor mínimo conocido 𝑥min, así es como funciona:
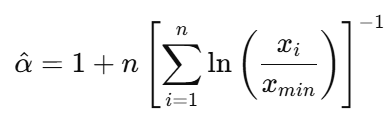
- 𝑥𝑖 son los valores que has visto, y todos son mayores o iguales que 𝑥𝑚𝑖𝑛.
- 𝑛 es el número de observaciones.
Pero aquí está lo difícil: elegir el 𝑥 min adecuado es muy importante. Si es demasiado bajo, tu modelo tiene datos que realmente no siguen la ley de potencias. Y si es demasiado alto, acabarás gastando demasiados datos. Además, cuando el tamaño de las muestras es pequeño, las estimaciones MLE pueden ser poco fiables.
Prueba de bondad de ajuste
Después de estimar el exponente, la siguiente pregunta es: ¿qué tan bien encaja? No puedes limitarte a decir: «Parece una ley de potencias». Necesitas pruebas estadísticas de que la ley de potencias explica mejor tus datos que otras distribuciones posibles. Aquí es donde entra en juego la pruebade Kolmogorov-Smirnov (KS). Esta prueba encuentra la mayor diferencia entre la función de distribución acumulativa (CDF) de los datos observados y el modelo teórico de ley de potencias.
Cuanto más se acerque este número a cero, mejor se ajustará tu modelo a los datos. La prueba KS no utiliza agrupaciones ni histogramas como muchas otras pruebas. En su lugar, trabaja directamente con los datos brutos, lo que lo hace muy útil para distribuciones de cola pesada.Pero a veces, una ley de potencias no es la única explicación plausible. Una distribución log-normal o exponencial también podría modelar tus datos. Es aquí donde resultan útileslas pruebas de razón de verosimilitud de . La idea es sencilla: utiliza MLE para ajustar ambos modelos a los mismos datos, encuentra las probabilidades y, a continuación, compáralas. Tienes respaldo estadístico para el modelo de ley de potencias si su probabilidad es mucho mayor.
El marco de Clauset-Shalizi-Newman (2009) es una de las muchas herramientas que combinan el MLE, las pruebas KS y las pruebas de razón de verosimilitud en una forma sólida de analizar el comportamiento de la ley de potencias.
Mecanismos teóricos y modelos generativos
Ahora que sabemos dónde aparecen las leyes de potencias en el mundo real y cómo encontrarlas estadísticamente, la siguiente pregunta es: ¿por qué aparecen estas distribuciones en primer lugar? Veamos cómo pueden surgir las leyes de potencia a partir de la dinámica de sistemas.
Adhesión preferencial y procesos de Yule
El modelo Barabási-Albert (1999) introdujo el apego preferencial, que a menudo se resume como el fenómeno de «los ricos se hacen más ricos». Es una de las formas más conocidas y fáciles de entender cómo funcionan las leyes de potencias.
Piensa en crear una red, como Internet o una red social. Cuando se une un nuevo usuario, es más probable que se conecte a nodos populares como Facebook o Google, ya que esos nodos ya son conocidos.
Con el tiempo, esto crea un bucle de retroalimentación: los nodos populares obtienen aún más conexiones, mientras que los más nuevos o menos conectados permanecen pequeños. Esto crea una red sin escala en la que los grados de los nodos siguen una ley de potencias.
De manera similar, los procesos de Yule modelan el crecimiento de los géneros biológicos, lo cual es una extensión de esta idea. En este modelo, las especies que ya tienen más miembros son más propensas a dar lugar a nuevas especies. Esto conduce a una distribución sesgada en la que unos pocos géneros son los que predominan.
Modelos de crecimiento aleatorio, ley de Gibrat y procesos de Markov
Los procesos de crecimiento aleatorio son otra forma en que pueden manifestarse las leyes de potencia. La idea principal es que las cosas se hacen más grandes con el tiempo multiplicando cantidades aleatorias en lugar de sumarlas.
La ley de Gibrat establece que la tasa de crecimiento es independiente del tamaño. La mayoría de las cosas permanecen pequeñas, pero unas pocas crecen muy rápido y se hacen muy grandes, formando la cola pesada de una ley de potencias.
Los procesos de Markov, especialmente aquellos que implican ruido multiplicativo, también pueden converger hacia distribuciones estacionarias similares a la ley de potencias, especialmente bajo límites reflectantes.
También hay un aspecto probabilístico en esto. Los procesos de Markov también pueden mostrar un comportamiento de ley de potencias en algunas situaciones. Estos procesos modelan sistemas en los que el estado siguiente solo depende del estado actual, no del pasado. La gente ha utilizado esto para modelar cosas como el movimiento de las personas en una población y el funcionamiento de las colas.
Estos modelos no son solo ideas interesantes. Nos ayudan a comprender cómo cambian los sistemas complejos a lo largo del tiempo, por qué se mantiene la desigualdad y cómo los efectos de red afectan a todo, desde la biología hasta la cadena de bloques. No solo podemos usar las leyes de potencia para describir el mundo, sino que también podemos usarlas para explicarlo.
Implicaciones, limitaciones y aplicaciones
Comprender la dinámica de las leyes de potencia es fundamental y puede tener un gran impacto en tus predicciones y decisiones, ya sea que estés elaborando un modelo de riesgo financiero, gestionando una infraestructura de Internet o estudiando el comportamiento social.
Consideraciones prácticas
Los modelos de ley de potencias son útiles para sistemas en los que se producen acontecimientos poco frecuentes pero importantes. Por ejemplo, en finanzas, los precios pueden variar a un ritmo normal la mayoría de los días, pero los «cisnes negros» —las raras caídas o subidas— pueden tener el mayor efecto.
Los modelos de ley de potencias pueden captar mejor este riesgo extremo que los modelos tradicionales, que a menudo subestiman la probabilidad de que se produzcan estos eventos. Para la gestión de riesgos, los seguros, la ciberseguridad y la planificación ante desastres, eso es muy importante.
También existe la ventaja de comprender el crecimiento no lineal y los efectos compuestos. Las leyes de potencia ayudan a explicar por qué algunas personas, empresas o nodos de una red pueden llegar a ser los más poderosos con el tiempo y por qué estas situaciones en las que «el ganador se lo lleva todo» no son solo inusuales, sino normales en este tipo de sistemas.
Sin embargo, los modelos de ley de potencias tienen algunas desventajas. Un problema es que desafían la intuición, ya que no siempre tienen medias o varianzas claras, lo que dificulta calcular métricas comunes como el «valor esperado» o la «desviación estándar».
Estos modelos suelen funcionar solo en la cola de la distribución, por lo que es posible que no se ajusten bien o que no se ajusten en absoluto a la mayor parte de los datos. Esto puede ser un problema si no se tiene cuidado con el punto en el que realmente comienza el comportamiento de la ley de potencias.
Limitaciones y críticas
No todos los conjuntos de datos con colas largas siguen una ley de potencias real. Pocas distribuciones, como la log-normal o la exponencial estirada, pueden parecer un comportamiento de ley de potencias en un rango pequeño, especialmente en un gráfico logarítmico. Esto a menudo conduce a falsos positivos, en los que tomamos como ley de potencias solo porque el gráfico «parece lineal».La generalización excesiva es otro problema. A menudo se piensa que las leyes de potencia explican todo lo que ocurre en un sistema, pero es posible que solo expliquen una pequeña parte, normalmente los extremos. Por ejemplo, el 1 % de las personas con mayores ingresos puede tener una distribución de ingresos que sigue una ley de potencias, pero el resto de la población puede tener una distribución muy diferente.
La ley de los rendimientos decrecientes es otro problema al que se enfrentan los sistemas del mundo real. Las leyes de potencia establecen que son posibles resultados extremos, pero en algunas áreas, como los límites físicos o los entornos normativos, existen límites más allá de los cuales el modelo deja de funcionar. Si crees que el comportamiento de la cola continúa indefinidamente, es posible que pienses que los riesgos o las recompensas son mayores de lo que realmente son, especialmente en sistemas con límites.
Conclusión
Las leyes de potencia nos ayudan a comprender sistemas en los que unos pocos eventos o entidades extremos tienen un gran efecto, como los terremotos, el tráfico de Internet o la distribución de los ingresos. En este tutorial, hemos aprendido qué diferencia a las leyes de potencias, sus propiedades matemáticas y huellas empíricas, cómo encontrarlas y verificarlas, y dónde se pueden encontrar en el mundo real.
El análisis de la ley de potencias tendrá interesantes aplicaciones futuras en áreas como la inteligencia artificial, la economía, la ciencia de redes y la gestión de riesgos. Podemos utilizarlos para comprender mejor un mundo complejo y no lineal si contamos con las herramientas y los conocimientos adecuados.
A medida que profundizas en los datos del mundo real, pregúntate siempre: ¿lo raro es realmente raro, o simplemente está muy distribuido?
Si deseas obtener más información sobre algunos de los conceptos, consulta los siguientes recursos:
¿Qué es una distribución de ley de potencias en términos sencillos?
¿Cómo puedo saber si mis datos siguen una ley de potencias?
¿Qué significa realmente «invarianza de escala»?
¿Dónde aparecen las leyes de potencia en la vida real?
¿Pueden las leyes de potencia modelar todo el conjunto de datos?
Temas
