Comprender la Distribución de Pareto: Guía completa

¿Alguna vez has organizado una fiesta de pizza y te has dado cuenta de algo interesante? Desde luego que sí. En mi última reunión, observé que mientras la mayoría de la gente cogía uno o dos trozos, un puñado de invitados devoraba casi la mitad de las pizzas. Mientras observaba cómo se desarrollaba esto, me llamó la atención: Estaba presenciando un ejemplo real de uno de los patrones más fascinantes de la ciencia de datos: la distribución de Pareto.

Me encanta este ejemplo porque capta perfectamente de qué trata la distribución de Pareto: la observación de que, en muchas situaciones, un pequeño grupo representa una gran parte del resultado.

Como científico de datos, he llegado a apreciar cómo esta distribución nos ayuda a comprender y modelar situaciones en las que "los pocos vitales" dominan a "los muchos triviales". Piensa en ello: El 20% de los clientes de una empresa suelen generar el 80% de sus ingresos, o el 20% del contenido de un sitio web puede generar el 80% de su tráfico. Este patrón es tan común que se conoce como principio de Pareto o "regla 80/20", aunque las proporciones exactas pueden variar.

Pero esto es lo que hace que la Distribución de Pareto sea realmente especial: no es sólo una observación casual, sino una poderosa herramienta matemática que nos ayuda a modelar y predecir estos patrones desequilibrados en los datos. Tanto si analizas la desigualdad económica, como si optimizas las operaciones empresariales o estudias los fenómenos naturales, comprender la Distribución de Pareto puede aportar valiosas ideas sobre por qué las cosas no siempre están distribuidas uniformemente, y lo que eso significa para nuestro análisis.

La capacidad única de la distribución de Pareto para poner de relieve los desequilibrios la ha hecho indispensable en campos que van desde la economía a las ciencias naturales. Si estás ansioso por explorar patrones estadísticos similares, considera la posibilidad de sumergirte en recursos como Fundamentos de la probabilidad en Python para una base en conceptos de probabilidad, o Distribuciones de probabilidad multivariante en R para ampliar tu conjunto de herramientas analíticas. Para los estudiantes visuales, la chuleta Introducción a las Reglas de la Probabilidad sirve como excelente referencia rápida para los principios clave.

¿Qué es la distribución de Pareto?

Cuando el economista italiano Vilfredo Pareto miró a su jardín en 1896, observó algo peculiar: El 20% de sus vainas contenían el 80% de los guisantes. Esta observación le llevó a explorar pautas similares en la propiedad de la tierra, donde descubrió que el 80% de la tierra de Italia pertenecía al 20% de su población. Lo que empezó como una observación de jardín floreció hasta convertirse en una de las herramientas más versátiles de la estadística para comprender las distribuciones desiguales.

Antecedentes históricos

A finales del siglo XIX, las investigaciones de Vilfredo Pareto fueron mucho más allá de las vainas de guisantes y la propiedad de la tierra. Analizó los patrones de distribución de la riqueza en distintos países y periodos de tiempo, descubriendo una relación matemática coherente. Descubrió que la minoría rica poseía la mayoría de los bienes en todas las sociedades que estudió. Este patrón apareció de forma tan constante que otros investigadores empezaron a aplicar sus ideas a distintos campos, desde la economía a las ciencias naturales.

La distribución ganó prominencia cuando el consultor de gestión Joseph Juran se topó con el trabajo de Pareto en 1937. Juran denominó a este patrón "principio de Pareto" y lo aplicó al control de calidad, demostrando que la mayoría de los defectos de fabricación procedían de un número reducido de causas. Esta aplicación ayudó a transformar la gestión de la calidad industrial y despertó un interés más amplio por las ideas de Pareto.

Características principales 

La distribución de Pareto se distingue de otras distribuciones estadísticas por varias características únicas:

1. Comportamiento de ley de potencia: A diferencia de la curva de campana (distribución normal), en la que los valores extremos se vuelven exponencialmente raros, la distribución de Pareto sigue una ley de potencia. Esto significa que los valores extremos se dan con más frecuencia de lo que cabría esperar.
2. Invarianza de escala: Si te acercas a cualquier parte de una distribución de Pareto, el patrón se parece al conjunto. Esta propiedad, conocida como invariancia de escala, ayuda a explicar por qué la distribución aparece en contextos tan diversos.
3. El principio 80/20: Aunque las cifras exactas pueden variar (puede ser 90/10 o 70/30), la idea central se mantiene: un pequeño porcentaje de causas crea un gran porcentaje de efectos.
4. Cola pesada: La "cola" de la distribución (la parte que representa valores mayores) disminuye más lentamente que las distribuciones exponenciales. Esta propiedad matemática explica por qué los valores extremos -como los multimillonarios en la distribución de la riqueza- se dan con más frecuencia de lo que predeciría una distribución normal.

Estas características hacen que la distribución de Pareto sea especialmente buena para modelizar situaciones en las que los recursos, efectos o resultados se concentran en un pequeño subconjunto de una población.

Formulación matemática de la distribución de Pareto

Desglosemos las matemáticas que hay detrás de la distribución de Pareto en trozos digeribles. Aunque las fórmulas pueden parecer intimidantes al principio, te guiaré paso a paso por cada componente.

Fórmula de la distribución de Pareto

La función de densidad de probabilidad (FDP) de la distribución de Pareto tiene esta forma:

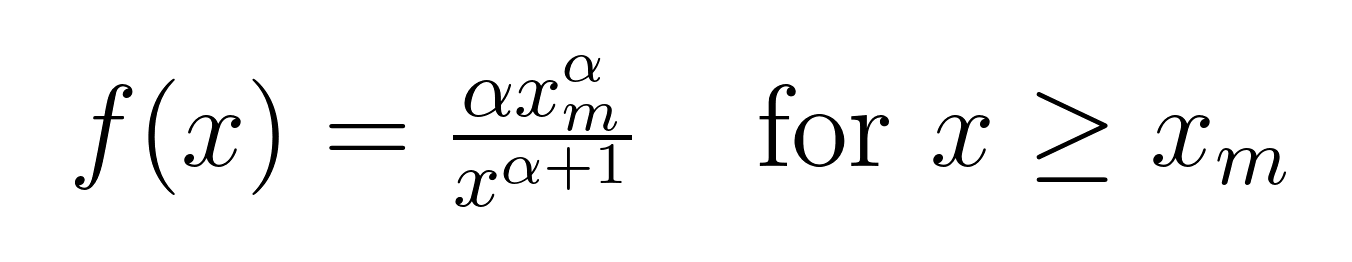
Descifremos qué significa cada símbolo:

• x es nuestra variable aleatoria (como la riqueza, el tamaño de la ciudad o el tráfico del sitio web)
• xₘ es el valor mínimo posible de x (también llamado parámetro de escala)
• α (alfa) es el parámetro de forma que determina la rapidez con que cae la cola

La función de distribución acumulativa (FDA) nos da la probabilidad de que un valor sea menor o igual que x:

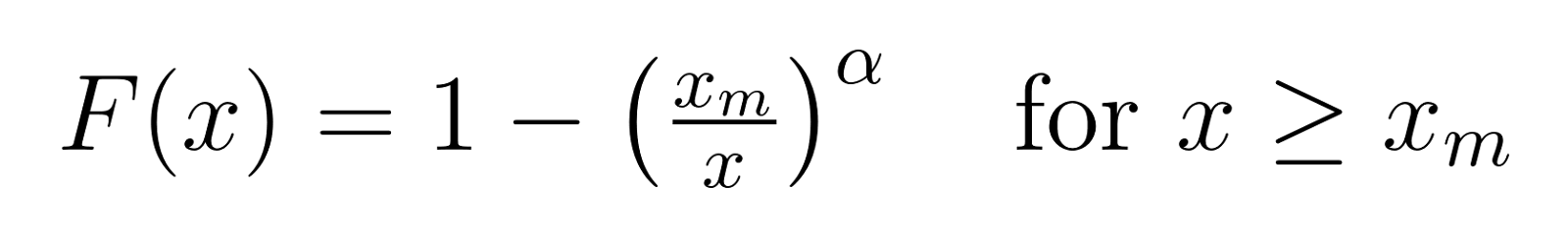
Para concretar estas fórmulas, veamos qué significan los distintos valores de α:

Comprender el principio de Pareto

La famosa regla 80/20 surge naturalmente de la distribución de Pareto cuando α ≈ 1,16.

En el análisis de datos, este principio nos ayuda:

1. Identificar los factores de alto impacto en nuestro conjunto de datos
2. Centrar los recursos en las variables más influyentes
3. Predecir dónde pueden producirse valores extremos
4. Establece expectativas realistas sobre la distribución de los datos

Por ejemplo, al analizar los datos de los clientes, podríamos descubrir que:

• El 20% de los productos genera el 80% de las ventas
• El 20% de las correcciones de errores resuelven el 80% de las quejas de los clientes
• El 20% de las campañas de marketing generan el 80% de las nuevas inscripciones

Estos conocimientos ayudan a las empresas a tomar decisiones informadas sobre dónde centrar sus esfuerzos para obtener el máximo impacto.

Aplicaciones de la distribución de Pareto

Desde las políticas económicas hasta las catástrofes naturales, la distribución de Pareto aparece en lugares sorprendentes.

Economía y distribución de la riqueza

Entra en el distrito financiero de cualquier país y verás la distribución de Pareto en funcionamiento. Los bancos y los economistas lo utilizan para rastrear la concentración de riqueza, modelar las disparidades de ingresos y analizar las políticas fiscales. Por ejemplo, cuando los economistas estudiaron la riqueza mundial en 2023, descubrieron que el 1% de los adultos más ricos poseía el 44% de la riqueza mundial. Esta distribución ayuda a los responsables políticos a comprender las diferencias de riqueza y a diseñar intervenciones económicas. Si te interesan las ideas sobre la distribución de la riqueza, tenemos tutoriales sobre el coeficiente de Gini y la curva de Lorenz.

Empresa y marketing

En los negocios, el principio de Pareto ayuda a las empresas a trabajar de forma más inteligente, no más dura. Piensa en un sitio de comercio electrónico que analiza los datos de sus clientes:

• Segmentación de clientes: Identificar y retener a los clientes VIP que generan más ingresos
• Gestión de inventarios: Centrarse en los productos con mayores ventas y optimizar el almacenamiento
• Asignación de recursos: Dirigir a los equipos de ventas hacia clientes potenciales prometedores y priorizar las características principales

Fenómenos naturales e investigación científica

La naturaleza también sigue patrones de Pareto. Los científicos utilizan esta distribución para estudiar:

• Patrones geográficos: Población de las ciudades, redes fluviales, tamaño de los incendios forestales
• Acontecimientos geológicos: Magnitudes de los terremotos y réplicas
• Sistemas biológicos: Abundancia de especies en los ecosistemas

Por ejemplo, los terremotos: su distribución de magnitud sigue un patrón de Pareto, con muchos temblores pequeños y raros terremotos devastadores. Esta comprensión ayuda a los sismólogos a desarrollar mejores modelos de predicción y evaluaciones de riesgos.

Visualizar la distribución de Pareto

La visualización de datos da vida a las propiedades únicas de la distribución de Pareto. Exploremos el aspecto gráfico de esta distribución y lo que sus formas nos dicen sobre los datos que estamos analizando.

Representación gráfica

La forma más habitual de visualizar la distribución de Pareto es a través de su función de densidad de probabilidad (PDF). Esto nos muestra cómo se distribuyen los valores en nuestro conjunto de datos.

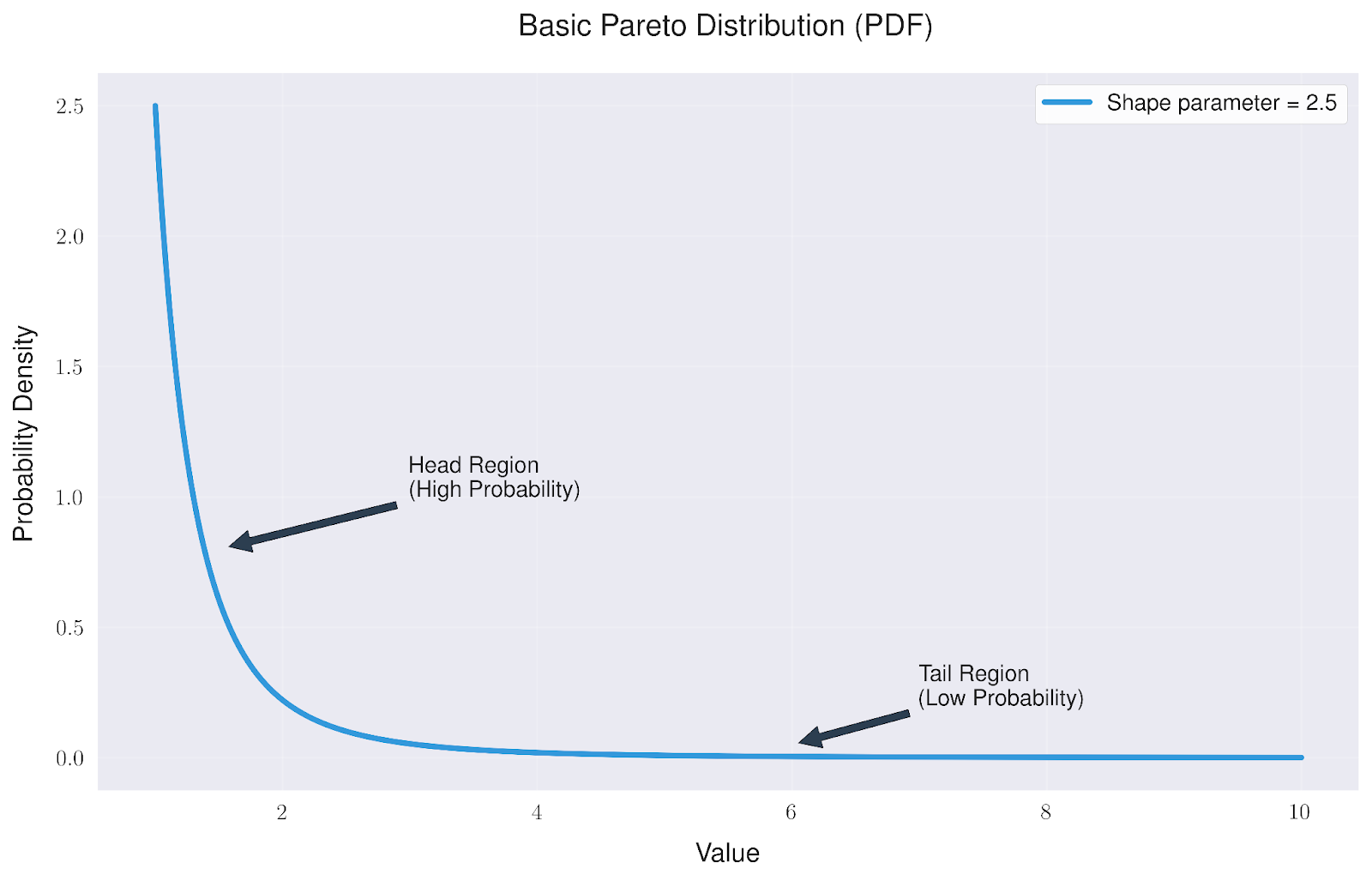
La distribución básica de Pareto tiene una forma característica que nos dice dos cosas importantes:

1. La región de la "cabeza" muestra una alta concentración de probabilidad cerca del valor mínimo
2. La región de la "cola" se extiende mucho hacia la derecha, mostrando que aunque los valores extremos son raros, son más comunes que en muchas otras distribuciones

Lo que hace especialmente interesante a la distribución de Pareto es cómo cambia con distintos parámetros de forma. Estos parámetros influyen directamente en lo extremos que pueden ser nuestros valores.

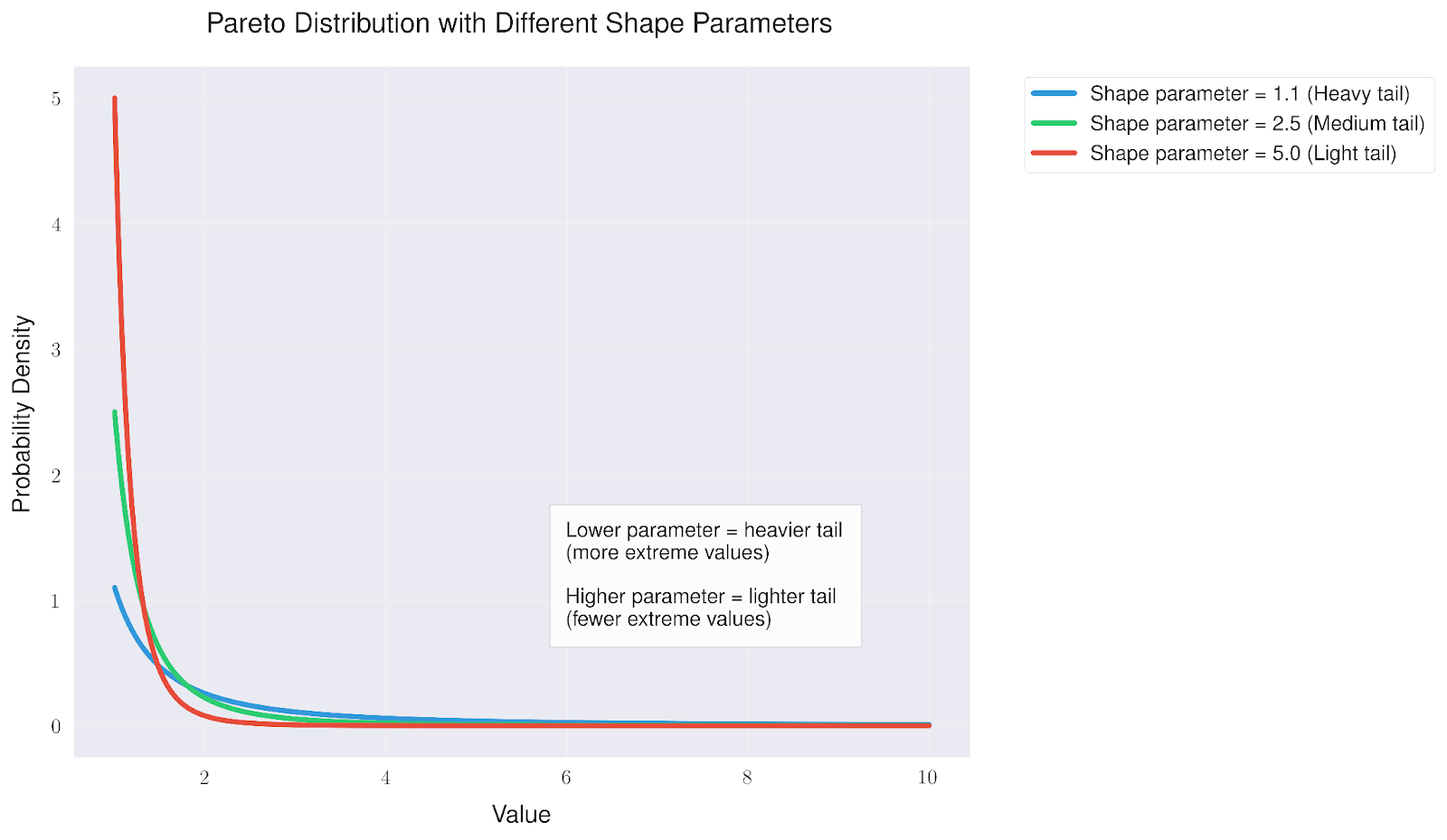
El examen de diferentes parámetros de forma revela que

• Los valores más bajos (como 1,1) crean una "cola pesada" en la que es más probable que se produzcan valores extremos
• Los valores medios (en torno a 2,5) ofrecen un equilibrio entre sucesos comunes y extremos
• Los valores más altos (como 5,0) crean una "cola ligera" en la que los valores extremos son cada vez más raros

Esta flexibilidad hace que la distribución de Pareto sea útil para modelar diversos fenómenos del mundo real, desde la distribución de la riqueza (a menudo de cola pesada) hasta los defectos de fabricación (normalmente de cola más ligera).

La distribución de la riqueza suele tener colas pesadas y esto implica una probabilidad no despreciable de valores extremadamente grandes, por lo que los acontecimientos raros pero masivos (como los multimillonarios) tienen un gran impacto. Esto tiene sentido porque se produce un efecto compuesto, ya que las personas con dinero pueden invertir. Las distribuciones con colas ligeras (como algunos tipos de defectos de fabricación) decaen más rápidamente debido a procesos acotados y estables, lo que significa que los valores extremos son mucho menos probables, ya que las grandes desviaciones son poco frecuentes.

Herramientas de visualización

Para visualizar la distribución de Pareto, nos basamos principalmente en lenguajes de programación estadística y software especializado. Python destaca como una opción popular, ya que ofrece potentes bibliotecas como scipy.stats para realizar cálculos, junto con matplotlib y seaborn para crear visualizaciones claras y con calidad de publicación. R también destaca en este campo, con sus sólidas funciones estadísticas integradas y el versátil paquete ggplot2 para trazar gráficos. 

Aunque Excel es excelente para crear gráficos de Pareto (gráficos de barras que muestran el principio 80/20), no es la mejor herramienta para visualizar y trabajar con la propia distribución de probabilidad de Pareto. Para un análisis estadístico y una visualización adecuados de la distribución de Pareto, te recomendamos que utilices las herramientas de programación mencionadas anteriormente.

Para reforzar tu comprensión de la visualización de las distribuciones de probabilidad, varios recursos pueden servirte como valiosos puntos de partida. El Tutorial de Distribuciones de Probabilidad en Python proporciona experiencia práctica con la implementación de varias distribuciones, incluyendo ejemplos detallados utilizando las bibliotecas estadísticas de Python. Para los interesados en los aspectos visuales, el artículo Visualizaciones de datos que capturan distribuciones cubre técnicas específicamente diseñadas para representar distribuciones estadísticas de forma eficaz. Por último, la Hoja de trucos para la visualización de datos sirve como referencia rápida para elegir y crear visualizaciones adecuadas para distintos tipos de datos distributivos. El conjunto de estos recursos proporciona una buena base tanto para comprender como para visualizar la distribución de Pareto.

Limitaciones y retos de la distribución de Pareto

Toda herramienta estadística tiene sus límites, y la distribución de Pareto no es una excepción. Aunque es una lente poderosa para ver ciertos tipos de datos, saber cuándo no usarla es tan importante como saber cuándo encaja perfectamente. Permíteme compartir algunas consideraciones clave que he aprendido a tener en cuenta cuando trabajo con esta distribución.

Supuestos y limitaciones

Piensa en la distribución de Pareto como en un objetivo de cámara especializado: funciona de maravilla para determinadas tomas, pero puede distorsionar otras. Sus supuestos básicos actúan como las especificaciones técnicas que debemos respetar:

En primer lugar, está el requisito del valor mínimo. A diferencia de otras distribuciones que pueden manejar cualquier número, la distribución de Pareto necesita un punto de partida claro por encima de cero. Es como tener una apuesta mínima en un casino: no puedes jugar con menos de esa cantidad. Esto resulta especialmente complicado cuando tus datos incluyen ceros o valores negativos, como cuando realizas el seguimiento de escenarios de pérdidas y ganancias.

La distribución también supone que cada acontecimiento es independiente de los demás. Pero la vida real rara vez funciona así. Por ejemplo, la acumulación de riqueza: tener dinero a menudo facilita ganar más dinero. Estas interconexiones pueden hacer que la distribución de Pareto sea menos exacta de lo que cabría esperar.

Quizá lo más intrigante sea que la distribución asume la invarianza de escala, es decir, la idea de que las diferencias relativas importan más que las absolutas. Aunque esto suele ser cierto, los escenarios del mundo real a veces se saltan esta regla. El impacto de duplicar la riqueza de alguien, por ejemplo, es muy diferente según el nivel de riqueza.

Interpretaciones erróneas y errores comunes

Según mi experiencia, hay varias trampas en las que pueden caer incluso los analistas experimentados cuando trabajan con la distribución de Pareto. 

La más común es la sobregeneralización. Que veas un patrón similar al 80/20 no significa automáticamente que estés ante una distribución de Pareto. Es como suponer que todos los pájaros que ves son águilas: la forma puede ser similar, pero los detalles importan. Comprueba siempre el ajuste de tu distribución antes de sacar conclusiones.

La estimación de los parámetros presenta otro reto. El parámetro de forma (α) puede ser especialmente sensible a los valores atípicos, sobre todo con conjuntos de datos pequeños. Es como intentar medir la altura media de una población: unos pocos individuos muy altos o muy bajos pueden sesgar significativamente tus resultados si el tamaño de tu muestra es demasiado pequeño.

Cuando se trata de predecir acontecimientos extremos, la cola pesada de la distribución de Pareto puede ser tanto una bendición como una maldición. Aunque es genial para modelar la posibilidad de resultados extremos, a veces puede sugerir que son más probables de lo que realmente son. Esto es especialmente importante en los escenarios de evaluación de riesgos: no querrás sobrestimar ni subestimar los sucesos raros.

Por último, está lo que yo llamo "ceguera contextual": quedarnos tan atrapados en la elegancia matemática de la distribución que nos olvidamos de preguntarnos si tiene sentido para nuestra situación concreta. Recuerda, el mapa no es el territorio, y la distribución de Pareto es sólo un mapa entre muchos.

En caso de duda, considera distribuciones alternativas y valida siempre tus suposiciones con el conocimiento real de tu dominio. Al fin y al cabo, las estadísticas deben estar al servicio de nuestra comprensión de la realidad, y no al revés.

El Principio de Pareto en la vida real

El plan de la naturaleza en la dinámica de los ecosistemas

En los ecosistemas naturales, el principio de Pareto se revela a través del fascinante concepto de especies clave: esos pocos organismos que ejercen una influencia desmesurada sobre su entorno. Considera cómo los lobos de Yellowstone afectan a todo, desde las poblaciones de alces a los patrones fluviales, o cómo los arrecifes de coral, que comprenden sólo una pequeña fracción del espacio oceánico, sustentan casi una cuarta parte de todas las especies marinas. Esta distribución natural 80/20 aparece en todo, desde el tamaño de las copas de los árboles hasta la distribución de las precipitaciones a lo largo de las estaciones.

La sinfonía de la distribución de la riqueza

Piensa en la distribución de la riqueza como en una actuación de orquesta, en la que unos pocos instrumentos clave llevan la melodía principal mientras otros proporcionan un apoyo esencial de fondo. Al igual que la sección del primer violín suele dirigir la orquesta, un pequeño porcentaje de individuos posee la mayor parte de la riqueza mundial, creando una compleja composición económica. Esta pauta tiene profundas implicaciones para la política económica, pues plantea cuestiones sobre cómo mantener tanto el dinamismo que puede impulsar la concentración de riqueza como la armonía social que requiere una participación más amplia. Comprender este paralelismo musical nos ayuda a apreciar tanto la eficacia como los retos de la riqueza concentrada.

La regla de la innovación: cuando menos crea más

En el ámbito de la innovación, el principio de Pareto se manifiesta en cómo las ideas rompedoras surgen de un subconjunto sorprendentemente pequeño de intentos. Empresas como Apple y Google han descubierto que aproximadamente el 20% de sus productos generan el 80% de sus ingresos, mientras que en la investigación científica, una pequeña fracción de artículos obtiene la mayoría de las citas. Este patrón aparece en todas las industrias creativas, desde las canciones de éxito de los catálogos musicales hasta las películas de éxito de las carteras de los estudios.

Ondas sociales: el efecto red

El principio de Pareto se manifiesta en cómo se propaga la información a través de las redes sociales. Un grupo selecto de personas influyentes, que representan quizás el 20% de los usuarios, a menudo impulsan el 80% de la participación en las plataformas sociales. Este mismo patrón aparece en la viralidad de los contenidos, donde un pequeño porcentaje de publicaciones acapara la mayoría de comparticiones e interacciones.

Conclusión

La distribución de Pareto pone de relieve cómo las herramientas estadísticas pueden revelar patrones significativos de concentración en los datos. Para ampliar tu comprensión de estos conceptos, te ofrecemos valiosas oportunidades de aprendizaje. Nuestro curso Fundamentos de la Probabilidad en R introduce los principios básicos, mientras que Introducción al Análisis de Carteras en R demuestra cómo se aplican estas ideas a contextos financieros. Además, nuestro tutorial Probabilidad y Estadística en el Póquer con Python ofrece una forma única de explorar los conceptos de probabilidad en acción, haciendo que el aprendizaje sea atractivo y práctico. Estos recursos proporcionan una base sólida para aplicar los conocimientos estadísticos en una serie de situaciones prácticas.