Lei de Potência: Um padrão por trás dos eventos extremos

Já pensou por que alguns sites recebem a maior parte do tráfego da internet? Ou por que uma pequena parte das pessoas controla a maior parte da riqueza do mundo? A resposta está num fenômeno estatístico bem interessante chamado lei de potência. 

As leis de potência controlam muitos sistemas naturais e artificiais. Essas distribuições são especiais porque não mudam com a escala e têm caudas pesadas. Essas características fazem com que sejam perfeitos para modelar dados onde acontecem muitos eventos pequenos, mas eventos grandes e importantes, mesmo que sejam raros, não podem ser ignorados.

Esse tutorial vai te dar uma visão geral das leis de potência, incluindo a teoria, a matemática, os usos e como estimá-las. Vamos ver como eles são invariantes em escala e por que aparecem em áreas diferentes, como geofísica, finanças, biologia e internet.

Propriedades das distribuições da lei de potência

Vamos começar com o que torna as leis de potência especiais — e como elas são diferentes das distribuições que você já deve ter usado até agora. 

Características das leis de potência. Fonte: IA para guardanapos

Invariante em escala e auto-similaridade

Simplificando, a invariância de escala quer dizer que, se você aumentar ou diminuir o zoom, o padrão na distribuição continua o mesmo. 

Em termos estatísticos, uma distribuição de lei de potência tem a mesma forma funcional, não importa em que escala você olhe para ela. Se uma variável segue uma lei de potência, multiplicá-la por uma constante não muda a forma como ela é distribuída; só muda a escala.

Em termos matemáticos, isso quer dizer que:

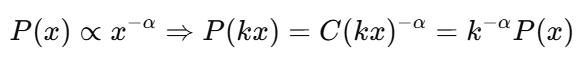
Isso é bem diferente de outras distribuições comuns, como a distribuição normal, onde aforma é definida com base em alguns parâmetros importantes, como a média e o desvio padrão.

Essa propriedade também é parecida com a auto-similaridade, que é uma característica importante dos fractais. Fractais são estruturas que parecem iguais, não importa o quanto você amplie a imagem. Por exemplo, se você ampliar qualquer parte de um floco de neve, folha de samambaia ou galho de árvore, verá uma versão menor do objeto inteiro. 

A costa parece igual a 10 metros de distância e a 10 quilômetros de distância. 

As leis de potência são ótimas pra mostrar essa estrutura que se repete. É por isso que eles são úteis quando a gente está olhando para sistemas onde o tamanho, a frequência ou a intensidade mudam bastante, mas sempre seguem o mesmo padrão.

Cauda pesada e falta de escala característica

A maioria das distribuições clássicas (como gaussiana ou exponencial) diminuem rapidamente nas extremidades. Não é assim com as leis de potência. Eles têmcaudas pesadas d , o que significa que a probabilidade de eventos extremos é maior.

Na vida real, grandes terremotos, tweets virais e bilionários são exemplos de coisas raras que ainda podem acontecer. Na verdade, para alguns valores de alfa, momentos como média ou variância podem nem existir, e é por isso que dizemos que as distribuições de lei de potência não têm escala. 

Universalidade e incompletude estatística

Uma coisa incrível sobre as leis de potência é que elas são universais; elas podem ser encontradas em sistemas que parecem não ter nenhuma relação entre si. Alguns exemplos disso são: magnitude de terremotos, picos na atividade neural, tamanho das empresas e frequência de palavras. 

O outro lado da moeda é que eles também são estatisticamente incompletos. Isso quer dizer que, mesmo que a gente consiga modelar como a cauda se comporta, é difícil estimar um conjunto completo de estatísticas resumidas, principalmente a partir de amostras pequenas de dados. 

Fundamentos matemáticos das leis de potência

Vamos mergulhar mais fundo na matemática que torna as leis de potência tão poderosas e complicadas.

Forma funcional e propriedades de escala

A forma padrão de uma lei de potência é:

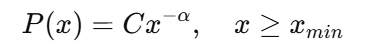
Onde:

• alfa é o exponente de escala
• C é a constante normalizadora
• x_min​ é olimite do o acima do qual a lei de potência se mantém

À medida que o alfa aumenta, a cauda fica mais fina. Um alfa pequeno quer dizer que os eventos são mais extremos. Esse expoente de escala controla tudo, desde a desigualdade até o tamanho dos ecossistemas.

Distribuições de probabilidade da lei de potência e gráficos logarítmicos

O primeiro passo é usar um gráfico log-log para detectar uma lei de potência em conjuntos de dados reais.

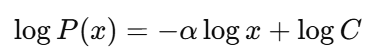
Se os dados realmente seguem uma lei de potência, isso vai te dar uma linha reta com uma inclinação de −α. Mas cuidado, porque muitas distribuições parecem lineares em um gráfico logarítmico. 

Relações com outras distribuições

Existem várias distribuições estatísticas importantes que são parecidas com as leis de potência.

• As distribuições de Pareto, que são muito usadas em economia, mostram como a riqueza e a renda são distribuídas, onde poucas pessoas têm a maior parte dos recursos. Esse é um dos primeiros e clássicos exemplos de uma lei de potência em ação.
• A lei de Zipf explica como a frequência das palavras na linguagem natural segue um padrão de lei de potência. Por exemplo, a segunda palavra mais comum aparece mais ou menos metade das vezes que a palavra mais comum, a terceira aparece mais ou menos um terço das vezes, e assim por diante.
• A distribuição zeta é uma versão discreta da lei de potência que é frequentemente usada para modelar coisas que acontecem com frequência, como acessos a sites ou vendas de livros.

Às vezes, os dados do mundo real não seguem uma lei de potência “pura” para sempre. Nessas situações, a gente vê cortes exponenciais (onde valores muito grandes ficam menos prováveis), leis de potência curvas ou caudas log-normais. Esses são melhores pra modelar sistemas com limites físicos ou práticos. Esses híbridos sabem que a invariância de escala pode funcionar para parte da faixa, mas que, eventualmente, deixará de funcionar.

Manifestações empíricas em várias áreas

As leis de potência não são só ideias matemáticas; elas aparecem no mundo real e nos ajudam a entender sistemas que, à primeira vista, parecem aleatórios ou caóticos.

Sistemas naturais e geofísicos

As leis de potência ajudam a entender eventos extremos na natureza. Por exemplo, a lei de Gutenberg-Richter diz que a magnitude dos terremotos segue uma distribuição de lei de potência. Isso quer dizer que pequenos tremores rolam bastante, mas conforme a intensidade do terremoto aumenta, o número de tremores cai rapidinho. É por isso que um terremoto de magnitude 2,0 pode acontecer todos os dias, mas um terremoto de magnitude 7,0 pode não acontecer por anos. Os dois fazem parte da mesma história estatística. 

Da mesma forma, redes fluviais, linhas costeiras e até mesmo raios apresentam padrões fractais auto-similares que seguem uma escala de potência nos tamanhos de seus segmentos.

As leis de potência também se aplicam ao universo. Na astrofísica, a gente vê que o tamanho das estrelas, a distribuição dos buracos negros e até mesmo os aglomerados de galáxias têm caudas pesadas. Tem um monte de estrelas pequenas, mas só algumas grandes se destacam na galáxia. Pode parecer que essa diferença é aleatória, mas quando a gente entende a lei de potência que está por trás disso, dá pra ver que ela segue certas regras estatísticas.

Sistemas socioeconômicos e biológicos

Quando a gente pensa em desigualdade e escala nas sociedades humanas, as leis de potência são super úteis. Já falamos sobre a distribuição de Pareto na seção anterior, que não é só uma teoria sobre economia; dá pra ver isso em registros fiscais, lucros corporativos e padrões de doações. 

Os 1% mais ricos seguem a lei de Pareto, não as médias gaussianas. Essas distribuições não se encaixam em uma curva normal; em vez disso, elas se estendem muito para a direita, mostrando alguns valores extremos (como bilionários) que distorcem a média.

As leis de potência também mostram padrões escondidos na biologia. Por exemplo, a lei de Kleiber diz que a taxa metabólica de um animal aumenta à medida que sua massa corporal aumenta à potência de 3/4, e não em linha reta. Isso ajuda a entender por que um elefante não come mil vezes mais do que um coelho, mesmo pesando mil vezes mais. 

As leis de potência também se aplicam à população das cidades, às taxas de crescimento das empresas, ao comportamento eleitoral e até mesmo às mortes em conflitos, onde poucas coisas ou eventos importantes têm um efeito desproporcional.

Tecnologia e negócios

As leis de potência são o que mantêm o mundo digital funcionando e prosperando. Pensa em como funciona o tráfego na internet: só alguns sites (como Google, Facebook e YouTube) recebem a maioria das visitas, enquanto milhões de outras páginas passam quase despercebidas. Esse é um comportamento típico da cauda longa e é super importante em áreas como SEO, mecanismos de recomendação e marketing digital.

Na IA, o tamanho e o desempenho dos modelos geralmente seguem a mesma direção. Tem alguns modelos grandes, tipo o GPT-4, que são os melhores no assunto, mas centenas de modelos menores não conseguem acompanhar. Essa concentração é em parte por causa dos ciclos de feedback: modelos melhores atraem mais usuários, dados e dinheiro, o que os torna ainda mais poderosos. 

Estimativa estatística e validação

Então, parece que seu conjunto de dados segue uma lei de potência. O histograma pode ter uma cauda longa ou o gráfico log-log pode mostrar uma linha quase reta. É um bom começo, mas só olhar não é suficiente, porque é fácil se enganar com as leis de potência. É por isso que precisamos de boas ferramentas estatísticas para descobrir os parâmetros e verificar se estão certos.

Métodos de estimativa de parâmetros

O expoente de escala, que geralmente é escrito como 𝛼, é a primeira coisa que você precisa para modelar corretamente uma distribuição de lei de potência. 

A Estimativa de Máxima Verossimilhança (MLE) é uma das formas mais comuns de obter uma estimativa de 𝛼. É uma maneira de encontrar os valores dos parâmetros que tornam os dados observados mais prováveis em todas as estatísticas.

Para dados contínuos com um valor mínimo conhecido 𝑥min, é assim que funciona:

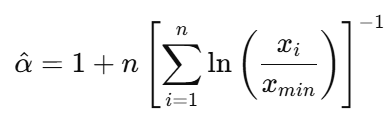
• 𝑥𝑖 são os valores que você viu, e todos eles são maiores ou iguais a 𝑥𝑚𝑖𝑛.
• 𝑛 é o número de observações.

Mas aqui está a parte difícil: escolher o 𝑥 min certo é muito importante. Se estiver muito baixo, seu modelo tem dados que não seguem realmente a lei de potência. E se estiver muito alto, você vai acabar gastando muitos dados. Além disso, quando as amostras são pequenas, as estimativas MLE podem não ser muito confiáveis.

Teste de adequação

Depois de estimar o expoente, a próxima pergunta é: ele se encaixa bem? Você não pode simplesmente dizer: “Parece uma lei de potência”. Você precisa de evidências estatísticas de que a lei de potência explica melhor seus dados do que outras distribuições possíveis. É aqui que entra em cena o testede Kolmogorov-Smirnov (KS). Esse teste encontra a maior diferença entre a função de distribuição cumulativa (CDF) dos dados observados e o modelo teórico da lei de potência. 

Quanto mais perto esse número estiver de zero, melhor o seu modelo se encaixa nos dados. O teste KS não usa agrupamento ou histogramas como muitos outros testes. Em vez disso, ele trabalha diretamente com os dados brutos, o que o torna muito útil para distribuições de cauda pesada.Mas, às vezes, uma lei de potência não é a única explicação plausível. Uma distribuição log-normal ou exponencial também pode ser capaz de modelar seus dados. É aí queos testes de razão de verossimilhanç são úteis. A ideia é simples: usa o MLE pra ajustar os dois modelos aos mesmos dados, encontra as probabilidades e compara. Você tem suporte estatístico para o modelo da lei de potência se a probabilidade dele for bem maior. 

A estrutura de Clauset-Shalizi-Newman (2009) é uma das muitas ferramentas que juntam MLE, testes KS e testes de razão de verossimilhança numa maneira forte de ver o comportamento da lei de potência.

Mecanismos teóricos e modelos gerativos

Agora que já sabemos onde as leis de potência aparecem no mundo real e como encontrá-las estatisticamente, a próxima pergunta é: por que essas distribuições aparecem? Vamos ver como as leis de potência podem surgir da dinâmica dos sistemas.

Anexação preferencial e processos de Yule

O modelo de Barabási-Albert (1999) trouxe a ideia de ligação preferencial, que geralmente é resumida como o fenômeno “os ricos ficam mais ricos”. É uma das formas mais conhecidas e fáceis de entender como funcionam as leis de potência. 

Pense em criar uma rede, tipo a internet ou uma rede social. Quando um novo usuário entra, é mais provável que ele se conecte a nós populares, como Facebook ou Google, porque esses nós já são bem conhecidos. 

Com o tempo, isso cria um ciclo vicioso: os nós populares ficam ainda mais conectados, enquanto os mais novos ou menos conectados continuam pequenos. Isso cria uma rede sem escala, onde os graus dos nós seguem uma lei de potência.

Da mesma forma, os processos de Yule modelam o crescimento dos gêneros biológicos, o que é uma extensão dessa ideia. Nesse modelo, as espécies que já têm mais membros têm mais chances de dar origem a novas espécies. Isso faz com que a distribuição fique meio torta, com só alguns gêneros dominando.

Modelos de crescimento aleatório, lei de Gibrat e processos de Markov

Os processos de crescimento aleatório são outra forma de as leis de potência aparecerem. A ideia principal é que as coisas ficam maiores com o tempo, multiplicando quantidades aleatórias em vez de somá-las. 

A lei de Gibrat diz que a taxa de crescimento não depende do tamanho. A maioria das coisas permanece pequena, mas algumas crescem muito rápido e ficam bem grandes, formando a cauda pesada de uma lei de potência. 

Os processos de Markov, especialmente aqueles que envolvem ruído multiplicativo, também podem convergir para distribuições estacionárias semelhantes à lei de potência — especialmente sob limites refletivos.

Também tem um lado de probabilidade nisso. Os processos de Markov também podem mostrar um comportamento de lei de potência em algumas situações. Esses processos modelam sistemas em que o próximo estado depende apenas do atual, e não do passado. As pessoas têm usado isso pra modelar coisas como a forma como as pessoas se movimentam numa população e como funcionam as filas.

Esses modelos não são só ideias interessantes. Elas nos ajudam a entender como sistemas complexos mudam com o tempo, por que a desigualdade continua a mesma e como os efeitos de rede afetam tudo, desde a biologia até o blockchain. Não só podemos usar leis de potência para descrever o mundo, como também podemos usá-las para explicá-lo.

Implicações, limitações e aplicações

Entender a dinâmica das leis de potência é super importante e pode ter um grande efeito nas suas previsões e escolhas, seja na criação de um modelo de risco financeiro, na gestão de uma infraestrutura de internet ou no estudo do comportamento social. 

Considerações práticas

Os modelos de lei de potência são úteis para sistemas onde acontecem eventos raros, mas importantes. Por exemplo, no mundo das finanças, os preços podem mudar normalmente na maioria dos dias, mas os “cisnes negros” — aquelas quedas ou altas raras — podem ter o maior impacto. 

Os modelos de lei de potência conseguem captar melhor esse risco de cauda do que os modelos tradicionais, que muitas vezes subestimam a probabilidade de esses eventos acontecerem. Para gerenciamento de riscos, seguros, segurança cibernética e planejamento para desastres, isso é muito importante.

Tem também a vantagem de entender o crescimento não linear e os efeitos compostos. As leis de potência ajudam a entender por que algumas pessoas, empresas ou nós numa rede podem se tornar os mais poderosos com o tempo e por que essas situações de “o vencedor leva tudo” não são só raras, mas normais nesse tipo de sistema.

Mas tem algumas desvantagens nos modelos de lei de potência. Um problema é que eles desafiam a intuição, pois nem sempre têm médias ou variações claras, o que dificulta a determinação de métricas comuns, como “valor esperado” ou “desvio padrão”.

Esses modelos geralmente só funcionam na cauda da distribuição, então podem não se encaixar bem ou nem se encaixar nos dados em geral. Isso pode ser um problema se você não prestar atenção em onde o comportamento da lei de potência realmente começa.

Limitações e críticas

Nem todos os conjuntos de dados com caudas longas seguem uma lei de potência real. Poucas distribuições, como a log-normal ou a exponencial estendida, podem parecer um comportamento de lei de potência em um intervalo pequeno, especialmente em um gráfico log-log. Isso muitas vezes leva a falsos positivos, em que consideramos que se trata de uma lei de potência só porque o gráfico “parece linear”.A generalização excessiva é outro problema. Muita gente acha que as leis de potência explicam tudo sobre um sistema, mas elas podem explicar só uma parte, geralmente a parte mais extrema. Por exemplo, os 1% mais ricos podem ter uma lei de potência para a distribuição de renda, mas o resto da galera pode ter uma bem diferente.

A lei dos rendimentos decrescentes é outro problema que os sistemas do mundo real enfrentam. As leis de potência dizem que resultados extremos são possíveis, mas em algumas áreas, tipo limites físicos ou ambientes regulatórios, tem limites além dos quais o modelo não funciona mais. Se você acha que o comportamento da cauda vai continuar pra sempre, pode acabar achando que os riscos ou recompensas são maiores do que realmente são, principalmente em sistemas com limites.

Conclusão

As leis de potência ajudam a entender sistemas onde alguns eventos ou coisas extremos têm um efeito grande, tipo terremotos, tráfego na internet ou como a renda é distribuída. Neste tutorial, a gente aprendeu o que torna as leis de potência diferentes, suas propriedades matemáticas e marcas empíricas, como encontrá-las e verificá-las, e onde elas podem ser encontradas no mundo real.

A análise da lei de potência vai ter usos bem legais no futuro em áreas como IA, economia, ciência de redes e gestão de riscos. Podemos usá-los para entender melhor um mundo complicado e não linear, se tivermos as ferramentas e o conhecimento certos.

À medida que você mergulha mais fundo nos dados do mundo real, sempre se pergunte: o que é raro é realmente raro ou é só que está bem distribuído?

Se você quiser saber mais sobre alguns dos conceitos, dá uma olhada nesses recursos:

• Folha de dicas sobre regras de probabilidade
• Guia de Notação Big O e Complexidade Temporal
• Modelos lineares generalizados em Python