Potenzgesetz: Ein Muster hinter extremen Ereignissen

Hast du dich schon mal gefragt, warum ein paar Websites den Großteil des Internetverkehrs bekommen? Oder warum hat nur ein kleiner Teil der Leute die meiste Kohle auf der Welt? Die Antwort liegt in einem coolen statistischen Phänomen, das als Potenzgesetz bekannt ist. 

Potenzgesetze bestimmen viele natürliche und von Menschen geschaffene Systeme. Diese Verteilungen sind besonders, weil sie sich nicht mit der Größe ändern und dicke Enden haben. Diese Eigenschaften machen sie super für die Modellierung von Daten, bei denen viele kleine Ereignisse passieren, aber große, wichtige Ereignisse, auch wenn sie selten sind, nicht ignoriert werden dürfen.

Dieses Tutorial gibt dir einen umfassenden Überblick über Potenzgesetze, einschließlich ihrer Theorie, Mathematik, Anwendungen und wie man sie schätzt. Wir schauen uns an, wie sie skalierungsinvariant sind und warum sie in so unterschiedlichen Bereichen wie Geophysik, Finanzwesen, Biologie und im Internet auftauchen.

Eigenschaften von Potenzgesetzverteilungen

Fangen wir mal damit an, was Potenzgesetze so besonders macht – und wie sie sich von den Verteilungen unterscheiden, die du vielleicht bisher benutzt hast. 

Eigenschaften von Potenzgesetzen. Quelle: Napkin AI

Skalierungsinvarianz und Selbstähnlichkeit

Einfach gesagt bedeutet Skaleninvarianz, dass das Muster in der Verteilung gleich bleibt, egal ob du rein- oder rauszoomst. 

Statistisch gesehen hat eine Potenzgesetzverteilung immer die gleiche Form, egal in welchem Maßstab man sie betrachtet. Wenn eine Variable einem Potenzgesetz folgt, ändert das Multiplizieren mit einer Konstanten nichts an ihrer Verteilung, sondern nur an der Skala.

Mathematisch bedeutet das:

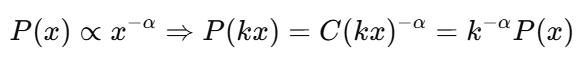
Das ist ganz anders als bei anderen gängigen Verteilungen, wie der Normalverteilung, wo dieForm anhand von bestimmten Schlüsselparametern wie dem Mittelwert und der Standardabweichung festgelegt wird.

Diese Eigenschaft ähnelt auch der Selbstähnlichkeit, die ein wichtiges Merkmal von Fraktalen ist. Fraktale sind Strukturen, die immer gleich aussehen, egal wie stark man sie vergrößert. Wenn du zum Beispiel einen Teil einer Schneeflocke, eines Farnblatts oder eines Astes vergrößerst, siehst du eine kleinere Version des Ganzen. 

Eine Küste sieht aus 10 Metern Entfernung genauso aus wie aus 10 Kilometern Entfernung. 

Potenzgesetze zeigen diese sich wiederholende Struktur sehr gut. Deshalb sind sie nützlich, wenn man Systeme betrachtet, bei denen Größe, Häufigkeit oder Intensität stark schwanken, aber immer dem gleichen Muster folgen.

Schwere Schwänze und fehlende charakteristische Skala

Die meisten klassischen Verteilungen (wie Gauß oder Exponential) fallen in den Randbereichen schnell ab. Bei Potenzgesetzen ist das anders. Sie haben„ “ (dicke Schwänze), was bedeutet, dass die Wahrscheinlichkeit von Extremereignissen höher ist.

Im echten Leben sind große Erdbeben, virale Tweets und Milliardäre Beispiele für seltene Ereignisse, die trotzdem passieren können. Tatsächlich können Momente wie Mittelwert oder Varianz für einige Werte von Alpha sogar ganz fehlen, und deshalb sagen wir, dass Potenzgesetzverteilungen keine Skala haben. 

Allgemeingültigkeit und statistische Unvollständigkeit

Das Coole an Potenzgesetzen ist, dass sie überall gelten; man findet sie in Systemen, die auf den ersten Blick nichts miteinander zu tun haben. Einige Beispiele dafür sind: Stärke von Erdbeben, Spitzenwerte bei der neuronalen Aktivität, Größe von Unternehmen und Häufigkeit von Wörtern. 

Die Kehrseite ist, dass sie auch statistisch unvollständig sind. Das heißt, auch wenn wir das Verhalten des Schwanzes modellieren können, ist es schwierig, einen vollständigen Satz von zusammenfassenden Statistiken zu schätzen, vor allem bei kleinen Datenmengen. 

Mathematische Grundlagen von Potenzgesetzen

Schauen wir uns mal genauer an, warum Potenzgesetze so mächtig und knifflig sind.

Funktionsform und Skalierungseigenschaften

Die Standardform eines Potenzgesetzes lautet:

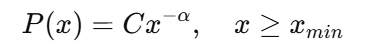
Wo:

• alpha ist der Skalierungsexponent
• C ist die Normalisierungskonstante
• x_min​ ist derSchwellenwert „ “, ab dem das Potenzgesetz gilt.

Mit zunehmendem Alpha wird der Schwanz dünner. Ein kleiner Alpha-Wert bedeutet, dass Ereignisse extremer sind. Dieser Skalierungsexponent bestimmt alles, von Ungleichheit bis hin zur Größe von Ökosystemen.

Potenzgesetz-Wahrscheinlichkeitsverteilungen und logarithmische Diagramme

Der erste Schritt ist die Verwendung eines Log-Log-Diagramm , um ein Potenzgesetz in echten Datensätzen zu erkennen.

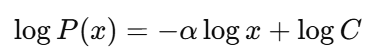
Wenn die Daten wirklich einem Potenzgesetz folgen, bekommst du eine gerade Linie mit einer Steigung von −α. Aber pass auf, viele Verteilungen sehen auf einem Log-Log-Diagramm linear aus. 

Verwandte Distributionen

Es gibt ein paar wichtige statistische Verteilungen, die so ähnlich wie Potenzgesetze sind.

• Die in der Wirtschaft häufig verwendeten Pareto-Verteilungen zeigen die Verteilung von Vermögen und Einkommen, bei der eine kleine Anzahl von Menschen den Großteil der Ressourcen besitzt. Das ist ein frühes und klassisches Beispiel für ein Potenzgesetz in Aktion.
• Das Zipfsche Gesetz erklärt, wie die Häufigkeit von Wörtern in natürlicher Sprache einem Potenzgesetz folgt. Zum Beispiel kommt das zweithäufigste Wort ungefähr halb so oft vor wie das häufigste Wort, das dritthäufigste ungefähr ein Drittel so oft und so weiter.
• Die Zeta-Verteilung ist eine diskrete Version des Potenzgesetzes, die oft verwendet wird, um Dinge zu modellieren, die häufig vorkommen, wie Website-Zugriffe oder Buchverkäufe.

Manchmal folgen die Daten aus der echten Welt nicht immer einem „reinen“ Potenzgesetz. In solchen Situationen sehen wir exponentielle Cutoffs (wo sehr große Werte immer unwahrscheinlicher werden), gekrümmte Potenzgesetze oder logarithmisch-normale Verteilungen. Diese eignen sich besser für die Modellierung von Systemen mit physikalischen oder praktischen Einschränkungen. Diese Hybride wissen, dass Skaleninvarianz vielleicht für einen Teil des Bereichs funktioniert, aber irgendwann nicht mehr.

Empirische Erscheinungsformen in verschiedenen Fachbereichen

Potenzgesetze sind nicht nur so eine Idee aus der Matheklasse, sondern tauchen auch in der echten Welt auf und helfen uns, Systeme zu verstehen, die auf den ersten Blick zufällig oder chaotisch wirken.

Natürliche und geophysikalische Systeme

Potenzgesetze helfen uns, extreme Ereignisse in der Natur zu verstehen. Zum Beispiel besagt das Gutenberg-Richter-Gesetz, dass die Stärke von Erdbeben einer Potenzgesetzverteilung folgt. Das heißt, dass es oft kleine Beben gibt, aber je stärker das Beben wird, desto weniger Beben gibt's. Deshalb kann es jeden Tag ein Beben der Stärke 2,0 geben, aber vielleicht jahrelang kein Beben der Stärke 7,0. Beides ist Teil derselben statistischen Geschichte. 

Genauso zeigen Flussnetze, Küstenlinien und sogar Blitze selbstähnliche, fraktale Muster, die in der Größe ihrer Teile einem Potenzgesetz folgen.

Potenzgesetze gelten auch für das Universum. In der Astrophysik sehen wir, dass die Größe von Sternen, die Verteilung von Schwarzen Löchern und sogar die Galaxienhaufen alle schwere Schwänze haben. Es gibt Milliarden kleiner Sterne, aber nur ein paar ganz große fallen in der Galaxie auf. Es mag so aussehen, als ob diese Ungleichmäßigkeit zufällig ist, aber wenn wir das Potenzgesetz verstehen, das dahintersteckt, sehen wir, dass sie bestimmten statistischen Regeln folgt.

Sozioökonomische und biologische Systeme

Wenn man Ungleichheit und Größe in menschlichen Gesellschaften betrachtet, sind Potenzgesetze besonders hilfreich. Wir haben die Pareto-Verteilung schon im letzten Abschnitt besprochen. Das ist nicht nur so eine Wirtschaftstheorie, sondern man sieht sie auch in Steuerunterlagen, Unternehmensgewinnen und Spendenmustern. 

Die obersten 1 % der Leute mit viel Geld folgen dem Pareto-Prinzip, nicht dem Gaußschen Durchschnitt. Diese Verteilungen passen nicht in eine ordentliche Glockenkurve, sondern erstrecken sich weit nach rechts und zeigen ein paar extreme Werte (wie Milliardäre), die den Durchschnitt nach oben ziehen.

Potenzgesetze zeigen auch versteckte Muster in der Biologie. Kleibers Gesetz besagt zum Beispiel, dass der Stoffwechsel eines Tieres nicht linear mit seiner Körpermasse steigt, sondern mit der 3/4-Potenz. Das hilft uns zu verstehen, warum ein Elefant nicht tausendmal mehr frisst als ein Kaninchen, obwohl er tausendmal mehr wiegt. 

Potenzgesetze gelten auch für die Einwohnerzahlen von Städten, das Wachstum von Unternehmen, das Wahlverhalten und sogar für Todesfälle in Konflikten, wo ein paar große Dinge oder Ereignisse einen überproportionalen Einfluss haben.

Technologie und Wirtschaft

Potenzen sind das, was die digitale Welt am Laufen hält und wachsen lässt. Überleg mal, wie der Datenverkehr im Internet läuft: Nur ein paar Websites (wie Google, Facebook und YouTube) kriegen die meisten Besuche, während Millionen anderer Seiten fast gar nicht bemerkt werden. Das ist typisch für das Long-Tail-Verhalten und besonders wichtig in Bereichen wie SEO, Empfehlungsmaschinen und digitalem Marketing.

Bei KI entwickeln sich die Größe und die Leistung von Modellen meistens in die gleiche Richtung. Es gibt ein paar große Modelle wie GPT-4, die in diesem Bereich echt top sind, aber Hunderte von kleineren Modellen können da nicht mithalten. Diese Konzentration kommt zum Teil durch Rückkopplungsschleifen: Bessere Modelle kriegen mehr Nutzer, Daten und Geld, was sie noch besser macht. 

Statistische Schätzung und Validierung

Es sieht also so aus, als würde dein Datensatz einem Potenzgesetz folgen. Das Histogramm könnte einen langen Schwanz haben oder die logarithmische Darstellung könnte eine fast gerade Linie zeigen. Das ist schon mal ein guter Anfang, aber nur draufzuschauen reicht nicht, weil man sich leicht von Potenzgesetzen täuschen lassen kann. Deshalb brauchen wir gute Statistik-Tools, um die Parameter zu ermitteln und die Passgenauigkeit zu überprüfen.

Methoden zur Parameterschätzung

Der Skalierungsexponent, der normalerweise mit 𝛼 geschrieben wird, ist das Erste, was du brauchst, um eine Potenzgesetzverteilung richtig zu modellieren. 

Die Maximum-Likelihood-Schätzung (MLE) ist eine der gängigsten Methoden, um eine Schätzung von 𝛼 zu erhalten. Das ist eine Methode, um die Parameterwerte zu finden, die die beobachteten Daten in der Statistik am wahrscheinlichsten machen.

Bei kontinuierlichen Daten mit einem bekannten Minimalwert 𝑥min geht's so:

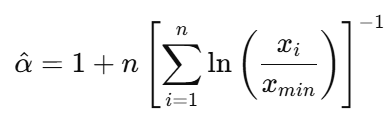
• 𝑥𝑖 sind die Werte, die du gesehen hast, und sie sind alle größer oder gleich 𝑥𝑚𝑖𝑛.
• 𝑛 ist die Anzahl der Beobachtungen.

Aber hier kommt der schwierige Teil: Die Wahl des richtigen 𝑥 min ist echt wichtig. Wenn der Wert zu niedrig ist, hat dein Modell Daten, die nicht wirklich dem Potenzgesetz folgen. Und wenn er zu hoch ist, verschwendest du am Ende zu viel Datenvolumen. Außerdem können MLE-Schätzungen bei kleinen Stichproben unzuverlässig sein.

Passungsprüfung

Nachdem du den Exponenten geschätzt hast, kommt die nächste Frage: Wie gut passt er? Man kann nicht einfach sagen: „Das sieht irgendwie nach einem Potenzgesetz aus.“ Du brauchst statistische Beweise dafür, dass das Potenzgesetz deine Daten besser erklärt als andere mögliche Verteilungen. Hier kommt der Kolmogorov-Smirnov-Test (KS-Test) ins Spiel:. Dieser Test findet die größte Lücke zwischen der kumulativen Verteilungsfunktion (CDF) deiner beobachteten Daten und dem theoretischen Potenzgesetzmodell. 

Je näher dieser Wert an Null ist, desto besser passt dein Modell zu den Daten. Der KS-Test verwendet keine Klassifizierung oder Histogramme wie viele andere Tests. Stattdessen arbeitet es direkt mit den Rohdaten, was es super für Verteilungen mit schweren Enden macht.Aber manchmal ist ein Potenzgesetz nicht die einzige plausible Erklärung. Eine logarithmisch-normale oder exponentielle Verteilung könnte auch gut zu deinen Daten passen. In solchen Fällen sindLikelihood-Ratio-Tests nach nützlich. Die Idee ist ganz einfach: Man passt mit MLE beide Modelle an die gleichen Daten an, ermittelt die Wahrscheinlichkeiten und vergleicht sie dann miteinander. Du hast statistische Unterstützung für das Potenzgesetzmodell, wenn dessen Wahrscheinlichkeit deutlich höher ist. 

Das Clauset-Shalizi-Newman-Modell (2009) ist eines von vielen Tools, die MLE, KS-Tests und Likelihood-Ratio-Tests kombinieren, um das Verhalten von Potenzgesetzen besser zu verstehen.

Theoretische Mechanismen und generative Modelle

Jetzt, wo wir wissen, wo man Potenzgesetze in der echten Welt findet und wie man sie statistisch herausfindet, kommt die nächste Frage: Warum gibt es diese Verteilungen überhaupt? Schauen wir mal, wie sich Potenzgesetze aus der Systemdynamik ergeben können.

Bevorzugte Bindung und Yule-Prozesse

Das Barabási-Albert-Modell (1999) hat die bevorzugte Anbindung eingeführt, die oft als „die Reichen werden reicher”-Phänomen zusammengefasst wird. Das ist eine der bekanntesten und einfachsten Arten, wie Potenzgesetze funktionieren. 

Überleg dir, ein Netzwerk aufzubauen, wie das Internet oder eine Social-Media-Seite. Wenn jemand neu dabei ist, verbindet er sich eher mit bekannten Knoten wie Facebook oder Google, weil die schon bekannt sind. 

Mit der Zeit entsteht so eine Art Kreislauf: Beliebte Knotenpunkte kriegen noch mehr Verbindungen, während neuere oder weniger vernetzte Knotenpunkte klein bleiben. Dadurch entsteht ein skalierungsfreies Netzwerk, in dem die Grade der Knoten einem Potenzgesetz folgen.

Ähnlich modelliert das Yule-Prozessmodell das Wachstum biologischer Gattungen und ist eine Erweiterung dieser Idee. In diesem Modell ist es wahrscheinlicher, dass Arten, die schon mehr Mitglieder haben, neue Arten hervorbringen. Das führt zu einer schrägen Verteilung, wo nur ein paar Gattungen das Sagen haben.

Zufällige Wachstumsmodelle, Gibrats Gesetz und Markov-Prozesse

Zufällige Wachstumsprozesse sind noch eine andere Art, wie sich Potenzgesetze zeigen können. Die Hauptidee ist, dass Dinge mit der Zeit größer werden, indem man zufällige Mengen multipliziert, anstatt sie zu addieren. 

Das Gesetz von Gibrat besagt, dass die Wachstumsrate unabhängig von der Größe ist. Die meisten Sachen bleiben klein, aber ein paar wachsen echt schnell und werden richtig groß, was zu dem schweren Schwanz einer Potenzgesetzkurve führt. 

Markov-Prozesse, vor allem solche mit multiplikativem Rauschen, können auch zu stationären Verteilungen konvergieren, die wie Potenzgesetze aussehen – besonders bei reflektierenden Grenzen.

Das hat auch eine Wahrscheinlichkeitsseite. Markov-Prozesse können in manchen Situationen auch ein Potenzgesetz-Verhalten zeigen. Diese Prozesse zeigen Systeme, bei denen der nächste Zustand nur vom aktuellen Zustand abhängt, nicht von dem, was vorher war. Das hat man schon benutzt, um Sachen zu modellieren, wie zum Beispiel, wie sich Leute in einer Population bewegen und wie Warteschlangen funktionieren.

Diese Modelle sind nicht nur coole Ideen. Sie helfen uns zu verstehen, wie komplexe Systeme sich mit der Zeit verändern, warum Ungleichheit bestehen bleibt und wie Netzwerkeffekte alles beeinflussen, von der Biologie bis zur Blockchain. Mit Potenzgesetzen können wir die Welt nicht nur beschreiben, sondern auch erklären.

Auswirkungen, Einschränkungen und Anwendungen

Die Dynamik von Potenzgesetzen zu verstehen ist mega wichtig und kann deine Vorhersagen und Entscheidungen stark beeinflussen, egal ob du ein Finanzrisikomodell erstellst, eine Internetinfrastruktur betreibst oder soziales Verhalten studierst. 

Praktische Überlegungen

Potenzgesetz-Modelle sind super für Systeme, in denen seltene, aber wichtige Ereignisse passieren. In der Finanzwelt zum Beispiel können sich die Preise an den meisten Tagen ganz normal entwickeln, aber die „schwarzen Schwäne“ – also die seltenen Crashs oder Booms – können die größten Auswirkungen haben. 

Power-Law-Modelle können dieses Tail-Risiko besser erfassen als herkömmliche Modelle, die die Wahrscheinlichkeit solcher Ereignisse oft unterschätzen. Für Risikomanagement, Versicherungen, Cybersicherheit und Notfallplanung ist das echt wichtig.

Außerdem ist es cool, nichtlineares Wachstum und Zinseszinseffekte zu verstehen. Potenzgesetze helfen zu erklären, warum manche Leute, Firmen oder Knotenpunkte in einem Netzwerk mit der Zeit die mächtigsten werden und warum diese „Der Gewinner bekommt alles“-Situationen in solchen Systemen nicht nur ungewöhnlich, sondern ganz normal sind.

Aber bei Potenzgesetz-Modellen gibt's auch ein paar Nachteile. Ein Problem ist, dass sie nicht intuitiv sind – sie haben nicht immer klare Durchschnittswerte oder Abweichungen, was es schwierig macht, gängige Kennzahlen wie den „erwarteten Wert“ oder die „Standardabweichung“ zu ermitteln.

Diese Modelle funktionieren normalerweise nur am Ende der Verteilung, sodass sie möglicherweise nicht gut oder gar nicht zum Großteil der Daten passen. Das kann ein Problem sein, wenn du nicht genau darauf achtest, wo das Potenzgesetz-Verhalten tatsächlich einsetzt.

Einschränkungen und Kritik

Nicht alle Datensätze mit langen Schwänzen folgen einem echten Potenzgesetz. Nur wenige Verteilungen, wie die log-normale oder die gestreckte Exponentialverteilung, können in einem kleinen Bereich wie ein Potenzgesetz aussehen, vor allem in einem Log-Log-Diagramm. Das führt oft zu falschen Ergebnissen, wo wir es als Potenzgesetz ansehen, nur weil die Grafik „linear aussieht“.Ein weiteres Problem ist die zu starke Verallgemeinerung. Viele Leute denken, dass Potenzgesetze alles über ein System erklären, aber sie erklären vielleicht nur einen kleinen Teil davon, meistens die Extreme. Zum Beispiel könnte die obersten 1 % der Leute eine bestimmte Machtgesetzmäßigkeit bei ihrer Einkommensverteilung haben, aber der Rest der Bevölkerung könnte eine ganz andere haben.

Das Gesetz des abnehmenden Ertrags ist ein weiteres Problem, mit dem reale Systeme zu kämpfen haben. Potenzgesetze sagen, dass extreme Ergebnisse möglich sind, aber in manchen Bereichen, wie zum Beispiel bei physikalischen Grenzen oder regulatorischen Rahmenbedingungen, gibt es Grenzen, ab denen das Modell nicht mehr funktioniert. Wenn du denkst, dass das Tail-Verhalten ewig so weitergeht, könntest du denken, dass die Risiken oder Chancen größer sind, als sie wirklich sind, vor allem in Systemen mit Grenzen.

Fazit

Potenzgesetze helfen uns, Systeme zu verstehen, in denen wenige extreme Ereignisse oder Einheiten einen großen Einfluss haben, wie zum Beispiel Erdbeben, Internetverkehr oder die Verteilung von Einkommen. In diesem Tutorial haben wir gelernt, was Potenzgesetze so besonders macht, welche mathematischen Eigenschaften und empirischen Merkmale sie haben, wie man sie findet und überprüft und wo man sie in der realen Welt findet.

Die Potenzgesetzanalyse wird in Zukunft in Bereichen wie KI, Wirtschaft, Netzwerkwissenschaft und Risikomanagement interessant sein. Mit den richtigen Tools und dem richtigen Wissen können wir sie nutzen, um eine komplizierte, nichtlineare Welt besser zu verstehen.

Wenn du dich mit echten Daten beschäftigst, frag dich immer: Ist das Seltene wirklich selten – oder ist es nur stark verteilt?

Wenn du mehr über einige der Konzepte erfahren möchtest, schau dir bitte die folgenden Ressourcen an:

• Einführung in die Wahrscheinlichkeitsregeln – Spickzettel
• Leitfaden zu Big-O-Notation und Zeitkomplexität
• Allgemeine lineare Modelle in Python