Loi de puissance : Une tendance derrière les événements extrêmes

Vous êtes-vous déjà demandé pourquoi quelques sites web génèrent la majeure partie du trafic Internet ? Ou pourquoi une petite fraction d'individus contrôle-t-elle la majorité des richesses mondiales ? La réponse réside dans un phénomène statistique fascinant appelé « loi de puissance ». 

Les lois de puissance régissent de nombreux systèmes naturels et artificiels. Ces distributions sont particulières car elles ne varient pas en fonction de l'échelle et présentent des queues lourdes. Ces caractéristiques les rendent idéales pour modéliser des données où de petits événements se produisent fréquemment, mais où les événements importants, même s'ils sont rares, ne peuvent être ignorés.

Ce tutoriel vous fournira un aperçu complet des lois de puissance, y compris leur théorie, leurs mathématiques, leurs utilisations et la manière de les estimer. Nous examinerons comment ils sont invariants à l'échelle et pourquoi ils apparaissent dans divers domaines tels que la géophysique, la finance, la biologie et l'Internet.

Propriétés des distributions de loi de puissance

Commençons par ce qui rend les lois de puissance particulières et en quoi elles diffèrent des distributions que vous avez pu utiliser jusqu'à présent. 

Caractéristiques des lois de puissance. Source : Serviette AI

Invariance d'échelle et autosimilarité

En termes simples, l'invariance d'échelle implique que si vous zoomez ou dézoomez, le motif de la distribution reste le même. 

En termes statistiques, une distribution de loi de puissance présente la même forme fonctionnelle quelle que soit l'échelle à laquelle on l'observe. Si une variable suit une loi de puissance, la multiplier par une constante ne modifie pas sa distribution, mais uniquement son échelle.

Mathématiquement, cela signifie que :

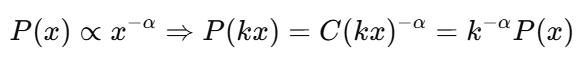
Cela diffère considérablement des autres distributions courantes, telles que la distribution normale, où laforme est définie en fonction de certains paramètres clés comme la moyenne et l'écart type.

Cette propriété est également similaire à l'auto-similarité, qui est une caractéristique clé des fractales. Les fractales sont des structures qui ont toujours le même aspect, quel que soit le niveau de zoom. Par exemple, si vous zoomez sur n'importe quelle partie d'un flocon de neige, d'une feuille de fougère ou d'une branche d'arbre, vous verrez une version réduite de l'ensemble. 

Une côte semble identique à 10 mètres de distance qu'à 10 kilomètres. 

Les lois de puissance illustrent parfaitement cette structure répétitive. C'est pourquoi ils sont utiles lorsque l'on examine des systèmes dont la taille, la fréquence ou l'intensité varient considérablement, mais suivent toujours le même schéma.

Queues lourdes et absence d'échelle caractéristique

La plupart des distributions classiques (telles que gaussiennes ou exponentielles) diminuent rapidement dans les queues. Ce n'est pas le cas des lois de puissance. Ils présententdes queues lourdes d' , ce qui signifie que la probabilité d'événements extrêmes est plus élevée.

Dans la vie réelle, les tremblements de terre importants, les tweets viraux et les milliardaires sont tous des exemples d'événements rares qui ont néanmoins une chance de se produire. En réalité, pour certaines valeurs d'alpha, des moments tels que la moyenne ou la variance peuvent même ne pas exister, et c'est pourquoi nous affirmons que les distributions de loi de puissance n'ont pas d'échelle. 

Universalité et incomplétude statistique

L'une des caractéristiques remarquables des lois de puissance est leur universalité ; elles peuvent être observées dans des systèmes qui ne semblent présenter aucune corrélation entre eux. Voici quelques exemples : magnitude des tremblements de terre, pics d'activité neuronale, taille des entreprises et fréquence des mots. 

Le revers de la médaille est qu'elles sont également incomplètes sur le plan statistique. Cela signifie que même si nous pouvons modéliser le comportement de la queue, il est difficile d'estimer un ensemble complet de statistiques sommaires, en particulier à partir de petits échantillons de données. 

Fondements mathématiques des lois de puissance

Explorons plus en détail les calculs mathématiques qui rendent les lois de puissance à la fois puissantes et complexes.

Forme fonctionnelle et propriétés d'échelle

La forme standard d'une loi de puissance est la suivante :

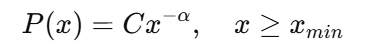
Où :

• alpha est l' exposant de mise à l'échelle
• C est la constante de normalisation
• x_min​ est leseuil d' e au-delà duquel la loi de puissance s'applique.

À mesure que l'alpha augmente, la queue devient plus fine. Un alpha faible signifie que les événements sont plus extrêmes. Cet exposant de mise à l'échelle régit tout, de l'inégalité à la taille des écosystèmes.

Distributions de probabilité selon une loi de puissance et graphiques logarithmiques

La première étape consiste à utiliser un graphique log-log pour détecter une loi de puissance dans des ensembles de données réels.

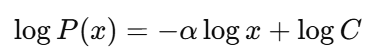
Si les données suivent effectivement une loi de puissance, vous obtiendrez une ligne droite avec une pente de −α. Cependant, soyez prudent, car de nombreuses distributions semblent linéaires sur un graphique logarithmique. 

Relations avec d'autres distributions

Il existe plusieurs distributions statistiques importantes qui sont similaires aux lois de puissance.

• Les distributions de Pareto, souvent utilisées en économie, illustrent la répartition de la richesse et des revenus, où une minorité de personnes détient la majeure partie des ressources. Il s'agit d'un exemple précoce et classique de la loi de puissance en action.
• La loi de Zipf explique comment la fréquence des mots dans le langage naturel suit une loi de puissance. Par exemple, le deuxième mot le plus fréquent apparaît environ deux fois moins souvent que le mot le plus fréquent, le troisième environ trois fois moins souvent, et ainsi de suite.
• La distribution zeta est une version discrète de la loi de puissance qui est souvent utilisée pour modéliser des phénomènes fréquents, tels que les visites sur un site web ou les ventes de livres.

Parfois, les données du monde réel ne suivent pas toujours une loi de puissance « pure ». Dans ces situations, nous observons des coupures exponentielles (où les valeurs très élevées deviennent moins probables), des lois de puissance courbes ou des queues log-normales. Ces modèles sont plus adaptés aux systèmes présentant des limites physiques ou pratiques. Ces hybrides savent que l'invariance d'échelle peut fonctionner pour une partie de la gamme, mais qu'elle finira par ne plus fonctionner.

Manifestations empiriques dans différentes disciplines

Les lois de puissance ne sont pas seulement des concepts mathématiques ; elles se manifestent dans le monde réel et nous aident à comprendre des systèmes qui semblent aléatoires ou chaotiques à première vue.

Systèmes naturels et géophysiques

Les lois de puissance nous aident à comprendre les événements extrêmes dans la nature. Par exemple, la loi de Gutenberg-Richter stipule que les magnitudes des tremblements de terre suivent une distribution de loi de puissance. Cela signifie que de petites secousses se produisent fréquemment, mais que leur nombre diminue rapidement à mesure que la magnitude du séisme augmente. C'est pourquoi un séisme de magnitude 2,0 peut se produire tous les jours, mais un séisme de magnitude 7,0 peut ne pas se produire pendant des années. Les deux font partie du même constat statistique. 

De la même manière, les réseaux fluviaux, les côtes et même les coups de foudre présentent des motifs fractals auto-similaires qui suivent une loi de puissance dans la taille de leurs segments.

Les lois de puissance s'appliquent également à l'univers. En astrophysique, nous observons que la taille des étoiles, la distribution des trous noirs et même les amas de galaxies présentent tous des queues lourdes. Il existe des milliards de petites étoiles, mais seules quelques-unes, particulièrement imposantes, se distinguent dans la galaxie. Cette inégalité peut sembler aléatoire, mais une fois que l'on comprend la loi de puissance qui se cache derrière, on constate qu'elle obéit à certaines règles statistiques.

Systèmes socio-économiques et biologiques

Lorsqu'on examine les inégalités et les échelles dans les sociétés humaines, les lois de puissance sont particulièrement utiles. Nous avons déjà abordé la distribution de Pareto dans la section précédente. Il ne s'agit pas seulement d'une théorie économique : elle s'observe également dans les déclarations fiscales, les bénéfices des entreprises et les habitudes en matière de dons. 

Les 1 % des personnes les plus riches suivent la loi de Pareto, et non les moyennes gaussiennes. Ces distributions ne correspondent pas à une courbe en cloche bien définie ; elles s'étendent plutôt vers la droite, présentant quelques valeurs extrêmes (comme les milliardaires) qui font grimper la moyenne.

Les lois de puissance révèlent également des schémas cachés en biologie. Par exemple, la loi de Kleiber stipule que le taux métabolique d'un animal augmente proportionnellement au cube de sa masse corporelle, et non de manière linéaire. Cela nous aide à comprendre pourquoi un éléphant ne mange pas mille fois plus qu'un lapin, même s'il pèse mille fois plus lourd. 

Les lois de puissance s'appliquent également à la population des villes, aux taux de croissance des entreprises, au comportement électoral et même aux décès dans les conflits, où quelques éléments ou événements majeurs ont un effet disproportionné.

Technologie et commerce

Les lois de puissance sont ce qui permet au monde numérique de fonctionner et de prospérer. Réfléchissez au fonctionnement du trafic sur Internet : seuls quelques sites (tels que Google, Facebook et YouTube) reçoivent la plupart des visites, tandis que des millions d'autres pages passent pratiquement inaperçues. Il s'agit d'un comportement typique de la longue traîne, particulièrement important dans des domaines tels que le référencement naturel (SEO), les moteurs de recommandation et le marketing numérique.

Dans le domaine de l'IA, la taille et les performances des modèles ont tendance à évoluer dans le même sens. Il existe quelques grands modèles, tels que GPT-4, qui sont les meilleurs dans leur domaine, mais des centaines de modèles plus petits ne peuvent pas suivre le rythme. Cette concentration s'explique en partie par des boucles de rétroaction : les modèles plus performants attirent davantage d'utilisateurs, de données et de fonds, ce qui les rend encore plus puissants. 

Estimation statistique et validation

Il semble donc que votre ensemble de données obéisse à une loi de puissance. L'histogramme peut présenter une longue queue, ou le graphique log-log peut afficher une ligne presque droite. C'est un bon début, mais il ne suffit pas de se limiter à cette observation, car il est facile de se laisser induire en erreur par les lois de puissance. C'est pourquoi nous avons besoin de bons outils statistiques pour déterminer les paramètres et vérifier l'adéquation.

Méthodes d'estimation des paramètres

L'exposant d'échelle, généralement noté 𝛼, est le premier élément nécessaire pour modéliser correctement une distribution de loi de puissance. 

L'estimation du maximum de vraisemblance (EMV) est l'une des méthodes les plus courantes pour obtenir une estimation de 𝛼. Il s'agit d'une méthode permettant de déterminer les valeurs des paramètres qui rendent les données observées les plus probables dans l'ensemble des statistiques.

Pour les données continues avec une valeur minimale connue 𝑥min, voici comment cela fonctionne :

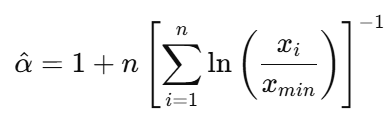
• 𝑥𝑖 sont les valeurs que vous avez observées, et elles sont toutes supérieures ou égales à 𝑥𝑚𝑖𝑛.
• 𝑛 est le nombre d'observations.

Cependant, voici la partie difficile : il est essentiel de choisir la bonne valeur 𝑥 min. Si elle est trop faible, votre modèle contient des données qui ne suivent pas vraiment la loi de puissance. Et si elle est trop élevée, vous finirez par gaspiller trop de données. De plus, lorsque les échantillons sont de petite taille, les estimations MLE peuvent être peu fiables.

Test d'adéquation

Après avoir estimé l'exposant, la question suivante est la suivante : dans quelle mesure convient-il ? On ne peut pas simplement dire : « Cela ressemble un peu à une loi de puissance. » Vous avez besoin de preuves statistiques démontrant que la loi de puissance explique mieux vos données que d'autres distributions possibles. C'est là qu'intervient le test de Kolmogorov-Smirnov (KS). Ce test identifie l'écart le plus important entre la fonction de distribution cumulative (CDF) de vos données observées et le modèle théorique de loi de puissance. 

Plus ce nombre est proche de zéro, plus votre modèle correspond aux données. Le test KS n'utilise pas de binning ni d'histogrammes comme le font de nombreux autres tests. Au lieu de cela, il fonctionne directement avec les données brutes, ce qui le rend très utile pour les distributions à queue lourde.Cependant, une loi de puissance n'est pas toujours la seule explication plausible. Une distribution log-normale ou exponentielle pourrait également permettre de modéliser vos données. C'est dans ce cas queles tests du rapport de vraisemblance d' s'avèrent utiles. Le principe est simple : utiliser l'estimation maximale de vraisemblance (MLE) pour ajuster les deux modèles aux mêmes données, déterminer les vraisemblances, puis les comparer. Vous disposez d'un soutien statistique pour le modèle de loi de puissance si sa probabilité est nettement plus élevée. 

Le cadre Clauset-Shalizi-Newman (2009) est l'un des nombreux outils qui combinent l'estimation maximale de vraisemblance, le test de KS et les tests du rapport de vraisemblance pour constituer une méthode efficace d'analyse du comportement des lois de puissance.

Mécanismes théoriques et modèles génératifs

Maintenant que nous savons où les lois de puissance apparaissent dans le monde réel et comment les trouver statistiquement, la question suivante est la suivante : pourquoi ces distributions apparaissent-elles en premier lieu ? Examinons comment les lois de puissance peuvent émerger de la dynamique des systèmes.

Attachement préférentiel et processus de Yule

Le modèle Barabási-Albert (1999) a introduit le concept d'attachement préférentiel, souvent résumé par le phénomène « les riches s'enrichissent ». C'est l'un des exemples les plus connus et les plus faciles à comprendre du fonctionnement des lois de puissance. 

Envisagez de créer un réseau, tel qu'Internet ou un site de réseau social. Lorsqu'un nouvel utilisateur rejoint le réseau, il est plus susceptible de se connecter à des nœuds populaires tels que Facebook ou Google, car ces nœuds sont déjà bien connus. 

Au fil du temps, cela crée une boucle de rétroaction : les nœuds populaires obtiennent encore plus de connexions, tandis que les nœuds plus récents ou moins connectés restent petits. Cela crée un réseau sans échelle où les degrés des nœuds suivent une loi de puissance.

De même, les processus de Yule modélisent la croissance des genres biologiques, ce qui constitue une extension de cette idée. Dans ce modèle, les espèces qui comptent déjà un plus grand nombre d'individus sont plus susceptibles de donner naissance à de nouvelles espèces. Cela conduit à une distribution asymétrique où quelques genres dominent.

Modèles de croissance aléatoire, loi de Gibrat et processus de Markov

Les processus de croissance aléatoire constituent un autre exemple de l'application des lois de puissance. L'idée principale est que les choses deviennent plus importantes au fil du temps en multipliant des quantités aléatoires plutôt qu'en les additionnant. 

La loi de Gibrat stipule que le taux de croissance est indépendant de la taille. La plupart des choses restent petites, mais quelques-unes grandissent très rapidement et deviennent très importantes, formant ainsi la longue traîne d'une loi de puissance. 

Les processus de Markov, en particulier ceux impliquant un bruit multiplicatif, peuvent également converger vers des distributions stationnaires de type loi de puissance, notamment dans le cas de frontières réfléchissantes.

Il existe également un aspect probabiliste à cela. Les processus de Markov peuvent également présenter un comportement de loi de puissance dans certaines situations. Ces processus modélisent des systèmes dans lesquels l'état suivant dépend uniquement de l'état actuel, et non du passé. Les gens ont utilisé ce modèle pour représenter des phénomènes tels que les déplacements d'une population ou le fonctionnement des files d'attente.

Ces modèles ne sont pas seulement des idées intéressantes. Ils nous aident à comprendre comment les systèmes complexes évoluent au fil du temps, pourquoi les inégalités persistent et comment les effets de réseau influencent tous les domaines, de la biologie à la blockchain. Non seulement nous pouvons utiliser les lois de puissance pour décrire le monde, mais nous pouvons également les utiliser pour l'expliquer.

Implications, limites et applications

Il est essentiel de comprendre la dynamique des lois de puissance, car cela peut avoir un impact considérable sur vos prévisions et vos choix, que vous élaboriez un modèle de risque financier, gériez une infrastructure Internet ou étudiiez les comportements sociaux. 

Considérations pratiques

Les modèles de loi de puissance sont utiles pour les systèmes où des événements rares mais importants se produisent. Par exemple, dans le domaine financier, les prix peuvent évoluer à un rythme normal la plupart du temps, mais les « cygnes noirs » – ces rares effondrements ou booms – peuvent avoir un impact considérable. 

Les modèles basés sur la loi de puissance permettent de mieux appréhender ce risque extrême que les modèles traditionnels, qui sous-estiment souvent la probabilité que ces événements se produisent. Pour la gestion des risques, l'assurance, la cybersécurité et la planification en cas de catastrophe, c'est très important.

Il est également avantageux de comprendre la croissance non linéaire et les effets cumulatifs. Les lois de puissance permettent d'expliquer pourquoi certaines personnes, entreprises ou nœuds d'un réseau peuvent devenir les plus puissants au fil du temps et pourquoi ces situations de « gagnant-gagne » ne sont pas seulement inhabituelles, mais normales dans ce type de systèmes.

Cependant, les modèles basés sur la loi de puissance présentent certains inconvénients. L'un des problèmes est qu'ils défient l'intuition, dans le sens où ils ne présentent pas toujours des moyennes ou des variances claires, ce qui rend difficile la détermination de mesures courantes telles que la « valeur attendue » ou l'« écart type ».

Ces modèles ne fonctionnent généralement que sur la queue de la distribution, ils peuvent donc ne pas convenir à la majeure partie des données, voire à aucune. Cela peut poser problème si vous ne faites pas attention à l'endroit où commence réellement le comportement de la loi de puissance.

Limites et critiques

Tous les ensembles de données présentant des queues longues ne suivent pas nécessairement une loi de puissance réelle. Peu de distributions, telles que la distribution log-normale ou exponentielle étirée, peuvent ressembler à une loi de puissance dans une petite plage, en particulier sur un graphique log-log. Cela conduit souvent à des faux positifs, où nous considérons qu'il s'agit d'une loi de puissance simplement parce que le graphique « semble linéaire ».La généralisation excessive est un autre problème. On pense souvent que les lois de puissance expliquent tout d'un système, mais elles n'en expliquent souvent qu'une petite partie, généralement les extrêmes. Par exemple, les 1 % les plus riches peuvent avoir une loi de distribution des revenus, mais le reste de la population peut avoir une loi très différente.

La loi des rendements décroissants est un autre problème auquel sont confrontés les systèmes réels. Les lois de puissance indiquent que des résultats extrêmes sont possibles, mais dans certains domaines, tels que les limites physiques ou les environnements réglementaires, il existe des limites au-delà desquelles le modèle ne fonctionne plus. Si vous pensez que le comportement de la queue se poursuit indéfiniment, vous pourriez estimer que les risques ou les avantages sont plus importants qu'ils ne le sont réellement, en particulier dans les systèmes comportant des limites.

Conclusion

Les lois de puissance nous aident à comprendre les systèmes dans lesquels quelques événements ou entités extrêmes ont un impact considérable, comme les tremblements de terre, le trafic Internet ou la répartition des revenus. Dans ce tutoriel, nous avons découvert ce qui différencie les lois de puissance, leurs propriétés mathématiques et leurs empreintes empiriques, comment les identifier et les vérifier, ainsi que les domaines dans lesquels elles peuvent être observées dans le monde réel.

L'analyse des lois de puissance aura des applications futures intéressantes dans des domaines tels que l'intelligence artificielle, l'économie, la science des réseaux et la gestion des risques. Nous pouvons les utiliser pour mieux comprendre un monde complexe et non linéaire si nous disposons des outils et des connaissances adéquats.

Lorsque vous explorez en profondeur des données réelles, posez-vous toujours la question suivante : ce qui est rare est-il vraiment rare, ou simplement très dispersé ?

Si vous souhaitez en savoir plus sur certains concepts, veuillez consulter les ressources suivantes :

• Fiche récapitulative des règles de probabilité
• Guide sur la notation O grand et la complexité temporelle
• Modèles linéaires généralisés en Python