Como calcular o desvio padrão no Excel

Vários conceitos e métodos estatísticos importantes, como variância, coeficiente de variação e intervalos de confiança, dependem do desvio padrão como medida fundamental de variabilidade, tornando-o uma das ferramentas mais importantes em estatística que os profissionais de dados devem dominar.

Se, ao ler este artigo, você perceber que quer dar uma repassada em estatística, faça nosso curso Introdução à Estatística, que aborda vários tópicos básicos sem precisar programar.

Como calcular o desvio padrão no Excel

Para calcular o desvio padrão no Excel, insira seus dados em uma coluna e use a função STDEV.P() função para uma população ou a STDEV.S() para uma amostra.

A principal diferença entre essas funções é que STDEV.P() divide pelo número total de pontos de dados, enquanto STDEV.S() divide pelo número de pontos de dados menos um (n-1) para levar em conta a variabilidade da amostra.

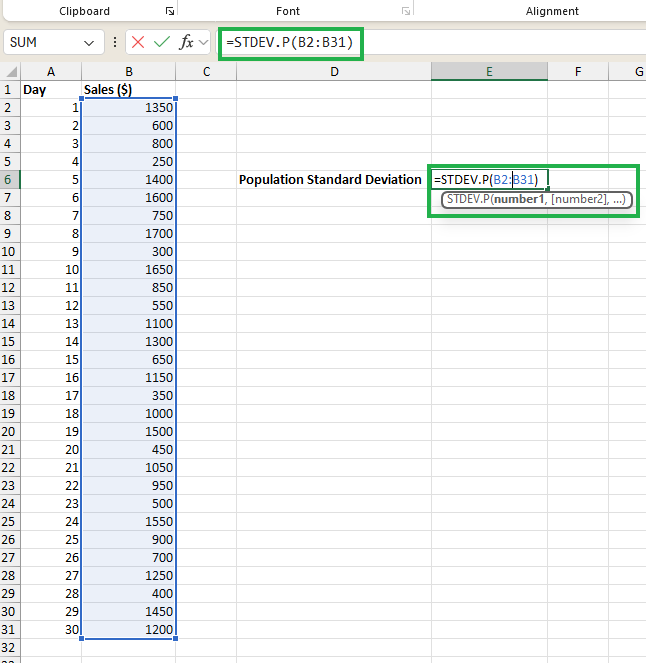
Cálculo rápido do desvio padrão no Excel. Imagem do autor.

Por exemplo, se seus dados estiverem nas células B2 a B31, digite =STDEV.P(B2:B31) para calcular o desvio padrão da população ou =STDEV.S(B2:B31) para o desvio padrão da amostra. O Excel vai calcular e mostrar automaticamente o desvio padrão do seu conjunto de dados.

População vs. Desvio padrão da amostra no Excel

O desvio padrão é uma medida estatística que mostra o quanto os números variam ou se espalham em um conjunto de valores numéricos. Mostra o quanto os valores num conjunto de dados se afastam da média (média) do conjunto de dados. 

Isso ajuda a entender o quanto os dados variam — um desvio padrão baixo mostra que os valores estão próximos da média, o que sugere consistência, enquanto um desvio padrão alto indica mais variação, o que sugere dados mais espalhados.

STDEV.P() para o desvio padrão da população

A fórmula para o desvio padrão depende se estamos lidando com uma população ou uma amostra. A fórmula para o desvio padrão da população (σ) é a seguinte:

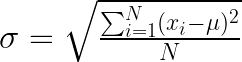
Desvio padrão da população. Imagem do autor.

Onde:

• N é o número total de pontos de dados na população.

• x_i​ representa cada ponto de dados individual.

• μ é a média (média) da população.

Essa fórmula calcula a média dos desvios quadrados da média e, em seguida, tira a raiz quadrada dessa média.

A funçãoSTDEV.P() no Excel calcula o desvio padrão para toda uma população. Essa função assume que os argumentos fornecidos incluem toda a população. A sintaxe da função STDEV.P() função é a seguinte:

STDEV.P(number1, [number2], ...)

Os parâmetros são:

• number1: O primeiro número é tipo uma população.

• [number2], ...: Números ou referências adicionais opcionais que correspondem a uma população, até 254 argumentos.

STDEV.P() calcula o desvio padrão usando a fórmula do desvio padrão populacional que aprendemos antes. Isso garante que o cálculo reflita as características de toda a população.

A gente deve usar a análise de variação ( STDEV.P() ) quando tem dados que representam toda a população. Por exemplo, ao analisar as notas dos exames de todos os alunos de uma escola específica, a análise de correlação ( STDEV.P() ) é a mais indicada, porque o conjunto de dados inclui toda a população de interesse.

STDEV.S() para o desvio padrão da amostra

A fórmula para o desvio padrão da amostra (s) é a seguinte. Observe que, para o desvio padrão da amostra, usamos a letra minúscula n por convenção.

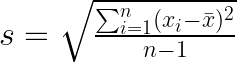
Exemplo de equação do desvio padrão. Imagem do autor.

Onde:

• n é o número total de pontos de dados na amostra.

• x_i​ representa cada ponto de dados individual.

• xˉ é a média da amostra.

A fórmula é parecida com a do desvio padrão da população. Mesmo assim, usa a correção de Bessel ( n - 1 ) no denominador pra levar em conta que uma amostra tá sendo usada pra estimar o parâmetro da população. Essa correção faz com que o desvio padrão da amostra seja um estimador imparcial do desvio padrão da população.​

A funçãoSTDEV.S() no Excel calcula o desvio padrão para uma amostra da população. Essa função assume que os argumentos fornecidos são uma amostra da população, e não a população inteira. A sintaxe da função STDEV.S() função é a seguinte:

STDEV.S(number1, [number2], ...)

Os parâmetros são:

• number1: O primeiro argumento numérico é uma amostra da população.

• [number2], ...: Números ou referências adicionais opcionais que correspondem a uma amostra, até 254 argumentos.

STDEV.S() calcula o desvio padrão usando a fórmula para o desvio padrão amostral, levando em conta a correção de Bessel, como aprendemos anteriormente.

Na prática, quando a gente tem uma amostra de dados, usa STDEV.S() para estimar o desvio padrão de toda a população. Digamos que analisamos as notas de um grupo de alunos escolhidos aleatoriamente numa escola. A análise de dados de amostra ( STDEV.S() ) é a melhor opção, porque nosso conjunto de dados é só uma amostra do total de alunos.

Agora que aprendemos sobre as funções disponíveis no Excel para calcular o desvio padrão, vamos colocar todo o nosso conhecimento em prática usando um exemplo.

Trabalhando com um exemplo de desvio padrão no Excel 

Calculando o desvio padrão no Excel 

Imagina um cenário em que, como analista de dados, você precisa analisar o desempenho de vendas de uma pequena loja de varejo. O dono da loja quer entender como as vendas diárias variaram no último mês pra gerenciar melhor o estoque e o número de funcionários. 

Você coletou os dados de vendas diárias por 30 dias e precisa calcular o desvio padrão para ver como as vendas variam. 

Vamos começar tabulando os registros em uma coluna, digamos B2 a B31, em uma planilha do Excel.

Armazena o conjunto de dados de vendas das lojas. Imagem do autor.

A gente pode calcular o desvio padrão da população na célula E6 digitando a seguinte equação:

=STDEV.P(B2:B31)

Você vai ver o desvio padrão da população calculado na célula E6 assim:

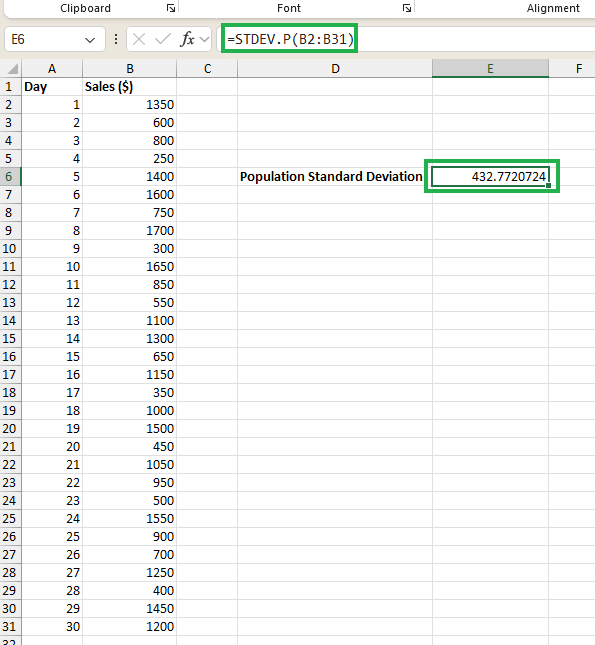
Calculando o desvio padrão da população. Imagem do autor.

Usamos a função STDEV.P() porque, no nosso caso, toda a nossa população para a análise são os dados de vendas do último mês.

Digamos que a gente está fazendo uma análise de um ano inteiro usando os dados dos últimos 30 dias como amostra; então, vamos usar a STDEV.S() função como mostrado na equação abaixo:

=STDEV.S(B2:B31)

E vamos ver o desvio padrão calculado da amostra abaixo:

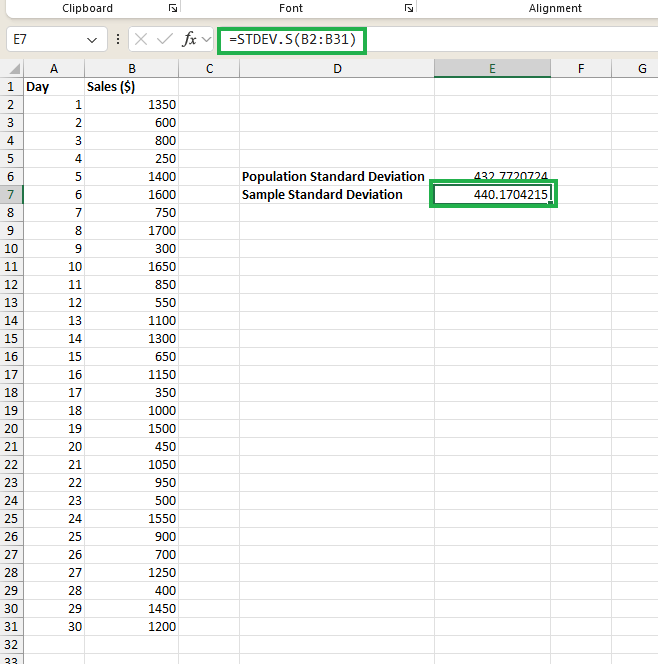
Calculando o desvio padrão da amostra. Imagem do autor.

Depois de calcular o desvio padrão, o próximo passo é interpretar o resultado num contexto empresarial. 

Interpretando os valores do desvio padrão

Pra entender melhor os valores do desvio padrão e complementar nossa análise, dá pra calcular a média dos dados de vendas usando a equação abaixo:

=AVERAGE(B2:B31)

O valor médio pode ser calculado como $975 na célula E7, como mostrado abaixo:

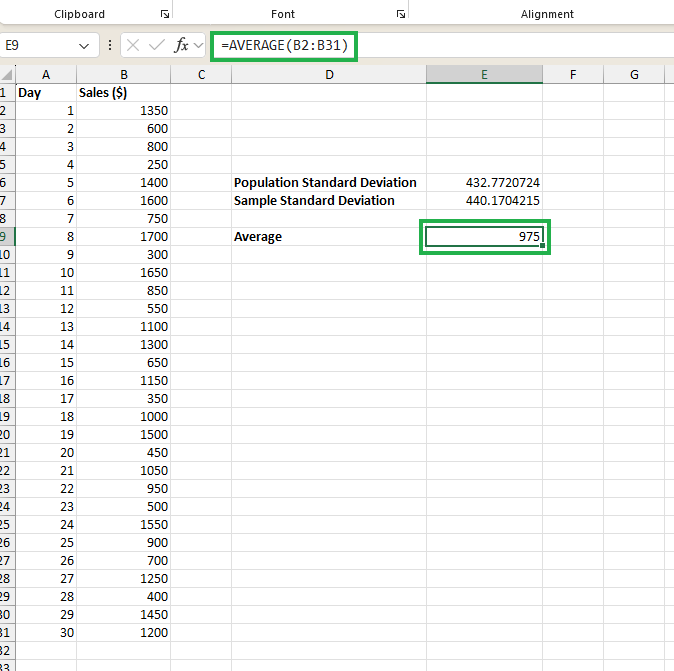
Calculando a média do conjunto de dados. Imagem do autor.

Junto com o valor médio que a gente conseguiu, dá pra interpretar os valores do desvio padrão como:

• Desvio padrão da população: O desvio padrão da população de aproximadamente 432,77 mostra que, em média, as vendas diárias variam em cerca de $432,77 em relação ao valor médio das vendas de $975. Esse número mostra como os dados de vendas se espalharam, já que a gente considerou o mês inteiro como um conjunto completo de dados.
• Desvio padrão da amostra: O desvio padrão da amostra de aproximadamente 440,17 é um pouco maior do que o desvio padrão da população. Esse valor é importante se a gente estiver considerando os 30 dias de dados como uma amostra de uma população maior (por exemplo, todos os meses futuros possíveis).
• Desvio padrão da amostra mais alto: O valor um pouco mais alto no desvio padrão da amostra explica a incerteza em usar uma amostra para estimar a variabilidade geral nas vendas. Isso sugere que, se analisarmos outro mês, podemos esperar uma variação parecida nas vendas diárias.
• Grande variação nas vendas: Os dois valores de desvio padrão mostram que as vendas diárias variam bastante, ou seja, os números tendem a mudar bastante em relação à média de $975. Esse nível de variabilidade pode afetar a gestão de estoque e a contratação de pessoal. Em alguns dias, as vendas podem ser bem maiores ou menores do que a média, o que pode levar a um excesso ou falta de estoque se não for bem gerenciado.

Como os valores do desvio padrão mostram que as vendas diárias não são consistentes e variam bastante, dá pra fazer uma análise mais detalhada ou criar um modelo de machine learning pra estimar as vendas em um dia específico.

O dono da loja deve pensar nessa variação ao planejar o estoque e a equipe para evitar possíveis problemas relacionados ao excesso de estoque ou falta de pessoal.

Como adicionar barras de desvio padrão no Excel

Adicionar barras de desvio padrão aos nossos gráficos no Excel é uma maneira útil de mostrar a variação dos nossos dados. 

Selecione o intervalo de dados, B2 a B31, do nosso exemplo e vá para a Inserir. Escolha o tipo de gráfico que você quer, como mostra a imagem abaixo (por exemplo, gráfico de linhas), e insira o gráfico.

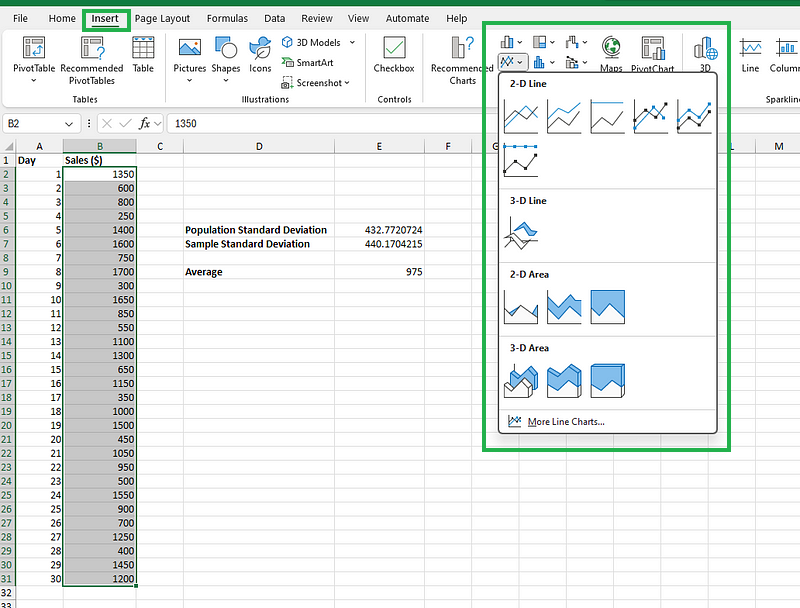
Inserindo um gráfico com os dados de vendas da loja. Imagem do autor.

Você vai ver um gráfico de linhas simples abaixo:

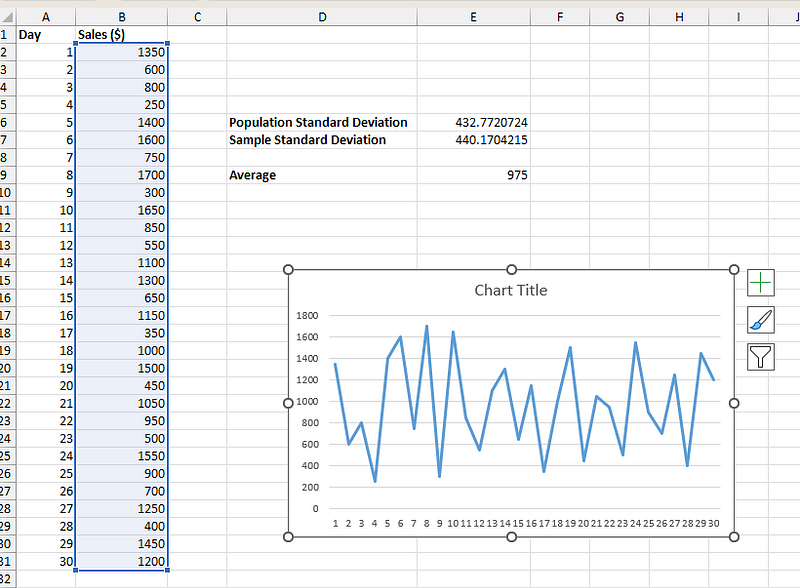
Gráfico de linhas para dados de vendas da loja. Imagem do autor.

Clique na série de dados no seu gráfico para destacá-la. Essa etapa é necessária para adicionar barras de erro à série de dados selecionada. Vá para o Gráfico Design que aparece quando você seleciona o gráfico. Clique em Adicionar Gráfico Elemento (que tá no grupo Layouts do gráfico ).

Depois, passa o mouse sobre Barras de erro Barras e selecione Padrão Desvio para adicionar as barras de desvio padrão ao gráfico de linhas.

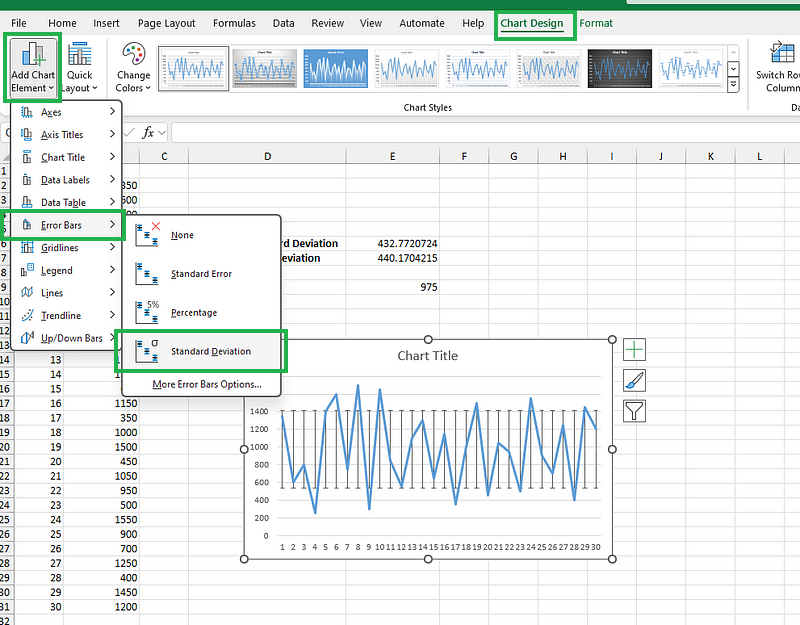
Adicionando barras de desvio padrão ao gráfico de linhas. Imagem do autor.

Você também pode passar o mouse Erro Barras e clicar em Mais Barras Barras Opções para formatar melhor as barras de erro e ajustar a cor, a largura e o estilo da linha de acordo com as preferências de design do seu gráfico. Isso pode ser feito no mesmo painel, nas opções“ ” (Formato) e “Format Error Bars” (Formatar barras de erro). Fique à vontade para brincar com o gráfico até conseguir o gráfico que você quer visualizar.

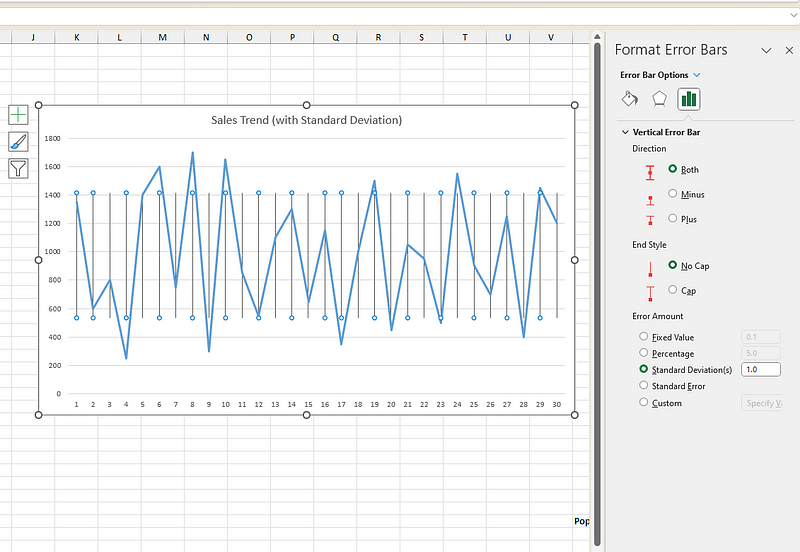
Formatação das barras de desvio padrão. Imagem do autor.

Adicionar barras de desvio padrão aos nossos gráficos no Excel dá uma visão clara da variação nos dados, o que ajuda na análise eficaz dos dados e na tomada de decisões.

Conclusão

O desvio padrão é uma ferramenta fundamental e valiosa que nos ajuda a entender a variabilidade de um conjunto de dados. Além disso, é usado em várias outras análises, como coeficiente de variação, intervalos de confiança e ANOVA, tornando-o uma técnica obrigatória para todos os profissionais de dados.

Recomendamos que você dê uma olhada no nosso programa prático e completo sobre Fundamentos do Excel para expandir ainda mais suas habilidades no Excel e na análise de dados.