Distribución de Weibull: Cómo modelar datos de tiempo hasta el evento

Cuando analizas la duración de las cosas (ya sea la vida útil de los componentes electrónicos, el tiempo de supervivencia de los pacientes o la fiabilidad de los equipos), necesitas una distribución que pueda manejar la complejidad de los patrones de fallo. La distribución de Weibull no asume que los fallos se producen a un ritmo constante, como hacen los modelos más simples. En cambio, puede modelar escenarios en los que las tasas de fallo aumentan con el tiempo (como los procesos de desgaste), disminuyen inicialmente (como los defectos de fabricación tempranos que se eliminan) o se mantienen estables.

Si los conceptos de probabilidad son nuevos para ti, nuestro curso Fundamentos de probabilidad en R cubrelos conceptos estadísticos básicos que necesitarás para realizar trabajos avanzados de distribución. Este tutorial te guiará a través de los fundamentos matemáticos de la distribución de Weibull. Aprenderás a estimar sus parámetros a partir de datos y verás cómo su flexibilidad lo hace especialmente útil en análisis de fiabilidad y estudios de supervivencia. Al final, comprenderás no solo la teoría que hay detrás de esta útil distribución, sino también cuándo y cómo aplicarla a tus propios retos de análisis del tiempo hasta el evento.

¿Qué es la distribución de Weibull?

La distribución de Weibull es una distribución de probabilidad continua diseñada para modelar datos de tiempo hasta un evento. Lo encontrarás con mayor frecuencia en análisis de fallos, estudios de supervivencia e ingeniería de fiabilidad, donde el objetivo es comprender «cuándo ocurre algo». 

Lo que diferencia a Weibull de otras alternativas más simples es su adaptabilidad a diferentes patrones de fallo. Mientras que algunas distribuciones asumen que los eventos ocurren a tasas constantes y predecibles, la distribución de Weibull puede manejar situaciones en las que la probabilidad de que ocurran los eventos cambia con el tiempo. Esta flexibilidad resulta útil cuando se trabaja con sistemas o procesos complejos cuyos mecanismos subyacentes no se comprenden del todo.

Contexto histórico y principios fundamentales

La historia detrás de esta distribución comienza con el matemático sueco Waloddi Weibull, quien la desarrolló en la década de 1930 mientras estudiaba la resistencia y la fatiga de los materiales. Tu trabajo sentó las bases de la ingeniería moderna de fiabilidad.

La distribución se presenta en dos formas principales que satisfacen diferentes necesidades analíticas. El modelo Weibull de dos parámetros utiliza parámetros de forma y escala para modelar escenarios en los que los eventos pueden comenzar de forma inmediata. La versión de tres parámetros añade un parámetro de ubicación, creando un umbral mínimo antes de que puedan producirse los eventos, lo que resulta útil para modelar sistemas con retrasos incorporados o períodos de «rodaje».

La distribución de Weibull pertenece a una familia de distribuciones relacionadas, en la que la distribución exponencial aparece como un caso especial. Esta conexión ayuda a explicar por qué a menudo se comparan los modelos de Weibull y exponencial en contextos de fiabilidad. La mayor flexibilidad de Weibull permite aproximarse a otras distribuciones bien conocidas en condiciones paramétricas específicas, lo que contribuye a su amplia adopción.

Parámetros de la distribución de Weibull

Ahora que ya hemos visto la evolución histórica y el comportamiento básico, exploremos los parámetros que confieren flexibilidad a la distribución de Weibull. Cada parámetro te proporciona información específica sobre cómo se comportan tus datos.

El parámetro de forma (k o β) controla el carácter de la distribución y el comportamiento de la función de riesgo. Cuando los valores son inferiores a 1, se observan patrones de mortalidad infantil en los que se producen fallos tempranos debido a defectos de fabricación. Cuando los valores son superiores a 1, se producen fallos por desgaste, es decir, las cosas se rompen por el uso habitual a lo largo del tiempo.

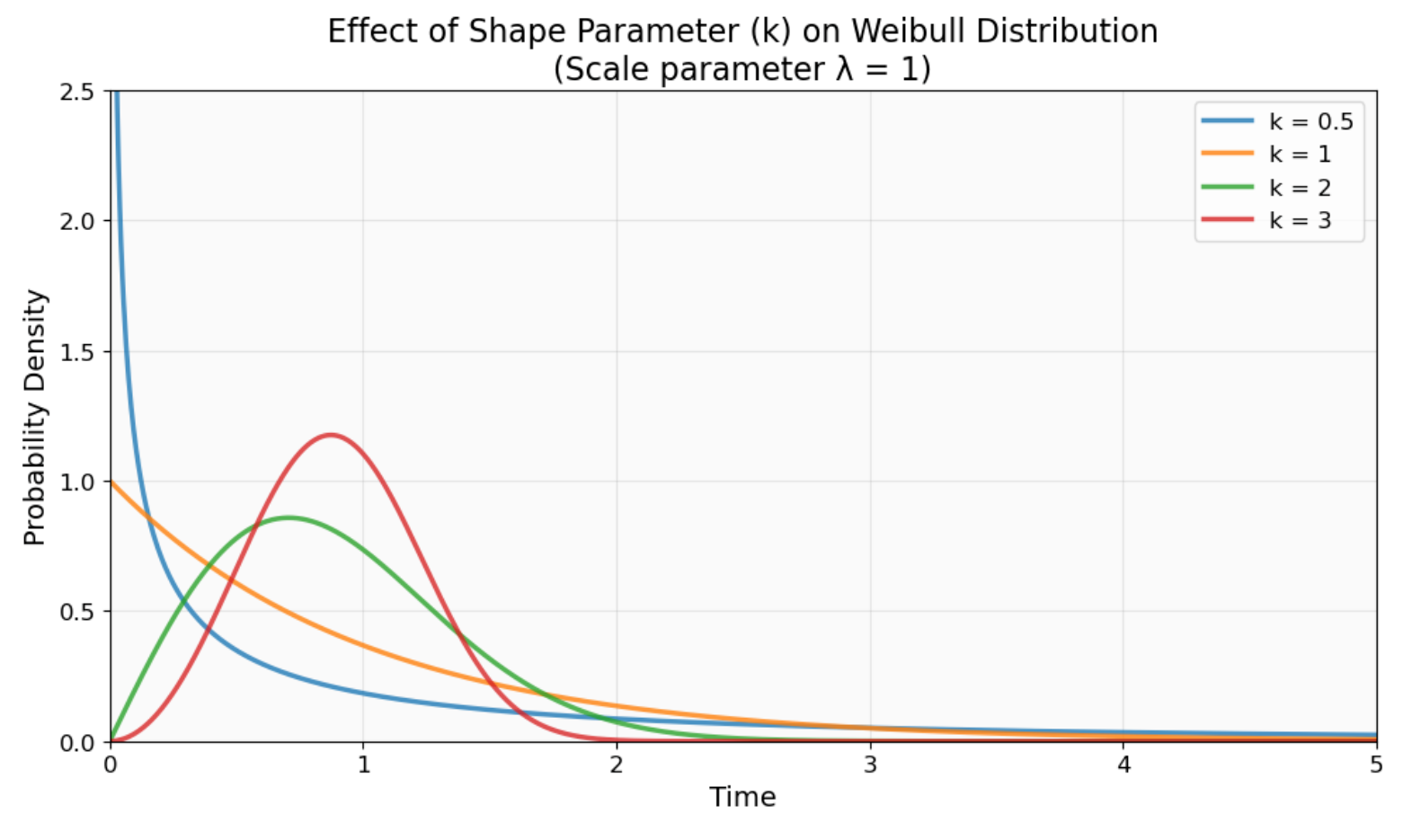
Efecto del parámetro de forma (k) en el comportamiento de la distribución de Weibull. Observa cómo k < 1 genera una alta probabilidad de fallo temprano (curva azul), k = 1 produce tasas de fallo constantes (naranja) y k > 1 muestra tasas de fallo crecientes con el tiempo (curvas verde y roja). Imagen del autor.

El parámetro de escala (λ o η) representa la vida característica. Este es el momento en el que exactamente el 63,2 % de los elementos habrán fallado, independientemente del valor del parámetro de forma. Puedes considerar esto como la vida útil típica de la distribución, aunque la media real puede diferir debido a la forma de la distribución.

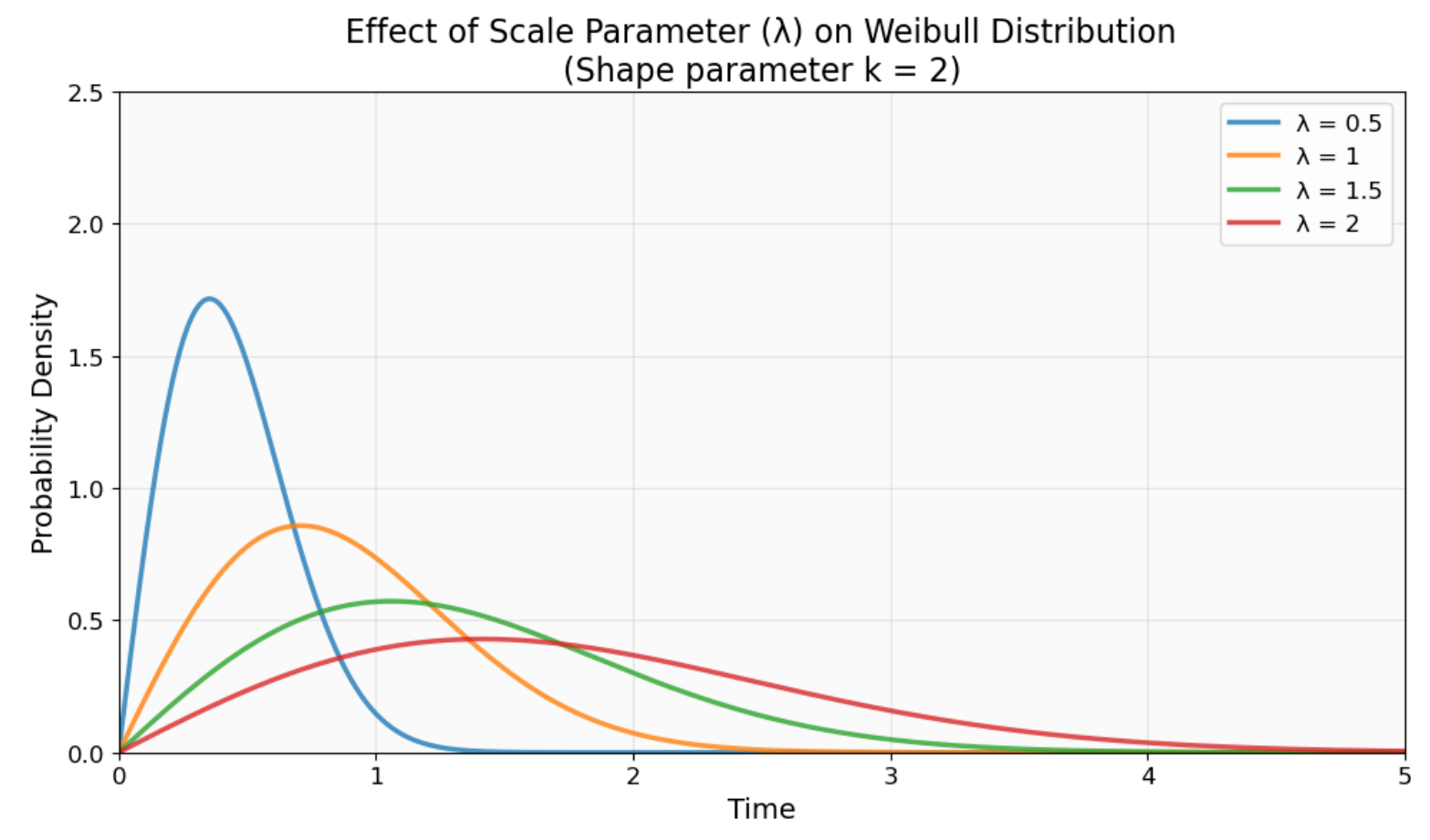
Cómo el parámetro de escala (λ) desplaza la distribución de Weibull a lo largo del eje temporal. Los valores más altos de λ estiran la distribución hacia la derecha (vida característica más larga), mientras que los valores más bajos la comprimen hacia la izquierda (vida característica más corta). La forma permanece constante. Imagen del autor.

En aplicaciones de tres parámetros, el parámetro de ubicación (θ o γ) desplaza la distribución a lo largo del eje temporal. Representa una vida útil mínima garantizada antes de que puedan comenzar a producirse fallos, lo que resulta útil cuando se modelan sistemas con períodos de rodaje o componentes con períodos de garantía en los que es imposible que se produzcan fallos prematuros.

Los diferentes campos utilizan diferentes notaciones, por lo que es posible que veas (k,λ) en ingeniería de fiabilidad o (β,η) en análisis de supervivencia. Las relaciones matemáticas siguen siendo las mismas independientemente de la notación que encuentres.

Caracterización matemática y propiedades estadísticas

La base matemática de la distribución de Weibull proporciona las herramientas necesarias para aplicaciones prácticas. Exploremos las funciones principales que hacen que esta distribución sea útil.

Funciones y métricas principales

La función de densidad de probabilidad (PDF) describe la probabilidad de que se produzca un fallo en un momento específico. Para la distribución de Weibull, esto es:

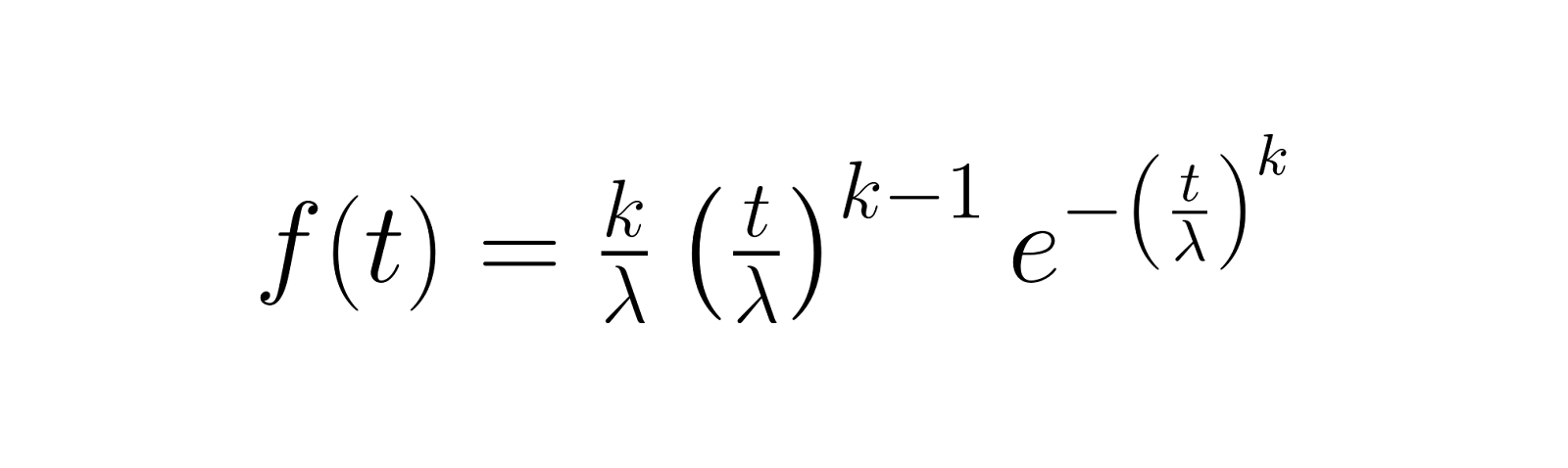
Esta función muestra cómo cambia la densidad de probabilidad de fallo a lo largo del tiempo, siendo el parámetro de forma k el que determina si los fallos son más probables al principio (k < 1), constantes a lo largo del tiempo (k = 1) o si aumentan con el tiempo (k > 1).

La función de distribución acumulativa (CDF) indica la probabilidad de que se produzca un fallo en un momento determinado:

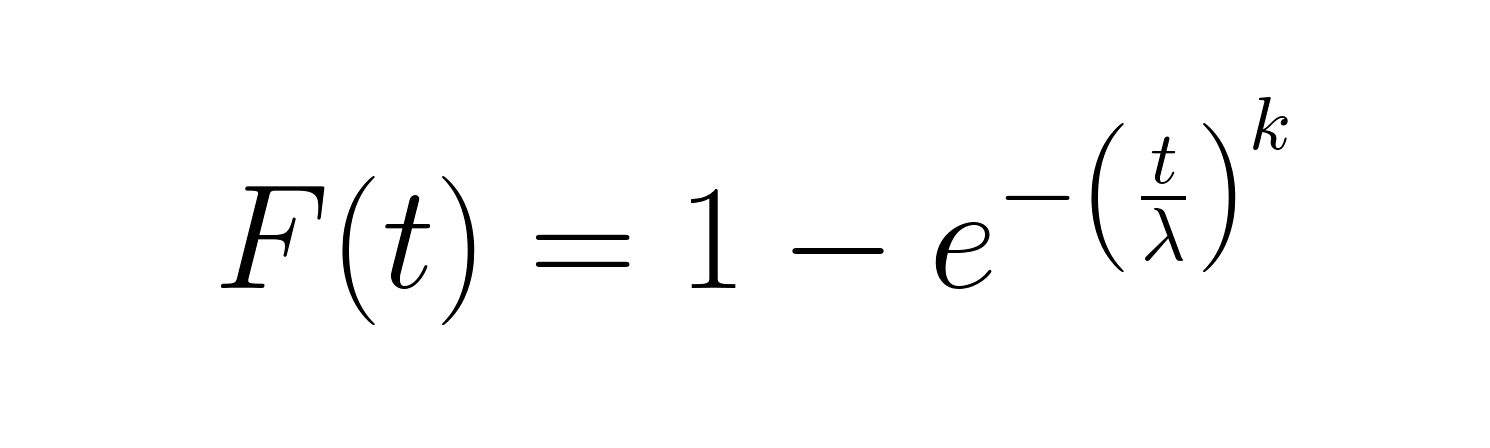
Esta función funciona bien para calcular el porcentaje de elementos que se espera que fallen en un plazo determinado. La función de fiabilidad (1-CDF) proporciona la perspectiva complementaria, mostrando la probabilidad de supervivencia más allá del tiempo t.

La función de riesgo revela la tasa de fallo instantánea en un momento dado:

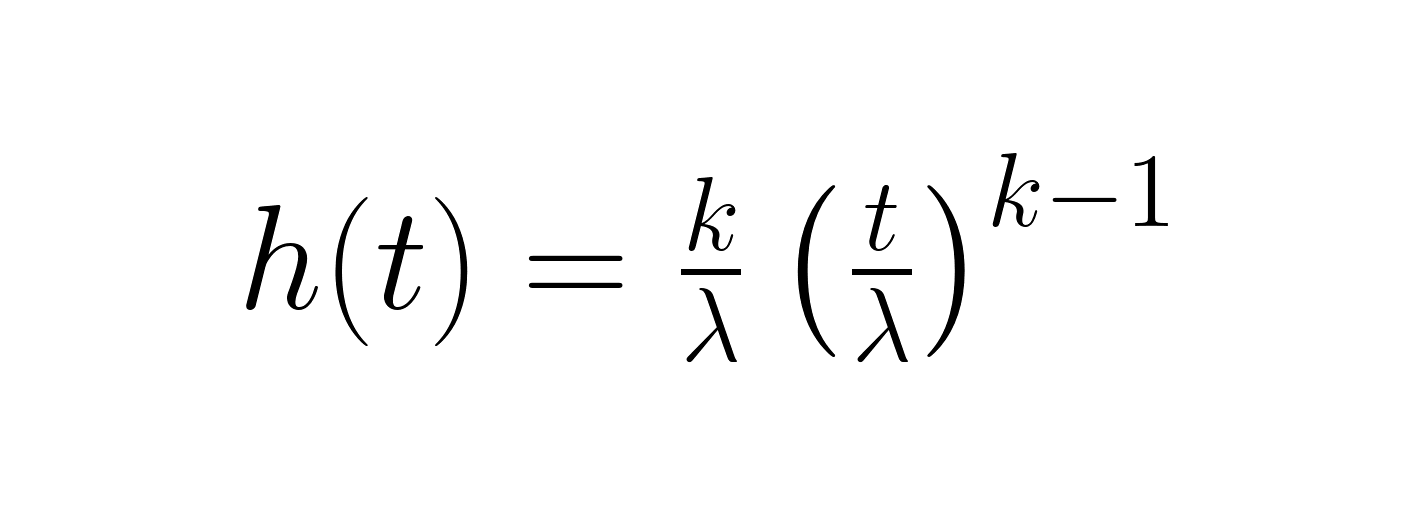
Esta función es esencial para comprender cómo cambia el riesgo a lo largo del tiempo. Cuando k < 1, el riesgo disminuye (mejorando la fiabilidad), cuando k = 1, permanece constante, y cuando k > 1, aumenta (deteriorando la fiabilidad). La función de supervivencia, idéntica a la función de fiabilidad, representa la probabilidad de sobrevivir más allá de un tiempo determinado.

Los momentos estadísticos caracterizan las tendencias centrales y la variabilidad de la distribución. La media implica la función gamma y depende de ambos parámetros, lo que la hace más compleja que la vida característica. La varianza cuantifica la dispersión alrededor de la media, mientras que la mediana suele ofrecer una interpretación más intuitiva que la media en el caso de distribuciones asimétricas. El modo representa el tiempo de fallo más probable, aunque puede que no exista para todas las combinaciones de parámetros.

La función generadora de momentos captura todos los momentos estadísticos en una sola expresión, mientras que la entropía mide la incertidumbre o el contenido informativo de la distribución. Estas propiedades, junto con los patrones de comportamiento de la tasa de fallos, hacen que la distribución de Weibull sea adecuada para modelar diversos fenómenos del mundo real en los que las hipótesis exponenciales simples resultan inadecuadas.

Fiabilidad condicional y percentiles

Los cálculos de fiabilidad condicional responden a preguntas prácticas como «Si este componente ya ha sobrevivido 1000 horas, ¿cuál es la probabilidad de que dure otras 500 horas?». Esto implica calcular la probabilidad de supervivencia durante un período adicional, dada la supervivencia hasta el momento actual. El cálculo utiliza la siguiente relación:

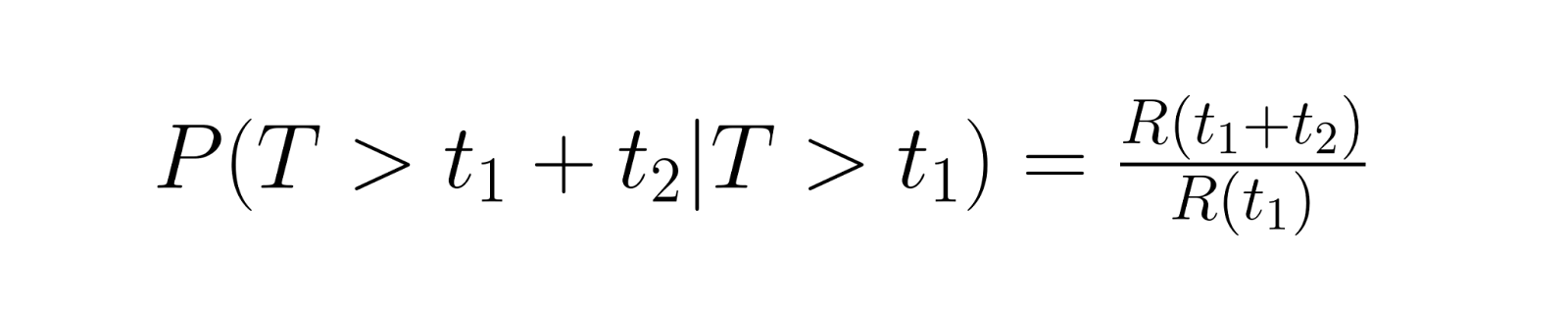
donde R(t) es la función de fiabilidad.

Los percentiles ayudan a estimar métricas importantes a lo largo de la vida útil que impulsan las decisiones empresariales. La vida útil B₁₀ representa el tiempo en el que el 10 % de los artículos habrán fallado, mientras que la vida útil B₉₀ indica cuándo el 90 % de los artículos habrán fallado. Estos percentiles son esenciales para el análisis de la garantía, la planificación del mantenimiento y la evaluación de riesgos.

La función de punto porcentual (CDF inversa) proporciona una estimación cuantílica directa resolviendo F(t) = p para cualquier probabilidad p deseada. Esta función transforma las probabilidades acumulativas de nuevo en valores temporales, lo que te permite determinar tiempos de fallo específicos para niveles de fiabilidad determinados. La mayoría de los paquetes de software estadístico incluyen funciones integradas para estos cálculos, lo que facilita la estimación de percentiles una vez que se han estimado los parámetros de Weibull.

Metodologías de estimación de parámetros

Entender las propiedades matemáticas es una cosa, pero ¿cómo se determinan realmente estos parámetros a partir de los datos? Para estimar los parámetros de Weibull a partir de los datos, es necesario elegir el método adecuado para tu situación y las características de los datos. Cada enfoque tiene ventajas y limitaciones distintas.

Estimación de máxima verosimilitud (MLE)

El MLE proporciona el enfoque más riguroso desde el punto de vista estadístico para la estimación de parámetros. Encuentra los valores de los parámetros que maximizan la probabilidad de observar tus datos reales, lo que lo hace eficaz con conjuntos de datos completos. Piensa en ello como en encontrar los parámetros que hacen que los datos observados sean «más probables» de haber ocurrido.

El método maneja datos censurados (cuando se sabe que los elementos sobrevivieron hasta un cierto punto, pero no se conoce el momento exacto en que fallaron) mediante algoritmos especializados. Esto resulta útil en las pruebas de fiabilidad, en las que no siempre puedes esperar a que todos los elementos fallen. ​La mayoría de los paquetes de software estadístico incluyen rutinas MLE diseñadas específicamente para el análisis de Weibull. Aunque la complejidad computacional aumenta con el tamaño del conjunto de datos, las implementaciones modernas manejan de manera eficiente conjuntos de datos con cientos de miles de observaciones.

Método de los momentos (MOM)

El enfoque MOM estima los parámetros comparando los momentos teóricos con los momentos muestrales de tus datos. Aunque es menos eficiente estadísticamente que el MLE, ofrece simplicidad computacional y, a menudo, proporciona buenas estimaciones iniciales para métodos más complejos.

Este enfoque funciona bien cuando necesitas estimaciones rápidas o cuando se trata de datos que no se ajustan perfectamente a los supuestos del MLE. También resulta útil para hacerse una idea aproximada de los parámetros antes de sumergirse en análisis más sofisticados.

Mínimos cuadrados y técnicas gráficas

Los gráficos de probabilidad de Weibull transforman los datos en coordenadas logarítmicas, donde las distribuciones de Weibull aparecen como líneas rectas, lo que te permite validar visualmente el ajuste del modelo mientras estimas los parámetros mediante regresión lineal. El método utiliza papel milimetrado a escala especial (ahora reproducido digitalmente en software) con una transformación logarítmica doble que linealiza la función de distribución acumulativa de Weibull.

El proceso consiste en clasificar los datos de fallos de menor a mayor, calcular las posiciones medias de cada punto de datos (que estiman la probabilidad acumulativa de fallo) y gráficando los tiempos de fallo en función de estas probabilidades. Si tus datos siguen una distribución de Weibull, los puntos formarán aproximadamente una línea recta cuya pendiente es igual al parámetro de forma y cuya posición determina el parámetro de escala. Es un método antiguo, pero funciona y la retroalimentación visual es valiosa para comprender tus datos. Cuando los puntos se desvían significativamente de la linealidad, esto sugiere que el modelo de Weibull puede no ser adecuado para tu conjunto de datos, lo que hace que esta técnica sea valiosa tanto para la estimación de parámetros como para la validación de modelos.

Desafíos de tres parámetros

Estimar el parámetro de ubicación θ presenta dificultades únicas, ya que afecta al límite inferior de la distribución. El MLE estándar puede producir estimaciones poco fiables cuando θ se aproxima al tiempo mínimo de fallo observado.

Los métodos de verosimilitud del perfil abordan estos problemas de estimación tratando θ como un parámetro molesto, lo que proporciona estimaciones más estables para los parámetros de forma y escala. Es un poco más complejo, pero a menudo necesario para obtener resultados fiables.

Aplicaciones en diversas disciplinas

La versatilidad de la distribución de Weibull se pone de manifiesto en sus aplicaciones en diversos campos. Cada dominio aprovecha aspectos específicos de la flexibilidad de la distribución.

Ingeniería de fiabilidad

Los ingenieros de fiabilidad utilizan el análisis de Weibull para realizar pruebas de vida útil aceleradas, en las que los productos se someten a condiciones de estrés para predecir su vida útil en condiciones normales de uso. En lugar de esperar años para ver cuánto dura algo, puedes someterlo a pruebas de estrés y extrapolar los resultados a condiciones normales.

El análisis de la garantía se basa en modelos Weibull para estimar futuras reclamaciones y establecer períodos de cobertura adecuados. Las empresas necesitan saber cuántos productos fallarán dentro de los períodos de garantía para fijar el precio correcto de sus productos.

La programación del mantenimiento preventivo se beneficia de la capacidad de Weibull para modelar las tasas de fallo variables a lo largo del ciclo de vida de los equipos. A diferencia de los modelos exponenciales, que asumen tasas de fallo constantes, Weibull puede indicarte cuándo empiezan a aumentar las tasas de fallo, lo que te ayuda a programar el mantenimiento antes de que se produzcan averías.

Ciencias médicas y biológicas

El análisis de supervivencia en la investigación médica suele emplear modelos de Weibull para estudiar la eficacia de los tratamientos y el pronóstico de los pacientes. La distribución maneja de forma natural los datos censurados habituales en los ensayos clínicos, en los que los pacientes pueden abandonar el estudio antes de experimentar el evento de interés.

La regresión de Weibull amplía el análisis básico al incorporar las características de los pacientes (edad, tipo de tratamiento, estadio de la enfermedad) como covariables. Esto proporciona estimaciones de supervivencia personalizadas que son esenciales para planificar el tratamiento, lo que ayuda a los médicos a ofrecer a los pacientes expectativas realistas sobre su pronóstico.

Ciencia de los materiales y silvicultura

Los ingenieros de materiales utilizan las distribuciones de Weibull para modelar la resistencia de materiales frágiles como la cerámica y los compuestos, en los que el eslabón más débil determina el fallo general. La capacidad de la distribución para modelar valores extremos la hace ideal para estas aplicaciones en las que te preocupa el peor de los casos.

La gestión forestal aplica los modelos de Weibull a la distribución del diámetro de los árboles, lo que ayuda a predecir el rendimiento de las cosechas y a planificar operaciones forestales sostenibles. Es una aplicación práctica que ayuda a equilibrar las preocupaciones económicas y medioambientales.

Energía eólica y estudios medioambientales

Aunque este artículo se centra en aplicaciones relacionadas con el tiempo hasta que se produce un evento, las distribuciones de Weibull también modelan otros fenómenos en ingeniería medioambiental. La evaluación de los recursos eólicos utiliza el modelo de Weibull para caracterizar los patrones de velocidad del viento en los emplazamientos potenciales para turbinas, donde los parámetros de forma indican la consistencia del viento para la planificación de la producción de energía.

Temas avanzados y extensiones

Por muy útiles que sean estas aplicaciones estándar, los problemas actuales a menudo requieren ir más allá del análisis básico de Weibull. 

Selección de modelos y bondad de ajuste

Elegir entre la distribución de Weibull y otras distribuciones alternativas requiere realizar pruebas sistemáticas utilizando estadísticas de bondad de ajuste, como las pruebas de Kolmogorov-Smirnov y Anderson-Darling. Estas pruebas cuantifican en qué medida la distribución elegida se ajusta a los patrones de datos observados, lo que te da confianza en la elección de tu modelo.

Los diagnósticos gráficos complementan las pruebas estadísticas al revelar patrones que los números por sí solos podrían pasar por alto. El análisis residual ayuda a identificar desviaciones sistemáticas del comportamiento esperado, mientras que los criterios de información (AIC/BIC) equilibran el ajuste del modelo con la complejidad. Básicamente, quieres un modelo que se ajuste bien sin ser innecesariamente complicado.

Modelos de regresión y modelos mixtos

La regresión de Weibull incorpora variables explicativas directamente en los parámetros de distribución, lo que te permite modelar cómo factores como la temperatura, la carga o las características del paciente afectan al comportamiento ante fallos. Esta extensión es útil en pruebas de fiabilidad e investigación médica, donde múltiples factores influyen en los resultados.

Los modelos mixtos de Weibull manejan poblaciones con subgrupos distintos (como diferentes modos de fallo) combinando múltiples distribuciones de Weibull. Piensa en una población en la que algunos artículos fallan por desgaste, mientras que otros fallan por defectos aleatorios. Necesitas diferentes modelos para cada modo de fallo.

Las aplicaciones de machine learning utilizan cada vez más estos modelos para el reconocimiento de patrones complejos y aplicaciones de redes neuronales, tendiendo un puente entre los métodos estadísticos tradicionales y las técnicas modernas de inteligencia artificial.

Riesgos competitivos y modelos de degradación

Algunos sistemas se enfrentarán a múltiples modos de fallo simultáneamente. El desgaste mecánico, los fallos eléctricos y la degradación medioambiental pueden afectar al mismo componente. Los modelos de riesgos competitivos utilizan múltiples distribuciones de Weibull para representar cada modo de fallo, lo que te ayuda a comprender qué riesgos son más críticos.

Los modelos de degradación realizan un seguimiento de cómo disminuye el rendimiento del sistema con el tiempo, utilizando distribuciones de Weibull para modelar el tiempo hasta que el rendimiento cae por debajo de los umbrales aceptables. Esto resulta útil para sistemas en los que se puede medir la degradación antes de que se produzca un fallo completo.

Formularios relacionados y especiales

La distribución inversa de Weibull modela situaciones en las que es menos probable que se den valores más altos, como la resistencia mínima de los materiales o los tiempos de supervivencia más cortos en biología. Esta variante resulta útil cuando las hipótesis tradicionales de Weibull no se ajustan a los patrones de tus datos.

Las distribuciones discretas de Weibull adaptan el modelo continuo a datos discretos, como el número de ciclos hasta el fallo o los intervalos de tiempo discretos en los estudios de supervivencia. No es tan habitual, pero resulta útil cuando los datos se presentan en fragmentos discretos en lugar de mediciones continuas.

Conclusión

La adaptabilidad de la distribución de Weibull la hace muy útil para analizar cuándo ocurren las cosas a lo largo del tiempo. Maneja tasas de riesgo crecientes, decrecientes o estables y funciona bien con datos incompletos. Nuestros cursos Análisis de supervivencia en Python y Análisis de supervivencia en R te permiten practicar conconjuntos de datos y métodos establecidos.

Las futuras líneas de investigación incluyen enfoques bayesianos que incorporen los conocimientos previos de forma más eficaz, híbridos de machine learning que combinen el modelo de Weibull con redes neuronales y aplicaciones de big data que adapten los métodos tradicionales a conjuntos de datos masivos.