Distribution de Weibull : Comment modéliser les données relatives au délai avant événement

Lorsque vous analysez la durée de vie des éléments (qu'il s'agisse de la durée de vie des composants électroniques, de la survie des patients ou de la fiabilité des équipements), vous avez besoin d'une distribution capable de gérer la complexité des modèles de défaillance. La distribution de Weibull ne suppose pas que les défaillances se produisent à un rythme constant, contrairement aux modèles plus simples. Au lieu de cela, il peut modéliser des scénarios dans lesquels les taux de défaillance augmentent avec le temps (comme les processus d'usure), diminuent initialement (comme les défauts de fabrication éliminés dès le début) ou restent stables.

Si les concepts de probabilité sont nouveaux pour vous, notre cours « Fondements de la probabilité dans R » couvreles bases statistiques dont vous aurez besoin pour effectuer des travaux avancés sur les distributions. Ce tutoriel vous guidera à travers les fondements mathématiques de la distribution de Weibull. Vous apprendrez à estimer ses paramètres à partir de données et découvrirez comment sa flexibilité le rend particulièrement utile dans l'analyse de fiabilité et les études de survie. À la fin, vous comprendrez non seulement la théorie qui sous-tend cette distribution utile, mais également quand et comment l'appliquer à vos propres défis en matière d'analyse du temps jusqu'à l'événement.

Qu'est-ce que la distribution de Weibull ?

La distribution de Weibull est une distribution de probabilité continue conçue pour modéliser les données relatives au temps écoulé jusqu'à un événement. Vous le rencontrerez le plus souvent dans l'analyse des défaillances, les études de survie et l'ingénierie de fiabilité, où l'objectif est de comprendre « quand quelque chose se produit ». 

Ce qui distingue la loi de Weibull des alternatives plus simples, c'est sa capacité d'adaptation à différents modèles de défaillance. Alors que certaines distributions supposent que les événements se produisent à un rythme régulier et prévisible, la distribution de Weibull permet de gérer des situations où la probabilité des événements évolue au fil du temps. Cette flexibilité est particulièrement utile lorsque vous travaillez avec des systèmes ou des processus complexes dont les mécanismes sous-jacents ne sont pas entièrement compris.

Contexte historique et principes fondamentaux

L'histoire derrière cette distribution commence avec le mathématicien suédois Waloddi Weibull, qui l'a développée dans les années 1930 alors qu'il étudiait la résistance et la fatigue des matériaux. Ses travaux ont jeté les bases de l'ingénierie moderne de la fiabilité.

La distribution se présente sous deux formes principales qui répondent à différents besoins analytiques. Le modèle Weibull à deux paramètres utilise des paramètres de forme et d'échelle pour modéliser des scénarios dans lesquels les événements peuvent débuter immédiatement. La version à trois paramètres ajoute un paramètre de localisation, créant ainsi un seuil minimal avant que les événements puissent se produire, ce qui est utile pour modéliser des systèmes avec des délais intégrés ou des périodes de « rodage ».

La distribution de Weibull appartient à une famille de distributions apparentées, dont la distribution exponentielle constitue un cas particulier. Ce lien permet d'expliquer pourquoi les modèles d' s exponentiels et de Weibull sont souvent comparés dans le contexte de la fiabilité. La plus grande flexibilité de la distribution de Weibull lui permet de se rapprocher d'autres distributions bien connues dans des conditions paramétriques spécifiques, ce qui contribue à sa large adoption.

Paramètres de la distribution de Weibull

Maintenant que nous avons abordé l'évolution historique et le comportement de base, examinons les paramètres qui confèrent à la distribution de Weibull sa flexibilité. Chaque paramètre fournit des informations spécifiques sur le comportement de vos données.

Le paramètre de forme (k ou β) contrôle le caractère de la distribution et le comportement de la fonction de risque. Lorsque les valeurs sont inférieures à 1, vous observez des schémas de mortalité infantile où les défaillances précoces sont dues à des défauts de fabrication. Lorsque les valeurs sont supérieures à 1, on observe des défaillances dues à l'usure, c'est-à-dire des pannes résultant d'une utilisation régulière au fil du temps.

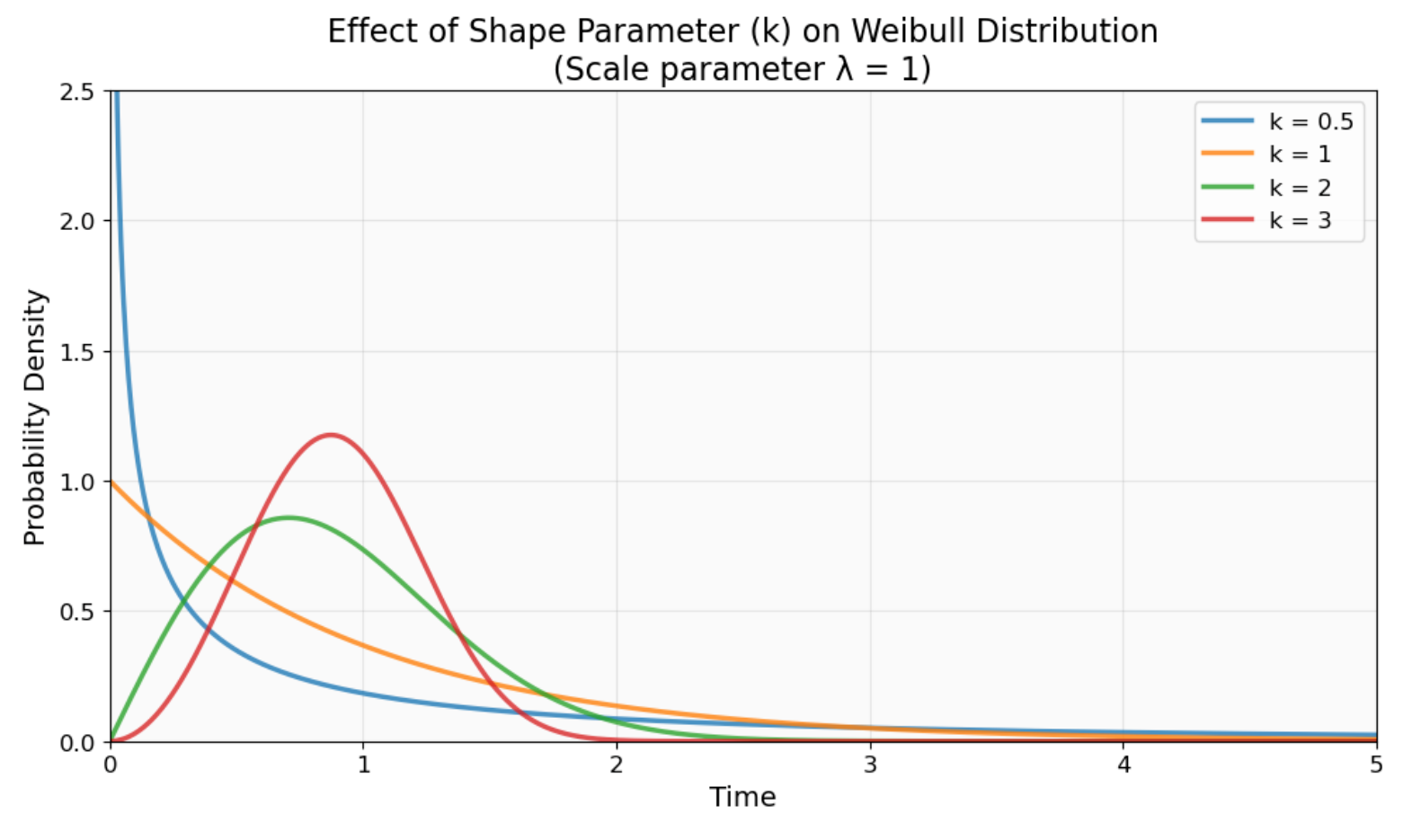
Effet du paramètre de forme (k) sur le comportement de la distribution de Weibull. Veuillez noter comment k < 1 génère une probabilité de défaillance précoce élevée (courbe bleue), k = 1 produit des taux de défaillance constants (orange) et k > 1 montre des taux de défaillance croissants au fil du temps (courbes verte et rouge). Image fournie par l'auteur.

Le paramètre d'échelle (λ ou η) représente la durée de vie caractéristique. Il s'agit du moment où exactement 63,2 % des éléments auront échoué, quelle que soit la valeur du paramètre de forme. Vous pouvez considérer cela comme la durée de vie typique de la distribution, bien que la moyenne réelle puisse différer en raison de la forme de la distribution.

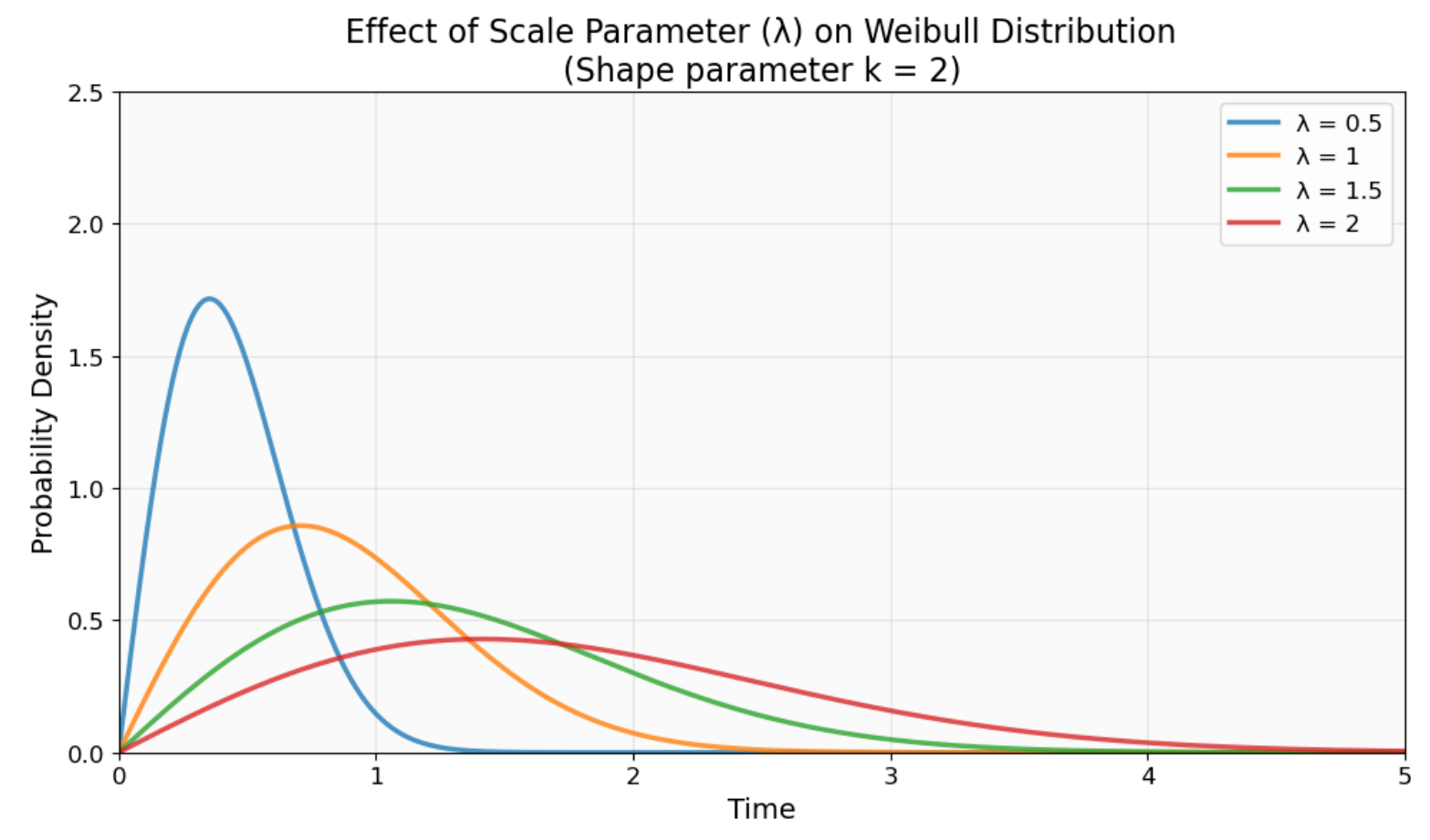
Comment le paramètre d'échelle (λ) modifie la distribution de Weibull le long de l'axe temporel. Des valeurs λ plus élevées étendent la distribution vers la droite (durée de vie caractéristique plus longue), tandis que des valeurs plus faibles la compriment vers la gauche (durée de vie caractéristique plus courte). La forme reste constante. Image fournie par l'auteur.

Dans les applications à trois paramètres, le paramètre de localisation (θ ou γ) déplace la distribution le long de l'axe temporel. Il représente une durée de vie minimale garantie avant que des défaillances ne puissent survenir, ce qui est utile lorsque vous modélisez des systèmes avec des périodes de rodage ou des composants avec des périodes de garantie pendant lesquelles une défaillance précoce est impossible.

Différents domaines utilisent différentes notations, vous pouvez donc voir (k,λ) en ingénierie de fiabilité ou (β,η) en analyse de survie. Les relations mathématiques restent identiques quelle que soit la notation utilisée.

Caractérisation mathématique et propriétés statistiques

Les fondements mathématiques de la distribution de Weibull fournissent les outils nécessaires à des applications pratiques. Explorons les fonctions essentielles qui rendent cette distribution utile.

Fonctions et indicateurs clés

La fonction de densité de probabilité (PDF) décrit la probabilité qu'une défaillance se produise à un moment donné. Pour la distribution de Weibull, cela donne :

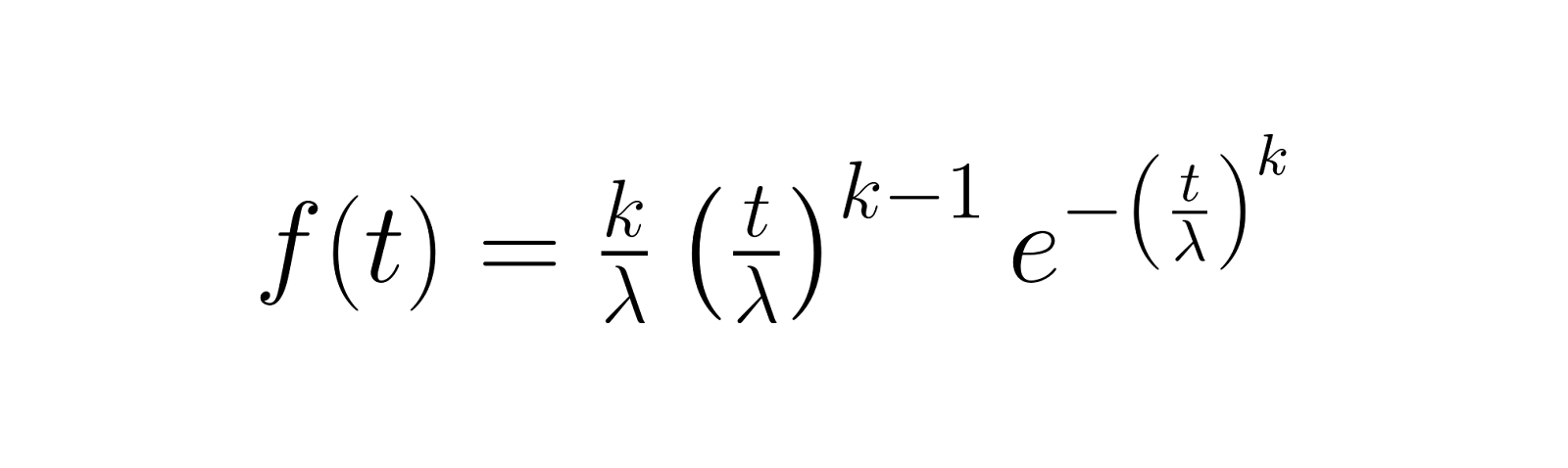
Cette fonction montre comment la densité de probabilité de défaillance évolue au fil du temps, le paramètre de forme k déterminant si les défaillances sont plus susceptibles de se produire tôt (k < 1), si elles restent constantes au fil du temps (k = 1) ou si elles augmentent avec l'âge (k > 1).

La fonction de distribution cumulative (FDC) indique la probabilité qu'une défaillance se produise à un moment donné :

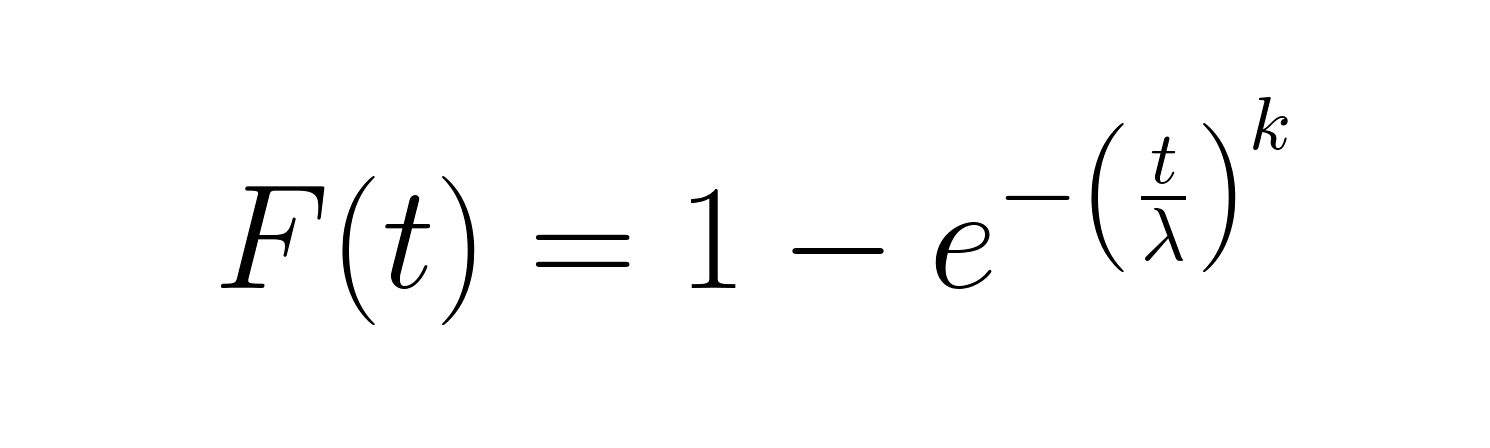
Cette fonction est particulièrement utile pour calculer le pourcentage d'éléments susceptibles de présenter une défaillance au cours d'une période donnée. La fonction de fiabilité (1-CDF) offre une perspective complémentaire, indiquant la probabilité de survie au-delà du temps t.

La fonction de risque indique le taux de défaillance instantané à un moment donné :

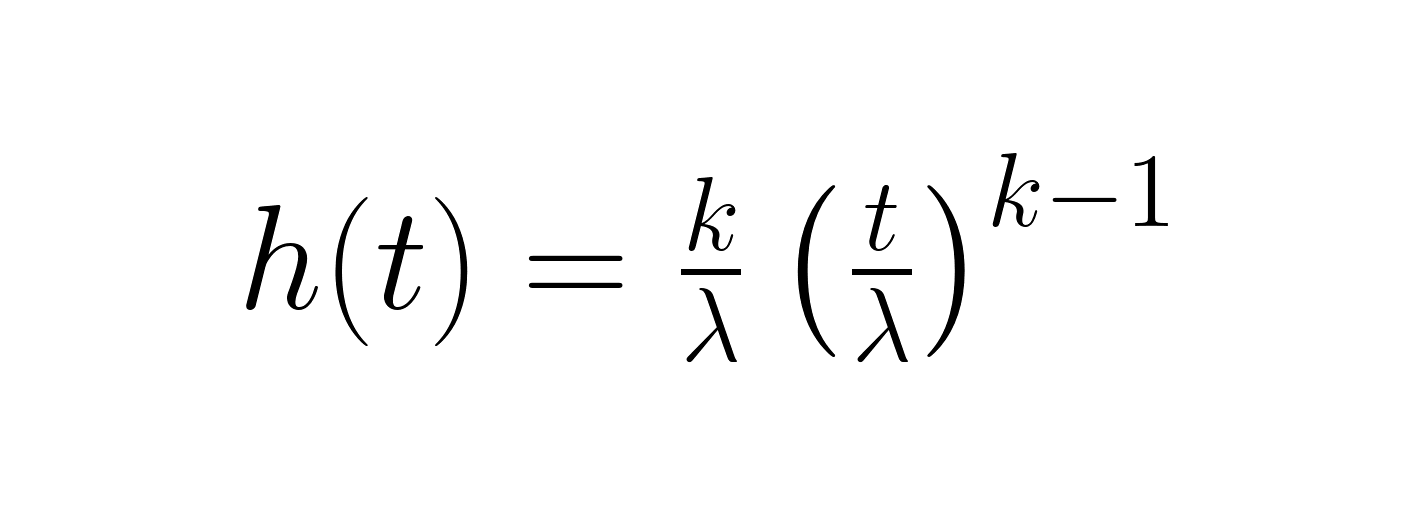
Cette fonction est essentielle pour appréhender l'évolution du risque au fil du temps. Lorsque k < 1, le risque diminue (amélioration de la fiabilité), lorsque k = 1, il reste constant, et lorsque k > 1, il augmente (détérioration de la fiabilité). La fonction de survie, identique à la fonction de fiabilité, représente la probabilité de survie au-delà d'un moment donné.

Les moments statistiques caractérisent les tendances centrales et la variabilité de la distribution. La moyenne implique la fonction gamma et dépend des deux paramètres, ce qui la rend plus complexe que la durée de vie caractéristique. La variance quantifie la dispersion autour de la moyenne, tandis que la médiane fournit souvent une interprétation plus intuitive que la moyenne pour les distributions asymétriques. Le mode représente le moment de défaillance le plus probable, bien qu'il puisse ne pas exister pour toutes les combinaisons de paramètres.

La fonction génératrice des moments capture tous les moments statistiques dans une seule expression, tandis que l'entropie mesure l'incertitude ou le contenu informatif de la distribution. Ces propriétés, associées aux modèles de comportement des taux de défaillance, rendent la distribution de Weibull appropriée pour modéliser divers phénomènes du monde réel où les hypothèses exponentielles simples s'avèrent inadéquates.

Fiabilité conditionnelle et centiles

Les calculs de fiabilité conditionnelle répondent à des questions pratiques telles que « Si ce composant a déjà fonctionné pendant 1 000 heures, quelle est la probabilité qu'il fonctionne encore pendant 500 heures ? » Cela implique de calculer la probabilité de survie pour une période supplémentaire, compte tenu de la survie jusqu'au moment présent. Le calcul utilise la relation suivante :

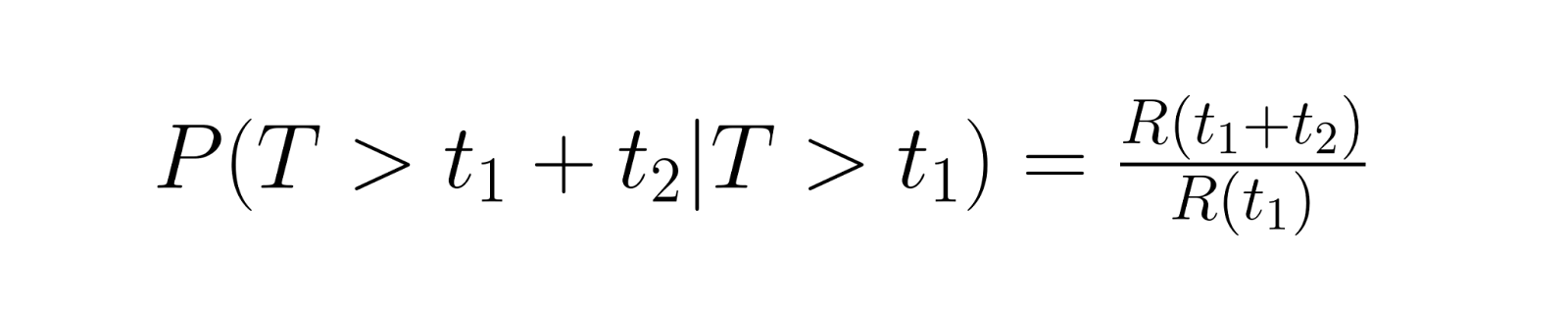
où R(t) est la fonction de fiabilité.

Les centiles permettent d'estimer des indicateurs importants sur toute une vie qui influencent les décisions commerciales. La durée de vie B₁₀ représente le moment où 10 % des articles seront défectueux, tandis que la durée de vie B₉₀ indique le moment où 90 % des articles seront défectueux. Ces percentiles sont essentiels pour l'analyse des garanties, la planification de la maintenance et l'évaluation des risques.

La fonction du point de pourcentage (CDF inverse) fournit une estimation directe des quantiles en résolvant F(t) = p pour toute probabilité p souhaitée. Cette fonction transforme les probabilités cumulées en valeurs temporelles, vous permettant ainsi de déterminer des temps de défaillance spécifiques pour des niveaux de fiabilité donnés. La plupart des logiciels statistiques intègrent des fonctions permettant d'effectuer ces calculs, ce qui facilite l'estimation des centiles une fois que vous avez estimé les paramètres de Weibull.

Méthodes d'estimation des paramètres

Comprendre les propriétés mathématiques est une chose, mais comment déterminez-vous concrètement ces paramètres à partir de vos données ? Pour estimer les paramètres de Weibull à partir de données, il est nécessaire de sélectionner la méthode la plus appropriée à votre situation et aux caractéristiques de vos données. Chaque approche présente des avantages et des limites distincts.

Estimation du maximum de vraisemblance (EMV)

La MLE offre l'approche la plus rigoureuse sur le plan statistique pour l'estimation des paramètres. Il identifie les valeurs des paramètres qui maximisent la probabilité d'observer vos données réelles, ce qui le rend efficace avec des ensembles de données complets. Considérez cela comme la recherche des paramètres qui rendent vos données observées « les plus susceptibles » de s'être produites.

La méthode traite les données censurées (lorsque vous savez que les éléments ont survécu jusqu'à un certain point, mais que vous ne connaissez pas leur date exacte de défaillance) à l'aide d'algorithmes spécialisés. Ceci est utile dans les tests de fiabilité où il n'est pas toujours possible d'attendre que chaque élément tombe en panne. ​La plupart des logiciels statistiques comprennent des routines MLE spécialement conçues pour l'analyse de Weibull. Bien que la complexité informatique augmente avec la taille des ensembles de données, les implémentations modernes traitent efficacement des ensembles de données contenant des centaines de milliers d'observations.

Méthode des moments (MOM)

L'approche MOM estime les paramètres en faisant correspondre les moments théoriques aux moments échantillonnés à partir de vos données. Bien que moins efficace statistiquement que le MLE, il offre une simplicité de calcul et fournit souvent de bonnes estimations de départ pour des méthodes plus complexes.

Cette approche est efficace lorsque vous avez besoin d'estimations rapides ou lorsque vous traitez des données qui ne correspondent pas parfaitement aux hypothèses du MLE. Cela est également utile pour obtenir une idée approximative de vos paramètres avant de vous lancer dans une analyse plus approfondie.

Méthodes des moindres carrés et techniques graphiques

Les graphiques de probabilité de Weibull transforment les données en coordonnées logarithmiques où les distributions de Weibull apparaissent sous forme de lignes droites, ce qui vous permet de valider visuellement l'ajustement du modèle tout en estimant les paramètres par régression linéaire. Cette méthode utilise du papier millimétré spécialement calibré (aujourd'hui reproduit numériquement dans un logiciel) avec une transformation double logarithmique qui linéarise la fonction de distribution cumulative de Weibull.

Le processus consiste à classer vos données de défaillance de la plus petite à la plus grande, à calculer les positions médianes pour chaque point de données (qui estiment la probabilité cumulative de défaillance) et à réaliser un graphique des temps de défaillance par rapport à ces probabilités. Si vos données suivent une distribution de Weibull, les points formeront approximativement une ligne droite dont la pente est égale au paramètre de forme et dont la position détermine le paramètre d'échelle. C'est une méthode traditionnelle, mais elle est efficace et le retour visuel est précieux pour comprendre vos données. Lorsque les points s'écartent considérablement de la linéarité, cela suggère que le modèle de Weibull pourrait ne pas convenir à votre ensemble de données, ce qui rend cette technique utile tant pour l'estimation des paramètres que pour la validation du modèle.

Défis à trois paramètres

L'estimation du paramètre de localisation θ présente des difficultés particulières, car il affecte la limite inférieure de la distribution. La MLE standard peut produire des estimations peu fiables lorsque θ s'approche du temps de défaillance minimum observé.

Les méthodes de vraisemblance du profil résolvent ces problèmes d'estimation en traitant θ comme un paramètre perturbateur, ce qui permet d'obtenir des estimations plus stables pour les paramètres de forme et d'échelle. C'est un peu plus complexe, mais souvent nécessaire pour obtenir des résultats fiables.

Applications dans différentes disciplines

La polyvalence de la distribution de Weibull est mise en évidence par ses applications dans divers domaines. Chaque domaine exploite des aspects spécifiques de la flexibilité de la distribution.

Ingénierie de fiabilité

Les ingénieurs en fiabilité utilisent l'analyse de Weibull pour les essais de vieillissement accéléré, au cours desquels les produits sont testés dans des conditions extrêmes afin de prédire leur durée de vie en utilisation normale. Au lieu d'attendre plusieurs années pour déterminer la durée de vie d'un produit, il est possible de le soumettre à des tests de résistance et d'extrapoler les résultats à des conditions normales.

L'analyse des garanties s'appuie sur les modèles de Weibull pour estimer les réclamations futures et définir des périodes de couverture appropriées. Les entreprises doivent connaître le nombre de produits qui présenteront des défaillances pendant la période de garantie afin de fixer correctement le prix de leurs produits.

La planification de la maintenance préventive bénéficie de la capacité de Weibull à modéliser l'évolution des taux de défaillance tout au long du cycle de vie des équipements. Contrairement aux modèles exponentiels qui supposent des taux de défaillance constants, Weibull peut vous indiquer quand les taux de défaillance commencent à augmenter, vous aidant ainsi à planifier la maintenance avant que les équipements ne tombent en panne.

Sciences médicales et biologiques

L'analyse de survie dans la recherche médicale utilise fréquemment les modèles de Weibull pour étudier l'efficacité des traitements et le pronostic des patients. La distribution traite naturellement les données censurées courantes dans les essais cliniques, où les patients peuvent quitter l'étude avant d'avoir connu l'événement d'intérêt.

La régression de Weibull élargit l'analyse de base en intégrant les caractéristiques des patients (âge, type de traitement, stade de la maladie) en tant que covariables. Cela permet d'obtenir des estimations de survie personnalisées, essentielles à la planification du traitement, et aide les médecins à donner aux patients des attentes réalistes quant à leur pronostic.

Science des matériaux et sylviculture

Les ingénieurs en matériaux utilisent les distributions de Weibull pour modéliser la résistance des matériaux fragiles tels que la céramique et les composites, où le maillon le plus faible détermine la défaillance globale. La capacité de la distribution à modéliser des valeurs extrêmes la rend idéale pour ces applications où le scénario le plus défavorable est pris en compte.

La gestion forestière utilise les modèles de Weibull pour analyser la distribution des diamètres des arbres, ce qui permet de prévoir les rendements de récolte et de planifier des opérations forestières durables. Il s'agit d'une application pratique qui contribue à concilier les préoccupations économiques et environnementales.

Énergie éolienne et études environnementales

Bien que cet article se concentre sur les applications liées au temps avant événement, les distributions de Weibull modélisent également d'autres phénomènes en génie environnemental. L'évaluation des ressources éoliennes utilise la loi de Weibull pour caractériser les régimes de vitesse du vent sur les sites potentiels d'implantation d'éoliennes, où les paramètres de forme indiquent la régularité du vent pour la planification de la production d'énergie.

Sujets avancés et extensions

Aussi utiles que soient ces applications standard, les problèmes modernes nécessitent souvent d'aller au-delà de l'analyse Weibull de base. 

Sélection du modèle et qualité de l'ajustement

Le choix entre la distribution de Weibull et d'autres distributions nécessite des tests systématiques à l'aide de statistiques d'adéquation telles que les tests de Kolmogorov-Smirnov et d'Anderson-Darling. Ces tests évaluent dans quelle mesure la distribution que vous avez choisie correspond aux modèles de données observés, vous permettant ainsi d'avoir confiance dans votre choix de modèle.

Les diagnostics graphiques complètent les tests statistiques en révélant des tendances que les chiffres seuls pourraient ne pas mettre en évidence. L'analyse résiduelle permet d'identifier les écarts systématiques par rapport au comportement attendu, tandis que les critères d'information (AIC/BIC) équilibrent l'adéquation du modèle et sa complexité. Vous recherchez essentiellement un modèle qui s'adapte bien sans être inutilement compliqué.

Modèles de régression et modèles mixtes

La régression de Weibull intègre directement les variables explicatives dans les paramètres de distribution, ce qui vous permet de modéliser la manière dont des facteurs tels que la température, la charge ou les caractéristiques des patients influencent le comportement en cas de défaillance. Cette extension est utile dans les tests de fiabilité et la recherche médicale, où de multiples facteurs influencent les résultats.

Les modèles Weibull mixtes traitent les populations comportant des sous-groupes distincts (tels que différents modes de défaillance) en combinant plusieurs distributions Weibull. Considérons une population dans laquelle certains articles tombent en panne à cause de l'usure, tandis que d'autres tombent en panne à cause de défauts aléatoires. Il est nécessaire de disposer de différents modèles pour chaque mode de défaillance.

Les applications d'apprentissage automatique utilisent de plus en plus ces modèles pour la reconnaissance de formes complexes et les applications de réseaux neuronaux, faisant ainsi le pont entre les méthodes statistiques traditionnelles et les techniques modernes d'intelligence artificielle.

Risques concurrents et modèles de dégradation

Certains systèmes peuvent être confrontés à plusieurs modes de défaillance simultanément. L'usure mécanique, les défaillances électriques et la dégradation environnementale peuvent toutes menacer le même composant. Les modèles de risques concurrents utilisent plusieurs distributions de Weibull pour représenter chaque mode de défaillance, ce qui vous aide à identifier les risques les plus critiques.

Les modèles de dégradation suivent la baisse des performances du système au fil du temps, en utilisant les distributions de Weibull pour modéliser le temps nécessaire pour que les performances tombent en dessous des seuils acceptables. Ceci est particulièrement utile pour les systèmes où il est possible de mesurer la dégradation avant qu'une défaillance complète ne se produise.

Formulaires connexes et spéciaux

La distribution inverse de Weibull modélise les situations dans lesquelles les valeurs élevées sont moins susceptibles de se produire, telles que la résistance minimale des matériaux ou les durées de survie les plus courtes en biologie. Cette variante est utile lorsque les hypothèses traditionnelles de Weibull ne correspondent pas à vos modèles de données.

Les distributions de Weibull discrètes adaptent le modèle continu aux données discrètes, telles que le nombre de cycles jusqu'à la défaillance ou les intervalles de temps discrets dans les études de survie. Ce n'est pas très courant, mais cela peut s'avérer utile lorsque vos données se présentent sous forme de blocs distincts plutôt que de mesures continues.

Conclusion

La distribution de Weibull est particulièrement utile pour analyser les événements qui se produisent au fil du temps en raison de sa grande adaptabilité. Il traite les taux de risque croissants, décroissants ou stables et fonctionne efficacement avec des données incomplètes. Nos cours « Analyse de survie en Python » et « Analyse de survie en R » vous permettent de vous exercer à l'aided'ensembles de données et de méthodes établies.

Les orientations futures de la recherche comprennent les approches bayésiennes qui intègrent plus efficacement les connaissances préalables, les hybrides d'apprentissage automatique qui combinent la modélisation de Weibull avec les réseaux neuronaux, et les applications de mégadonnées qui adaptent les méthodes traditionnelles à des ensembles de données massifs.