Distribuição de Weibull: Como modelar dados de tempo até o evento

Quando você está analisando quanto tempo as coisas duram (seja a vida útil de componentes eletrônicos, o tempo de sobrevivência de pacientes ou a confiabilidade de equipamentos), você precisa de uma distribuição que possa lidar com a complexidade dos padrões de falha. A distribuição de Weibull não assume que as falhas acontecem a uma taxa constante, como fazem os modelos mais simples. Em vez disso, ele pode modelar cenários em que as taxas de falha aumentam com o tempo (como processos de desgaste), diminuem inicialmente (como defeitos de fabricação iniciais sendo eliminados) ou permanecem estáveis.

Se você não conhece os conceitos de probabilidade, nosso curso Fundamentos de Probabilidade em R cobreos fundamentos estatísticos que você vai precisar para trabalhos avançados de distribuição. Este tutorial vai te ajudar a entender os fundamentos matemáticos da distribuição de Weibull. Você vai aprender a estimar seus parâmetros a partir dos dados e ver como sua flexibilidade o torna especialmente útil em análises de confiabilidade e estudos de sobrevivência. No final, você vai entender não só a teoria por trás dessa distribuição útil, mas também quando e como aplicá-la aos seus próprios desafios de análise de tempo até o evento.

O que é a distribuição de Weibull?

A distribuição de Weibull é uma distribuição de probabilidade contínua feita para modelar dados de tempo até um evento. Você vai ver isso com frequência em análises de falhas, estudos de sobrevivência e engenharia de confiabilidade, onde entender “quando algo acontece” é o objetivo. 

O que diferencia a Weibull de alternativas mais simples é a sua adaptabilidade a diferentes padrões de falha. Enquanto algumas distribuições acham que os eventos rolam em taxas constantes e previsíveis, a Weibull dá conta de situações em que a chance dos eventos mudar com o tempo. Essa flexibilidade torna-o útil quando você está trabalhando com sistemas ou processos complexos, nos quais os mecanismos subjacentes não são totalmente compreendidos.

Contexto histórico e princípios básicos

A história por trás dessa distribuição começa com o matemático sueco Waloddi Weibull, que a desenvolveu na década de 1930 enquanto estudava resistência e fadiga de materiais. Seu trabalho foi a base da engenharia de confiabilidade moderna.

A distribuição vem em duas formas principais que atendem a diferentes necessidades analíticas. A distribuição Weibull de dois parâmetros usa parâmetros de forma e escala para modelar cenários em que os eventos podem começar imediatamente. A versão de três parâmetros adiciona um parâmetro de localização, criando um limite mínimo antes que os eventos possam ocorrer — útil para modelar sistemas com atrasos embutidos ou períodos de “burn-in”.

A distribuição de Weibull faz parte de uma família de distribuições parecidas, com a distribuição exponencial sendo um caso especial. Essa conexão ajuda a explicar por que você frequentemente vê os modelos de Weibull e exponencial comparados em contextos de confiabilidade. A flexibilidade mais ampla da Weibull permite aproximar outras distribuições conhecidas sob condições específicas de parâmetros, o que contribui para sua ampla adoção.

Parâmetros da Distribuição de Weibull

Agora que já falamos sobre a história e o comportamento básico, vamos ver os parâmetros que dão flexibilidade à distribuição de Weibull. Cada parâmetro te diz algo específico sobre como seus dados se comportam.

O parâmetro de forma (k ou β) controla o caráter da distribuição e como a função de risco se comporta. Quando os valores são menores que 1, você está vendo padrões de mortalidade infantil em que as falhas iniciais acontecem por causa de defeitos de fabricação. Quando os valores são maiores que 1, você vê falhas por desgaste, onde as coisas quebram com o uso regular ao longo do tempo.

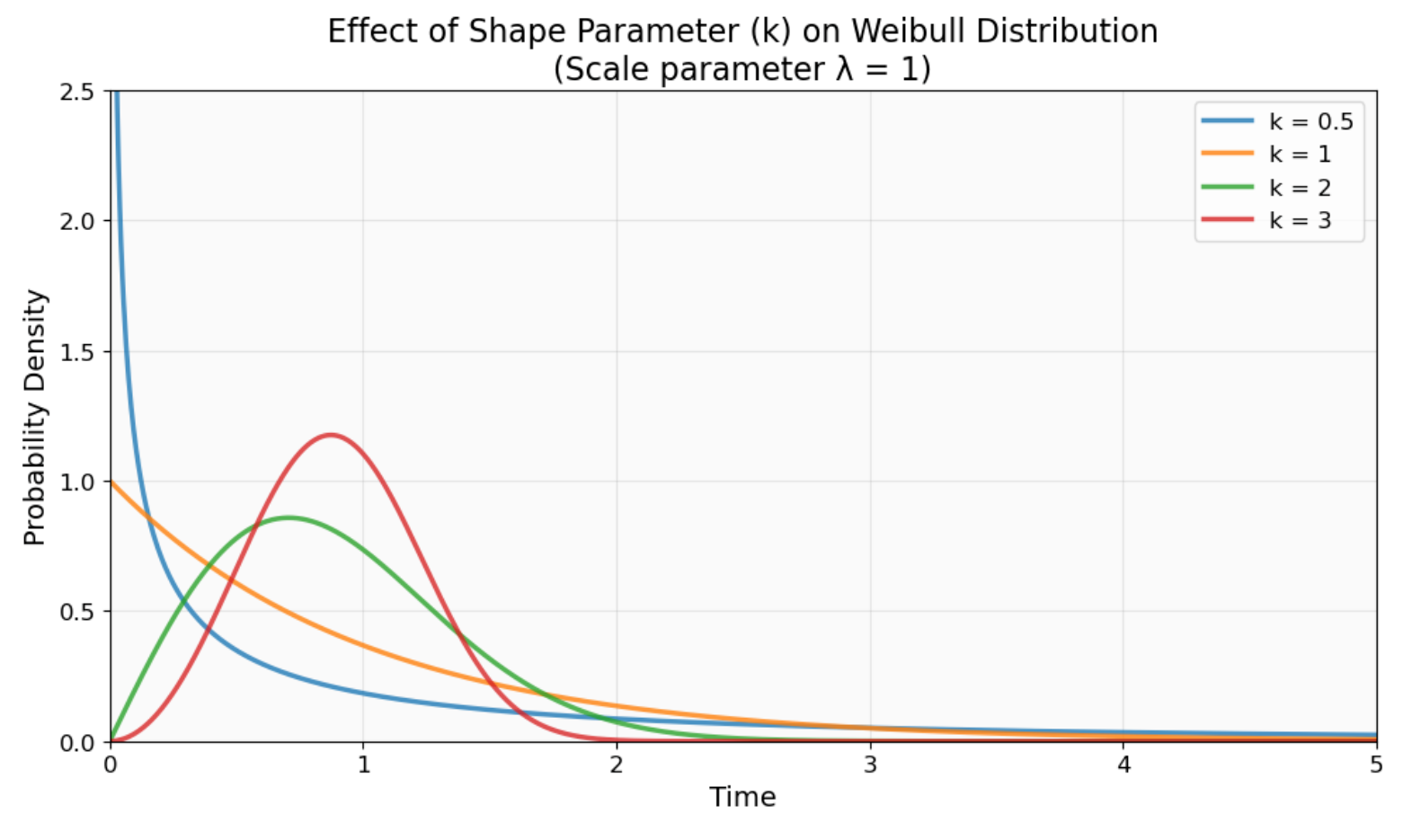
Efeito do parâmetro de forma (k) no comportamento da distribuição de Weibull. Observe como k < 1 cria uma alta probabilidade de falha precoce (curva azul), k = 1 produz taxas de falha constantes (laranja) e k > 1 mostra taxas de falha crescentes ao longo do tempo (curvas verde e vermelha). Imagem do autor.

O parâmetro de escala (λ ou η) mostra a vida útil típica. É o momento em que exatamente 63,2% dos itens vão ter falhado, não importa o valor do parâmetro de forma. Você pode ver isso como a vida útil típica da distribuição, embora a média real possa ser diferente por causa do formato da distribuição.

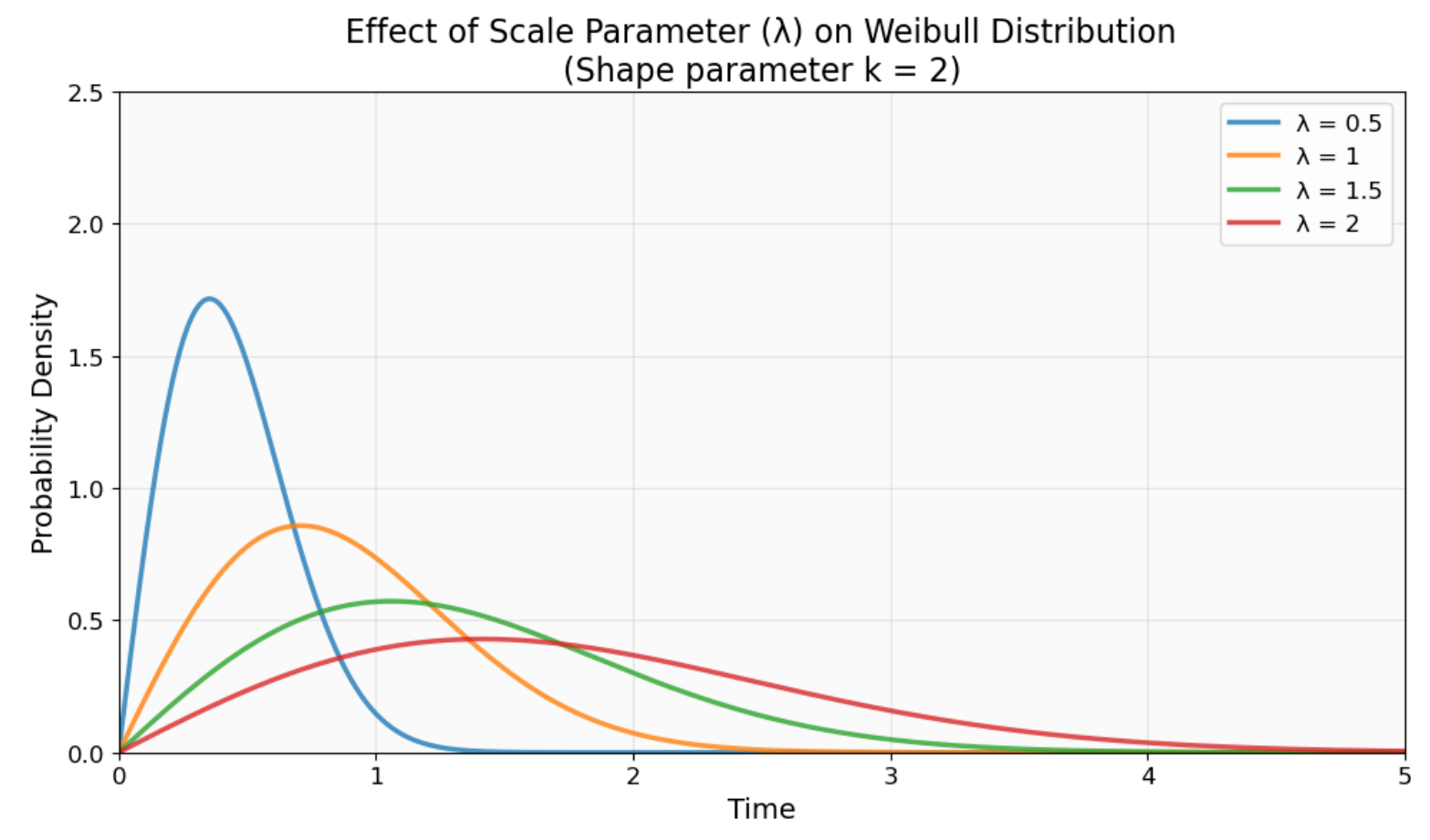
Como o parâmetro de escala (λ) altera a distribuição de Weibull ao longo do eixo temporal. Valores maiores de λ esticam a distribuição para a direita (vida útil mais longa), enquanto valores menores a comprimem para a esquerda (vida útil mais curta). A forma continua igual. Imagem do autor.

Em aplicações de três parâmetros, o parâmetro de localização (θ ou γ) muda a distribuição ao longo do eixo do tempo. Isso mostra um tempo mínimo garantido de vida útil antes que qualquer falha possa começar, o que ajuda quando você está modelando sistemas com períodos de burn-in ou componentes com períodos de garantia em que falhas precoces são impossíveis.

Diferentes áreas usam diferentes notações, então você pode ver (k,λ) em engenharia de confiabilidade ou (β,η) em análise de sobrevivência. As relações matemáticas continuam as mesmas, não importa qual notação você use.

Caracterização matemática e propriedades estatísticas

A base matemática da distribuição de Weibull dá as ferramentas necessárias para aplicações práticas. Vamos ver as principais funções que fazem essa distribuição ser útil.

Funções e métricas principais

A função de densidade de probabilidade (PDF) mostra a chance de algo dar errado em um momento específico. Para a distribuição de Weibull, isso é:

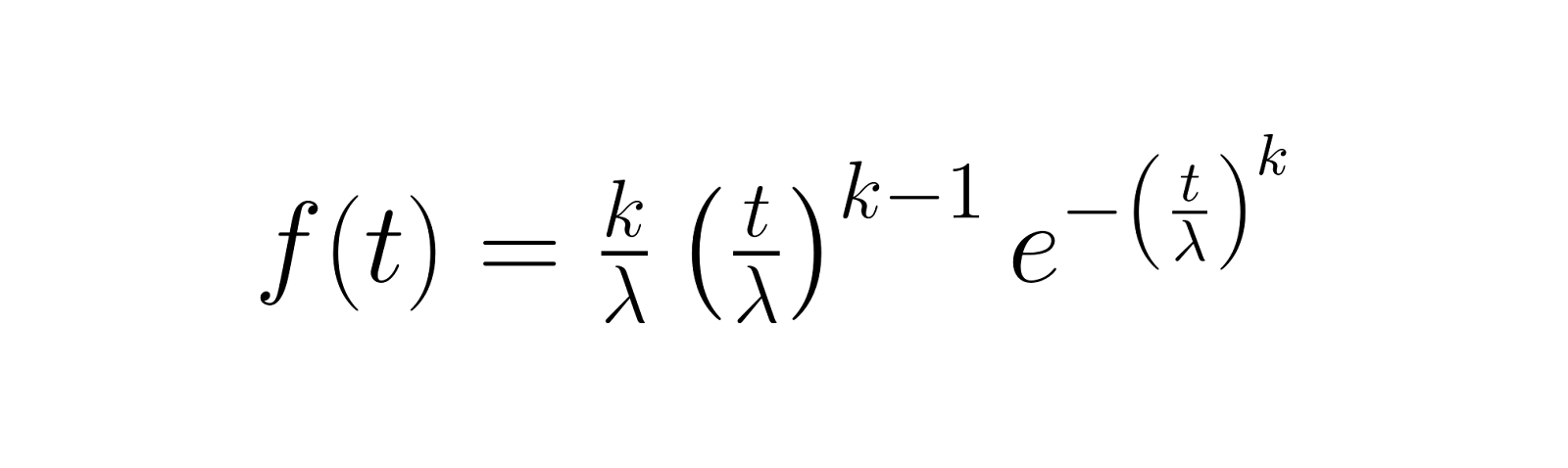
Essa função mostra como a densidade de probabilidade de falha muda com o tempo, com o parâmetro de forma k decidindo se as falhas são mais prováveis no início (k < 1), constantes ao longo do tempo (k = 1) ou aumentando com o tempo (k > 1).

A função de distribuição cumulativa (CDF) mostra a probabilidade de uma falha acontecer até um certo tempo:

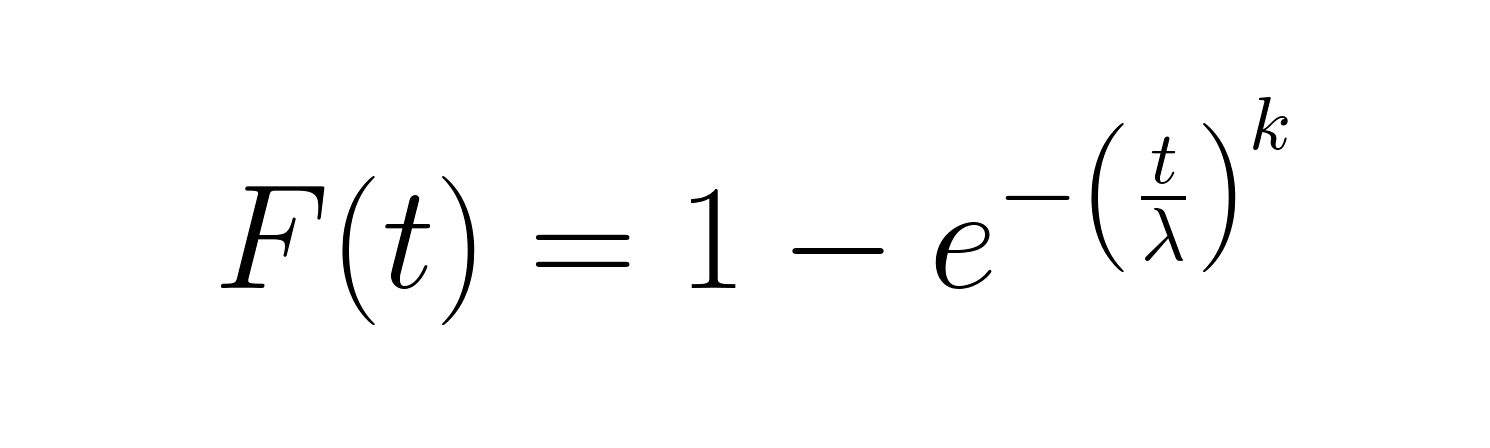
Essa função funciona bem para calcular a porcentagem de itens que devem falhar dentro de um determinado período. A função de confiabilidade (1-CDF) dá uma visão complementar, mostrando a chance de sobreviver além do tempo t.

A função de risco mostra a taxa de falha instantânea em qualquer momento:

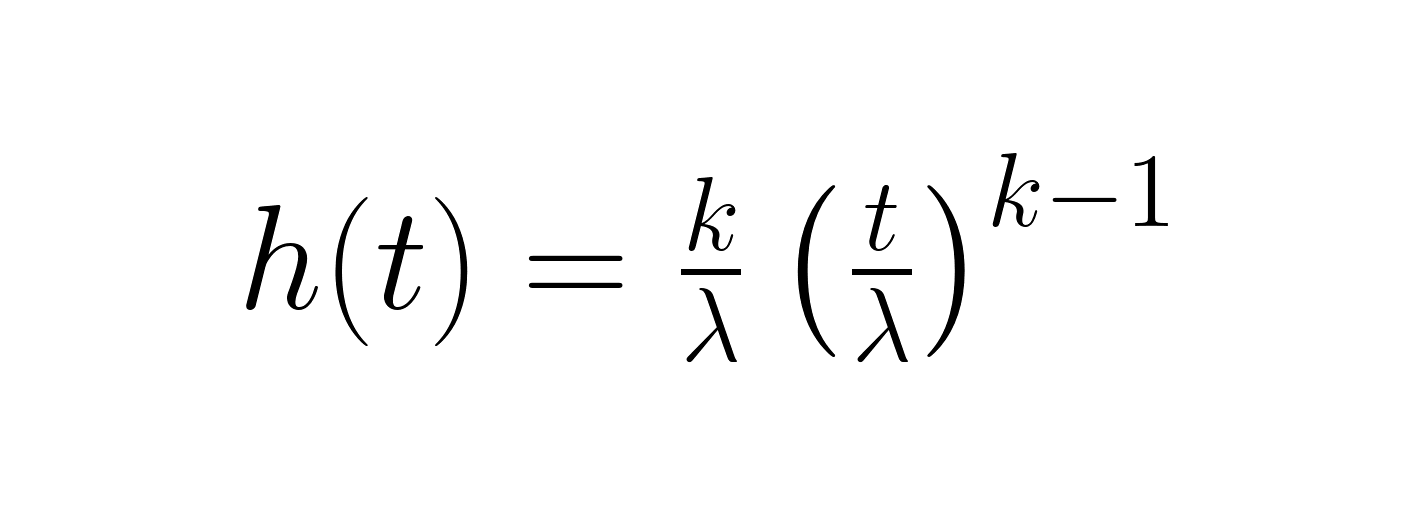
Essa função é essencial para entender como o risco muda com o tempo. Quando k < 1, o risco diminui (melhorando a confiabilidade), quando k = 1, ele fica constante e quando k > 1, ele aumenta (piorando a confiabilidade). A função de sobrevivência, igual à função de confiabilidade, mostra a chance de continuar vivo depois de um certo tempo.

Os momentos estatísticos mostram como a distribuição se comporta em termos de tendências centrais e variabilidade. A média envolve a função gama e depende dos dois parâmetros, o que a torna mais complexa do que a vida característica. A variância mostra como os dados se espalham em torno da média, enquanto a mediana costuma dar uma interpretação mais intuitiva do que a média para distribuições assimétricas. O modo representa o tempo de falha mais provável, embora possa não existir para todas as combinações de parâmetros.

A função geradora de momentos mostra todos os momentos estatísticos numa única expressão, enquanto a entropia mede a incerteza ou o conteúdo informativo da distribuição. Essas propriedades, junto com os padrões de comportamento da taxa de falhas, fazem com que a distribuição de Weibull seja boa para modelar vários fenômenos do mundo real, onde suposições exponenciais simples não dão conta do recado.

Confiabilidade condicional e percentis

Os cálculos de confiabilidade condicional respondem a perguntas práticas como “Se esse componente já durou 1000 horas, qual é a chance de durar mais 500 horas?” Isso envolve calcular a probabilidade de sobrevivência por um período adicional, dada a sobrevivência até o momento atual. O cálculo usa a seguinte relação:

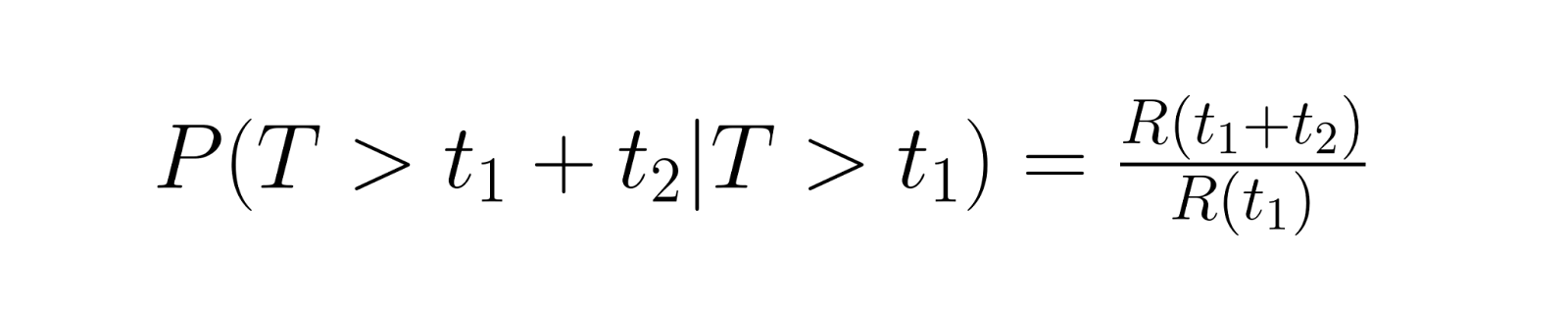
onde R(t) é a função de confiabilidade.

Os percentis ajudam a estimar métricas importantes ao longo da vida que orientam as decisões comerciais. A vida útil B₁₀ é quando 10% dos itens vão dar problema, enquanto a vida útil B₉₀ é quando 90% dos itens vão dar problema. Esses percentis são essenciais para a análise de garantias, planejamento de manutenção e avaliação de riscos.

A função de ponto percentual (CDF inversa) dá uma estimativa direta do quantil resolvendo F(t) = p para qualquer probabilidade p que você quiser. Essa função transforma probabilidades cumulativas de volta em valores de tempo, permitindo que você determine tempos de falha específicos para determinados níveis de confiabilidade. A maioria dos pacotes de software estatístico inclui funções integradas para esses cálculos, tornando a estimativa percentual simples depois que você estima os parâmetros de Weibull.

Métodos de estimativa de parâmetros

Entender as propriedades matemáticas é uma coisa, mas como você realmente determina esses parâmetros a partir dos seus dados? Para estimar os parâmetros de Weibull a partir dos dados, é preciso escolher o método certo para a sua situação e as características dos dados. Cada abordagem tem suas próprias vantagens e limitações.

Estimativa de máxima verossimilhança (MLE)

A MLE oferece a abordagem estatisticamente mais rigorosa para estimativa de parâmetros. Ele encontra valores de parâmetros que maximizam a probabilidade de observar seus dados reais, tornando-o eficaz com conjuntos de dados completos. Pense nisso como encontrar os parâmetros que tornam os dados observados “mais prováveis” de terem ocorrido.

O método lida com dados censurados (onde você sabe que os itens sobreviveram até um certo ponto, mas não sabe exatamente quando falharam) por meio de algoritmos especializados. Isso é útil em testes de confiabilidade, onde nem sempre dá para esperar que todos os itens apresentem falhas. ​A maioria dos pacotes de software estatístico inclui rotinas MLE feitas especialmente para a análise de Weibull. Embora a complexidade computacional aumente com o tamanho do conjunto de dados, as implementações modernas lidam com conjuntos de dados com centenas de milhares de observações de forma eficiente.

Método dos momentos (MOM)

A abordagem MOM estima os parâmetros comparando momentos teóricos com momentos amostrais dos seus dados. Embora seja menos eficiente estatisticamente do que o MLE, oferece simplicidade computacional e, muitas vezes, fornece boas estimativas iniciais para métodos mais complexos.

Essa abordagem funciona bem quando você precisa de estimativas rápidas ou quando lida com dados que não se encaixam perfeitamente nas suposições da MLE. Também é útil para ter uma ideia geral dos seus parâmetros antes de mergulhar em análises mais sofisticadas.

Mínimos quadrados e técnicas gráficas

Os gráficos de probabilidade de Weibull transformam os dados em coordenadas logarítmicas, onde as distribuições de Weibull aparecem como linhas retas, permitindo que você valide visualmente o ajuste do modelo enquanto estima os parâmetros por meio da regressão linear. O método usa papel milimetrado especialmente dimensionado (agora reproduzido digitalmente em software) com uma transformação logarítmica dupla que lineariza a função de distribuição cumulativa de Weibull.

O processo envolve classificar seus dados de falhas do menor para o maior, calcular as posições medianas de classificação para cada ponto de dados (que estimam a probabilidade cumulativa de falha) e plotar os tempos de falha em relação a essas probabilidades. Se seus dados seguirem uma distribuição de Weibull, os pontos formarão aproximadamente uma linha reta cuja inclinação é igual ao parâmetro de forma e cuja posição determina o parâmetro de escala. É um pouco antiquado, mas funciona e o feedback visual é valioso para entender seus dados. Quando os pontos se desviam significativamente da linearidade, isso sugere que o modelo Weibull pode não ser adequado para o seu conjunto de dados, tornando essa técnica valiosa tanto para a estimativa de parâmetros quanto para a validação do modelo.

Desafios de três parâmetros

Estimar o parâmetro de localização θ tem umas dificuldades específicas porque afeta o limite inferior da distribuição. O MLE padrão pode gerar estimativas pouco confiáveis quando θ se aproxima do tempo mínimo de falha observado.

Os métodos de verossimilhança do perfil resolvem esses problemas de estimativa tratando θ como um parâmetro indesejável, o que dá estimativas mais estáveis para os parâmetros de forma e escala. É um pouco mais complicado, mas muitas vezes é necessário para ter resultados confiáveis.

Aplicações em várias áreas

A versatilidade da distribuição de Weibull aparece em suas aplicações em vários campos. Cada domínio aproveita aspectos específicos da flexibilidade da distribuição.

Engenharia de confiabilidade

Os engenheiros de confiabilidade usam a análise de Weibull para testes de vida útil acelerados, onde os produtos são testados em condições de estresse para prever a vida útil em condições normais de uso. Em vez de esperar anos para ver quanto tempo algo dura, você pode fazer um teste de estresse e extrapolar para condições normais.

A análise da garantia usa modelos Weibull para estimar reclamações futuras e definir períodos de cobertura adequados. As empresas precisam saber quantos produtos vão dar problema dentro do prazo de garantia pra definir o preço certo dos produtos.

O planejamento da manutenção preventiva aproveita a capacidade do modelo de Weibull de simular as taxas de falha que mudam ao longo do ciclo de vida dos equipamentos. Diferente dos modelos exponenciais que acham que as taxas de falha são sempre as mesmas, o modelo de Weibull mostra quando essas taxas começam a subir, ajudando você a planejar a manutenção antes que algo dê errado.

Ciências médicas e biológicas

A análise de sobrevivência na pesquisa médica costuma usar modelos Weibull para estudar a eficácia do tratamento e o prognóstico do paciente. A distribuição lida naturalmente com dados censurados, comuns em ensaios clínicos, nos quais os pacientes podem abandonar o estudo antes de experimentar o evento de interesse.

A regressão de Weibull amplia a análise básica ao incluir características dos pacientes (idade, tipo de tratamento, estágio da doença) como covariáveis. Isso dá estimativas personalizadas de sobrevida, que são essenciais para planejar o tratamento, ajudando os médicos a dar aos pacientes expectativas realistas sobre o prognóstico deles.

Ciência dos materiais e silvicultura

Os engenheiros de materiais usam distribuições de Weibull para modelar a resistência de materiais frágeis, como cerâmicas e compósitos, onde o elo mais fraco determina a falha geral. A capacidade da distribuição de modelar valores extremos a torna ideal para essas aplicações em que você se preocupa com o pior cenário possível.

O manejo florestal usa modelos de Weibull para distribuir o diâmetro das árvores, o que ajuda a prever o rendimento da colheita e planejar operações florestais sustentáveis. É uma aplicação prática que ajuda a equilibrar as preocupações econômicas e ambientais.

Energia eólica e estudos ambientais

Embora este artigo se concentre em aplicações de tempo até o evento, as distribuições de Weibull também modelam outros fenômenos na engenharia ambiental. A avaliação dos recursos eólicos usa a distribuição de Weibull para caracterizar os padrões de velocidade do vento em locais potenciais para a instalação de turbinas, onde os parâmetros de forma indicam a consistência do vento para o planejamento da produção de energia.

Tópicos avançados e extensões

Por mais úteis que sejam essas aplicações padrão, os problemas modernos muitas vezes exigem ir além da análise básica de Weibull. 

Seleção do modelo e adequação do ajuste

Escolher entre a distribuição de Weibull e outras distribuições alternativas precisa de testes sistemáticos usando estatísticas de adequação, como os testes de Kolmogorov-Smirnov e Anderson-Darling. Esses testes mostram como a distribuição que você escolheu se encaixa nos padrões dos dados observados, dando a você mais confiança na sua escolha de modelo.

Os diagnósticos gráficos complementam os testes estatísticos, mostrando padrões que os números por si só podem não revelar. A análise residual ajuda a identificar desvios sistemáticos do comportamento esperado, enquanto os critérios de informação (AIC/BIC) equilibram a adequação do modelo em relação à complexidade. Basicamente, você quer um modelo que se encaixe bem sem ser desnecessariamente complicado.

Modelos de regressão e mistura

A regressão de Weibull coloca as variáveis explicativas direto nos parâmetros de distribuição, permitindo que você modele como fatores como temperatura, carga ou características do paciente afetam o comportamento de falha. Essa extensão é útil em testes de confiabilidade e pesquisas médicas, onde vários fatores influenciam os resultados.

Os modelos Weibull mistos lidam com populações com subgrupos distintos (como diferentes modos de falha) combinando várias distribuições Weibull. Pense numa população em que alguns itens quebram por desgaste, enquanto outros quebram por defeitos aleatórios. Você precisa de modelos diferentes para cada modo de falha.

As aplicações de machine learning usam cada vez mais esses modelos para reconhecimento de padrões complexos e aplicações de redes neurais, unindo métodos estatísticos tradicionais com técnicas modernas de IA.

Riscos concorrentes e modelos de degradação

Alguns sistemas vão enfrentar vários modos de falha ao mesmo tempo. Desgaste mecânico, falha elétrica e degradação ambiental podem ameaçar o mesmo componente. Os modelos de riscos concorrentes usam várias distribuições de Weibull para representar cada modo de falha, ajudando você a entender quais riscos são mais críticos.

Os modelos de degradação acompanham como o desempenho do sistema vai piorando com o tempo, usando distribuições de Weibull para modelar o tempo até que o desempenho caia abaixo dos limites aceitáveis. Isso é útil para sistemas em que você pode medir a degradação antes que ocorra uma falha completa.

Formulários relacionados e especiais

A distribuição inversa de Weibull mostra situações em que valores maiores são menos prováveis de acontecer, como resistência mínima em materiais ou tempos de sobrevivência mais curtos na biologia. Essa variante é útil quando as suposições tradicionais de Weibull não se encaixam nos seus padrões de dados.

As distribuições discretas de Weibull adaptam o modelo contínuo para dados de contagem, como o número de ciclos até a falha ou intervalos de tempo discretos em estudos de sobrevivência. Não é tão comum, mas é útil quando seus dados vêm em pedaços separados, em vez de medições contínuas.

Conclusão

A adaptabilidade da distribuição de Weibull a torna valiosa para analisar quando as coisas acontecem ao longo do tempo. Ele lida com taxas de risco crescentes, decrescentes ou estáveis e funciona bem com dados incompletos. Nossos cursos Análise de Sobrevivência em Python e Análise de Sobrevivência em R permitem que você pratique comconjuntos de dados e métodos já conhecidos.

As futuras direções de pesquisa incluem abordagens bayesianas que incorporam o conhecimento prévio de forma mais eficaz, híbridos de machine learning que combinam a modelagem de Weibull com redes neurais e aplicações de big data que adaptam os métodos tradicionais a conjuntos de dados massivos.