Weibull-Verteilung: Wie man Zeit-bis-zum-Ereignis-Daten modelliert

Wenn du analysierst, wie lange Dinge halten (egal ob es um die Lebensdauer von elektronischen Bauteilen, die Überlebenszeit von Patienten oder die Zuverlässigkeit von Geräten geht), brauchst du eine Verteilung, die mit der Komplexität von Ausfallmustern klarkommt. Die Weibull-Verteilung geht nicht davon aus, dass Ausfälle mit einer konstanten Rate passieren, wie es bei einfacheren Modellen der Fall ist. Stattdessen kann es Szenarien modellieren, in denen die Ausfallraten mit der Zeit steigen (wie bei Verschleißprozessen), anfangs sinken (wie bei der Beseitigung früher Herstellungsfehler) oder gleich bleiben.

Wenn du dich mit Wahrscheinlichkeitskonzepten noch nicht auskennst, dann ist unser Kurs „Grundlagen der Wahrscheinlichkeit in R“ genau das Richtige für dich.Hier lernst du die statistischen Grundlagen, die du für fortgeschrittene Verteilungsaufgaben brauchst. Dieses Tutorial zeigt dir die mathematischen Grundlagen der Weibull-Verteilung. Du lernst, wie man seine Parameter anhand von Daten schätzt, und siehst, wie seine Flexibilität ihn besonders nützlich für Zuverlässigkeitsanalysen und Überlebensstudien macht. Am Ende wirst du nicht nur die Theorie hinter dieser nützlichen Verteilung verstehen, sondern auch, wann und wie du sie auf deine eigenen Herausforderungen bei der Zeit-bis-zum-Ereignis-Analyse anwenden kannst.

Was ist die Weibull-Verteilung?

Die Weibull-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die für die Modellierung von Zeit-bis-zum-Ereignis-Daten entwickelt wurde. Du wirst es am häufigsten in der Fehleranalyse, in Überlebensstudien und in der Zuverlässigkeitstechnik finden, wo es darum geht, zu verstehen, „wann etwas passiert“. 

Was die Weibull-Verteilung von einfacheren Alternativen unterscheidet, ist ihre Anpassungsfähigkeit an verschiedene Ausfallmuster. Während manche Verteilungen davon ausgehen, dass Ereignisse regelmäßig und vorhersehbar passieren, kann die Weibull-Verteilung mit Situationen umgehen, in denen sich die Wahrscheinlichkeit von Ereignissen mit der Zeit ändert. Diese Flexibilität ist echt praktisch, wenn du mit komplizierten Systemen oder Prozessen arbeitest, bei denen die zugrunde liegenden Mechanismen nicht ganz klar sind.

Historischer Kontext und Grundprinzipien

Die Geschichte hinter dieser Verteilung fängt mit dem schwedischen Mathe-Genie Waloddi Weibull an, der sie in den 1930er Jahren entwickelt hat, als er sich mit Materialfestigkeit und Materialermüdung beschäftigt hat. Seine Arbeit hat den Grundstein für die moderne Zuverlässigkeitstechnik gelegt.

Die Verteilung gibt's in zwei Hauptformen, die unterschiedliche Analysezwecke erfüllen. Das Zwei-Parameter-Weibull-Modell nutzt Form- und Skalenparameter, um Situationen zu beschreiben, in denen Ereignisse sofort losgehen können. Die Version mit drei Parametern hat noch einen Standortparameter, der einen Mindestschwellenwert festlegt, bevor was passieren kann – das ist praktisch, um Systeme mit eingebauten Verzögerungen oder „Einlaufphasen” zu modellieren.

Die Weibull-Verteilung gehört zu einer Familie von verwandten Verteilungen, wobei die Exponentialverteilung ein Sonderfall ist. Diese Verbindung hilft zu erklären, warum Weibull- und Exponential smodelle im Zusammenhang mit Zuverlässigkeit oft miteinander verglichen werden. Die größere Flexibilität von Weibull macht es möglich, andere bekannte Verteilungen unter bestimmten Parameterbedingungen zu approximieren, was zu seiner weit verbreiteten Anwendung beiträgt.

Parameter der Weibull-Verteilung

Nachdem wir uns jetzt mit der historischen Entwicklung und dem grundlegenden Verhalten beschäftigt haben, schauen wir uns mal die Parameter an, die der Weibull-Verteilung ihre Flexibilität geben. Jeder Parameter gibt dir genaue Infos darüber, wie sich deine Daten verhalten.

Der Formparameter (k oder β) bestimmt, wie sich die Verteilung und die Hazard-Funktion verhalten. Wenn die Werte unter 1 liegen, hast du es mit Säuglingssterblichkeitsmustern zu tun, bei denen es aufgrund von Herstellungsfehlern zu frühen Ausfällen kommt. Wenn die Werte größer als 1 sind, siehst du Verschleißausfälle, bei denen Sachen durch den normalen Gebrauch mit der Zeit kaputtgehen.

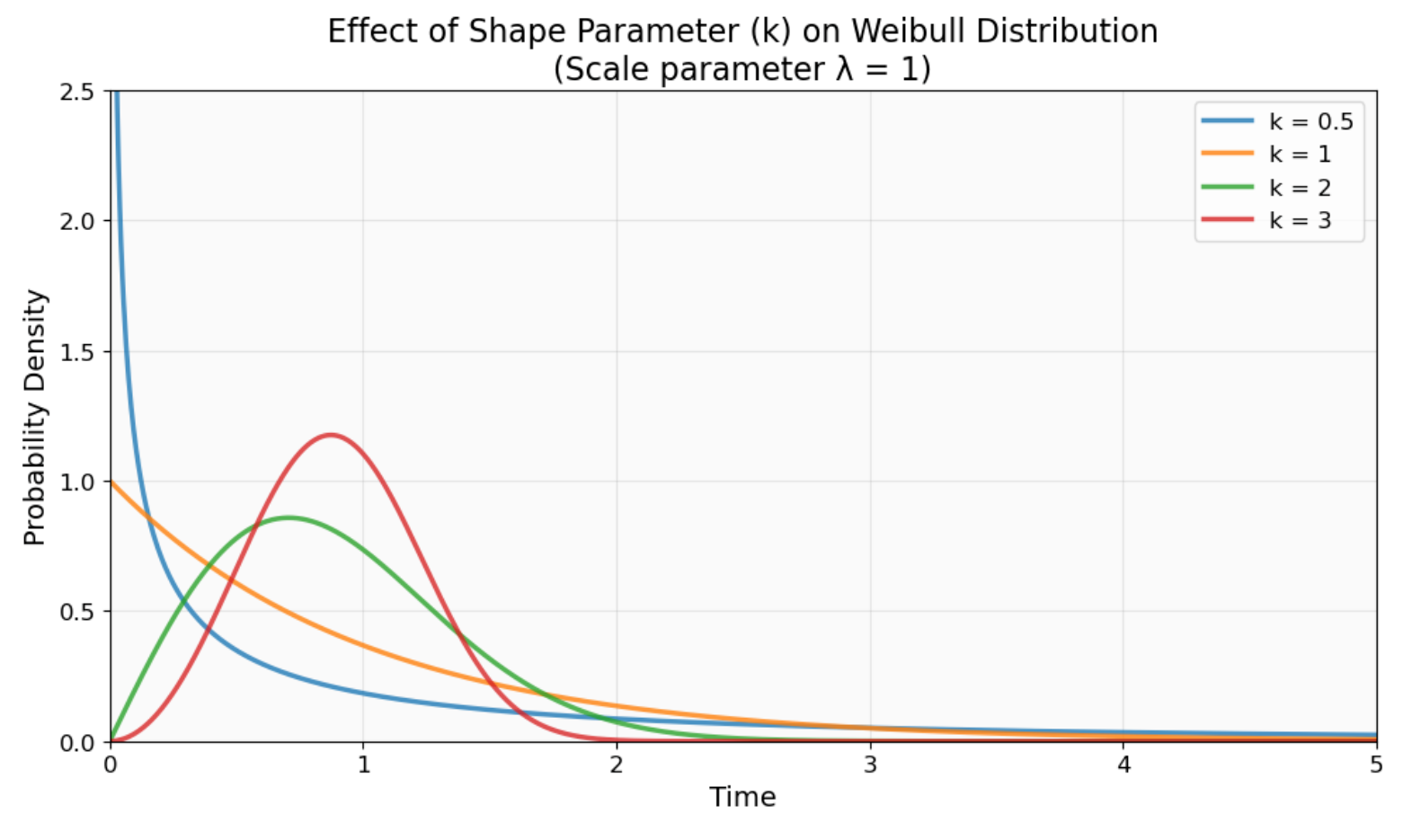
Wie der Formparameter (k) das Verhalten der Weibull-Verteilung beeinflusst. Schau mal, wie k < 1 eine hohe frühe Ausfallwahrscheinlichkeit erzeugt (blaue Kurve), k = 1 konstante Ausfallraten erzeugt (orange) und k > 1 mit der Zeit steigende Ausfallraten zeigt (grüne und rote Kurven). Bild vom Autor.

Der Skalenparameter (λ oder η) zeigt die charakteristische Lebensdauer an. Das ist der Zeitpunkt, an dem genau 63,2 % der Teile kaputt sein werden, egal wie der Formparameter ist. Du kannst das als typische Lebensdauer der Verteilung sehen, auch wenn der tatsächliche Mittelwert wegen der Form der Verteilung anders sein kann.

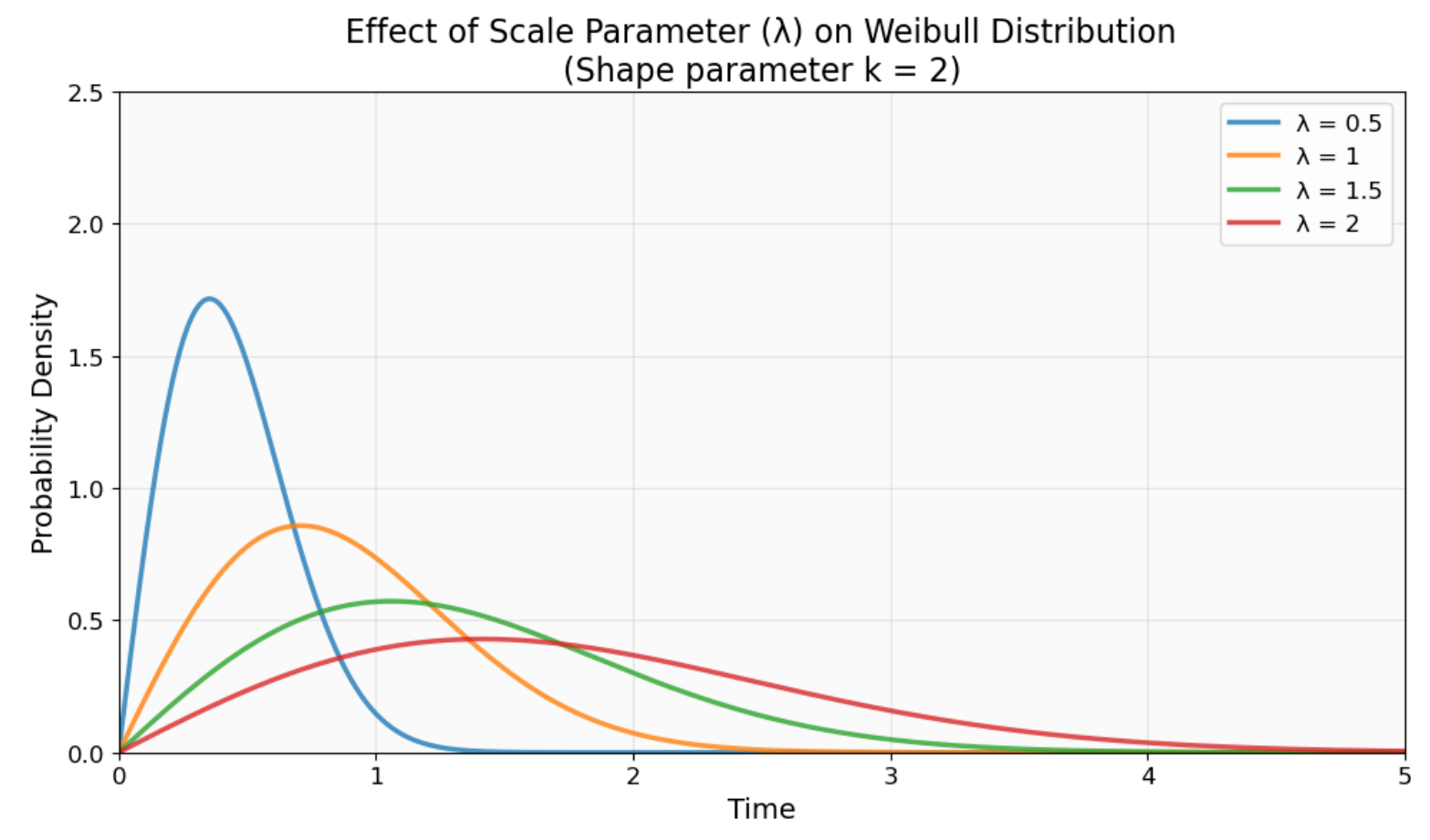
Wie der Skalenparameter (λ) die Weibull-Verteilung auf der Zeitachse verschiebt. Größere λ-Werte verschieben die Verteilung nach rechts (längere charakteristische Lebensdauer), während kleinere Werte sie nach links verschieben (kürzere charakteristische Lebensdauer). Die Form bleibt gleich. Bild vom Autor.

Bei Anwendungen mit drei Parametern verschiebt der Standortparameter (θ oder γ) die Verteilung entlang der Zeitachse. Es zeigt die garantierte Mindestlebensdauer an, bevor irgendwelche Ausfälle auftreten können. Das ist super, wenn du Systeme mit Einbrennzeiten oder Komponenten mit Garantiezeiten modellierst, bei denen ein vorzeitiger Ausfall unmöglich ist.

Verschiedene Fachgebiete benutzen unterschiedliche Notationen, daher kann man (k,λ) in der Zuverlässigkeitstechnik oder (β,η) in der Überlebensanalyse sehen. Die mathematischen Beziehungen bleiben gleich, egal welche Notation du siehst.

Mathematische Beschreibung und statistische Eigenschaften

Die mathematische Grundlage der Weibull-Verteilung liefert die Werkzeuge, die man für praktische Anwendungen braucht. Schauen wir uns mal die wichtigsten Funktionen an, die diese Distribution so nützlich machen.

Kernfunktionen und Kennzahlen

Die Wahrscheinlichkeitsdichtefunktion (PDF) zeigt, wie wahrscheinlich es ist, dass zu einem bestimmten Zeitpunkt ein Fehler auftritt. Für die Weibull-Verteilung ist das:

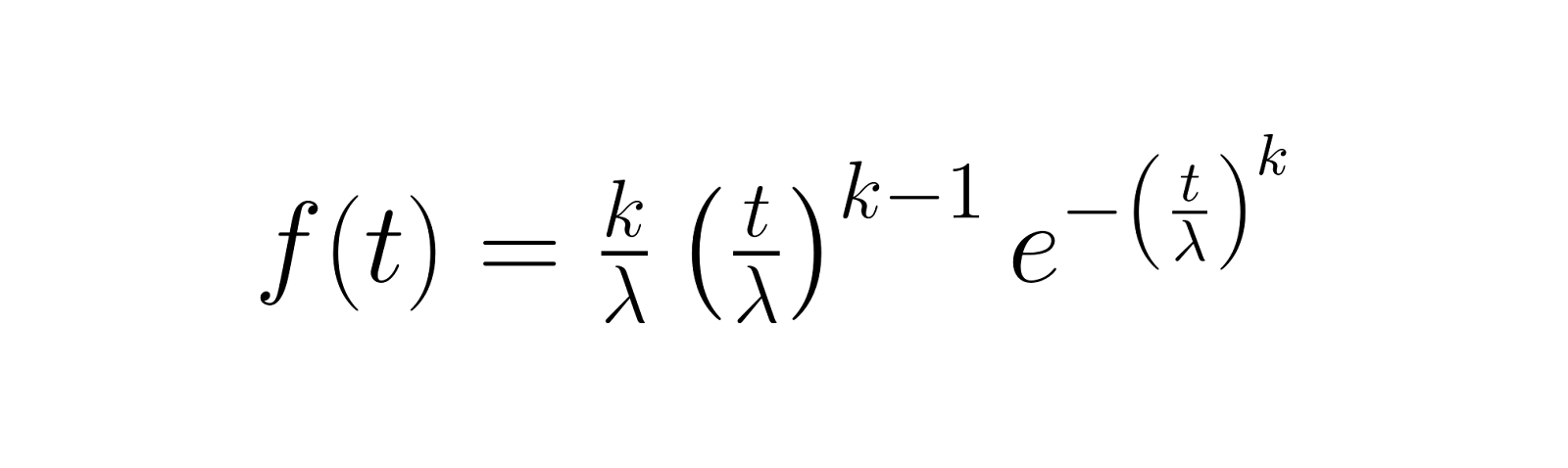
Diese Funktion zeigt, wie sich die Ausfallwahrscheinlichkeitsdichte mit der Zeit verändert, wobei der Formparameter k bestimmt, ob Ausfälle eher früh auftreten (k < 1), über die Zeit konstant bleiben (k = 1) oder mit zunehmendem Alter zunehmen (k > 1).

Die kumulative Verteilungsfunktion (CDF) gibt die Wahrscheinlichkeit an, mit der ein Ausfall bis zu einem bestimmten Zeitpunkt auftritt:

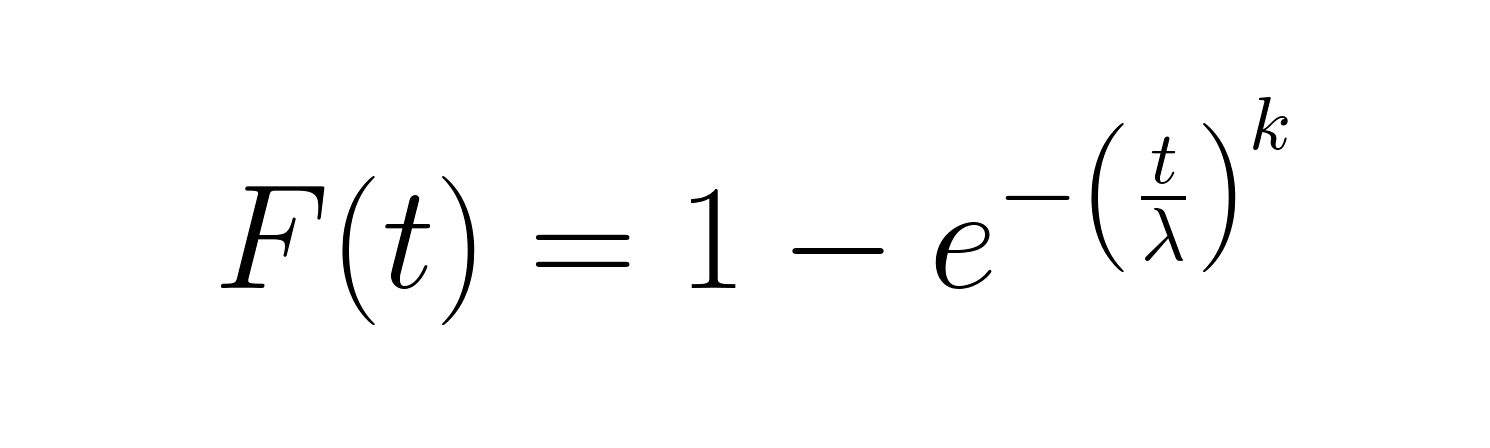
Diese Funktion eignet sich gut, um den Prozentsatz der Artikel zu berechnen, die voraussichtlich innerhalb eines bestimmten Zeitraums ausfallen werden. Die Zuverlässigkeitsfunktion (1-CDF) gibt dir die andere Seite und zeigt, wie hoch die Wahrscheinlichkeit ist, dass etwas nach der Zeit t noch funktioniert.

Die Hazard-Funktion zeigt die momentane Ausfallrate zu einem bestimmten Zeitpunkt:

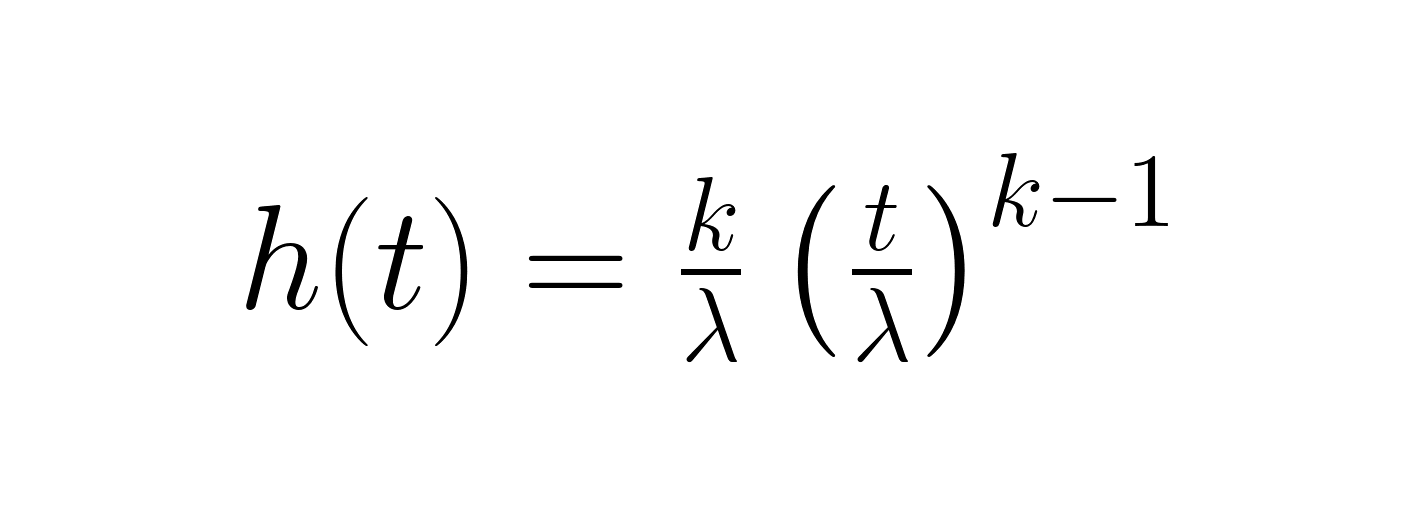
Diese Funktion ist wichtig, um zu verstehen, wie sich Risiken im Laufe der Zeit verändern. Wenn k < 1 ist, wird das Risiko kleiner (die Zuverlässigkeit wird besser), wenn k = 1 ist, bleibt es gleich, und wenn k > 1 ist, wird es größer (die Zuverlässigkeit wird schlechter). Die Überlebensfunktion, die genau wie die Zuverlässigkeitsfunktion ist, zeigt die Wahrscheinlichkeit, dass etwas länger als eine bestimmte Zeit hält.

Statistische Momente zeigen, wie die Verteilung im Durchschnitt aussieht und wie stark sie schwankt. Der Mittelwert hat mit der Gammafunktion zu tun und hängt von beiden Parametern ab, was ihn komplizierter macht als die charakteristische Lebensdauer. Die Varianz zeigt, wie weit die Werte vom Mittelwert entfernt sind, während der Median bei schiefen Verteilungen oft eine intuitivere Interpretation ermöglicht als der Mittelwert. Der Modus zeigt die wahrscheinlichste Ausfallzeit an, auch wenn er vielleicht nicht für alle Parameterkombinationen da ist.

Die Momentgenerierungsfunktion fasst alle statistischen Momente in einem einzigen Ausdruck zusammen, während die Entropie die Unsicherheit oder den Informationsgehalt der Verteilung misst. Diese Eigenschaften und die Muster des Ausfallverhaltens machen die Weibull-Verteilung super für die Modellierung von verschiedenen realen Phänomenen, bei denen einfache exponentielle Annahmen nicht ausreichen.

Bedingte Zuverlässigkeit und Perzentile

Berechnungen zur bedingten Zuverlässigkeit klären praktische Fragen wie „Wenn dieses Teil schon 1000 Stunden durchgehalten hat, wie hoch ist die Wahrscheinlichkeit, dass es noch weitere 500 Stunden hält?“ Dabei wird die Wahrscheinlichkeit berechnet, dass jemand nach dem aktuellen Zeitpunkt noch eine bestimmte Zeit weiterlebt. Die Berechnung geht so:

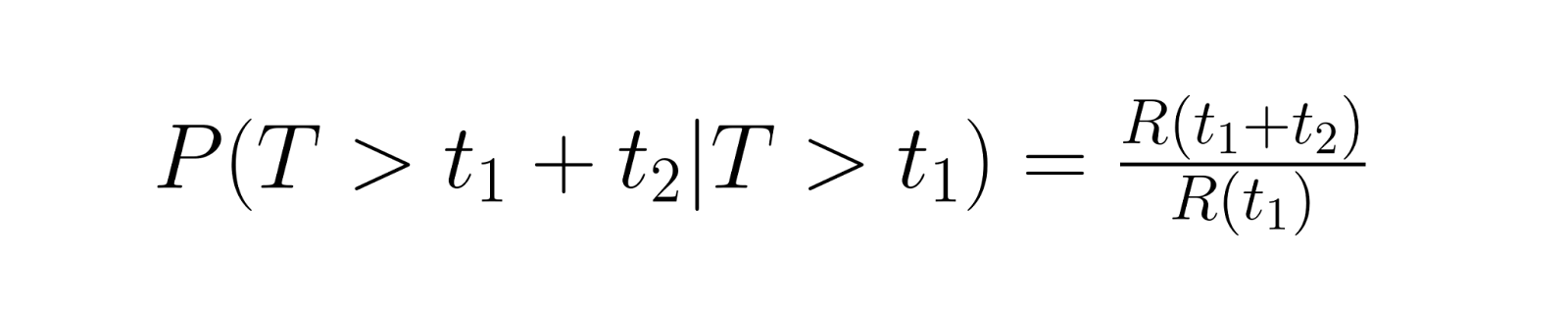
wobei R(t) die Zuverlässigkeitsfunktion ist.

Perzentile helfen dabei, wichtige Kennzahlen für die gesamte Lebensdauer zu schätzen, die für Geschäftsentscheidungen wichtig sind. Die B₁₀-Lebensdauer zeigt an, wann 10 % der Teile kaputt sein werden, während die B₉₀-Lebensdauer sagt, wann 90 % der Teile kaputt sein werden. Diese Prozentwerte sind super wichtig für die Garantieanalyse, die Wartungsplanung und die Risikobewertung.

Die Prozentpunktfunktion (inverse CDF) gibt dir eine direkte Quantilsschätzung, indem sie F(t) = p für jede gewünschte Wahrscheinlichkeit p berechnet. Diese Funktion wandelt kumulative Wahrscheinlichkeiten wieder in Zeitwerte um, sodass du bestimmte Ausfallzeiten für bestimmte Zuverlässigkeitsniveaus bestimmen kannst. Die meisten Statistikprogramme haben eingebaute Funktionen für diese Berechnungen, was die Schätzung von Perzentilen einfach macht, sobald du die Weibull-Parameter geschätzt hast.

Methoden zur Parameterschätzung

Die mathematischen Eigenschaften zu verstehen ist eine Sache, aber wie ermittelt man diese Parameter tatsächlich aus den Daten? Um Weibull-Parameter aus Daten zu schätzen, musst du die richtige Methode für deine Situation und die Eigenschaften deiner Daten auswählen. Jeder Ansatz hat seine eigenen Vorteile und Einschränkungen.

Maximalwahrscheinlichkeitsschätzung (MLE)

MLE bietet den statistisch strengsten Ansatz für die Parameterschätzung. Es findet Parameterwerte, die die Wahrscheinlichkeit maximieren, dass deine tatsächlichen Daten beobachtet werden, was es bei vollständigen Datensätzen effektiv macht. Stell dir vor, du suchst die Parameter, die deine beobachteten Daten „am wahrscheinlichsten“ machen.

Die Methode geht mit zensierten Daten um (wo du weißt, dass die Elemente bis zu einem bestimmten Zeitpunkt überlebt haben, aber nicht genau wann sie ausgefallen sind) mithilfe spezieller Algorithmen. Das ist bei Zuverlässigkeitstests echt praktisch, wo man nicht immer warten kann, bis alle Teile kaputt gehen. ​Die meisten Statistikprogramme haben MLE-Routinen, die extra für die Weibull-Analyse entwickelt wurden. Auch wenn die Rechenkomplexität mit der Größe des Datensatzes steigt, können moderne Implementierungen Datensätze mit Hunderttausenden von Beobachtungen gut verarbeiten.

Momentemethode (MOM)

Der MOM-Ansatz schätzt Parameter, indem er theoretische Momente mit den Momenten aus deinen Daten abgleicht. Obwohl es statistisch gesehen nicht so effizient ist wie MLE, ist es einfach zu berechnen und liefert oft gute erste Schätzungen für komplexere Methoden.

Dieser Ansatz ist super, wenn du schnelle Schätzungen brauchst oder mit Daten arbeitest, die nicht ganz zu den MLE-Annahmen passen. Es ist auch nützlich, um einen groben Überblick über deine Parameter zu bekommen, bevor du dich in komplexere Analysen stürzt.

Kleinste Quadrate und grafische Techniken

Weibull-Wahrscheinlichkeitsdiagramme zeigen Daten auf logarithmischen Koordinaten, wo Weibull-Verteilungen wie gerade Linien aussehen. So kannst du die Modellanpassung visuell checken, während du die Parameter durch lineare Regression schätzt. Die Methode nutzt speziell skaliertes Millimeterpapier (heutzutage digital in Software reproduziert) mit einer doppelt-logarithmischen Transformation, die die kumulative Verteilungsfunktion von Weibull linearisiert.

Der Prozess umfasst die Rangfolge deiner Ausfalldaten vom kleinsten zum größten Wert, die Berechnung der mittleren Rangpositionen für jeden Datenpunkt (die die kumulative Ausfallwahrscheinlichkeit schätzen) und die Darstellung der Ausfallzeiten gegenüber diesen Wahrscheinlichkeiten. Wenn deine Daten einer Weibull-Verteilung folgen, bilden die Punkte ungefähr eine gerade Linie, deren Steigung dem Formparameter entspricht und deren Position den Skalenparameter bestimmt. Es ist zwar altmodisch, aber es funktioniert und das visuelle Feedback ist echt hilfreich, um deine Daten zu verstehen. Wenn die Punkte stark von der Linearität abweichen, könnte das bedeuten, dass das Weibull-Modell für deinen Datensatz nicht so gut passt. Deshalb ist diese Technik sowohl für die Parameterschätzung als auch für die Modellvalidierung super nützlich.

Drei-Parameter-Herausforderungen

Die Schätzung des Standortparameters θ ist echt schwierig, weil er die untere Grenze der Verteilung beeinflusst. Die Standard-MLE kann unzuverlässige Schätzungen liefern, wenn θ sich der minimalen beobachteten Ausfallzeit nähert.

Profilwahrscheinlichkeitsmethoden lösen diese Schätzprobleme, indem sie θ als Störparameter behandeln und so stabilere Schätzungen für die Form- und Skalenparameter liefern. Es ist ein bisschen komplizierter, aber oft wichtig, um zuverlässige Ergebnisse zu kriegen.

Anwendungen in verschiedenen Fachbereichen

Die Vielseitigkeit der Weibull-Verteilung zeigt sich in ihren Anwendungen in verschiedenen Bereichen. Jeder Bereich nutzt bestimmte Aspekte der Flexibilität des Vertriebs.

Zuverlässigkeitstechnik

Zuverlässigkeitsingenieure nutzen die Weibull-Analyse für beschleunigte Lebensdauertests, bei denen Produkte unter Stressbedingungen getestet werden, um die normale Lebensdauer vorherzusagen. Anstatt jahrelang abzuwarten, um zu sehen, wie lange etwas hält, kannst du es einem Stresstest unterziehen und die Ergebnisse auf normale Bedingungen übertragen.

Die Garantieanalyse nutzt Weibull-Modelle, um zukünftige Schadensfälle zu schätzen und passende Deckungszeiträume festzulegen. Firmen müssen wissen, wie viele Produkte innerhalb der Garantiezeit kaputtgehen, um ihre Preise richtig festzulegen.

Die Planung der vorbeugenden Wartung profitiert von der Fähigkeit von Weibull, sich ändernde Ausfallraten über den Lebenszyklus von Geräten zu modellieren. Im Gegensatz zu Modellen, die von konstanten Ausfallraten ausgehen, zeigt dir Weibull, wann die Ausfallraten steigen, sodass du Wartungsarbeiten planen kannst, bevor es zu Ausfällen kommt.

Medizinische und biologische Wissenschaften

In der medizinischen Forschung werden bei der Überlebensanalyse oft Weibull-Modelle benutzt, um die Wirksamkeit von Behandlungen und die Prognose für Patienten zu untersuchen. Die Verteilung geht ganz normal mit zensierten Daten um, die man oft in klinischen Studien sieht, wo Patienten die Studie verlassen können, bevor das Ereignis passiert, das uns interessiert.

Die Weibull-Regression erweitert die grundlegende Analyse, indem sie Patientenmerkmale (Alter, Behandlungsart, Krankheitsstadium) als Kovariablen einbezieht. Das liefert personalisierte Überlebensprognosen, die für die Behandlungsplanung wichtig sind, und hilft Ärzten dabei, Patienten realistische Erwartungen hinsichtlich ihrer Prognose zu vermitteln.

Materialwissenschaft und Forstwirtschaft

Materialingenieure nutzen Weibull-Verteilungen, um die Festigkeit von spröden Materialien wie Keramik und Verbundwerkstoffen zu modellieren, bei denen das schwächste Glied das gesamte Versagen bestimmt. Die Fähigkeit der Verteilung, Extremwerte zu modellieren, macht sie perfekt für Anwendungen, bei denen es um Worst-Case-Szenarien geht.

In der Forstwirtschaft werden Weibull-Modelle für Baumdurchmesserverteilungen genutzt, um Ernteerträge vorherzusagen und nachhaltige Forstwirtschaft zu planen. Es ist eine praktische Anwendung, die dabei hilft, wirtschaftliche und ökologische Belange in Einklang zu bringen.

Windenergie und Umweltstudien

Dieser Artikel geht zwar hauptsächlich auf Anwendungen im Bereich „Time-to-Event“ ein, aber Weibull-Verteilungen können auch andere Sachen in der Umwelttechnik modellieren. Bei der Bewertung der Windressourcen wird Weibull benutzt, um die Windgeschwindigkeitsmuster an potenziellen Standorten für Windkraftanlagen zu beschreiben. Dabei zeigen die Formparameter, wie beständig der Wind für die Planung der Energieerzeugung ist.

Fortgeschrittene Themen und Erweiterungen

So nützlich diese Standardanwendungen auch sind, moderne Probleme erfordern oft mehr als nur eine einfache Weibull-Analyse. 

Modellauswahl und Anpassungsgüte

Die Entscheidung zwischen der Weibull-Verteilung und anderen Verteilungen braucht systematische Tests mit Hilfe von Anpassungsgüte-Statistiken wie dem Kolmogorov-Smirnov- und dem Anderson-Darling-Test. Diese Tests zeigen, wie gut die von dir gewählte Verteilung zu den beobachteten Datenmustern passt, sodass du dir bei der Wahl deines Modells sicher sein kannst.

Grafische Diagnosen ergänzen statistische Tests, indem sie Muster aufzeigen, die man mit Zahlen allein vielleicht übersehen würde. Die Residuenanalyse hilft dabei, systematische Abweichungen vom erwarteten Verhalten zu erkennen, während Informationskriterien (AIC/BIC) die Modellanpassung gegen die Komplexität abwägen. Du willst im Grunde ein Modell, das gut passt, ohne unnötig kompliziert zu sein.

Regressions- und Mischmodelle

Die Weibull-Regression bezieht erklärende Variablen direkt in die Verteilungsparameter ein, sodass du modellieren kannst, wie Faktoren wie Temperatur, Belastung oder Patientenmerkmale das Ausfallverhalten beeinflussen. Diese Erweiterung ist super für Zuverlässigkeitstests und medizinische Forschung, wo viele Faktoren die Ergebnisse beeinflussen.

Weibull-Mischmodelle können mit Gruppen mit unterschiedlichen Untergruppen (wie verschiedenen Ausfallmodi) umgehen, indem sie mehrere Weibull-Verteilungen kombinieren. Stell dir eine Population vor, in der manche Teile durch Verschleiß kaputtgehen, während andere wegen zufälliger Fehler ausfallen. Du brauchst für jeden Fehlermodus unterschiedliche Modelle.

Machine-Learning-Anwendungen nutzen diese Modelle immer öfter für komplexe Mustererkennung und neuronale Netzwerke und verbinden so traditionelle statistische Methoden mit modernen KI-Techniken.

Konkurrierende Risiken und Degradationsmodelle

Einige Systeme werden gleichzeitig mit mehreren Ausfallmodi konfrontiert sein. Mechanischer Verschleiß, elektrische Ausfälle und Umwelteinflüsse können alle dasselbe Bauteil gefährden. Konkurrierende Risikomodelle nutzen mehrere Weibull-Verteilungen, um jeden Ausfallmodus darzustellen, und helfen dir so zu verstehen, welche Risiken am kritischsten sind.

Degradationsmodelle zeigen, wie die Systemleistung mit der Zeit nachlässt, indem sie Weibull-Verteilungen nutzen, um die Zeit zu modellieren, bis die Leistung unter akzeptable Schwellenwerte fällt. Das ist praktisch für Systeme, bei denen man Verschleiß messen kann, bevor sie komplett kaputtgehen.

Verwandte und spezielle Formen

Die inverse Weibull-Verteilung beschreibt Situationen, in denen größere Werte seltener vorkommen, wie zum Beispiel die Mindestfestigkeit von Materialien oder die kürzesten Überlebenszeiten in der Biologie. Diese Variante ist nützlich, wenn die üblichen Weibull-Annahmen nicht zu deinen Datenmustern passen.

Diskrete Weibull-Verteilungen passen das kontinuierliche Modell für Zähldaten an, wie zum Beispiel die Anzahl der Zyklen bis zum Ausfall oder diskrete Zeitintervalle in Überlebensstudien. Das ist zwar nicht so häufig, aber praktisch, wenn deine Daten in einzelnen Blöcken statt als fortlaufende Messungen vorliegen.

Fazit

Die Weibull-Verteilung ist super praktisch, um zu analysieren, wann Sachen im Laufe der Zeit passieren. Es kann steigende, fallende oder gleichbleibende Gefahrenraten verarbeiten und funktioniert auch mit unvollständigen Daten gut. In unseren Kursen „Überlebensanalyse in Python“ und „Überlebensanalyse in R“ kannst du mitDatensätzen und bewährten Methoden üben.

Zukünftige Forschungsrichtungen umfassen Bayes'sche Ansätze, die Vorwissen effektiver einbeziehen, hybride Methoden des maschinellen Lernens, die Weibull-Modellierung mit neuronalen Netzen kombinieren, und Big-Data-Anwendungen, die traditionelle Methoden auf riesige Datensätze skalieren.