Tutoriel sur l'optimiseur AdamW dans PyTorch

Les algorithmes d'optimisation jouent un rôle crucial dans l'apprentissage profond : ils affinent les poids des modèles pour minimiser les fonctions de perte pendant la formation. L'un de ces algorithmes est l'optimiseur optimiseur Adam.

Adam est devenu extrêmement populaire dans le domaine de l'apprentissage profond en raison de sa capacité à combiner les avantages du momentum et des taux d'apprentissage adaptatifs. Il est donc très efficace pour la formation de réseaux neuronaux profonds. Elle nécessite également un réglage minimal des hyperparamètres, ce qui la rend largement accessible et efficace pour diverses tâches.

En 2017, Ilya Loshchilov et Frank Hutter ont présenté une version plus avancée de l'algorithme populaire d'Adam dans leur article "Régularisation par décroissance pondérale découplée."Ils l'ont nommé AdamW, qui se distingue par le découplage de la décroissance des poids du processus de mise à jour du gradient. Cette séparation est une amélioration cruciale par rapport à Adam et permet une meilleure généralisation du modèle.

AdamW est devenu de plus en plus important dans les applications modernes d'apprentissage profond, en particulier dans le traitement des modèles à grande échelle. Sa capacité supérieure à réguler les mises à jour de poids a contribué à son adoption dans des tâches exigeant des performances et une stabilité élevées. 

Dans ce tutoriel, nous allons aborder les principales différences entre Adam et AdamW, ainsi que les différents cas d'utilisation, et nous allons mettre en place un guide étape par étape pour implémenter AdamW dans PyTorch.

Adam vs AdamW

Adam et AdamW sont tous deux des optimiseurs adaptatifs largement utilisés dans l'apprentissage profond. La grande différence entre eux est la manière dont ils gèrent la régularisation des poids, ce qui a un impact sur leur efficacité dans différents scénarios. 

Alors qu'Adam combine le momentum et les taux d'apprentissage adaptatifs pour offrir une optimisation efficace, il incorpore la régularisation L2 d'une manière qui peut nuire à la performance. AdamW résout ce problème en découplant la décroissance des poids de la mise à jour du taux d'apprentissage, ce qui constitue une approche plus efficace pour les modèles de grande taille et améliore la généralisation. La décroissance des poids, une forme de régularisation L2, pénalise les poids importants dans le modèle. Adam intègre la décroissance du poids dans le processus de mise à jour du gradient, tandis qu'AdamW l'applique séparément après la mise à jour du gradient.

Voici quelques autres différences : 

Principales différences entre Adam et AdamW

Bien que les deux optimiseurs soient conçus pour gérer l'élan et ajuster les taux d'apprentissage de manière dynamique, ils diffèrent fondamentalement dans leur traitement de la décroissance des poids. 

Dans Adam, la décroissance des poids est appliquée indirectement dans le cadre de la mise à jour du gradient, ce qui peut modifier involontairement la dynamique d'apprentissage et interférer avec le processus d'optimisation. AdamW, cependant, sépare la décroissance du poids de l'étape du gradient, ce qui garantit que la régularisation a un impact direct sur les paramètres sans altérer le mécanisme d'apprentissage adaptatif. 

Cette conception permet une régularisation plus précise, ce qui aide les modèles à mieux se généraliser, en particulier dans les tâches qui impliquent des ensembles de données vastes et complexes. Par conséquent, les deux optimiseurs ont souvent des cas d'utilisation très différents.  

Cas d'utilisation pour Adam

Adam est plus performant dans les tâches où la régularisation est moins critique ou lorsque l'efficacité des calculs est prioritaire par rapport à la généralisation. En voici quelques exemples :

• Réseaux neuronaux plus petits. Pour des tâches telles que la classification d'images de base à l'aide de petitsréseaux neuronaux convolutifs (CNN) sur des ensembles de données tels que MNIST ou CIFAR-10, où la complexité du modèle est faible, Adam peut optimiser efficacement sans avoir besoin d'une régularisation importante.
• Problèmes de régression simple. Dans les tâches de régression simples avec des ensembles de caractéristiques limités, telles que la prédiction des prix de l'immobilier à l'aide d'un modèle de régression linéaire, Adam peut converger rapidement sans nécessiter de techniques de régularisation avancées.
• Prototypage à un stade précoce. Au cours des premières étapes du développement du modèle, où une expérimentation rapide est nécessaire, Adam permet des itérations rapides sur des architectures plus simples, ce qui permet aux chercheurs d'identifier les problèmes potentiels sans avoir à régler les paramètres de régularisation.
• Des données moins bruyantes. Lorsque vous travaillez avec des ensembles de données propres avec un minimum de bruit, comme des données textuelles bien classées pour l'analyse des sentiments, Adam peut apprendre efficacement des modèles sans le risque de surajustement qui pourrait nécessiter une régularisation plus lourde.
• Cycles d'entraînement courts. Dans les scénarios soumis à des contraintes de temps, tels que le déploiement rapide de modèles pour des applications en temps réel, l'optimisation efficace d'Adam peut permettre d'obtenir rapidement des résultats satisfaisants, même s'ils ne sont pas entièrement optimisés pour la généralisation.

Cas d'utilisation d'AdamW

AdamW excelle dans les scénarios où le surajustement est un problème et où la taille du modèle est importante. Par exemple : 

• Grands transformateurs. Dans les tâches de traitement du langage naturel, telles que l'ajustement fin de modèles comme GPT sur de vastes corpus de textes, la capacité d'AdamW à gérer la décroissance des poids empêche efficacement l'ajustement excessif, garantissant ainsi une meilleure généralisation.
• Modèles complexes de vision par ordinateur. Pour les tâches impliquant des réseaux neuronaux convolutionnels profonds (CNN) formés sur de grands ensembles de données comme ImageNet, AdamW aide à maintenir la stabilité et la performance du modèle en découplant la décroissance des poids, ce qui est crucial pour obtenir une grande précision.
• Apprentissage multitâche. Dans les scénarios où un modèle est entraîné sur plusieurs tâches simultanément, AdamW offre la flexibilité nécessaire pour gérer divers ensembles de données et éviter le surajustement sur une seule tâche.
• Modèles génératifs. Pour l'apprentissage des réseaux adversaires génératifs (GAN), où le maintien d'un équilibre entre le générateur et le discriminateur est essentiel, la régularisation améliorée d'AdamW peut aider à stabiliser l'apprentissage et à améliorer la qualité des résultats générés.
• Apprentissage par renforcement. Dans les applications d'apprentissage par renforcement où les modèles doivent s'adapter à des environnements complexes et apprendre des politiques robustes, AdamW permet d'atténuer l'adaptation excessive à des états ou des actions spécifiques, améliorant ainsi les performances générales du modèle dans des situations variées.

Avantages d'AdamW par rapport à Adam

Mais pourquoi quelqu'un voudrait-il utiliser AdamW plutôt qu'Adam ? Simple. AdamW offre plusieurs avantages clés qui améliorent ses performances, en particulier dans les scénarios de modélisation complexes. 

Il répond à certaines des limites de l'optimiseur Adam, ce qui le rend plus efficace en matière d'optimisation et contribue à améliorer la formation et la robustesse des modèles. 

Voici quelques-uns des avantages les plus marquants :

• Décroissance pondérale découplée. En séparant la décroissance des poids des mises à jour du gradient, AdamW permet un contrôle plus précis de la régularisation, ce qui conduit à une meilleure généralisation du modèle.
• Généralisation améliorée. AdamW réduit le risque de surajustement, en particulier dans les modèles à grande échelle, ce qui le rend adapté aux tâches impliquant des ensembles de données étendus et des architectures complexes.
• Stabilité pendant l'entraînement. La conception d'AdamW permet de maintenir la stabilité tout au long du processus d'apprentissage, ce qui est essentiel pour les modèles qui nécessitent un réglage minutieux de leurs hyperparamètres.
• Évolutivité. AdamW est particulièrement efficace pour la mise à l'échelle des modèles, car il peut gérer la complexité accrue des réseaux profonds sans sacrifier les performances, ce qui lui permet d'être appliqué dans des architectures de pointe.

Comment fonctionne AdamW

La force principale d'AdamW réside dans son approche de la décroissance des poids, qui est découplée des mises à jour adaptatives du gradient typiques d'Adam. Cet ajustement garantit que la régularisation est appliquée directement aux poids du modèle, ce qui améliore la généralisation sans avoir d'impact négatif sur la dynamique du taux d'apprentissage.

L'optimiseur s'appuie sur la nature adaptative d'Adam, en conservant les avantages de l'élan et des ajustements du taux d'apprentissage par paramètre. L'application indépendante de la décroissance des poids permet de remédier à l'un des principaux défauts d'Adam : sa tendance à affecter les mises à jour du gradient au cours de la régularisation. Cette séparation permet à AdamW de maintenir un apprentissage stable, même dans les modèles complexes et à grande échelle, tout en contrôlant l'overfitting.

Dans les sections suivantes, nous explorerons la théorie qui sous-tend la décroissance des poids et la régularisation, ainsi que les mathématiques qui sous-tendent le processus d'optimisation d'AdamW.

Théorie de la décroissance des poids et de la régularisation L2

La régularisation L2 est une technique utilisée pour éviter l'ajustement excessif. Il atteint cet objectif en ajoutant un terme de pénalité à la fonction de perte, décourageant les valeurs de poids élevées. Cette technique permet de créer des modèles plus simples qui s'adaptent mieux aux nouvelles données. 

Dans les optimiseurs traditionnels, tels qu'Adam, la décroissance des poids est appliquée dans le cadre de la mise à jour du gradient, ce qui affecte par inadvertance les taux d'apprentissage et peut conduire à des performances sous-optimales.

AdamW améliore cette méthode en découplant la décroissance du poids du calcul du gradient. En d'autres termes, au lieu d'appliquer la décroissance des poids pendant la mise à jour du gradient, AdamW la traite comme une étape distincte, en l'appliquant directement aux poids après la mise à jour du gradient. Cela empêche la dégradation des poids d'interférer avec le processus d'optimisation, ce qui permet d'obtenir une formation plus stable et une meilleure généralisation.

Fondement mathématique d'AdamW

AdamW modifie l'optimiseur Adam traditionnel en changeant la façon dont la décroissance du poids est appliquée. Les équations de base d'AdamW peuvent être représentées comme suit :

1. Momentum et taux d'apprentissage adaptatif : Comme Adam, AdamW utilise le momentum et les taux d'apprentissage adaptatifs pour calculer les mises à jour des paramètres sur la base des moyennes mobiles des gradients et des gradients au carré.

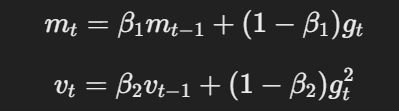
L'équation pour le momentum et le taux d'apprentissage adaptatif

2. Estimations corrigées des biais:Les estimations du premier et du second moment sont corrigées pour tenir compte du biais à l'aide de la méthode suivante :

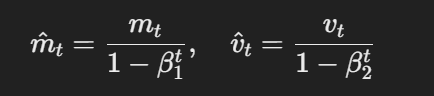
La formule pour les estimations corrigées du biais

3. Mise à jour des paramètres avec décroissance découplée des poids : Dans AdamW, la décroissance des poids est appliquée directement aux paramètres après la mise à jour du gradient. La règle de mise à jour est la suivante :

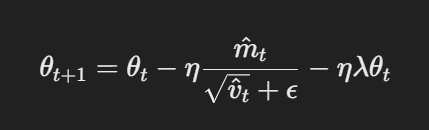
Mise à jour des paramètres avec décroissance découplée des poids

Ici, η est le taux d'apprentissage, λ est le facteur de décroissance du poids, et θt représente les paramètres. Ce terme découplé de décroissance du poids λθt garantit que la régularisation est appliquée indépendamment de la mise à jour du gradient, ce qui constitue la principale différence avec Adam.

Mise en œuvre d'AdamW dans PyTorch

Implémentation d'AdamW dans PyTorch est simple ; cette section fournit un guide complet pour le mettre en place. Suivez les étapes suivantes pour apprendre à affiner les modèles de manière efficace avec Adam Optimizer. 

Un guide pas à pas pour AdamW dans PyTorch

Note : ce tutoriel suppose que vous avez déjà installé PyTorch. Reportez-vous à la documentation pour obtenir des conseils.

Étape 1 : Importez les bibliothèques nécessaires

import torch
import torch.nn as nn
import torch.optim as optim
Import torch.nn.functional as F

Étape 2 : Définir le modèle

class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1)
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2, padding=0) 
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1) 
        self.fc1 = nn.Linear(64 * 8 * 8, 128) 
        self.fc2 = nn.Linear(128, 10) 

    def forward(self, x): 
        x = self.pool(F.relu(self.conv1(x))) 
        x = self.pool(F.relu(self.conv2(x))) 
        x = x.view(-1, 64 * 8 * 8) 
        x = F.relu(self.fc1(x)) 
        x = self.fc2(x) 

Étape 3 : Définir les hyperparamètres 

learning_rate = 1e-4
weight_decay = 1e-2
num_epochs = 10 # number of epochs

Étape 4 : Initialiser l'optimiseur AdamW et définir la fonction de perte

optimizer = optim.AdamW(model.parameters(), lr=learning_rate, weight_decay=weight_decay) 
criterion = nn.CrossEntropyLoss()

Voilà ! 

Vous êtes maintenant prêt à former votre modèle CNN, et c'est ce que nous allons faire dans la section suivante. 

Exemple pratique : Affiner un modèle à l'aide d'AdamW

Ci-dessus, nous avons défini le modèle, défini les hyperparamètres, initialisé l'optimiseur (AdamW) et défini la fonction de perte. 

Pour entraîner le modèle, nous devons importer quelques modules supplémentaires ; 

from torch.utils.data import DataLoader # provides an iterable of the dataset
import torchvision
import torchvision.transforms as transforms

Définissez ensuite le jeu de données et les chargeurs de données. Pour cet exemple, nous utiliserons l'ensemble de données CIFAR-10 : 

# Define transformations for the training set
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])
# Load CIFAR-10 dataset
train_dataset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
val_dataset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
# Create data loaders
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)

Puisque nous avons déjà défini notre modèle, l'étape suivante consiste à mettre en œuvre la boucle d'apprentissage afin d'optimiser le modèle à l'aide d'AdamW. 

Voici à quoi cela ressemble : 

for epoch in range(num_epochs):
    model.train()  # Set the model to training mode
    running_loss = 0.0
    for inputs, labels in train_loader:
        optimizer.zero_grad()  # Clear gradients
        outputs = model(inputs)  # Forward pass
        loss = criterion(outputs, labels)  # Calculate loss
        loss.backward()  # Backward pass
        optimizer.step()  # Update weights
        running_loss += loss.item()
    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {running_loss/len(train_loader):.4f}')

La dernière étape consiste à valider les performances du modèle sur l'ensemble de données de validation que nous avons créé précédemment. 

Voici le code : 

model.eval()  # Set the model to evaluation mode
correct = 0
total = 0
with torch.no_grad():
    for inputs, labels in val_loader:
        outputs = model(inputs)  # Forward pass
        _, predicted = torch.max(outputs.data, 1)  # Get predicted class
        total += labels.size(0)  # Update total samples
        correct += (predicted == labels).sum().item()  # Update correct predictions
accuracy = 100 * correct / total
print(f'Validation Accuracy: {accuracy:.2f}%')

Et voilà. 

Vous savez maintenant comment mettre en œuvre AdamW dans PyTorch. 

Cas d'utilisation courants pour AdamW

Nous avons donc établi qu'AdamW a gagné en popularité grâce à sa gestion plus efficace de la perte de poids que son prédécesseur, Adam. 

Mais quels sont les cas d'utilisation courants de cet optimiseur ? 

Nous y reviendrons dans cette section... 

Modèles d'apprentissage profond à grande échelle

AdamW est particulièrement utile pour l'apprentissage de grands modèles tels que BERT, GPT et d'autres architectures de transformateurs. Ces modèles comportent généralement des millions, voire des milliards de paramètres, ce qui signifie souvent qu'ils nécessitent des algorithmes d'optimisation efficaces qui gèrent des mises à jour de poids complexes et des défis de généralisation.

Tâches de vision par ordinateur et de NLP

AdamW est devenu l'optimiseur de choix pour les tâches de vision par ordinateur impliquant des CNN et des tâches de NLP impliquant des transformateurs. Sa capacité à éviter l'ajustement excessif en fait un outil idéal pour les tâches impliquant de grands ensembles de données et des architectures complexes. Le découplage de la décroissance des poids permet à AdamW d'éviter les problèmes rencontrés par Adam lors de la régularisation excessive des modèles.

Optimisation des hyperparamètres dans AdamW

L'ajustement des hyperparamètres est le processus de sélection des meilleures valeurs pour les paramètres qui régissent l'apprentissage d'un modèle d'apprentissage automatique, mais qui ne sont pas appris à partir des données elles-mêmes. Ces paramètres influencent directement la façon dont le modèle s'optimise et converge. 

Le réglage correct de ces hyperparamètres dans AdamW est essentiel pour obtenir une formation efficace, éviter le surajustement et s'assurer que le modèle se généralise bien à des données inédites. 

Dans cette section, nous verrons comment affiner les hyperparamètres clés d'AdamW pour obtenir des performances optimales.

Bonnes pratiques pour le choix des taux d'apprentissage et de la décroissance des poids

Le taux d'apprentissage est un hyperparamètre qui contrôle le degré d'ajustement des poids du modèle par rapport au gradient de perte à chaque étape de l'apprentissage. Un taux d'apprentissage plus élevé accélère la formation mais peut amener le modèle à dépasser les poids optimaux, tandis qu'un taux plus faible permet des ajustements plus fins mais peut ralentir la formation ou rester bloqué dans des minima locaux.

La décroissance du poids, quant à elle, est une technique de régularisation utilisée pour éviter l'ajustement excessif en pénalisant les poids importants dans le modèle. Le Weight decay ajoute une petite pénalité proportionnelle à la taille des poids du modèle pendant l'apprentissage, ce qui permet de réduire la complexité du modèle et d'améliorer la généralisation à de nouvelles données.

Choisir les taux d'apprentissage optimaux et les valeurs de décroissance des poids pour AdamW : 

1. Commencez par un taux d'apprentissage modéré - Pour AdamW, un taux d'apprentissage d'environ 1e-3 est souvent un bon point de départ. Vous pouvez l'ajuster en fonction de la qualité de la convergence du modèle, en l'abaissant si le modèle peine à converger ou en l'augmentant si la formation est trop lente.
2. Expérimentez la décroissance du poids. Commencez par une valeur comprise entre 1e-2 et 1e-4, en fonction de la taille du modèle et de l'ensemble de données. Une décroissance de poids légèrement plus élevée peut aider à prévenir le surajustement pour les modèles complexes et de grande taille, tandis que les modèles plus petits peuvent nécessiter une régularisation moins importante.
3. Utilisez la programmation des taux d'apprentissage. Mettez en œuvre des programmes de taux d'apprentissage (comme la décroissance par paliers ou le recuit en cosinus) pour réduire dynamiquement le taux d'apprentissage au fur et à mesure que l'apprentissage progresse, ce qui aide le modèle à affiner ses paramètres à mesure qu'il s'approche de la convergence.
4. Contrôler les performances. Suivre en permanence les performances du modèle sur l'ensemble de validation. Si vous observez un surajustement, envisagez d'augmenter la décroissance du poids, ou si la perte d'entraînement plafonne, diminuez le taux d'apprentissage pour une meilleure optimisation.

Réflexions finales

AdamW s'est imposé comme l'un des optimiseurs les plus efficaces dans le domaine de l'apprentissage profond, en particulier pour les modèles à grande échelle. Ceci est dû à sa capacité à découpler la décroissance du poids des mises à jour du gradient. En particulier, la conception d'AdamW améliore la régularisation et aide les modèles à mieux se généraliser, notamment lorsqu'il s'agit d'architectures complexes et d'ensembles de données étendus. 

Comme le montre ce tutoriel, la mise en œuvre d'AdamW dans PyTorch est simple - elle nécessite juste quelques ajustements de la part d'Adam. Cependant, le réglage des hyperparamètres reste une étape cruciale pour maximiser l'efficacité d'AdamW. Il est essentiel de trouver le bon équilibre entre le taux d'apprentissage et la décroissance des poids pour garantir que l'optimiseur fonctionne efficacement sans suradapter ou sous-adapter le modèle.

Vous en savez maintenant assez pour mettre en œuvre AdamW dans vos propres modèles. Pour poursuivre votre apprentissage, consultez certaines de ces ressources : 

• Aide-mémoire Keras : Réseaux neuronaux en Python
• La descente de gradient dans l'apprentissage automatique : Une plongée en profondeur
• Guide des certifications et certificats PyTorch
• Apprentissage profond intermédiaire avec PyTorch