Probabilité composée : Définition, règles et exemples

Vous lancez deux dés dans un jeu de société. Quelles sont les chances que vous obteniez un six sur les deux dés ? Ou peut-être analysez-vous les données clients et avez-vous besoin de connaître la probabilité qu'un utilisateur clique sur une publicité ou effectue un achat.

Ces scénarios impliquent une probabilité composée, qui calcule la probabilité que plusieurs événements se produisent, qu'ils surviennent ensemble ou séparément. Si cela vous semble confus, ne vous inquiétez pas : Je vais illustrer ces concepts à l'aide d'exemples clairs afin de faciliter leur compréhension.

Qu'est-ce que la probabilité composée ?

La probabilité composée évalue la probabilité lorsque deux événements ou plus sont impliqués. La probabilité simple se concentre sur un événement unique (comme le lancer d'une pièce), tandis que la probabilité composée traite des situations où plusieurs événements peuvent se produire.

En statistiques formelles, ces scénarios ont des noms spécifiques : le scénario ET est la probabilité conjointe (la probabilité que les deux événements se produisent ensemble), et le scénario OU est l'union (la probabilité qu'au moins un événement se produise).

Considérez la probabilité composée comme un terme générique accessible aux débutants qui vous aide à apprendre les deux types de calculs avant de vous plonger dans ces termes plus techniques.

Types d'événements probabilistes composés

La distinction AND/OR vous indique quelle formule utiliser, mais il existe une autre relation entre les événements qui modifie le fonctionnement de ces formules. Avant de pouvoir calculer avec précision des probabilités composées, il est nécessaire de comprendre comment les événements sont liés les uns aux autres. Plus précisément, si un événement influence l'autre.

Événements indépendants

Deux événements sont indépendants lorsqu'aucun des deux n'influence l'autre. Veuillez lancer une pièce, puis un dé. Obtenir des têtes ne modifie en rien vos chances d'obtenir un quatre. Chaque événement possède sa propre probabilité qui reste constante.

Parmi les exemples classiques, on peut citer le fait de lancer plusieurs dés, de lancer plusieurs pièces de monnaie ou de tirer des cartes avec remplacement (en remettant chaque carte en place avant le prochain tirage). En science des données, l'indépendance est observée lors de l'analyse de sessions utilisateur distinctes ou de groupes de tests A/B non liés.

Événements dépendants

Les événements sont dépendants lorsque le premier événement modifie la probabilité du second. Veuillez tirer une carte d'un jeu, puis en tirer une autre sans remettre la première. Le deuxième tirage présente des cotes différentes, car la composition du jeu a changé.

Vous observerez des événements dépendants lors d'un échantillonnage sans remplacement, dans des processus décisionnels séquentiels ou lorsque les événements sont liés de manière causale. La probabilité d'un deuxième achat dépend du fait que le client ait effectué un premier achat. Cette dépendance a une incidence directe sur vos calculs.

Règles pour le calcul de la probabilité composée

Maintenant que vous comprenez les relations entre les événements, nous pouvons aborder les calculs proprement dits.

L'indépendance ou la dépendance dont vous venez d'apprendre la définition détermine directement la version de la formule que vous utiliserez. La méthode de calcul dépend du type de scénario (AND ou OR) et, dans ces scénarios, du caractère indépendant ou dépendant de vos événements.

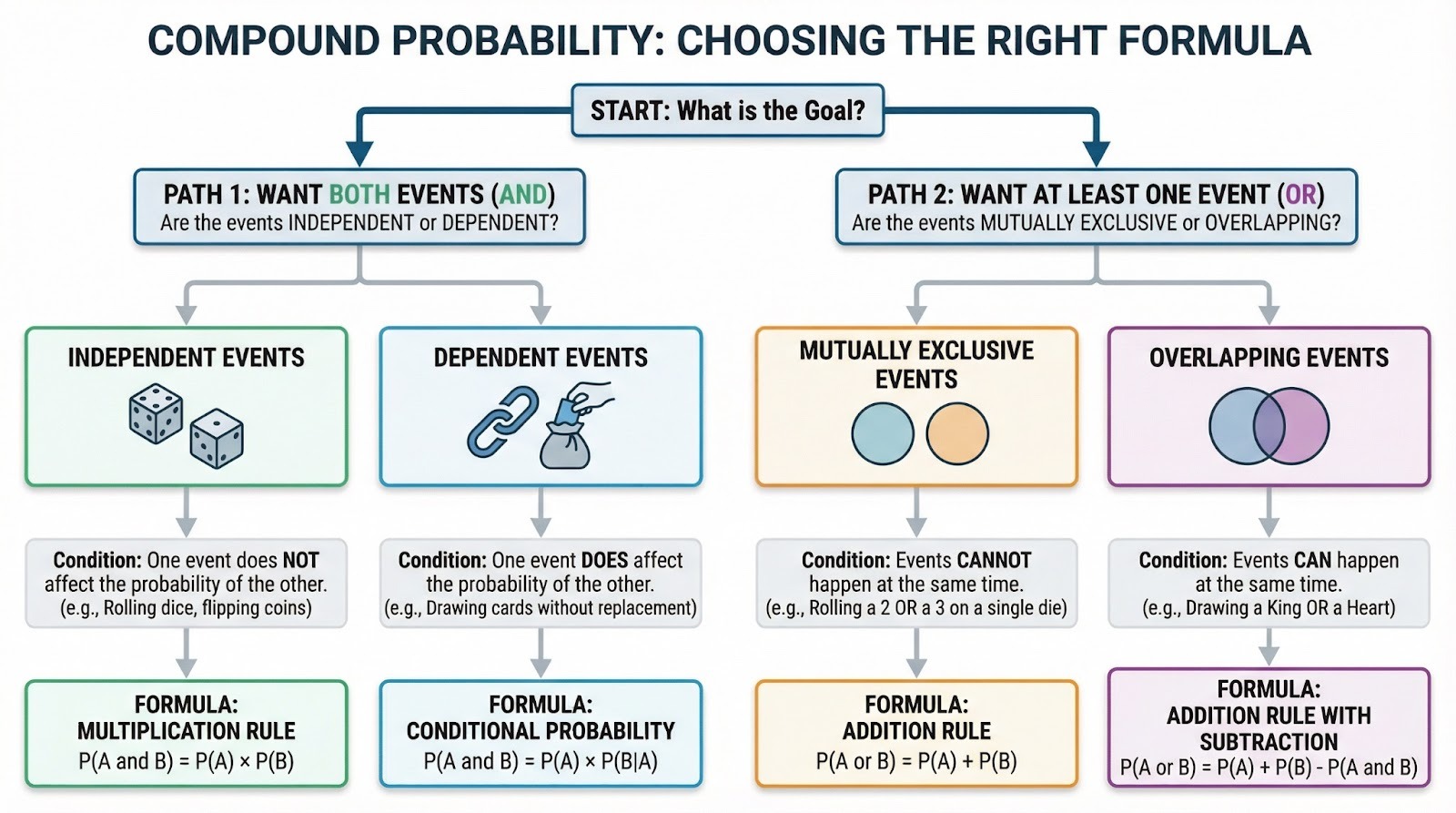
Organigramme décisionnel pour choisir la formule de probabilité composée appropriée. Image fournie par l'auteur.

La règle de multiplication

La règle de multiplication traite les scénarios ET (lorsque vous souhaitez que les deux événements se produisent). Pour les événements indépendants, il convient de multiplier leurs probabilités individuelles : P(A ∩ B) = P(A) × P(B). Obtenir un quatre ET obtenir pile ? Cela correspond à (1/6) × (1/2) = 1/12.

Pour les événements dépendants, il est nécessaire d'utiliser la probabilité conditionnelle : P(A ∩ B) = P(A) × P(B|A). Cela signifie « la probabilité de A multipliée par la probabilité de B, étant donné que A s'est produit ». Tirer deux as sans remplacement ? Le premier as est 4/52, mais le deuxième as est désormais 3/51, car vous piochez dans un jeu plus petit. Veuillez les multiplier : (4/52) × (3/51) = 1/221.

Règle d'addition (lorsque les événements se chevauchent)

La règle d'addition traite les scénarios OU (lorsque vous souhaitez qu'au moins un événement se produise). Si les événements ne peuvent pas se produire simultanément (mutuellement exclusifs), veuillez simplement ajouter : P(A ou B) = P(A) + P(B). Obtenir un deux OU un trois avec un dé signifie 1/6 + 1/6 = 1/3.

Lorsque des événements peuvent se chevaucher, il est nécessaire de soustraire l'intersection afin d'éviter tout double comptage : P(A ou B) = P(A) + P(B) - P(A ∩ B). Tirer un roi OU un cœur d'un jeu de cartes ? Il y a 4 rois et 13 cœurs, mais le roi de cœur est compté deux fois, donc : 4/52 + 13/52 - 1/52 = 16/52.

Exemples étape par étape de probabilité composée

Examinons des exemples concrets pour comprendre comment ces règles s'appliquent. La probabilité composée est un terme générique qui englobe à la fois les scénarios d'événements indépendants et dépendants.

Exemple avec des événements indépendants

Vous lancez une pièce équitable deux fois. Quelle est la probabilité d'obtenir pile les deux fois ? Étant donné que les lancers de pièce sont indépendants, chaque lancer a une probabilité de 1/2. En utilisant la règle de multiplication : P(Pile au lancer 1 ET Pile au lancer 2) = 1/2 × 1/2 = 1/4. Il y a 25 % de chances d'obtenir deux faces consécutives.

Exemple avec des événements dépendants

Un sac contient 5 billes bleues et 3 billes rouges. Veuillez tirer deux billes sans les remettre dans le sac. Quelle est la probabilité que les deux soient bleus ? Le premier tirage a une probabilité de 5/8. Après avoir retiré une bille bleue, il ne reste plus que 4 billes bleues dans un sac qui en contient 7, donc P(Bleu au deuxième tirage | Bleu au premier) = 4/7. Par conséquent : P(Les deux bleus) = 5/8 × 4/7 = 20/56 = 5/14, soit environ 35,7 %.

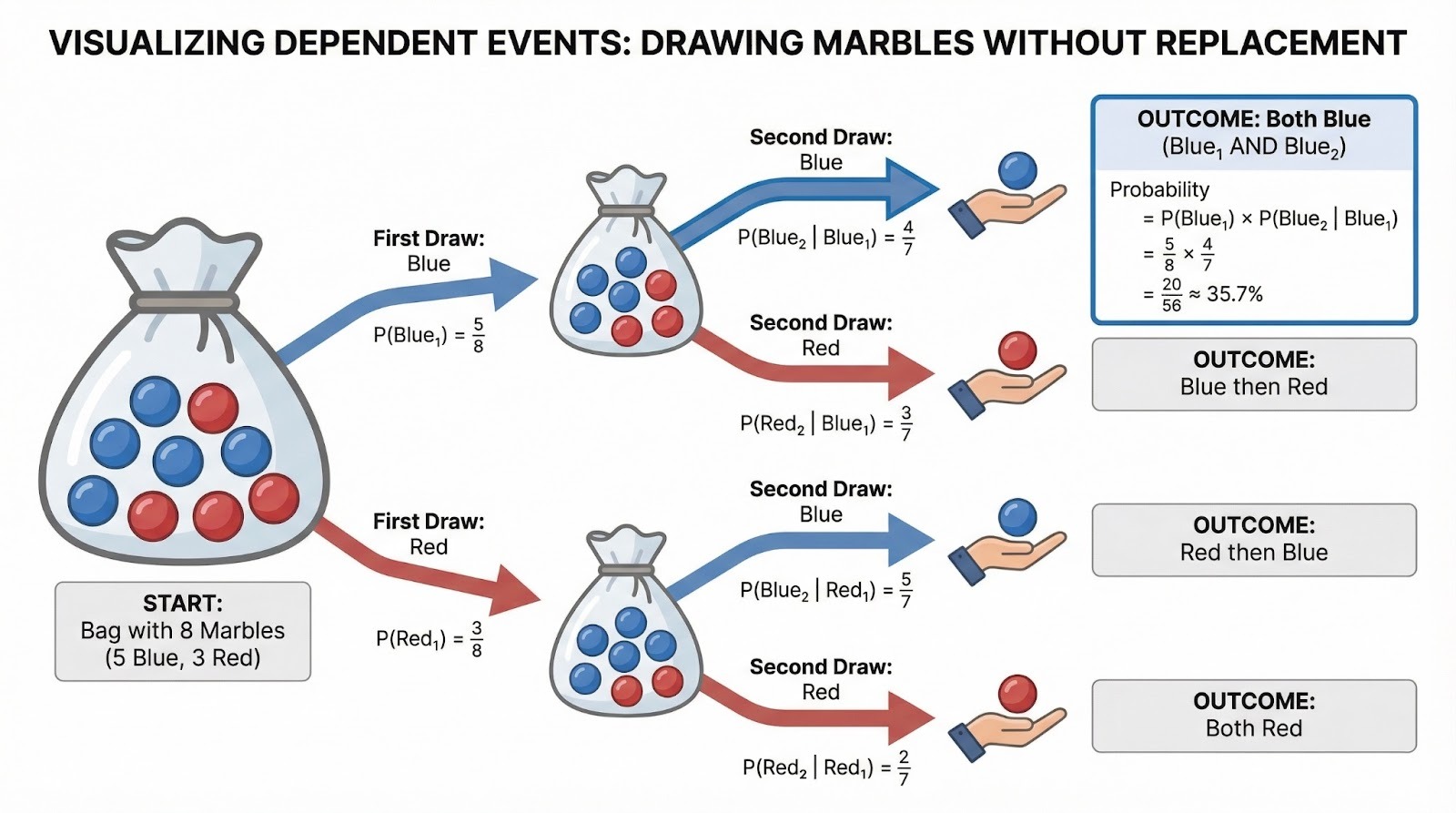
Diagramme arborescent illustrant les événements dépendants lors du tirage de billes sans remplacement. Image fournie par l'auteur.

Exemple impliquant « AND » et « OR »

Il est important de lire attentivement ce qui suit. Un dé standard est lancé. Quelle est la probabilité d'obtenir un nombre inférieur à 3 OU un nombre pair ? Nombres inférieurs à 3 : {1, 2}. Nombres pairs : {2, 4, 6}. Ces éléments se chevauchent à 2, nous ne pouvons donc pas simplement les additionner. En utilisant la règle d'addition : P(moins de 3) = 2/6, P(pair) = 3/6, P(les deux) = 1/6. Par conséquent : 2/6 + 3/6 - 1/6 = 4/6 = 2/3.

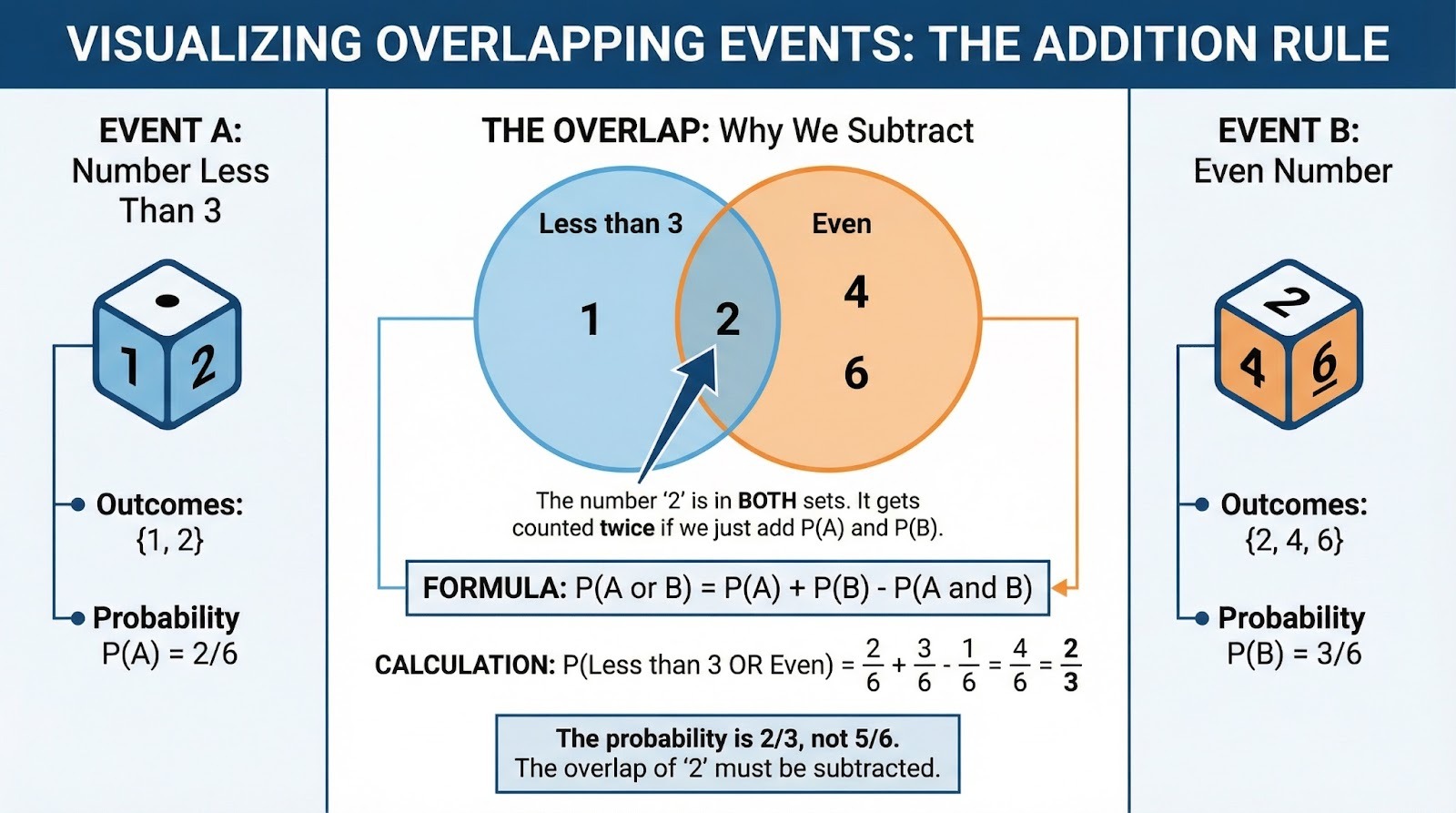
Diagramme de Venn illustrant des événements qui se chevauchent. Image fournie par l'auteur.

Veuillez noter que le mot « ou » indique que nous avons besoin d'une addition, tandis que « et » indiquerait une multiplication. Le langage utilisé dans les questions de probabilité vous indique quelle règle appliquer.

Erreurs de probabilité composée

Considérer des événements dépendants comme indépendants constitue l'erreur la plus fréquente. Si vous tirez des cartes sans les remplacer mais multipliez les probabilités comme si le jeu ne changeait pas, votre réponse sera incorrecte. Veuillez toujours vous demander : le premier événement modifie-t-il les conditions du second ?

L'addition de probabilités lorsqu'une multiplication est nécessaire se produit lorsque les gens interprètent à tort « et » comme « ou ». Si une question demande la probabilité que l'événement A ET l'événement B se produisent, il convient de multiplier (en supposant l'indépendance ou en utilisant la probabilité conditionnelle). L'ajout vous offre un scénario complètement différent.

Une mauvaise interprétation de « et » par rapport à « ou » peut entraîner une certaine confusion, car le langage courant est moins précis que le langage mathématique. « Quelles sont les chances qu'il pleuve ou qu'il neige demain ? » signifie au moins l'une des deux, pas les deux (c'est une addition). « Quelles sont les chances qu'il pleuve et qu'il neige demain ? » signifie que les deux phénomènes se produisent (il s'agit d'une multiplication).

Oublier d'ajuster les probabilités après qu'un résultat se soit produit apparaît dans les scénarios séquentiels. Après avoir tiré une carte, le jeu contient 51 cartes, et non 52. Lorsqu'un client quitte l'établissement, votre échantillon diminue d'une unité. Veuillez mettre à jour vos probabilités à chaque étape.

Comment se manifeste la probabilité composée

Dans les jeux de hasard, les casinos utilisent la probabilité composée pour calculer l'avantage de la maison. Comprendre la probabilité de plusieurs résultats favorables aide les joueurs à prendre des décisions de pari éclairées (même si la maison dispose toujours d'un avantage mathématique intégré). L'analyse des risques dans le domaine des affaires et de la finance repose largement sur la probabilité composée. Quelle est la probabilité d'un ralentissement du marché ET d'une hausse des taux d'intérêt ? Ces scénarios composés aident les entreprises à se prémunir contre plusieurs facteurs de risque pouvant survenir simultanément.

Les processus de contrôle qualité utilisent la probabilité composée pour évaluer la probabilité de défauts. Si deux étapes de fabrication présentent chacune un taux de défauts de 2 %, la probabilité composée vous indique le taux de défauts global pour les produits passant par les deux étapes. Les tests médicaux combinent plusieurs résultats de tests à l'aide de la probabilité composée. Un patient peut subir plusieurs tests diagnostiques, et les médecins doivent connaître la probabilité de la maladie en tenant compte de l'ensemble des résultats des tests, et non d'un seul test pris isolément.

Notre cours « Fondements de la probabilité en Python » traiteen profondeur des applications pratiques telles quecelles-ci.

Probabilité composée par rapport à Probabilité conditionnelle

La probabilité conditionnelle pose la question suivante : Étant donné que B s'est produit, quelle est la probabilité que A se produise ? Vous êtes en train de mettre à jour votre estimation de probabilité suren fonction de nouvelles informations. La probabilité composée pose la question suivante : Quelle est la probabilité que plusieurs événements se produisent dans une certaine combinaison ?

Ils sont liés lors du calcul de la probabilité composée pour des événements dépendants. Vous utilisez la probabilité conditionnelle dans votre règle de multiplication. P(A ∩ B) = P(A) × P(B|A) illustre clairement cette relation. La probabilité conditionnelle P(B|A) vous aide à calculer la probabilité combinée de A et B.

Considérez cela de cette manière. La probabilité conditionnelle est un outil utilisé dans les calculs de probabilité composée. Lorsque des événements sont dépendants, il n'est pas possible de calculer des probabilités composées sans tenir compte de la manière dont un événement en influence un autre, et c'est précisément ce que mesure la probabilité conditionnelle.

Conseils pratiques pour résoudre des problèmes de probabilité composée

Commencez par déterminer le nombre d'événements concernés et s'ils sont indépendants ou dépendants. Recherchez des indices : le problème mentionne-t-il un remplacement ? Un événement modifie-t-il les conditions du suivant ? Les événements indépendants conservent des probabilités constantes, tandis que les événements dépendants nécessitent une mise à jour des probabilités après chaque événement.

Traduisez « et » ou « ou » avec soin, car ces mots déterminent l'ensemble de votre approche. Veuillez noter ce que vous savez avant de procéder au calcul. Veuillez énumérer les probabilités individuelles, identifier les probabilités conditionnelles et esquisser un diagramme rapide si vous travaillez avec des événements séquentiels. Ce travail préparatoire permet d'éviter les erreurs lorsque vous commencez à calculer.

Veuillez vérifier que vos résultats sont raisonnables. Les probabilités doivent être comprises entre 0 et 1. Si vous multipliez des probabilités, votre réponse devrait être inférieure à la plus petite probabilité individuelle. Si quelque chose vous semble incorrect, veuillez vérifier votre travail avant de passer à l'e section. Notre cours « Probability Puzzles in R » (Casse-têtes probabilistes dans R) propose des exercices pratiques sur ces stratégies de résolution de problèmes.

Conclusion

La probabilité composée fournit le cadre mathématique permettant de traiter plusieurs événements combinés. La clé consiste à déterminer si vous avez affaire à des scénarios ET (règle de multiplication) ou à des scénarios OU (règle d'addition), et si vos événements sont indépendants ou dépendants. Ces distinctions déterminent la formule que vous utiliserez.

Avec de la pratique, vous développerez votre intuition pour ces problèmes. Les applications concrètes en science des données (des tests A/B à la modélisation des risques) utilisent ces mêmes principes. Commencez par des exemples simples, suivez la logique étape par étape et renforcez votre confiance en vous avec des scénarios de plus en plus complexes.