Compound Probability: Definition, Rules, and Examples

You're rolling two dice in a board game. What are the chances you'll roll a six on both? Or maybe you're analyzing customer data and need to know the probability that a user either clicks an ad or makes a purchase.

These scenarios involve compound probability, which calculates the likelihood of multiple events, whether they happen together or separately. If it sounds confusing, don't worry: I’ll make the ideas easy to follow with clear examples.

What Is Compound Probability?

Compound probability calculates the likelihood when two or more events are involved. Simple probability focuses on a single event (like flipping one coin), but compound probability handles situations where multiple things can happen.

In formal statistics, these scenarios have specific names: the AND scenario is joint probability (the probability of both events occurring together), and the OR scenario is the union (the probability of at least one event occurring).

Think of compound probability as the beginner-friendly umbrella term that helps you learn both types of calculations before diving into these more technical terms.

Types of Compound Probability Events

The AND/OR distinction tells you which formula to use, but there's another relationship between events that changes how those formulas work. Before you can calculate compound probabilities accurately, you need to understand how events relate to each other. Specifically, whether one event influences the other.

Independent events

Two events are independent when one doesn't affect the other. Flip a coin, then roll a die. Getting heads doesn't change your chances of rolling a four. Each event has its own probability that stays constant.

Classic examples include rolling multiple dice, flipping several coins, or drawing cards with replacement (putting each card back before the next draw). In data science, you'll see independence when analyzing separate user sessions or unrelated A/B test groups.

Dependent events

Events are dependent when the first event changes the probability of the second. Draw a card from a deck, then draw another without putting the first back. The second draw has different odds because the deck's composition changed.

You'll see dependent events when sampling without replacement, in sequential decision processes, or when events are causally linked. The probability of a second purchase depends on whether the customer made a first purchase. This dependency directly affects your calculations.

Rules for Calculating Compound Probability

Now that you understand event relationships, we can tackle the actual calculations.

The independence or dependence you just learned about directly determines which version of the formula you'll use. The calculation method depends on whether you're dealing with AND or OR scenarios, and within those scenarios, whether your events are independent or dependent.

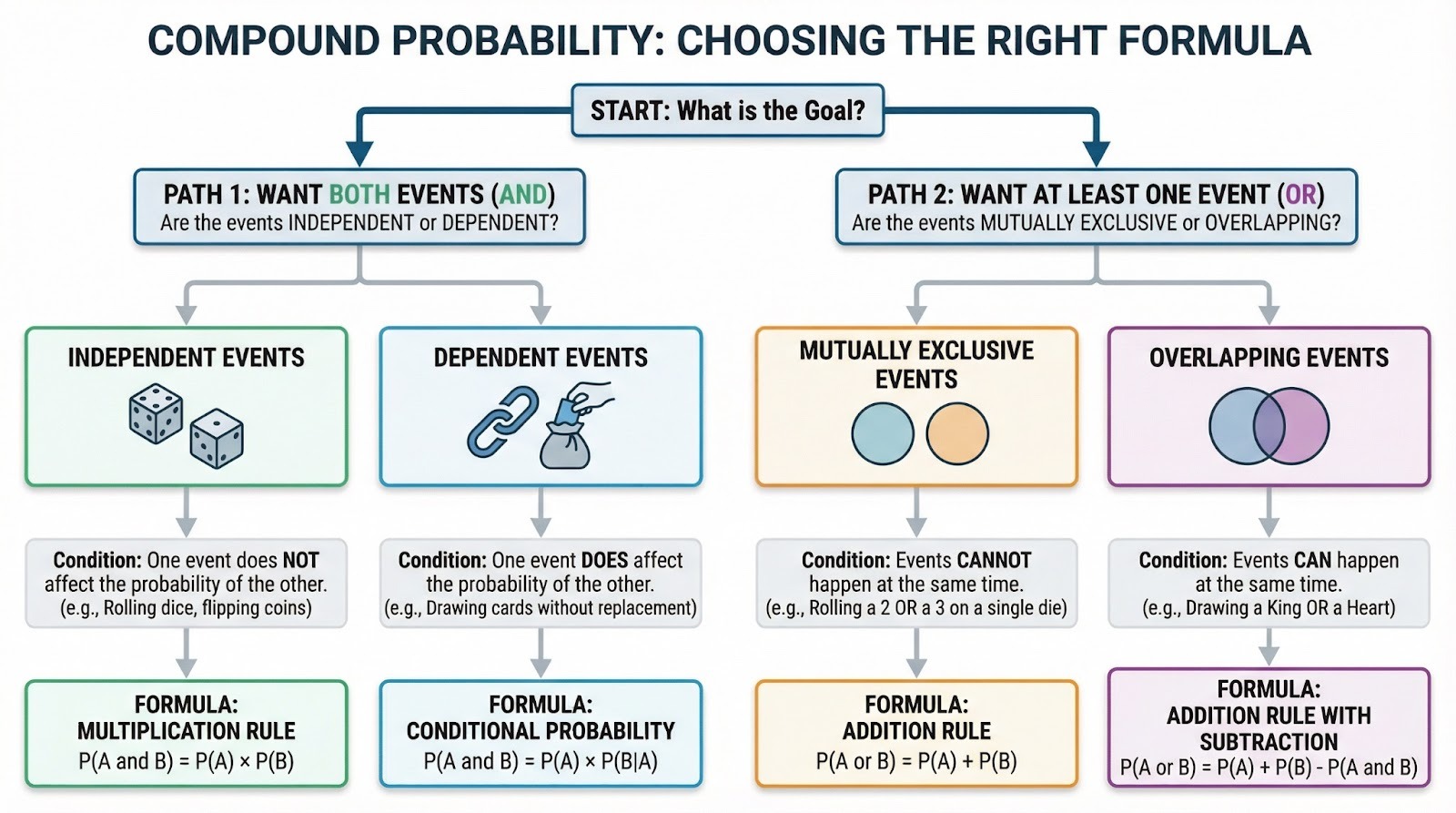
Decision flowchart for choosing the correct compound probability formula. Image by Author.

The multiplication rule

The multiplication rule handles AND scenarios (when you want both events to occur). For independent events, multiply their individual probabilities: P(A ∩ B) = P(A) × P(B). Rolling a four AND flipping heads? That's (1/6) × (1/2) = 1/12.

For dependent events, you'll need conditional probability: P(A ∩ B) = P(A) × P(B|A). This means "the probability of A times the probability of B given that A happened." Drawing two aces without replacement? First ace is 4/52, but the second ace is now 3/51 because you're drawing from a smaller deck. Multiply them: (4/52) × (3/51) = 1/221.

The addition rule (when events overlap)

The addition rule handles OR scenarios (when you want at least one event to occur). If events can't happen simultaneously (mutually exclusive), just add: P(A or B) = P(A) + P(B). Rolling a two OR a three on one die means 1/6 + 1/6 = 1/3.

When events can overlap, you need to subtract the intersection to avoid double-counting: P(A or B) = P(A) + P(B) - P(A ∩ B). Drawing a king OR a heart from a deck? There are 4 kings and 13 hearts, but the king of hearts gets counted twice, so: 4/52 + 13/52 - 1/52 = 16/52.

Step-by-Step Examples of Compound Probability

Let's work through concrete examples to see how these rules apply. Compound probability is an umbrella term that covers both independent and dependent event scenarios.

Example with independent events

You flip a fair coin twice. What's the probability of getting heads both times? Since coin flips are independent, each flip has probability 1/2. Using the multiplication rule: P(Heads on flip 1 AND Heads on flip 2) = 1/2 × 1/2 = 1/4. There's a 25% chance of getting two heads in a row.

Example with dependent events

A bag contains 5 blue marbles and 3 red marbles. You draw two marbles without replacement. What's the probability both are blue? The first draw has probability 5/8. After removing one blue marble, only 4 blue marbles remain in a bag of 7, so P(Blue on second draw | Blue on first) = 4/7. Therefore: P(Both blue) = 5/8 × 4/7 = 20/56 = 5/14, approximately 35.7%.

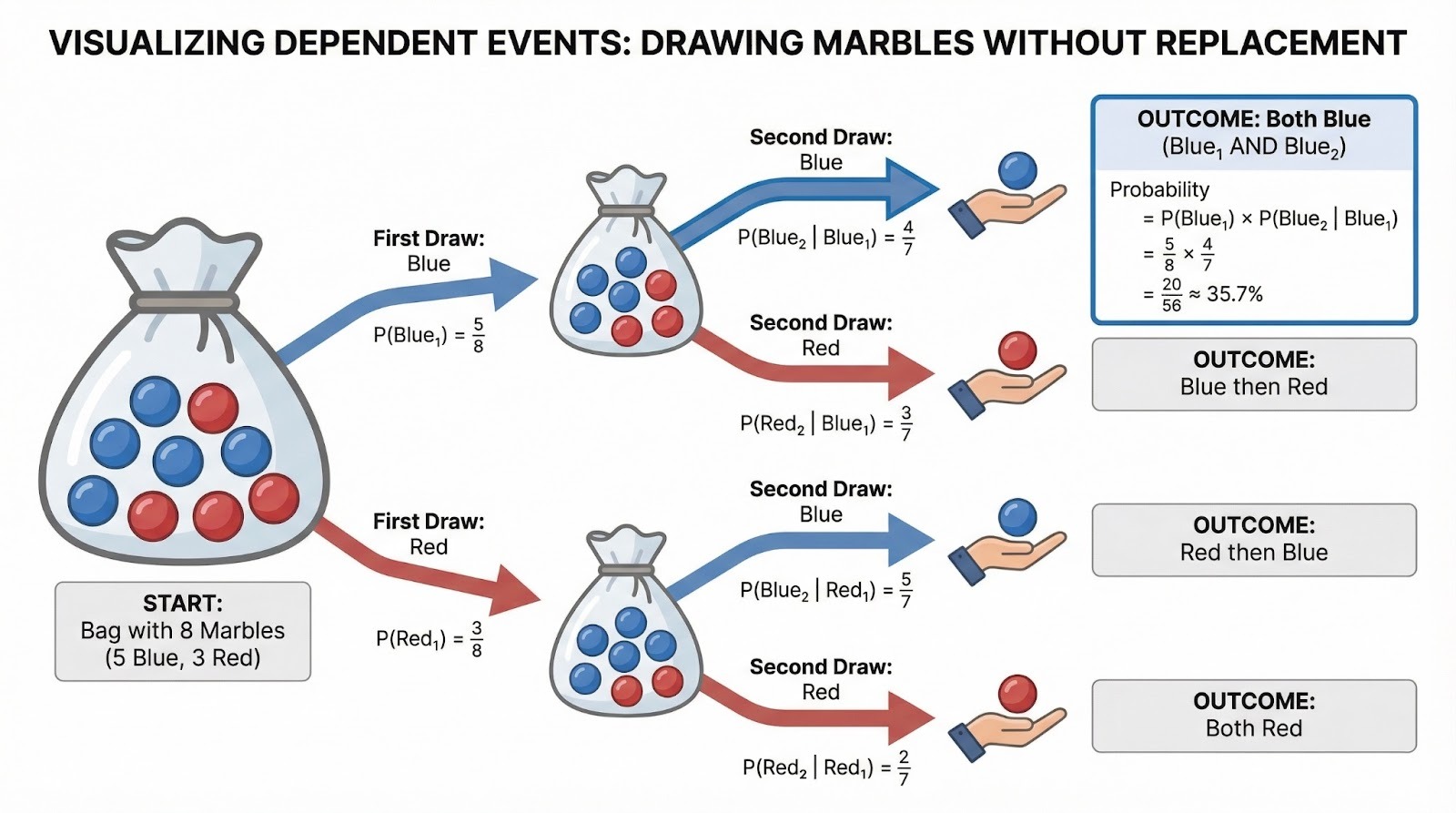
Tree diagram visualizing dependent events when drawing marbles without replacement. Image by Author.

Example involving "AND" vs "OR"

Careful reading matters here. A standard die is rolled. What's the probability of rolling a number less than 3 OR an even number? Numbers less than 3: {1, 2}. Even numbers: {2, 4, 6}. These overlap at 2, so we can't just add. Using the addition rule: P(Less than 3) = 2/6, P(Even) = 3/6, P(Both) = 1/6. Therefore: 2/6 + 3/6 - 1/6 = 4/6 = 2/3.

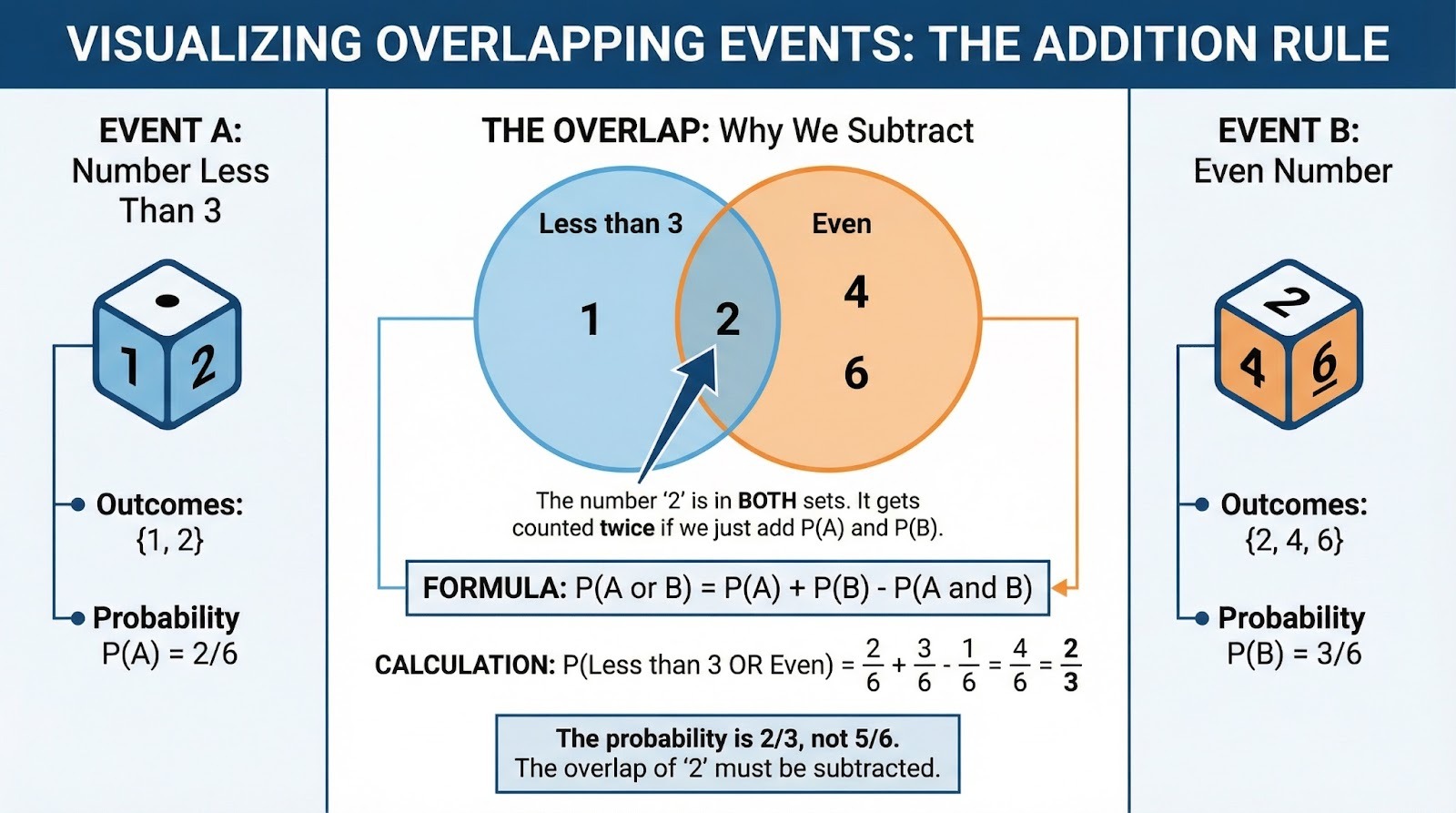
Venn diagram showing overlapping events. Image by Author.

Notice how the word "or" signals we need addition, while "and" would signal multiplication. The language in probability questions tells you which rule to apply.

Compound Probability Mistakes

Treating dependent events as independent is the most frequent mistake. If you draw cards without replacement but multiply probabilities as if the deck doesn't change, your answer will be wrong. Always ask: does the first event change the conditions for the second?

Adding probabilities when multiplication is required happens when people misinterpret "and" as "or." If a question asks for the probability of event A AND event B, you multiply (assuming independence or using conditional probability). Adding gives you a completely different scenario.

Misinterpreting "and" versus "or" causes confusion because everyday language is less precise than mathematical language. "What are the chances of rain or snow tomorrow?" means at least one, not both (that's addition). "What are the chances of rain and snow tomorrow?" means both occurring (that's multiplication).

Forgetting to adjust probabilities after an outcome occurs shows up in sequential scenarios. After drawing one card, the deck has 51 cards, not 52. After one customer leaves, you have one fewer in your sample. Update your probabilities at each step.

How Compound Probability Shows Up

In games of chance, casinos use compound probability to calculate house edge. Understanding the probability of multiple favorable outcomes helps players make informed betting decisions (though the house always has its mathematical advantage built in). Risk analysis in business and finance relies heavily on compound probability. What's the probability of both a market downturn AND rising interest rates? These compound scenarios help companies hedge against multiple risk factors occurring simultaneously.

Quality control processes use compound probability to assess the likelihood of defects. If two manufacturing stages each have a 2% defect rate, compound probability tells you the overall defect rate for products passing through both stages. Medical testing combines multiple test results using compound probability. A patient might receive several diagnostic tests, and doctors need to know the probability of disease given all test results together, not just one test in isolation.

Our Foundations of Probability in Python course covers practical applications like these in depth.

Compound Probability vs. Conditional Probability

Conditional probability asks: "Given that B happened, what's the probability of A?" You're updating your probability estimate based on new information. Compound probability asks: "What's the probability that multiple events occur in some combination?"

They connect when calculating compound probability for dependent events. You use conditional probability in your multiplication rule. P(A ∩ B) = P(A) × P(B|A) shows this relationship explicitly. The conditional probability P(B|A) helps you calculate the compound probability of both A and B.

Think of it this way. Conditional probability is a tool you use within compound probability calculations. When events are dependent, you can't calculate compound probabilities without considering how one event affects another, and that's exactly what conditional probability measures.

Practice Tips for Solving Compound Probability Problems

Start by identifying how many events are involved and whether they're independent or dependent. Look for clues: does the problem mention replacement? Does one event change the conditions for the next? Independent events keep their probabilities constant, while dependent events require you to update probabilities after each event.

Translate "and" or "or" carefully because these words determine your entire approach. Write down what you know before calculating. List out the individual probabilities, identify any conditional probabilities, and sketch a quick diagram if you're working with sequential events. This prep work prevents mistakes when you start calculating.

Check your results for basic reasonableness. Probabilities must be between 0 and 1. If you're multiplying probabilities, your answer should be smaller than the smallest individual probability. If something seems off, review your work before moving forward. Our Probability Puzzles in R course offers practice with these problem-solving strategies.

Conclusion

Compound probability gives you the mathematical framework to handle multiple events in combination. The key is recognizing whether you're dealing with AND scenarios (multiplication rule) or OR scenarios (addition rule), and whether your events are independent or dependent. These distinctions determine which formula you'll use.

With practice, you'll develop intuition for these problems. Real-world applications in data science (from A/B testing to risk modeling) use these same principles. Start with simple examples, work through the logic step by step, and build your confidence with increasingly complex scenarios.