Probabilité conditionnelle : Un examen approfondi

Imaginez que vous développiez un système de détection de spam pour le courrier électronique. Dans un premier temps, vous pouvez signaler un courriel comme suspect s'il contient certains mots-clés. Mais que se passe-t-il si vous découvrez que cet e-mail provient d'un expéditeur de confiance ? Ou si elle a été envoyée à une heure inhabituelle ? Chaque nouvelle information modifie la probabilité que l'e-mail soit un spam. Cette mise à jour dynamique des probabilités sur la base de nouvelles preuves est au cœur de la probabilité conditionnelle, un concept qui alimente de nombreuses applications modernes de la science des données, du filtrage des courriers électroniques à la détection des fraudes. 

Pour ceux qui débutent dans les concepts de probabilités, l'Aide-mémoire sur l'introduction aux règles de probabilités constitue une référence utile pour les principes et les formules de base. Le cours d'introduction aux statistiques construit une base solide en explorant les distributions de probabilité et leurs propriétés, qui constituent la base de la compréhension du fonctionnement des probabilités conditionnelles dans la pratique. Ces ressources offrent une voie structurée pour développer des bases solides dans les concepts que nous allons explorer dans cet article.

Qu'est-ce que la probabilité conditionnelle ?

La probabilité conditionnelle mesure la probabilité qu'un événement se produise lorsque l'on sait qu'un autre événement a déjà eu lieu. Lorsque nous recevons de nouvelles informations sur un événement, nous ajustons nos calculs de probabilité en conséquence.

Pour comprendre ce concept, prenons un exemple avec des cartes à jouer. Lorsque vous tirez une carte d'un jeu standard, il y a 52 résultats possibles. Si vous voulez tirer un roi, votre probabilité initiale est de 4/52 (environ 7,7 %) puisqu'il y a quatre rois dans le jeu. Mais que se passe-t-il si quelqu'un vous dit que la carte que vous avez tirée est une carte cachée ? Cette nouvelle information change tout - votre probabilité d'avoir un roi est maintenant beaucoup plus élevée, à 4/12 (environ 33,3 %), puisqu'il n'y a que douze cartes faces au total.

Cette relation entre les probabilités a une définition mathématique précise :

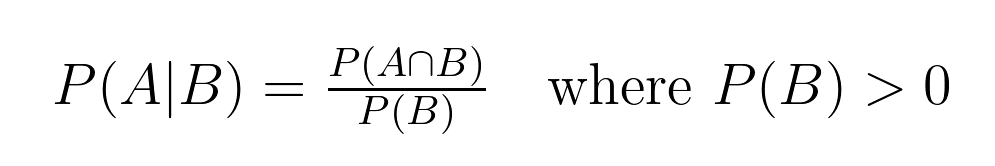
Cette formule nous aide à calculer la probabilité conditionnelle, où :

• P(A|B) représente la probabilité que l'événement A se produise, étant donné que l'événement B s'est produit. Cela se lit comme "la probabilité de A étant donné B".
• P(A∩B) représente la probabilité conjointe, ou la probabilité que les événements A et B se produisent ensemble. Il s'agit de la "probabilité que l'intersection de A et de B se produise".
• P(B) représente la probabilité que l'événement B se produise.

Dans notre exemple de carte :

• L'événement A est "tirer un roi"
• L'événement B est le "tirage d'une carte"
• P(A|B) = 4/12 (probabilité d'obtenir un roi, étant donné que nous avons une carte de face)
• P(A∩B) = 4/52 (probabilité de tirer un roi, qui est toujours une carte cachée)
• P(B) = 12/52 (probabilité de tirer une carte face)

Pour mieux comprendre le fonctionnement pratique des probabilités conditionnelles, nous pouvons utiliser un diagramme en arbre. Les diagrammes en arbre sont particulièrement utiles car ils montrent comment chaque nouvelle information modifie nos probabilités :

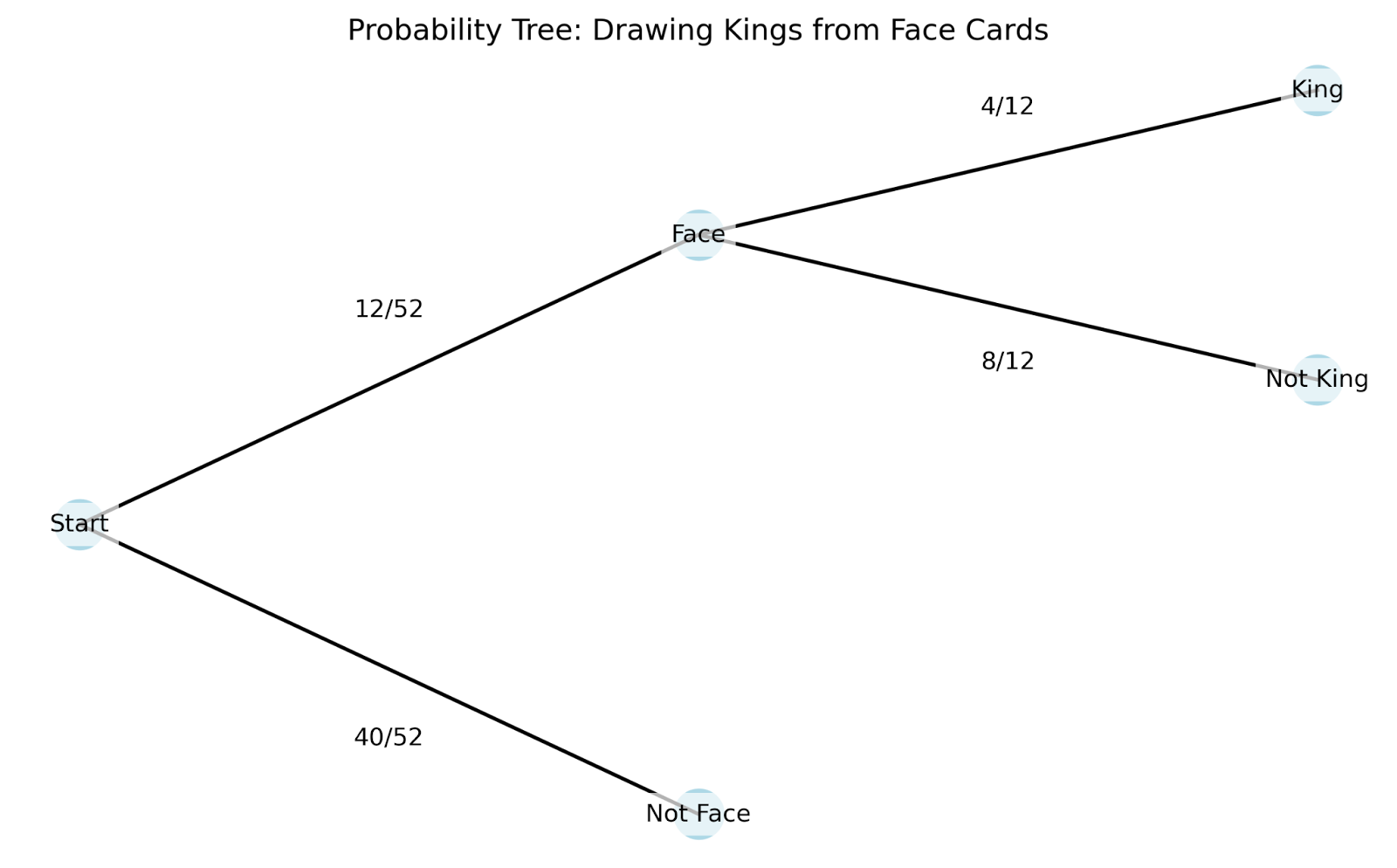
Voyons comment fonctionne ce diagramme en arbre :

1. Nous commençons à la racine (point le plus à gauche) avec les 52 cartes.
2. Les premières branches indiquent notre premier élément d'information - s'agit-il d'une carte de face ou non ?
3. Si nous suivons la branche de la carte visible, elle se divise à nouveau en fonction de notre deuxième information - s'agit-il d'un roi ?

Le diagramme en arbre nous aide à comprendre plusieurs concepts clés de la probabilité conditionnelle :

• Espace d'échantillonnage : Il s'agit de tous les résultats possibles dans notre scénario. L'espace d'échantillonnage initial est de 52 cartes, mais il est "réduit" à 12 cartes une fois que nous savons que nous avons une carte de face.
• Événements : Il s'agit de résultats spécifiques qui nous intéressent, comme "tirer une carte" ou "tirer un roi". Les branches de notre arbre représentent différents événements.
• Probabilité conjointe : Il s'agit de la probabilité que plusieurs événements se produisent ensemble. Dans notre arbre, nous pouvons trouver cela en multipliant les probabilités le long d'un chemin. Par exemple, la probabilité de tirer un roi ET qu'il s'agisse d'une face est de (12/52) × (4/12) = 4/52.
• Probabilité marginale (inconditionnelle) : Il s'agit de la probabilité qu'un événement se produise sans tenir compte d'autres informations. Dans notre exemple, cela correspond à la probabilité initiale de 4/52 de tirer un roi avant de connaître quoi que ce soit d'autre sur la carte.

L'intérêt de la probabilité conditionnelle est qu'elle nous permet d'actualiser nos probabilités au fur et à mesure que nous obtenons de nouvelles informations. Tout comme nous avons ajusté notre probabilité d'avoir un roi de 7,7 % à 33,3 % lorsque nous avons appris que nous avions une carte visible, la probabilité conditionnelle nous donne un moyen formel de recalculer les probabilités sur la base de nouveaux éléments.

La formule de la probabilité conditionnelle

La structure mathématique de la probabilité conditionnelle nous fournit des outils pour analyser des scénarios complexes impliquant plusieurs événements. Examinons les principales propriétés.

Propriétés clés de la probabilité conditionnelle

Ces propriétés mathématiques nous aident à résoudre des problèmes complexes de manière plus efficace :

1. Propriété de l'indépendance

Lorsque deux événements A et B sont indépendants, nous savons que l'occurrence de l'un n'affecte pas la probabilité de l'autre. Mathématiquement, c'est le cas : P(A|B) = P(A), ce qui signifie : "la probabilité de A étant donné B est égale à la probabilité de A".

Par exemple, si nous lançons un dé et que nous tirons à pile ou face, le fait d'obtenir face ne change pas la probabilité d'obtenir un six. La formule nous l'indique : P(Six|Têtes) = P(Six) = 1/6

2. Règle du complément

Pour tout événement A étant donné une condition B, la somme des probabilités de A et de son complément A' (lire "A premier") doit être égale à 1. Mathématiquement, c'est le cas : P(A|B) + P(A'|B) = 1, ce qui se lit comme suit : "La probabilité de A étant donné B plus la probabilité du complément de A étant donné B est égale à 1.

Dans notre exemple de carte précédent : P(Roi|Carte à face) + P(Pas Roi|Carte à face) = 4/12 + 8/12 = 1

La règle de multiplication et la règle de la chaîne

La règle de multiplication relie les probabilités conjointes aux probabilités conditionnelles : P(A ∩ B) = P(A|B) × P(B). Nous disons : "La probabilité d'une intersection A-B est égale à la probabilité d'une intersection A-B multipliée par la probabilité d'une intersection B".

Cette règle s'étend à plusieurs événements par le biais de la règle de la chaîne. Pour trois événements A, B et C : P(A ∩ B ∩ C) = P(A|B ∩ C) × P(B|C) × P(C). En d'autres termes, "La probabilité de l'intersection A - B - C est égale à la probabilité de l'intersection A - B - C multipliée par la probabilité de l'intersection B - C multipliée par la probabilité de l'intersection C".

Voyons cela en action avec une séquence de tirage de cartes :

1. Tirer un roi (K)
2. A partir des cartes restantes, tirer une reine (Q)
3. Parmi les cartes restantes, tirer un as (A)

P(K ∩ Q ∩ A) = P(A|K ∩ Q) × P(Q|K) × P(K) = (4/50) × (4/51) × (4/52)

La règle de la chaîne est particulièrement utile dans l'apprentissage automatique, notamment dans les réseaux bayésiens où nous devons modéliser des dépendances complexes entre plusieurs variables. Lorsque nous analysons des données, nous rencontrons souvent des situations où les événements suivent une séquence naturelle, et la règle de la chaîne nous aide à décomposer ces scénarios complexes en calculs plus simples et plus faciles à gérer.

Exemples illustrant la probabilité conditionnelle

Passons en revue deux des exemples les plus courants et réfléchissons également à la manière dont les probabilités conditionnelles peuvent apparaître dans votre travail.

Exemples classiques

Ces deux exemples sont très courants et méritent d'être étudiés, surtout si vous passez un entretien :

Jets de dés : Comprendre les espaces d'échantillonnage réduits

Lorsque nous lançons un dé, notre espace d'échantillonnage commence par six possibilités : {1, 2, 3, 4, 5, 6}. Le fait d'apprendre des informations partielles sur le lancer modifie nos calculs de probabilité d'une manière spécifique. Voyons comment :

Probabilité initiale d'obtenir un 6 : P(6) = 1/6

Si nous apprenons que le résultat est pair, notre espace d'échantillonnage se réduit à {2, 4, 6} : P(6 | pair) = 1/3

Les billes : Dépendances séquentielles

Un sac contient 5 billes bleues et 3 billes rouges. Lorsque nous tirons des billes sans remplacement, chaque tirage affecte les probabilités des tirages suivants.

Premier tirage - probabilité de bleu : P(blue₁) = 5/8

Deuxième tirage, le premier étant bleu : P(bleu₂ | bleu₁) = 4/7

Cet exemple complète notre précédent exemple de carte en mettant en évidence les dépendances séquentielles.

Exemples concrets

Tests médicaux : Évaluer la précision des tests

Les tests médicaux constituent une application parfaite de la probabilité conditionnelle dans l'évaluation de la précision des tests. Pour tout test de diagnostic, nous devons comprendre quatre probabilités conditionnelles essentielles :

1. P(T+ | D+) : Probabilité d'un test positif si le patient est atteint de la maladie (sensibilité) 
2. P(T- | D-) : Probabilité d'un test négatif si le patient n'est pas atteint de la maladie (spécificité) 
3. P(T+ | D-) : Probabilité d'un test positif alors que le patient n'est pas atteint de la maladie (taux de faux positifs) 
4. P(T- | D+) : Probabilité d'un test négatif si le patient est atteint de la maladie (taux de faux négatifs)

Lors de l'évaluation des performances de ce test, les professionnels de la santé utilisent ces probabilités conditionnelles pour.. :

1. Comparer la précision des tests pour différentes populations de patients
2. Déterminer si plusieurs tests sont nécessaires
3. Fixer des seuils appropriés pour les résultats positifs/négatifs

Par exemple, si nous testons 1000 patients et obtenons 100 résultats positifs, nous pouvons utiliser ces probabilités conditionnelles pour estimer le nombre de vrais positifs par rapport aux faux positifs. Cette analyse aide les professionnels de la santé à mettre en balance les risques de passer à côté d'un diagnostic et les coûts et l'anxiété liés aux fausses alertes.

Évaluation du risque financier

Les entreprises d'investissement utilisent la probabilité conditionnelle pour évaluer les risques du marché. Prenons le cas d'un gestionnaire de portefeuille qui suit la volatilité du marché :

La volatilité quotidienne du marché peut être faible (L), moyenne (M) ou élevée (H).

Les données historiques le montrent : 

• P(H demain | H aujourd'hui) = 0,70 
• P(M demain | H aujourd'hui) = 0,25 
• P(L demain | H aujourd'hui) = 0,05

Ces informations aident les gestionnaires :

• Ajuster l'allocation des portefeuilles en fonction des conditions actuelles du marché
• Fixer des seuils de risque pour les systèmes de négociation automatisés
• Élaborer des plans d'urgence pour les périodes de forte volatilité prolongée

Probabilité conditionnelle et théorème de Bayes

Notre exploration des tests médicaux a mis en évidence une distinction importante : La probabilité d'être atteint d'une maladie en cas de test positif diffère de la probabilité d'être testé positif en cas de maladie. Le théorème de Bayes fournit un cadre formel pour naviguer dans cette relation, ce qui nous permet de mettre à jour nos estimations de probabilité au fur et à mesure que de nouvelles preuves apparaissent.

Comprendre le théorème de Bayes

Le théorème de Bayes exprime la relation entre deux probabilités conditionnelles : P(A|B) = [P(B|A) × P(A)] / P(B). Nous lisons cette équation de la manière suivante : "La probabilité de A étant donné B est égale à la probabilité de B étant donné A multipliée par la probabilité de A, divisée par la probabilité de B."

Chaque composant joue un rôle :

• P(A) : La probabilité préalable - notre croyance initiale au sujet de A avant d'avoir vu la preuve B
• P(B|A) : La probabilité - la probabilité que la preuve B soit vraie si A est vrai
• P(B) : La probabilité totale d'observer la preuve B
• P(A|B) : La probabilité postérieure - notre croyance actualisée sur A après avoir vu la preuve B

Voyons comment cela fonctionne en pratique avec notre scénario de test médical, maintenant élargi pour montrer l'analyse bayésienne complète.

Un exemple de test médical

Prenons l'exemple d'une maladie qui touche 2 % de la population. Un nouveau test de diagnostic a été mis au point :

• Sensibilité de 95 % : P(test positif | a une condition) = 0,95
• 90% de spécificité : P(test négatif | pas de condition) = 0,90

Lorsqu'un patient est testé positif, comment devons-nous actualiser notre opinion sur son état de santé ?

Résolvons ce problème étape par étape :

1. Probabilité antérieure (avant le test) : P(condition) = 0,02 (taux de population de 2%)
2. Probabilité d'un test positif compte tenu de la condition : P(positif|condition) = 0,95 (sensibilité du test)
3. Probabilité totale d'un test positif : P(positif) = P(positif|condition) × P(condition) + P(positif|sans condition) × P(sans condition) = 0,95 × 0,02 + 0,10 × 0,98 = 0,019 + 0,098 = 0,117
4. Probabilité postérieure (en utilisant le théorème de Bayes) : P(condition|positive) = [0,95 × 0,02] / 0,117 ≈ 0,162 ou 16,2 %.

Cette analyse révèle que même avec un test positif, la probabilité d'être atteint de la maladie n'est que d'environ 16,2 % - ce qui est beaucoup plus élevé que les 2 % initiaux, mais peut-être moins que ce que l'intuition pourrait suggérer.

La puissance de la mise à jour bayésienne

Le théorème de Bayes s'impose lorsque nous recevons plusieurs éléments de preuve. La probabilité postérieure de chaque calcul devient la probabilité antérieure pour la prochaine mise à jour. Par exemple, si notre patient obtient un deuxième test positif :

1. Nouvel an : P(condition) = 0,162 (d'après notre premier calcul)
2. Probabilité : P(positif|condition) = 0,95
3. Calculez la nouvelle valeur postérieure...

Cette mise à jour séquentielle fournit un cadre mathématique pour l'intégration de nouvelles données dans nos estimations de probabilité. La beauté de l'inférence bayésienne réside dans sa capacité à quantifier l'évolution de nos croyances au fur et à mesure que nous recueillons de nouvelles informations, en fournissant une méthode formelle de mise à jour des probabilités à la lumière des preuves.

Applications en science des données

Voyons comment la probabilité conditionnelle apparaît dans la science des données. 

Modélisation prédictive

Le classificateur Naive Bayes, l'un des outils les plus simples et les plus puissants de l'apprentissage automatique, applique le théorème de Bayes pour prédire les catégories sur la base des probabilités des caractéristiques. Lors de la classification d'un courrier électronique en tant que spam ou non, par exemple, l'algorithme calcule la probabilité conditionnelle qu'un courrier électronique soit un spam compte tenu des mots qu'il contient. Bien qu'elle repose sur l'hypothèse "naïve" que les caractéristiques sont indépendantes, cette simplification fonctionne souvent étonnamment bien dans la pratique.

Les arbres de décision adoptent une approche différente de la probabilité conditionnelle, en divisant les données sur la base des valeurs des caractéristiques pour créer des sous-ensembles conditionnels. À chaque nœud, l'arbre pose des questions telles que "Quelle est la probabilité de notre variable cible compte tenu de cette valeur de caractéristique spécifique ?" Ces divisions se poursuivent jusqu'à ce que nous atteignions des sous-ensembles purs ou presque purs, créant ainsi une carte de probabilités conditionnelles qui guide nos prédictions.

Gestion des risques

Les systèmes d'évaluation du crédit utilisent des probabilités conditionnelles pour évaluer la probabilité de défaillance d'un prêt en fonction de diverses caractéristiques du client. Par exemple, une banque peut calculer la probabilité d'un défaut de paiement en fonction du niveau de revenu, des antécédents de crédit et de la situation professionnelle. Ces calculs deviennent plus sophistiqués lorsque l'on considère des risques dépendants multiples, comme la manière dont la probabilité de défaut de paiement d'un prêt hypothécaire pourrait changer en cas de récession et de hausse des taux d'intérêt. Les modèles de risque d'investissement utilisent des probabilités conditionnelles pour estimer la valeur à risque (VaR), en calculant la probabilité de niveaux de perte spécifiques compte tenu des conditions actuelles du marché. Les gestionnaires de portefeuille utilisent ces probabilités conditionnelles pour ajuster la répartition des actifs, en comprenant comment le risque d'un investissement peut changer en fonction de la performance des autres investissements du portefeuille.

Apprentissage automatique

Les réseaux bayésiens représentent l'application la plus directe de la probabilité conditionnelle dans l'apprentissage automatique. Ils modélisent les relations entre les variables sous la forme d'un graphe orienté où l'état de chaque nœud dépend de ses parents. Ces réseaux excellent dans des tâches telles que le diagnostic médical, où la probabilité de diverses affections dépend de multiples symptômes et résultats de tests interconnectés.

Les modèles graphiques probabilistes utilisent des dépendances conditionnelles pour représenter des relations complexes dans les données, ce qui les rend précieux pour des tâches telles que la reconnaissance d'images et le traitement du langage naturel. Même les modèles d'apprentissage profond, bien qu'ils ne soient pas explicitement probabilistes, émettent des probabilités conditionnelles dans leurs couches finales lorsqu'ils effectuent des classifications. La fonction softmax, couramment utilisée dans les réseaux neuronaux, transforme les scores bruts en probabilités conditionnelles, nous indiquant la probabilité de chaque classe possible compte tenu des données d'entrée.

Pièges et interprétations erronées

Lorsque l'on travaille sur les probabilités conditionnelles, trois idées fausses principales conduisent souvent à des conclusions erronées.

• L'erreur inverse, également connue sous le nom de confusion de l'inverse, se produit lorsque nous confondons P(A|B) avec P(B|A). Nous l'avons vu dans notre exemple de test médical : la probabilité d'être atteint d'une maladie en cas de test positif diffère de la probabilité d'être testé positif si l'on est atteint de la maladie.
• La négligence du taux de base se produit lorsque nous nous concentrons sur les probabilités conditionnelles en ignorant la probabilité sous-jacente d'un événement. Par exemple, si une maladie rare n'affecte qu'une personne sur 10 000, même un test très précis pourrait donner lieu à une majorité de faux positifs, simplement parce que la maladie est si rare.
• Le troisième écueil concerne l'évaluation incorrecte des preuves lors de la mise à jour des probabilités. Les gens ont tendance à privilégier les preuves récentes ou spectaculaires et à sous-estimer les informations de fond stables. Dans les opérations financières, par exemple, les investisseurs peuvent réagir de manière excessive aux nouvelles récentes du marché tout en ignorant les probabilités de marché à long terme.

Sujets avancés et autres considérations

Enfin, examinons quelques idées plus complexes qui s'appuient sur ce que nous avons pratiqué.

Conditionnement des événements à probabilité nulle

Lorsque nous passons des distributions de probabilités discrètes aux distributions continues, nous rencontrons un défi intéressant : certains points d'une distribution continue ont une probabilité nulle. Prenons l'exemple de la mesure de la taille exacte d'une personne : alors que nous pourrions dire que la probabilité qu'une personne mesure entre 170 et 171 centimètres est significative, la probabilité qu'une personne mesure exactement 170,5432... centimètres est techniquement nulle. Pourtant, nous voulons souvent conditionner des mesures aussi précises. Les probabilités conditionnelles régulières fournissent un cadre mathématique pour traiter ces situations, en étendant nos concepts de base aux cas continus grâce à l'utilisation des fonctions de densité et de la théorie des mesures. Cette extension nous permet de donner un sens à des énoncés tels que "la distribution de probabilité du poids d'une personne, étant donné qu'elle mesure exactement 170,5 centimètres".

Probabilités conditionnelles partielles et extensions

La conditionnalisation de Jeffrey étend la probabilité conditionnelle traditionnelle aux situations dans lesquelles notre nouvelle preuve n'est pas certaine mais s'accompagne de sa propre probabilité. Contrairement au conditionnement standard, qui suppose une certitude absolue quant aux nouvelles informations, la règle de Jeffrey nous permet d'actualiser nos croyances sur la base de preuves incertaines. Cela correspond mieux aux scénarios du monde réel où les nouvelles informations sont souvent accompagnées d'un certain degré d'incertitude. Par exemple, plutôt que de savoir avec certitude qu'un test médical est positif, nous pourrions apprendre qu'il a 80 % de chances d'être positif. La règle de Jeffrey fournit une méthode formelle pour mettre à jour les probabilités dans ces situations plus nuancées.

Conclusion

La probabilité conditionnelle fournit un cadre mathématique pour la mise à jour de nos croyances au fur et à mesure de l'apparition de nouvelles informations. Tout au long de cet article, nous avons vu comment ce concept s'applique à différents domaines, du diagnostic médical à l'évaluation des risques financiers. Les principes que nous avons explorés nous aident à comprendre comment les probabilités changent avec de nouvelles preuves, ce qui permet de prendre des décisions plus éclairées dans les applications de la science des données. Cette compréhension devient particulièrement précieuse lorsque vous travaillez avec des algorithmes de classification, des modèles de risque et des systèmes d'apprentissage automatique où les mises à jour des probabilités se font en continu.

Alors que vous continuez à développer votre expertise en matière de probabilités et d'inférence statistique, plusieurs cours peuvent améliorer votre compréhension de ces concepts dans une optique bayésienne. Notre cours Fundamentals of Bayesian Data Analysis in R présente les principes clés et leurs applications pratiques, tandis que notre cours Bayesian Modeling with RJAGS montre comment mettre en œuvre ces concepts à l'aide d'outils statistiques puissants. Pour les utilisateurs de Python, notre cours Analyse de données bayésiennes en Python offre une expérience pratique de l'application de ces méthodes à des problèmes réels. Chaque cours vous permet d'approfondir votre connaissance des probabilités et de leurs applications dans la science des données moderne.