Probabilidad compuesta: Definición, reglas y ejemplos

Estás tirando dos dados en un juego de mesa. ¿Qué probabilidades hay de que saques un seis en ambos? O tal vez estés analizando datos de clientes y necesites saber la probabilidad de que un usuario haga clic en un anuncio o realice una compra.

Estos escenarios implican una probabilidad compuesta, que calcula la probabilidad de que se produzcan múltiples eventos, ya sea de forma conjunta o por separado. Si te parece confuso, no te preocupes: Haré que las ideas sean fáciles de seguir con ejemplos claros.

¿Qué es la probabilidad compuesta?

La probabilidad compuesta calcula la probabilidad cuando hay dos o más eventos involucrados. La probabilidad simple se centra en un único evento (como lanzar una moneda), pero la probabilidad compuesta aborda situaciones en las que pueden ocurrir varias cosas.

En estadística formal, estos escenarios tienen nombres específicos: el escenario AND es la probabilidad conjunta (la probabilidad de que ambos eventos ocurran juntos), y el escenario OR es la unión (la probabilidad de que ocurra al menos uno de los eventos).

Piensa en la probabilidad compuesta como un término genérico fácil de entender para principiantes que te ayuda a aprender ambos tipos de cálculos antes de adentrarte en términos más técnicos.

Tipos de eventos de probabilidad compuesta

La distinción AND/OR te indica qué fórmula debes utilizar, pero existe otra relación entre los eventos que modifica el funcionamiento de esas fórmulas. Antes de poder calcular con precisión las probabilidades compuestas, es necesario comprender cómo se relacionan los eventos entre sí. En concreto, si un evento influye en el otro.

Eventos independientes

Dos eventos son independientes cuando uno no afecta al otro. Lanza una moneda al aire y luego tira un dado. Sacar caras no cambia tus posibilidades de sacar un cuatro. Cada evento tiene su propia probabilidad, que se mantiene constante.

Algunos ejemplos clásicos son tirar varios dados, lanzar varias monedas o robar cartas con reemplazo (volver a colocar cada carta antes de la siguiente tirada). En la ciencia de datos, verás independencia al analizar sesiones de usuario separadas o grupos de pruebas A/B no relacionados.

Eventos dependientes

Los eventos son dependientes cuando el primer evento cambia la probabilidad del segundo. Robar una carta de un mazo y luego robar otra sin devolver la primera. La segunda tirada tiene probabilidades diferentes porque la composición del mazo ha cambiado.

Verás eventos dependientes cuando realices muestreos sin reemplazo, en procesos de decisión secuenciales o cuando los eventos estén causalmente vinculados. La probabilidad de una segunda compra depende de si el cliente realizó una primera compra. Esta dependencia afecta directamente a tus cálculos.

Reglas para calcular la probabilidad compuesta

Ahora que ya entiendes las relaciones entre eventos, podemos abordar los cálculos propiamente dichos.

La independencia o dependencia que acabas de aprender determina directamente qué versión de la fórmula utilizarás. El método de cálculo depende de si se trata de escenarios AND u OR y, dentro de esos escenarios, de si los eventos son independientes o dependientes.

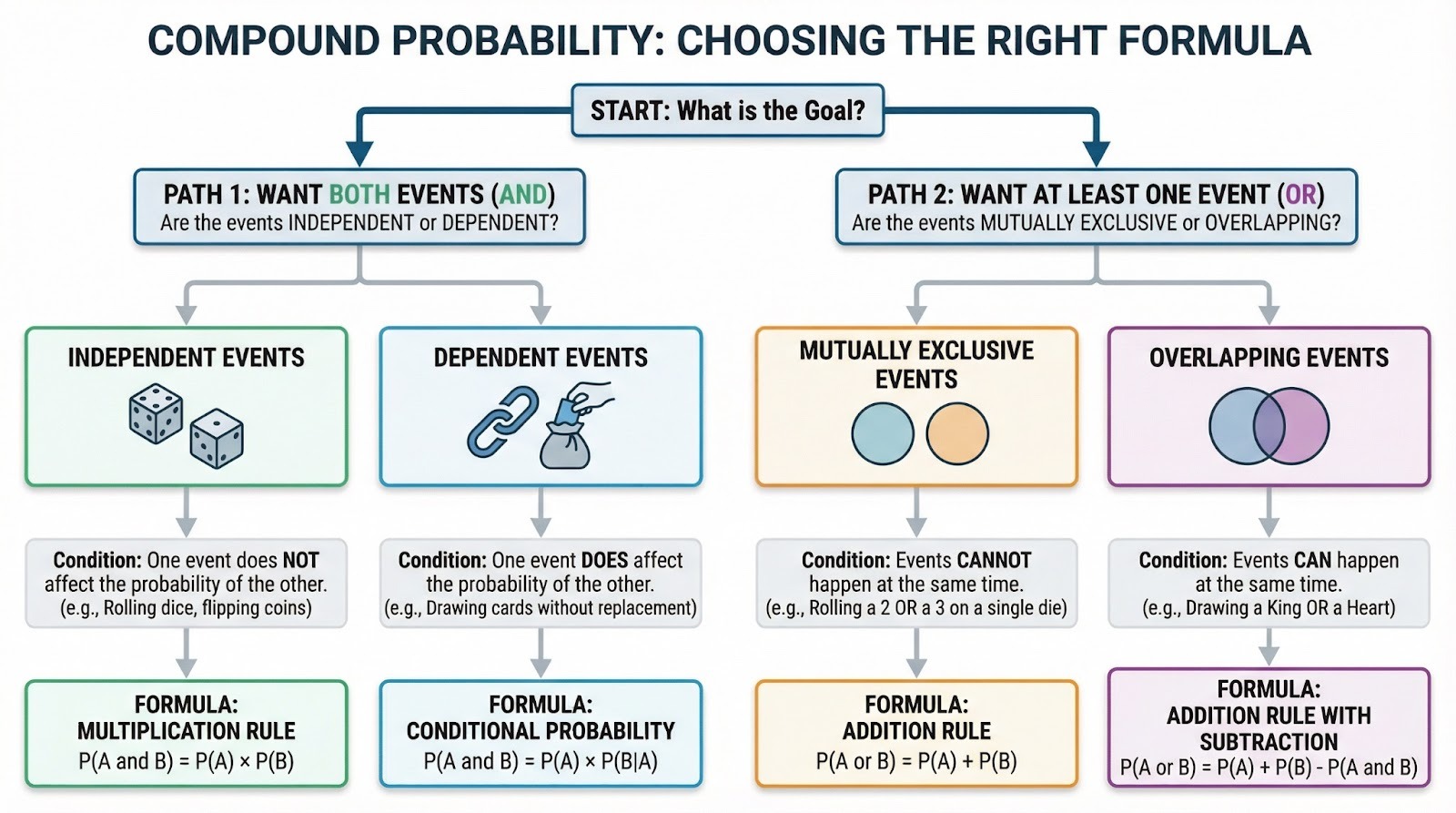
Diagrama de flujo de decisiones para elegir la fórmula de probabilidad compuesta correcta. Imagen del autor.

La regla de la multiplicación

La regla de multiplicación maneja escenarios AND (cuando deseas que ocurran ambos eventos). Para eventos independientes, multiplicad sus probabilidades individuales: P(A ∩ B) = P(A) × P(B). ¿Sacar un cuatro Y que salga cara? Eso es (1/6) × (1/2) = 1/12.

Para eventos dependientes, necesitarás la probabilidad condicional: P(A ∩ B) = P(A) × P(B|A). Esto significa «la probabilidad de A multiplicada por la probabilidad de B, dado que A ha ocurrido». ¿Sacar dos ases sin reemplazo? El primer as es 4/52, pero el segundo as ahora es 3/51 porque estás robando de un mazo más pequeño. Multiplícalos: (4/52) × (3/51) = 1/221.

La regla de suma (cuando los eventos se superponen)

La regla de suma maneja escenarios OR (cuando deseas que ocurra al menos un evento). Si los eventos no pueden ocurrir simultáneamente (son mutuamente excluyentes), simplemente añade: P(A or B) = P(A) + P(B). Sacar un dos O un tres en un dado significa 1/6 + 1/6 = 1/3.

Cuando los eventos pueden solaparse, es necesario restar la intersección para evitar el doble recuento: P(A o B) = P(A) + P(B) - P(A ∩ B). ¿Sacar un rey O un corazón de una baraja? Hay 4 reyes y 13 corazones, pero el rey de corazones se cuenta dos veces, por lo que: 4/52 + 13/52 - 1/52 = 16/52.

Ejemplos paso a paso de probabilidad compuesta

Veamos cómo se aplican estas reglas con ejemplos concretos. La probabilidad compuesta es un término genérico que abarca tanto los escenarios de eventos independientes como los de eventos dependientes.

Ejemplo con eventos independientes

Lanzas una moneda imparcial dos veces. ¿Cuál es la probabilidad de que salga cara las dos veces? Dado que los lanzamientos de la moneda son independientes, cada lanzamiento tiene una probabilidad de 1/2. Usando la regla de multiplicación: P(cara en el lanzamiento 1 Y cara en el lanzamiento 2) = 1/2 × 1/2 = 1/4. Hay un 25 % de probabilidades de que salgan dos caras seguidas.

Ejemplo con eventos dependientes

Una bolsa contiene 5 canicas azules y 3 canicas rojas. Tú sacas dos canicas sin reemplazo. ¿Cuál es la probabilidad de que ambos sean azules? El primer sorteo tiene una probabilidad de 5/8. Después de sacar una canica azul, solo quedan 4 canicas azules en una bolsa de 7, por lo que P(Azul en la segunda extracción | Azul en la primera) = 4/7. Por lo tanto: P(Ambos azules) = 5/8 × 4/7 = 20/56 = 5/14, aproximadamente el 35,7 %.

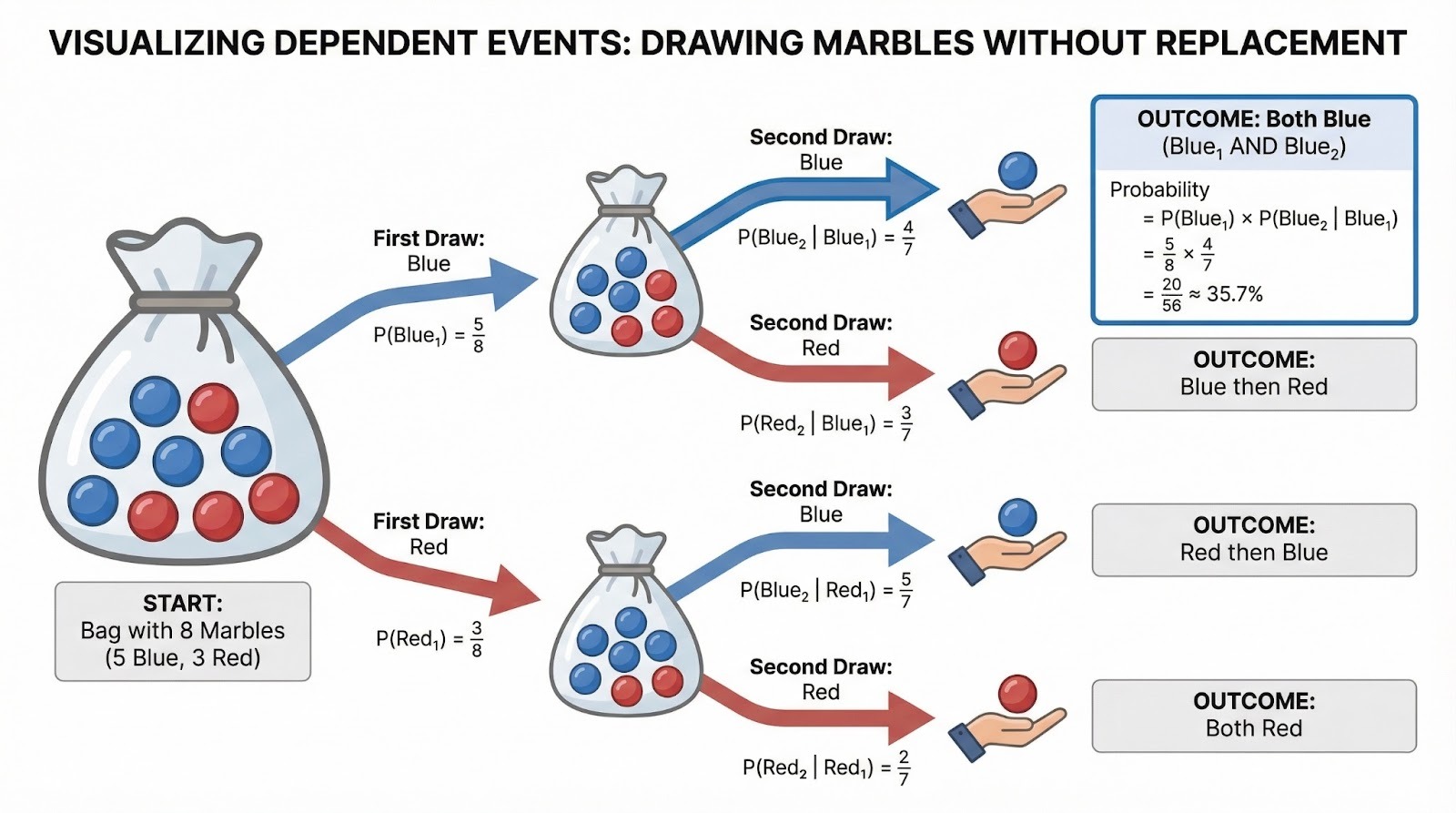
Diagrama de árbol que visualiza eventos dependientes al sacar canicas sin reemplazo. Imagen del autor.

Ejemplo con «AND» frente a «OR»

Aquí es importante leer con atención. Se lanza un dado estándar. ¿Cuál es la probabilidad de sacar un número menor que 3 O un número par? Números menores que 3: {1, 2}. Números pares: {2, 4, 6}. Estos se superponen en 2, por lo que no podemos simplemente sumarlos. Usando la regla de la suma: P(Menos de 3) = 2/6, P(Par) = 3/6, P(Ambos) = 1/6. Por lo tanto: 2/6 + 3/6 - 1/6 = 4/6 = 2/3.

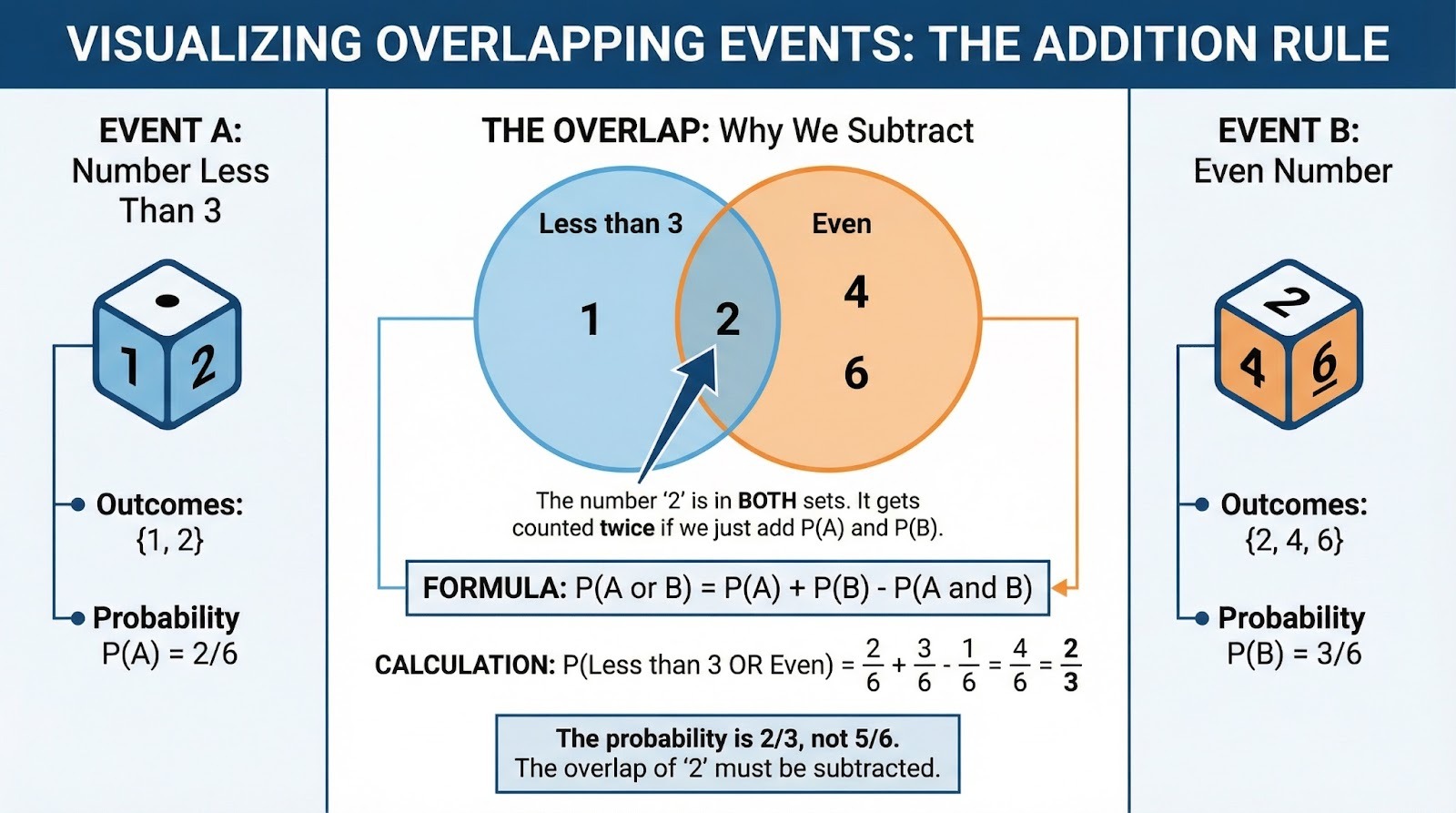
Diagrama de Venn que muestra eventos superpuestos. Imagen del autor.

Observa cómo la palabra «o» indica que necesitamos una suma, mientras que «y» indicaría una multiplicación. El lenguaje utilizado en las preguntas de probabilidad te indica qué regla debes aplicar.

Errores de probabilidad compuesta

Tratar eventos dependientes como independientes es el error más frecuente. Si sacas cartas sin reemplazo, pero multiplicas las probabilidades como si el mazo no cambiara, tu respuesta será incorrecta. Pregunta siempre: ¿el primer evento cambia las condiciones para el segundo?

La suma de probabilidades cuando se requiere una multiplicación ocurre cuando las personas malinterpretan «y» como «o». Si una pregunta solicita la probabilidad del evento A Y el evento B, se multiplica (suponiendo independencia o utilizando probabilidad condicional). Al añadirlo, se obtiene un escenario completamente diferente.

Malinterpretar «y» frente a «o» causa confusión porque el lenguaje cotidiano es menos preciso que el lenguaje matemático. «¿Qué probabilidades hay de que llueva o nieve mañana?» significa al menos una de las dos cosas, no ambas (eso sería una suma). «¿Qué probabilidades hay de que llueva y nieve mañana?» significa que ocurran ambas cosas (es decir, una multiplicación).

Olvidarse de ajustar las probabilidades después de que se produce un resultado aparece en escenarios secuenciales. Después de robar una carta, el mazo tiene 51 cartas, no 52. Cuando un cliente se va, tienes uno menos en tu muestra. Actualiza tus probabilidades en cada paso.

Cómo se manifiesta la probabilidad compuesta

En los juegos de azar, los casinos utilizan la probabilidad compuesta para calcular la ventaja de la casa. Comprender la probabilidad de múltiples resultados favorables ayuda a los jugadores a tomar decisiones de apuestas informadas (aunque la casa siempre tiene su ventaja matemática incorporada). El análisis de riesgos en los negocios y las finanzas se basa en gran medida en la probabilidad compuesta. ¿Cuál es la probabilidad de que se produzca una caída del mercado Y un aumento de los tipos de interés? Estos escenarios compuestos ayudan a las empresas a protegerse contra múltiples factores de riesgo que se producen simultáneamente.

Los procesos de control de calidad utilizan la probabilidad compuesta para evaluar la probabilidad de que se produzcan defectos. Si dos etapas de fabricación tienen cada una una tasa de defectos del 2 %, la probabilidad compuesta te indica la tasa de defectos global de los productos que pasan por ambas etapas. Las pruebas médicas combinan múltiples resultados de pruebas utilizando la probabilidad compuesta. Un paciente puede someterse a varias pruebas diagnósticas, y los médicos necesitan conocer la probabilidad de enfermedad teniendo en cuenta todos los resultados de las pruebas en conjunto, no solo una prueba aislada.

Nuestro curso Fundamentos de probabilidad en Python cubreen profundidad aplicaciones prácticas comoestas.

Probabilidad compuesta frente a Probabilidad condicional

La probabilidad condicional pregunta: Dado que ocurrió B, ¿cuál es la probabilidad de que ocurra A? Estás encalculando tu probabilidad estimada basándote en nueva información. La probabilidad compuesta pregunta: ¿Cuál es la probabilidad de que se produzcan varios eventos en alguna combinación?

Se conectan al calcular la probabilidad compuesta para eventos dependientes. Utilizas la probabilidad condicional en tu regla de multiplicación. P(A ∩ B) = P(A) × P(B|A) muestra esta relación de forma explícita. La probabilidad condicional P(B|A) te ayuda a calcular la probabilidad compuesta de A y B.

Piénsalo de esta manera. La probabilidad condicional es una herramienta que se utiliza en los cálculos de probabilidad compuesta. Cuando los eventos son dependientes, no puedes calcular probabilidades compuestas sin tener en cuenta cómo un evento afecta a otro, y eso es exactamente lo que mide la probabilidad condicional.

Consejos prácticos para resolver problemas de probabilidad compuesta

Comienza por identificar cuántos eventos hay y si son independientes o dependientes. Busca pistas: ¿el problema menciona la sustitución? ¿Un evento cambia las condiciones para el siguiente? Los eventos independientes mantienen sus probabilidades constantes, mientras que los eventos dependientes requieren que actualices las probabilidades después de cada evento.

Traduce «y» o «o» con cuidado, ya que estas palabras determinan todo tu enfoque. Escribe lo que sabes antes de calcular. Enumera las probabilidades individuales, identifica las probabilidades condicionales y dibuja un diagrama rápido si estás trabajando con eventos secuenciales. Este trabajo previo evita errores cuando empiezas a calcular.

Comprueba que tus resultados sean razonables. Las probabilidades deben estar entre 0 y 1. Si multiplicas probabilidades, tu respuesta debería ser menor que la probabilidad individual más pequeña. Si algo parece estar mal, revisa tu trabajo antes de pasar a una sala e. Nuestro curso Probabilidad Puzzles en R ofrece práctica con estas estrategias de resolución de problemas.

Conclusión

La probabilidad compuesta te proporciona el marco matemático necesario para manejar múltiples eventos en combinación. La clave está en reconocer si se trata de situaciones AND (regla de multiplicación) o OR (regla de suma), y si los eventos son independientes o dependientes. Estas distinciones determinan qué fórmula utilizarás.

Con la práctica, desarrollarás intuición para resolver estos problemas. Las aplicaciones del mundo real en la ciencia de datos (desde las pruebas A/B hasta la modelización de riesgos) utilizan estos mismos principios. Comienza con ejemplos sencillos, sigue la lógica paso a paso y gana confianza con situaciones cada vez más complejas.