Zusammengesetzte Wahrscheinlichkeit: Definition, Regeln und Beispiele

Du würfelst mit zwei Würfeln in einem Brettspiel. Wie hoch ist die Chance, dass du bei beiden eine Sechs würfelst? Oder vielleicht analysierst du Kundendaten und musst wissen, wie hoch die Wahrscheinlichkeit ist, dass ein Nutzer entweder auf eine Anzeige klickt oder einen Kauf tätigt.

Bei diesen Szenarien geht's um die zusammengesetzte Wahrscheinlichkeit, die die Wahrscheinlichkeit mehrerer Ereignisse berechnet, egal ob sie zusammen oder getrennt auftreten. Wenn das verwirrend klingt, mach dir keine Sorgen: Ich werde die Ideen mit klaren Beispielen leicht verständlich machen.

Was ist eine zusammengesetzte Wahrscheinlichkeit?

Die zusammengesetzte Wahrscheinlichkeit berechnet, wie wahrscheinlich es ist, dass zwei oder mehr Ereignisse zusammen auftreten. Einfache Wahrscheinlichkeit dreht sich um ein einzelnes Ereignis (wie das Werfen einer Münze), aber zusammengesetzte Wahrscheinlichkeit geht um Situationen, in denen mehrere Sachen passieren können.

In der formalen Statistik haben diese Szenarien bestimmte Namen: Das UND-Szenario ist die gemeinsame Wahrscheinlichkeit (die Wahrscheinlichkeit, dass beide Ereignisse zusammen auftreten), und das ODER-Szenario ist die Vereinigung (die Wahrscheinlichkeit, dass mindestens ein Ereignis auftritt).

Stell dir die zusammengesetzte Wahrscheinlichkeit als einen anfängerfreundlichen Oberbegriff vor, der dir hilft, beide Arten von Berechnungen zu lernen, bevor du dich mit diesen eher technischen Begriffen beschäftigst.

Arten von zusammengesetzten Wahrscheinlichkeitsereignissen

Die Unterscheidung zwischen UND/ODER sagt dir, welche Formel du nehmen musst, aber es gibt noch eine andere Beziehung zwischen Ereignissen, die die Funktionsweise dieser Formeln verändert. Bevor du zusammengesetzte Wahrscheinlichkeiten genau berechnen kannst, musst du verstehen, wie Ereignisse miteinander zusammenhängen. Genauer gesagt, ob das eine Ereignis das andere beeinflusst.

Unabhängige Ereignisse

Zwei Ereignisse sind unabhängig voneinander, wenn das eine das andere nicht beeinflusst. Wirf eine Münze und würfel dann. Köpfe zu bekommen ändert nichts an deinen Chancen, eine Vier zu würfeln. Jedes Ereignis hat seine eigene Wahrscheinlichkeit, die immer gleich bleibt.

Typische Beispiele sind das Werfen mehrerer Würfel, das Werfen mehrerer Münzen oder das Ziehen von Karten mit Zurücklegen (jede Karte wird vor dem nächsten Zug zurückgelegt). In der Datenwissenschaft siehst du Unabhängigkeit, wenn du einzelne Benutzersitzungen oder nicht miteinander verbundene A/B-Testgruppen analysierst.

Abhängige Ereignisse

Ereignisse hängen voneinander ab, wenn das erste Ereignis die Wahrscheinlichkeit des zweiten Ereignisses verändert. Zieh eine Karte vom Stapel und dann noch eine, ohne die erste zurückzulegen. Die zweite Ziehung hat andere Chancen, weil sich die Zusammensetzung des Kartenspiels geändert hat.

Du siehst abhängige Ereignisse, wenn du ohne Ersatz stichprobenartig vorgehst, in sequenziellen Entscheidungsprozessen oder wenn Ereignisse kausal miteinander verbunden sind. Die Wahrscheinlichkeit, dass jemand was nochmal kauft, hängt davon ab, ob er schon mal was gekauft hat. Diese Abhängigkeit wirkt sich direkt auf deine Berechnungen aus.

Regeln zur Berechnung der zusammengesetzten Wahrscheinlichkeit

Jetzt, wo du die Beziehungen zwischen den Ereignissen verstehst, können wir uns den eigentlichen Berechnungen widmen.

Die Unabhängigkeit oder Abhängigkeit, die du gerade kennengelernt hast, entscheidet direkt, welche Version der Formel du verwenden wirst. Die Berechnungsmethode hängt davon ab, ob du es mit UND- oder ODER-Szenarien zu tun hast und ob deine Ereignisse innerhalb dieser Szenarien unabhängig oder abhängig voneinander sind.

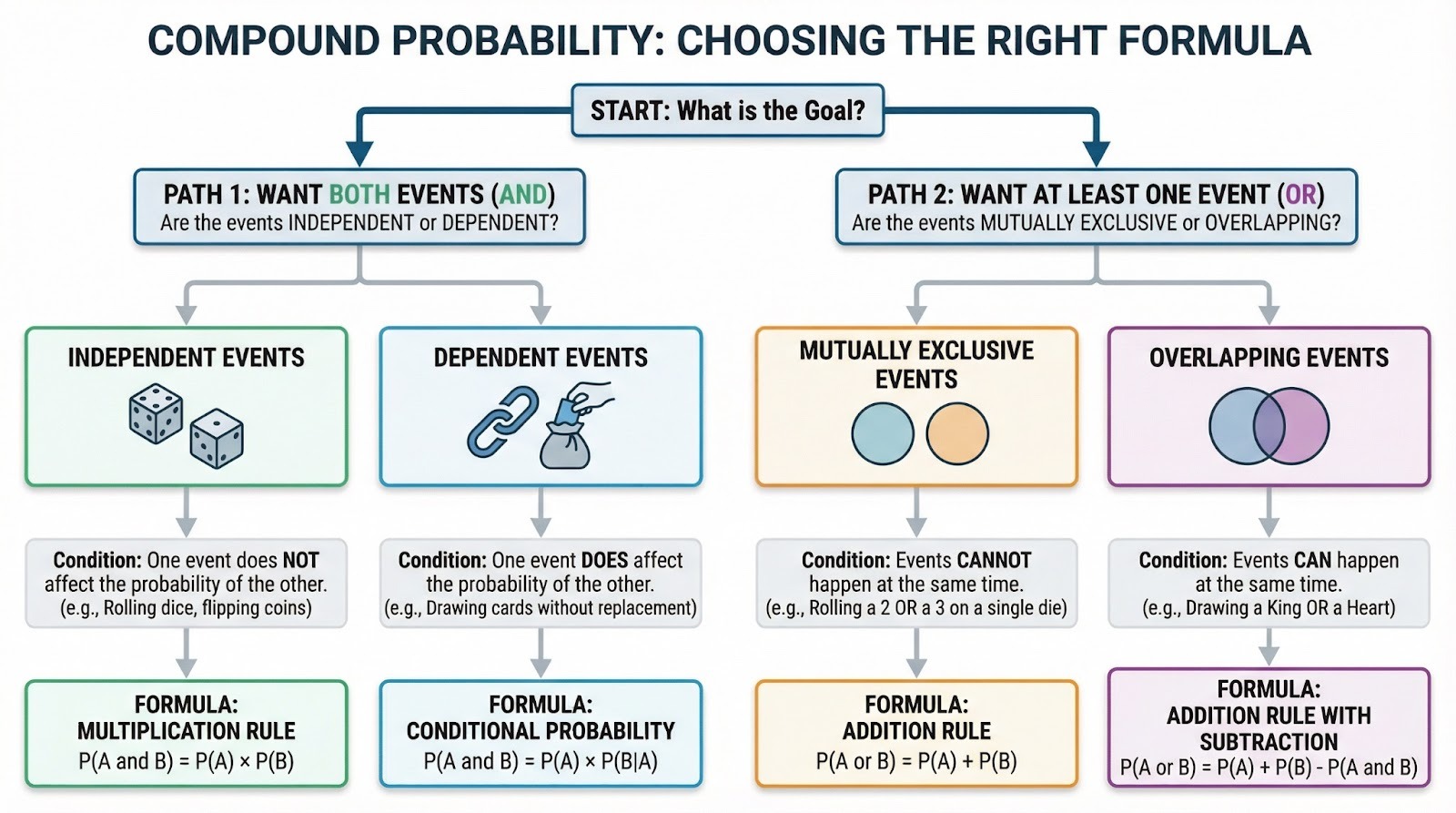
Entscheidungsdiagramm zur Auswahl der richtigen Formel für die zusammengesetzte Wahrscheinlichkeit. Bild vom Autor.

Die Multiplikationsregel

Die Multiplikationsregel gilt für UND-Szenarien (wenn du willst, dass beide Ereignisse eintreten). Für unabhängige Ereignisse multipliziert man ihre einzelnen Wahrscheinlichkeiten: P(A ∩ B) = P(A) × P(B). Eine Vier würfeln UND Kopf werfen? Das ist (1/6) × (1/2) = 1/12.

Für abhängige Ereignisse brauchst du die bedingte Wahrscheinlichkeit: P(A ∩ B) = P(A) × P(B|A). Das heißt: „Die Wahrscheinlichkeit von A mal die Wahrscheinlichkeit von B, wenn A passiert ist.“ Zwei Asse ziehen, ohne zu tauschen? Das erste Ass ist 4/52, aber das zweite Ass ist jetzt 3/51, weil du aus einem kleineren Kartenspiel ziehst. Multipliziere sie: (4/52) × (3/51) = 1/221.

Die Additionsregel (wenn sich Ereignisse überschneiden)

Die Additionsregel regelt ODER-Szenarien (wenn mindestens ein Ereignis eintreten soll). Wenn Ereignisse nicht gleichzeitig passieren können (sich gegenseitig ausschließen), füge einfach Folgendes hinzu: P(A oder B) = P(A) + P(B). Wenn du mit einem Würfel eine Zwei ODER eine Drei würfelst, bedeutet das 1/6 + 1/6 = 1/3.

Wenn sich Ereignisse überschneiden können, musst du die Überschneidung abziehen, um Doppelzählungen zu vermeiden: P(A oder B) = P(A) + P(B) - P(A ∩ B). Ziehst du einen König ODER eine Herzkarte aus dem Kartenspiel? Es gibt 4 Könige und 13 Herzen, aber der Herzkönig zählt doppelt, also: 4/52 + 13/52 - 1/52 = 16/52.

Schritt-für-Schritt-Beispiele für zusammengesetzte Wahrscheinlichkeiten

Schauen wir uns anhand von konkreten Beispielen an, wie diese Regeln funktionieren. Die zusammengesetzte Wahrscheinlichkeit ist ein Sammelbegriff, der sowohl unabhängige als auch abhängige Ereignisszenarien abdeckt.

Beispiel mit unabhängigen Ereignissen

Du wirfst eine faire Münze zweimal. Wie hoch ist die Wahrscheinlichkeit, dass du zweimal Kopf würfelst? Weil Münzwürfe unabhängig voneinander sind, hat jeder Wurf eine Wahrscheinlichkeit von 1/2. Mit der Multiplikationsregel: P(Kopf beim ersten Wurf UND Kopf beim zweiten Wurf) = 1/2 × 1/2 = 1/4. Die Wahrscheinlichkeit, zweimal hintereinander Kopf zu werfen, liegt bei 25 %.

Beispiel mit abhängigen Ereignissen

In einem Beutel sind 5 blaue Murmeln und 3 rote Murmeln. Du ziehst zwei Murmeln, ohne sie zurückzulegen. Wie hoch ist die Wahrscheinlichkeit, dass beide blau sind? Die erste Ziehung hat eine Wahrscheinlichkeit von 5/8. Nachdem eine blaue Murmel rausgenommen wurde, sind nur noch 4 blaue Murmeln in einem Beutel mit 7 Murmeln übrig, also ist P(Blau beim zweiten Ziehen | Blau beim ersten Ziehen) = 4/7. Also: P(Beide blau) = 5/8 × 4/7 = 20/56 = 5/14, ungefähr 35,7 %.

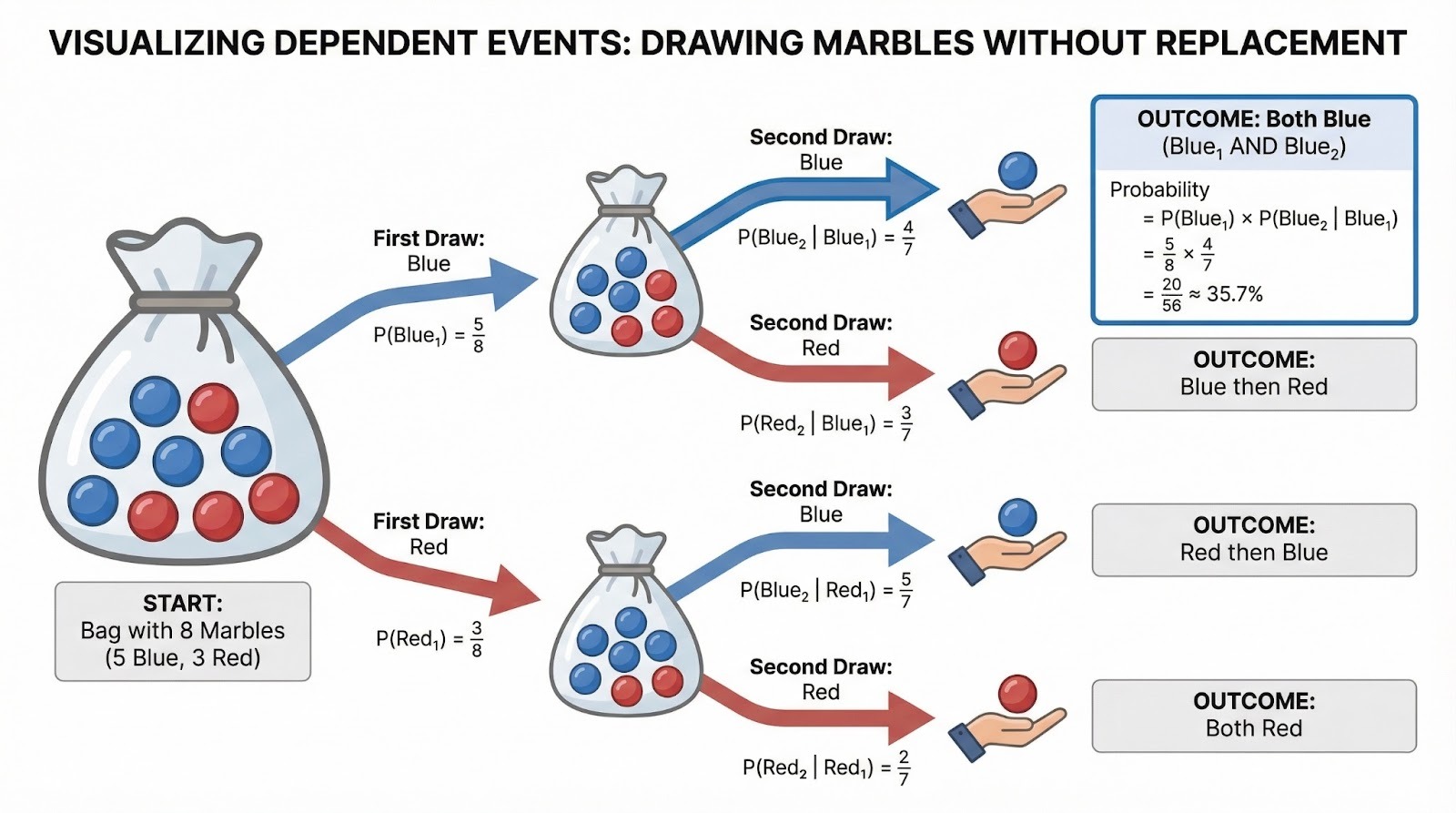
Baumdiagramm, das abhängige Ereignisse beim Ziehen von Murmeln ohne Zurücklegen zeigt. Bild vom Autor.

Beispiel mit „UND“ vs. „ODER“

Hier ist es wichtig, genau zu lesen. Ein Standardwürfel wird geworfen. Wie hoch ist die Chance, eine Zahl unter 3 ODER eine gerade Zahl zu würfeln? Zahlen kleiner als 3: {1, 2}. Gerade Zahlen: {2, 4, 6}. Die überschneiden sich bei 2, also können wir nicht einfach addieren. Mit der Additionsregel: P(weniger als 3) = 2/6, P(gerade) = 3/6, P(beides) = 1/6. Also: 2/6 + 3/6 - 1/6 = 4/6 = 2/3.

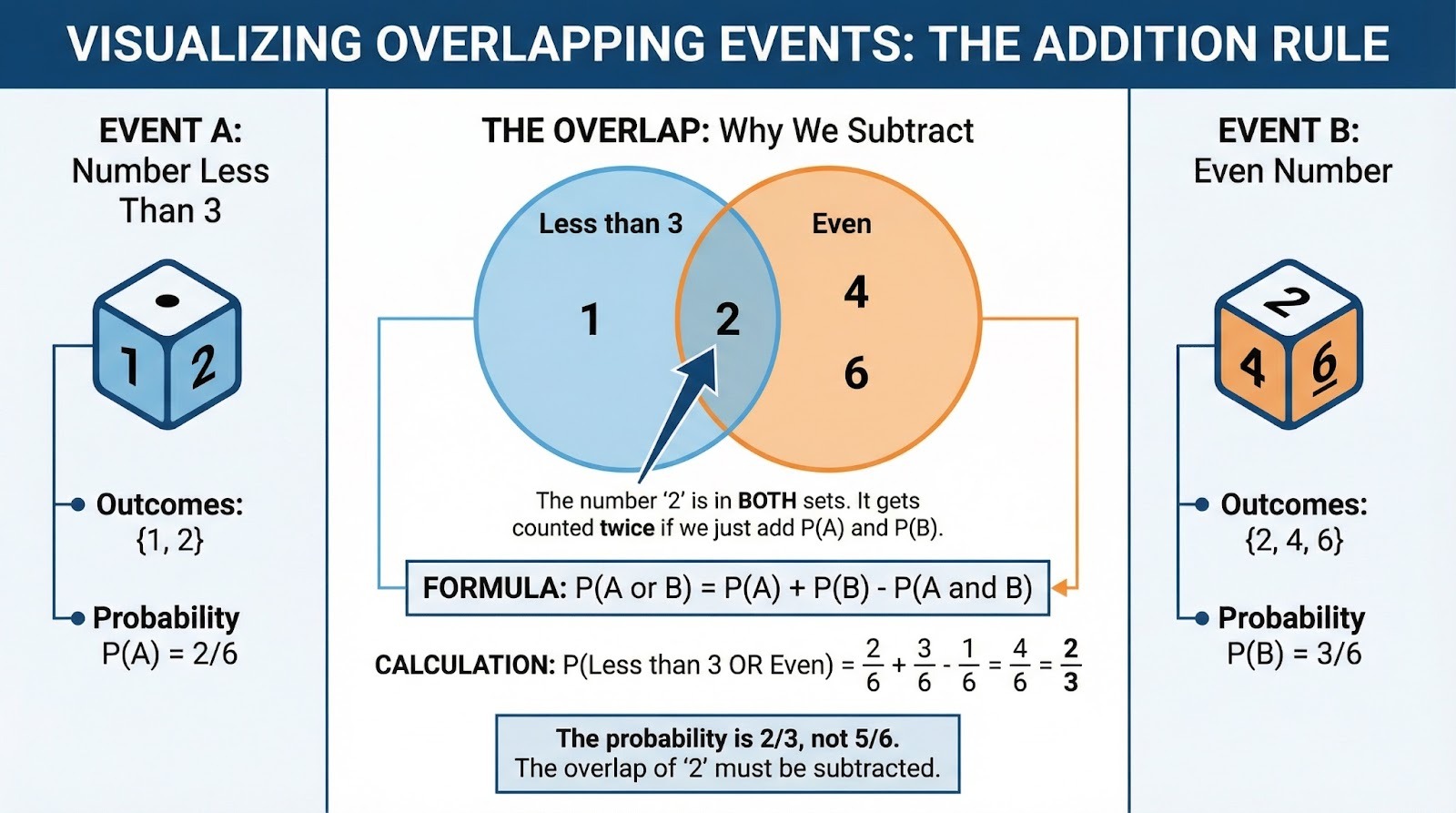
Venn-Diagramm, das sich überschneidende Ereignisse zeigt. Bild vom Autor.

Schau mal, wie das Wort „oder“ zeigt, dass wir addieren müssen, während „und“ eine Multiplikation bedeuten würde. Die Formulierung in Wahrscheinlichkeitsfragen sagt dir, welche Regel du anwenden musst.

Fehler bei der Berechnung von zusammengesetzten Wahrscheinlichkeiten

Abhängige Ereignisse als unabhängig zu behandeln, ist der häufigste Fehler. Wenn du Karten ziehst, ohne sie zu ersetzen, aber die Wahrscheinlichkeiten so multiplizierst, als würde sich das Kartenspiel nicht verändern, ist deine Antwort falsch. Frag dich immer: Ändert das erste Ereignis die Bedingungen für das zweite?

Das Addieren von Wahrscheinlichkeiten, wenn eigentlich multipliziert werden müsste, passiert, wenn Leute „und“ fälschlicherweise als „oder“ verstehen. Wenn in einer Frage nach der Wahrscheinlichkeit von Ereignis A UND Ereignis B gefragt wird, multiplizierst du (unter der Annahme der Unabhängigkeit oder unter Verwendung der bedingten Wahrscheinlichkeit). Wenn du was hinzufügst, bekommst du ein ganz anderes Szenario.

Die falsche Interpretation von „und“ gegenüber „oder“ sorgt für Verwirrung, weil die Alltagssprache nicht so präzise ist wie die mathematische Sprache. „Wie hoch ist die Wahrscheinlichkeit, dass es morgen regnet oder schneit?“ bedeutet mindestens eines davon, nicht beides (das wäre eine Addition). Wie hoch ist die Wahrscheinlichkeit, dass es morgen regnet und schneit? Das heißt, dass beides passiert (das ist eine Multiplikation).

Das Vergessen, die Wahrscheinlichkeiten nach einem Ergebnis anzupassen, zeigt sich in aufeinanderfolgenden Szenarien. Nachdem du eine Karte gezogen hast, hat das Kartenspiel nur noch 51 Karten, nicht mehr 52. Wenn ein Kunde weggeht, hast du einen weniger in deiner Stichprobe. Aktualisier deine Wahrscheinlichkeiten bei jedem Schritt.

Wie sich die zusammengesetzte Wahrscheinlichkeit zeigt

Bei Glücksspielen nutzen Casinos die zusammengesetzte Wahrscheinlichkeit, um den Hausvorteil zu berechnen. Wenn man die Wahrscheinlichkeit mehrerer guter Ergebnisse versteht, kann man bessere Entscheidungen beim Wetten treffen (auch wenn das Haus immer einen mathematischen Vorteil hat). Risikoanalyse in Wirtschaft und Finanzen hängt stark von der zusammengesetzten Wahrscheinlichkeit ab. Wie hoch ist die Wahrscheinlichkeit, dass es sowohl zu einem Marktabschwung als auch zu steigenden Zinsen kommt? Diese kombinierten Szenarien helfen Unternehmen, sich gegen mehrere gleichzeitig auftretende Risikofaktoren abzusichern.

Bei Qualitätskontrollen wird die Wahrscheinlichkeit von Fehlern mit Hilfe der zusammengesetzten Wahrscheinlichkeit eingeschätzt. Wenn zwei Produktionsstufen jeweils eine Fehlerquote von 2 % haben, gibt dir die zusammengesetzte Wahrscheinlichkeit die Gesamtfehlerquote für Produkte an, die beide Stufen durchlaufen. Bei medizinischen Tests werden mehrere Testergebnisse mit Hilfe der zusammengesetzten Wahrscheinlichkeit kombiniert. Ein Patient kann mehrere diagnostische Tests machen, und die Ärzte müssen wissen, wie hoch die Wahrscheinlichkeit einer Krankheit ist, wenn man alle Testergebnisse zusammen betrachtet, nicht nur einen einzelnen Test.

Unser Kurs „Grundlagen der Wahrscheinlichkeit in Python ” gehtausführlich auf solche praktischen Anwendungen ein.

Verbundwahrscheinlichkeit vs. Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit fragt: Wenn B passiert ist, wie hoch ist dann die Chance, dass A passiert ist? Du bist dran,, deine Wahrscheinlichkeitsschätzung auf der Grundlage neuer Informationen anzupassen. Die zusammengesetzte Wahrscheinlichkeit fragt: Wie hoch ist die Wahrscheinlichkeit, dass mehrere Ereignisse in irgendeiner Kombination auftreten?

Sie hängen zusammen, wenn man die kombinierte Wahrscheinlichkeit für abhängige Ereignisse berechnet. Du benutzt die bedingte Wahrscheinlichkeit in deiner Multiplikationsregel. P(A ∩ B) = P(A) × P(B|A) zeigt diese Beziehung ganz klar. Die bedingte Wahrscheinlichkeit P(B|A) hilft dir dabei, die zusammengesetzte Wahrscheinlichkeit von A und B zu berechnen.

Sieh es mal so. Die bedingte Wahrscheinlichkeit ist ein Werkzeug, das du bei der Berechnung von zusammengesetzten Wahrscheinlichkeiten benutzt. Wenn Ereignisse voneinander abhängen, kann man keine zusammengesetzten Wahrscheinlichkeiten berechnen, ohne zu berücksichtigen, wie sich ein Ereignis auf ein anderes auswirkt, und genau das misst die bedingte Wahrscheinlichkeit.

Tipps zum Üben, um Probleme mit zusammengesetzten Wahrscheinlichkeiten zu lösen

Fang damit an, festzustellen, wie viele Ereignisse es gibt und ob sie unabhängig oder abhängig voneinander sind. Such nach Hinweisen: Wird in der Aufgabe ein Austausch erwähnt? Verändert ein Ereignis die Bedingungen für das nächste? Unabhängige Ereignisse behalten ihre Wahrscheinlichkeiten bei, während du bei abhängigen Ereignissen die Wahrscheinlichkeiten nach jedem Ereignis anpassen musst.

Übersetz „und“ oder „oder“ sorgfältig, weil diese Wörter deine ganze Herangehensweise bestimmen. Schreib auf, was du weißt, bevor du rechnest. Schreib die einzelnen Wahrscheinlichkeiten auf, finde alle bedingten Wahrscheinlichkeiten heraus und mach dir ein kurzes Diagramm, wenn du mit aufeinanderfolgenden Ereignissen arbeitest. Diese Vorbereitungsarbeit hilft dir, Fehler beim Rechnen zu vermeiden.

Schau mal, ob deine Ergebnisse im Großen und Ganzen vernünftig sind. Die Wahrscheinlichkeiten müssen zwischen 0 und 1 liegen. Wenn du Wahrscheinlichkeiten multiplizierst, sollte dein Ergebnis kleiner sein als die kleinste einzelne Wahrscheinlichkeit. Wenn dir irgendwas komisch vorkommt, check deine Arbeit nochmal, bevor du weitermachst.ward. Unser Kurs „Probability Puzzles in R ” bietet Übungen zu diesen Problemlösungsstrategien.

Fazit

Die zusammengesetzte Wahrscheinlichkeit gibt dir das mathematische Gerüst, um mehrere Ereignisse zusammen zu behandeln. Der Schlüssel liegt darin, zu erkennen, ob du es mit UND-Szenarien (Multiplikationsregel) oder ODER-Szenarien (Additionsregel) zu tun hast und ob deine Ereignisse unabhängig oder abhängig voneinander sind. Diese Unterschiede bestimmen, welche Formel du verwenden wirst.

Mit der Zeit wirst du ein Gespür für diese Probleme entwickeln. In der Praxis werden in der Datenwissenschaft (von A/B-Tests bis hin zur Risikomodellierung) genau dieselben Prinzipien angewendet. Fang mit einfachen Beispielen an, arbeite dich Schritt für Schritt durch die Logik und baue dein Selbstvertrauen mit immer komplexeren Szenarien auf.