Probabilidade composta: Definição, regras e exemplos

Você está jogando dois dados em um jogo de tabuleiro. Quais são as chances de você tirar um seis em ambos? Ou talvez você esteja analisando dados de clientes e precise saber a probabilidade de um usuário clicar em um anúncio ou fazer uma compra.

Esses cenários envolvem probabilidade composta, que calcula a chance de vários eventos acontecerem, seja juntos ou separados. Se isso parecer confuso, não se preocupe: Vou deixar as ideias fáceis de entender com exemplos claros.

O que é probabilidade composta?

A probabilidade composta calcula a chance de dois ou mais eventos acontecerem. A probabilidade simples foca em um único evento (como jogar uma moeda), mas a probabilidade composta lida com situações em que várias coisas podem acontecer.

Nas estatísticas formais, esses cenários têm nomes específicos: o cenário AND é a probabilidade conjunta (a chance de ambos os eventos acontecerem juntos) e o cenário OR é a união (a chance de pelo menos um evento acontecer).

Pense na probabilidade composta como um termo geral fácil de entender para iniciantes, que ajuda você a aprender os dois tipos de cálculos antes de mergulhar nesses termos mais técnicos.

Tipos de eventos de probabilidade composta

A diferença entre AND e OR mostra qual fórmula usar, mas tem outra relação entre os eventos que muda como essas fórmulas funcionam. Antes de calcular probabilidades compostas com precisão, você precisa entender como os eventos se relacionam entre si. Especificamente, se um evento influencia o outro.

Eventos independentes

Dois eventos são independentes quando um não afeta o outro. Jogue uma moeda e depois um dado. Acertar cabeças não muda suas chances de rolar um quatro. Cada evento tem sua própria probabilidade, que permanece constante.

Exemplos clássicos incluem jogar vários dados, jogar várias moedas ou comprar cartas com reposição (colocando cada carta de volta antes da próxima compra). Na ciência de dados, você vai ver independência ao analisar sessões de usuários separadas ou grupos de testes A/B não relacionados.

Eventos dependentes

Os eventos são dependentes quando o primeiro evento altera a probabilidade do segundo. Pega uma carta do baralho e depois pega outra sem devolver a primeira. A segunda rodada tem chances diferentes porque a composição do baralho mudou.

Você vai ver eventos dependentes quando fizer amostragens sem reposição, em processos de decisão sequenciais ou quando os eventos estiverem ligados causalmente. A chance de uma segunda compra depende se o cliente fez uma primeira compra. Essa dependência afeta diretamente seus cálculos.

Regras para calcular a probabilidade composta

Agora que você entende as relações entre os eventos, podemos abordar os cálculos propriamente ditos.

A independência ou dependência que você acabou de aprender determina diretamente qual versão da fórmula você vai usar. O jeito de calcular depende se você está lidando com cenários AND ou OR e, dentro desses cenários, se seus eventos são independentes ou dependentes.

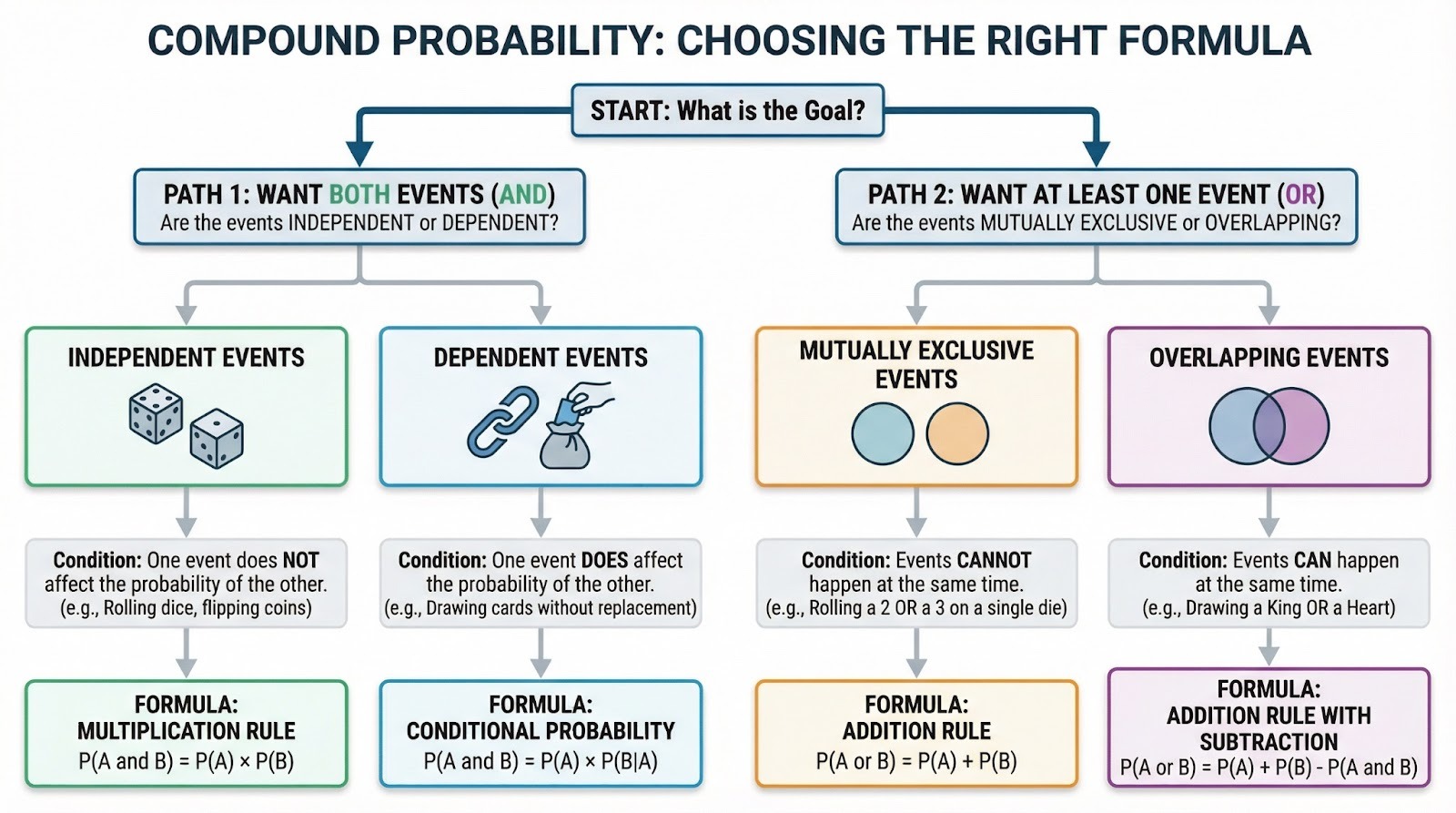
Fluxograma de decisão para escolher a fórmula correta de probabilidade composta. Imagem do autor.

A regra da multiplicação

A regra de multiplicação lida com cenários AND (quando você quer que os dois eventos ocorram). Para eventos independentes, multiplique suas probabilidades individuais: P(A ∩ B) = P(A) × P(B). Jogar um quatro E tirar cara? Isso é (1/6) × (1/2) = 1/12.

Para eventos dependentes, você vai precisar da probabilidade condicional: P(A ∩ B) = P(A) × P(B|A). Isso quer dizer “a probabilidade de A vezes a probabilidade de B, já que A aconteceu”. Tirar dois ases sem substituir? O primeiro ás é 4/52, mas o segundo ás agora é 3/51 porque você está tirando cartas de um baralho menor. Multiplique-os: (4/52) × (3/51) = 1/221.

A regra da adição (quando os eventos se sobrepõem)

A regra de adição lida com cenários OR (quando você quer que pelo menos um evento ocorra). Se os eventos não puderem acontecer ao mesmo tempo (mutuamente exclusivos), basta adicionar: P(A ou B) = P(A) + P(B). Jogar um dois OU um três em um dado significa 1/6 + 1/6 = 1/3.

Quando os eventos podem se sobrepor, você precisa subtrair a interseção para evitar a contagem dupla: P(A ou B) = P(A) + P(B) - P(A ∩ B). Tirar um rei OU um coração de um baralho? Tem 4 reis e 13 copas, mas o rei de copas conta duas vezes, então: 4/52 + 13/52 - 1/52 = 16/52.

Exemplos passo a passo de probabilidade composta

Vamos ver exemplos concretos pra entender como essas regras funcionam. Probabilidade composta é um termo geral que abrange cenários de eventos independentes e dependentes.

Exemplo com eventos independentes

Você joga uma moeda justa duas vezes. Qual é a chance de sair cara nas duas vezes? Como os lançamentos da moeda são independentes, cada lançamento tem probabilidade de 1/2. Usando a regra da multiplicação: P(Cara no lançamento 1 E Cara no lançamento 2) = 1/2 × 1/2 = 1/4. Tem 25% de chance de sair duas caras seguidas.

Exemplo com eventos dependentes

Um saco tem 5 bolinhas azuis e 3 bolinhas vermelhas. Você pega duas bolinhas de gude sem devolvê-las. Qual é a chance de os dois serem azuis? O primeiro sorteio tem probabilidade de 5/8. Depois de tirar uma bola azul, só ficam 4 bolas azuis num saco com 7, então P(Azul na segunda retirada | Azul na primeira) = 4/7. Então: P(Ambos azuis) = 5/8 × 4/7 = 20/56 = 5/14, mais ou menos 35,7%.

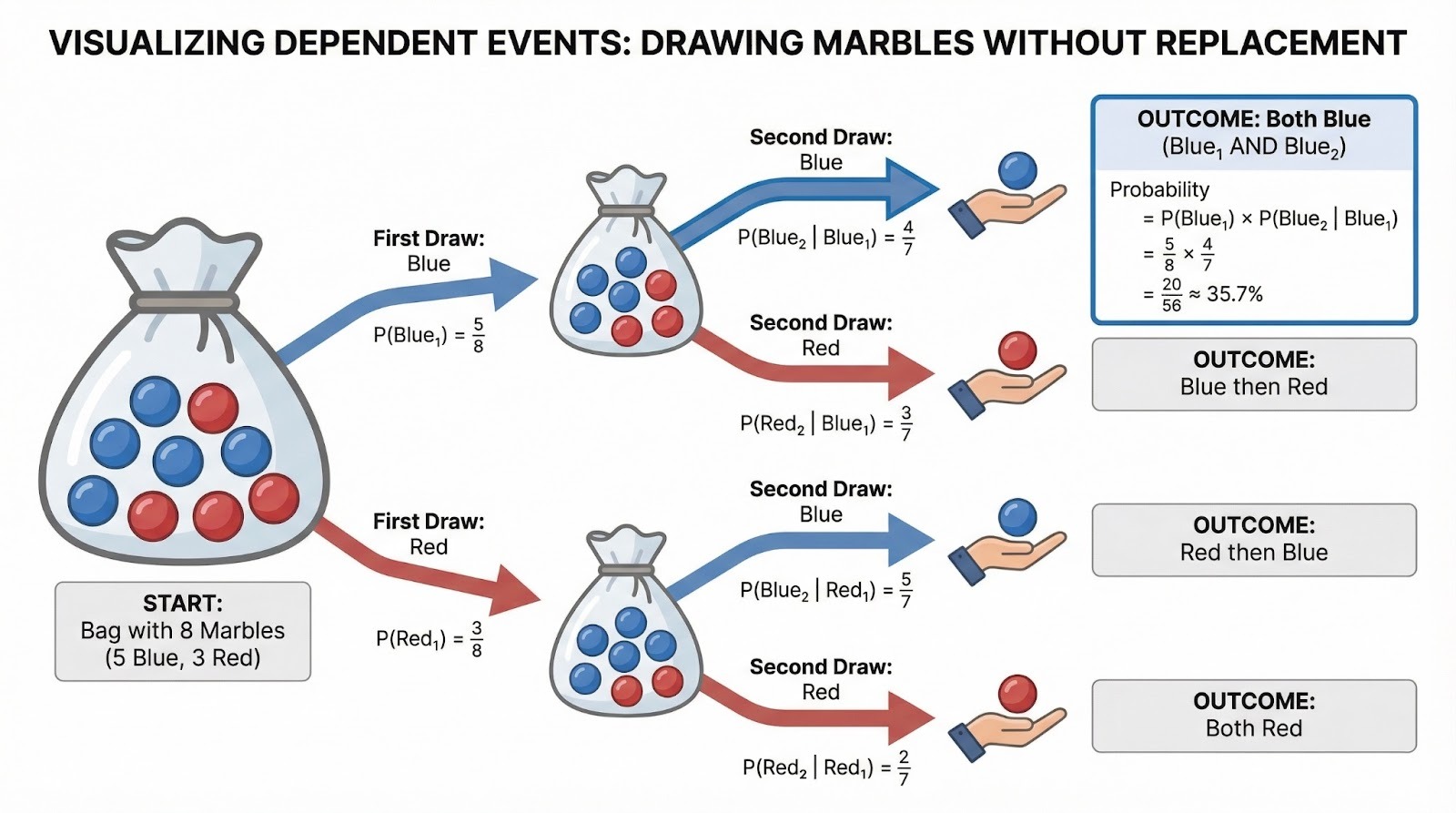
Diagrama em árvore que mostra eventos dependentes quando se tira bolinhas de gude sem recolocá-las. Imagem do autor.

Exemplo envolvendo “E” vs “OU”

É importante ler com atenção aqui. Um dado padrão é lançado. Qual é a chance de tirar um número menor que 3 OU um número par? Números menores que 3: {1, 2}. Números pares: {2, 4, 6}. Esses se sobrepõem em 2, então não dá pra simplesmente somar. Usando a regra da adição: P(Menos de 3) = 2/6, P(Par) = 3/6, P(Ambos) = 1/6. Então: 2/6 + 3/6 - 1/6 = 4/6 = 2/3.

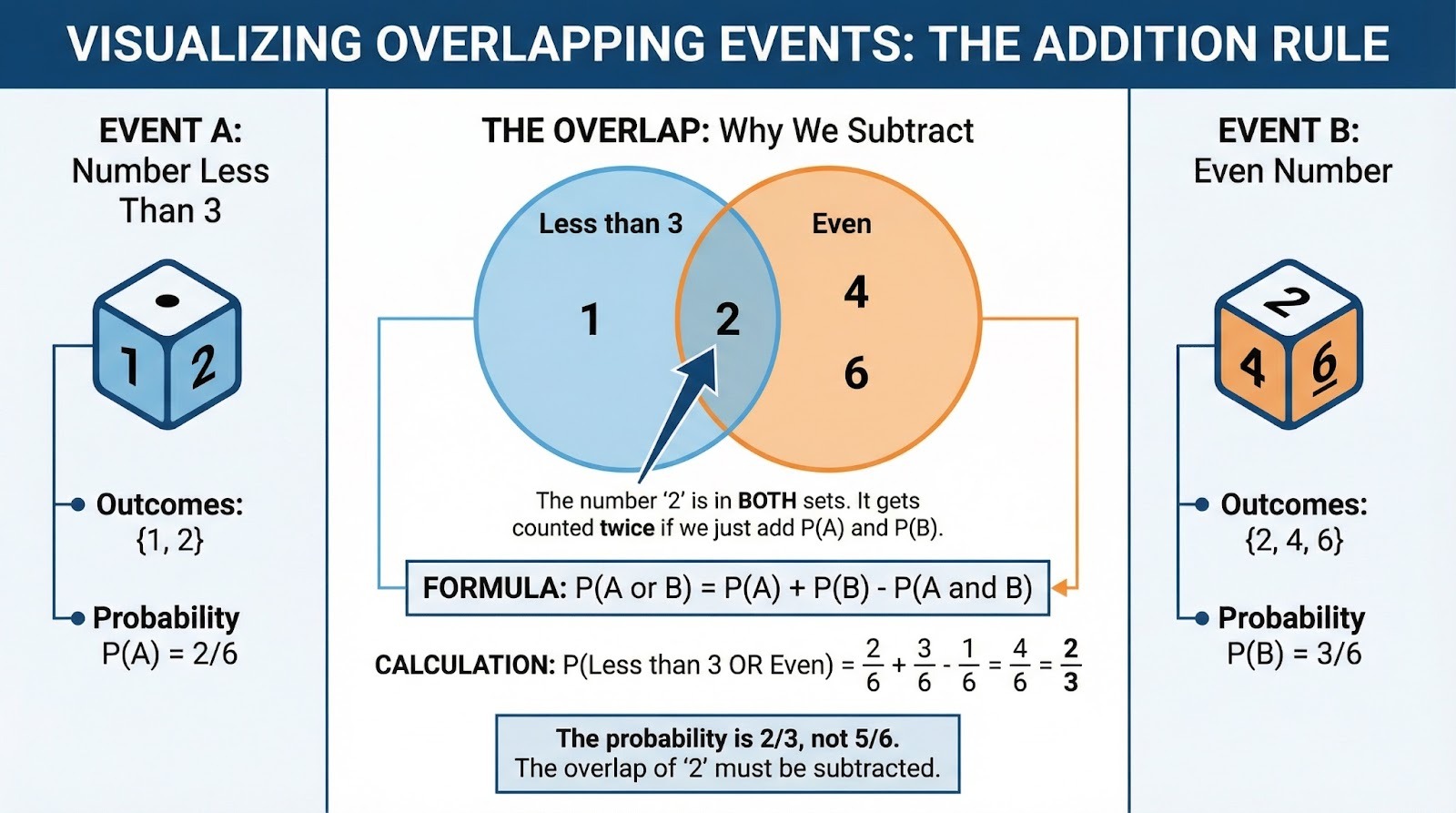
Diagrama de Venn mostrando eventos que se sobrepõem. Imagem do autor.

Observe como a palavra “ou” indica que precisamos de adição, enquanto “e” indicaria multiplicação. A linguagem usada nas questões de probabilidade indica qual regra você deve aplicar.

Erros de probabilidade composta

Tratar eventos dependentes como independentes é o erro mais comum. Se você tirar cartas sem reposição, mas multiplicar as probabilidades como se o baralho não mudasse, sua resposta vai estar errada. Pergunte sempre: o primeiro evento muda as condições para o segundo?

A soma de probabilidades quando é preciso multiplicar rola quando as pessoas confundem “e” com “ou”. Se uma questão perguntar pela probabilidade do evento A E do evento B, você multiplica (supondo independência ou usando probabilidade condicional). Adicionar dá um cenário completamente diferente.

Interpretar mal “e” versus “ou” causa confusão porque a linguagem cotidiana é menos precisa do que a linguagem matemática. “Quais são as chances de chover ou nevar amanhã?” quer dizer pelo menos uma das duas, não as duas (isso é adição). “Quais são as chances de chover e nevar amanhã?” significa que ambos podem acontecer (isso é multiplicação).

Esquecer de ajustar as probabilidades depois que um resultado acontece aparece em cenários sequenciais. Depois de tirar uma carta, o baralho tem 51 cartas, não 52. Depois que um cliente vai embora, você tem um a menos na sua amostra. Atualize suas probabilidades a cada etapa.

Como a probabilidade composta aparece

Nos jogos de azar, os cassinos usam a probabilidade composta para calcular a vantagem da casa. Entender a chance de vários resultados legais ajuda os jogadores a tomarem decisões de aposta mais informadas (mesmo que a casa sempre tenha uma vantagem matemática embutida). A análise de risco nos negócios e nas finanças depende muito da probabilidade composta. Qual é a chance de rolar uma queda no mercado E um aumento nas taxas de juros? Esses cenários compostos ajudam as empresas a se protegerem contra vários fatores de risco que podem acontecer ao mesmo tempo.

Os processos de controle de qualidade usam a probabilidade composta para avaliar a chance de defeitos. Se duas etapas de fabricação tiverem cada uma uma taxa de defeito de 2%, a probabilidade composta indica a taxa de defeito geral para os produtos que passam por ambas as etapas. Os exames médicos juntam vários resultados de testes usando probabilidade composta. Um paciente pode fazer vários exames diagnósticos, e os médicos precisam saber a probabilidade da doença com base em todos os resultados dos exames juntos, não só em um exame isolado.

Nosso curso Fundamentos de Probabilidade em Python aborda aplicações práticas comoessas em profundidade.

Probabilidade composta vs. Probabilidade Condicional

A probabilidade condicional pergunta: Considerando que B aconteceu, qual é a chance de A ter acontecido? Você estáatualizando sua estimativa de probabilidade com base em novas informações. A probabilidade composta pergunta: Qual é a chance de vários eventos acontecerem juntos?

Eles se conectam ao calcular a probabilidade composta para eventos dependentes. Você usa a probabilidade condicional na sua regra de multiplicação. P(A ∩ B) = P(A) × P(B|A) mostra essa relação de forma bem clara. A probabilidade condicional P(B|A) ajuda a calcular a probabilidade composta de A e B.

Pense nisso dessa forma. A probabilidade condicional é uma ferramenta que você usa nos cálculos de probabilidade composta. Quando os eventos são dependentes, não dá pra calcular probabilidades compostas sem pensar em como um evento afeta o outro, e é exatamente isso que a probabilidade condicional mede.

Dicas práticas para resolver problemas de probabilidade composta

Comece identificando quantos eventos estão envolvidos e se eles são independentes ou dependentes. Procure pistas: o problema fala em substituição? Um evento muda as condições para o próximo? Eventos independentes mantêm suas probabilidades constantes, enquanto eventos dependentes exigem que você atualize as probabilidades após cada evento.

Traduza “e” ou “ou” com cuidado, porque essas palavras determinam toda a sua abordagem. Anote o que você sabe antes de calcular. Liste as probabilidades individuais, identifique quaisquer probabilidades condicionais e faça um esboço rápido se estiver trabalhando com eventos sequenciais. Esse trabalho de preparação evita erros quando você começa a fazer os cálculos.

Dá uma olhada nos seus resultados pra ver se tá tudo certo. As probabilidades têm que ficar entre 0 e 1. Se você estiver multiplicando probabilidades, sua resposta deve ser menor do que a menor probabilidade individual. Se algo parecer errado, dê uma olhada no seu trabalho antes de passar para a ala d. Nosso curso Probability Puzzles in R oferece prática com essas estratégias de resolução de problemas.

Conclusão

A probabilidade composta dá a estrutura matemática pra lidar com vários eventos juntos. O segredo é saber se você está lidando com cenários AND (regra da multiplicação) ou OR (regra da adição) e se seus eventos são independentes ou dependentes. Essas diferenças determinam qual fórmula você vai usar.

Com a prática, você vai pegar o jeito pra resolver esses problemas. As aplicações reais na ciência de dados (desde testes A/B até modelagem de risco) usam esses mesmos princípios. Comece com exemplos simples, trabalhe a lógica passo a passo e ganhe confiança com cenários cada vez mais complexos.