Clustering hiérarchique en R

Opérations de prétraitement pour le regroupement

Il y a quelques points que vous devez prendre en compte avant de commencer.

• Mise à l'échelle

Il est impératif de normaliser l'échelle des valeurs des caractéristiques avant d'entamer le processus de regroupement. En effet, les valeurs des caractéristiques de chaque observation sont représentées sous forme de coordonnées dans un espace à n dimensions (n étant le nombre de caractéristiques), puis les distances entre ces coordonnées sont calculées. Si ces coordonnées ne sont pas normalisées, cela peut conduire à des résultats erronés.

Par exemple, supposons que vous disposiez de données sur la taille et le poids de trois personnes : A (1m80, 75kg), B (1m80, 77kg), C (1m80, 75kg). Si vous représentez ces caractéristiques dans un système de coordonnées à deux dimensions, la taille et le poids, et que vous calculez la distance euclidienne qui les sépare, la distance entre les paires suivantes sera la suivante :

A-B : 2 unités

A-C : 2 unités

La métrique de la distance indique que les paires A-B et A-C sont similaires, mais en réalité, elles ne le sont clairement pas ! La paire A-B est plus similaire que la paire A-C. Il est donc important de commencer par mettre ces valeurs à l'échelle, puis de calculer la distance.

Il existe plusieurs façons de normaliser les valeurs des caractéristiques. Vous pouvez envisager de normaliser l'échelle complète de toutes les valeurs des caractéristiques (x(i)) entre [0,1] (normalisation min-max) en appliquant la transformation suivante :

x(s) = x(i) - min(x)/(max(x) - min (x)) $ x(s) = x(i) - min(x)/(max(x) - min (x))

Vous pouvez utiliser la fonction normalize() pour cela ou vous pouvez écrire votre propre fonction comme :

standardize <- function(x){(x-min(x))/(max(x)-min(x))}

Un autre type de mise à l'échelle peut être obtenu par la transformation suivante :

x(s) = x(i)-moyenne(x) / sd(x) $ x(s) = x(i)-moyenne(x) / sd(x) $

Où sd(x) est l'écart-type des valeurs des caractéristiques. Ainsi, votre distribution de valeurs de caractéristiques aura une moyenne de 0 et un écart type de 1. Vous pouvez y parvenir à l'aide de la fonction scale() dans R.

• Imputation des valeurs manquantes

Il est également important de traiter au préalable les valeurs manquantes/nulles/inf dans votre ensemble de données. Il y a plusieurs façons de traiter ces valeurs, soit en les supprimant, soit en les imputant avec la moyenne, la médiane, le mode ou en utilisant des techniques de régression avancées. R dispose de nombreux paquets et fonctions pour traiter les imputations de valeurs manquantes comme impute(), Amelia, Mice, Hmisc etc. Vous pouvez en savoir plus sur Amelia dans ce tutoriel.

Algorithme de regroupement hiérarchique

L'opération clé du regroupement agglomératif hiérarchique consiste à combiner de manière répétée les deux grappes les plus proches en une grappe plus grande. Il faut d'abord répondre à trois questions clés :

• Comment représenter une grappe de plusieurs points ?
• Comment déterminez-vous la "proximité" des grappes ?
• Quand cessez-vous de combiner les grappes ?

Nous espérons qu'à la fin de ce tutoriel, vous serez en mesure de répondre à toutes ces questions. Avant d'appliquer la classification hiérarchique, examinons son fonctionnement :

1. Il commence par calculer la distance entre chaque paire de points d'observation et la stocke dans une matrice de distance.
2. Il place ensuite chaque point dans son propre groupe.
3. Il commence ensuite à fusionner les paires de points les plus proches en se basant sur les distances de la matrice des distances, ce qui a pour effet de réduire le nombre de grappes de 1.
4. Il recalcule ensuite la distance entre le nouveau groupe et les anciens et les stocke dans une nouvelle matrice de distance.
5. Enfin, il répète les étapes 2 et 3 jusqu'à ce que toutes les grappes soient fusionnées en une seule.

Il existe plusieurs façons de mesurer la distance entre les grappes afin de décider des règles de regroupement, et elles sont souvent appelées méthodes de liaison. Voici quelques-unes des méthodes de couplage les plus courantes :

• Liaison complète : calcule la distance maximale entre les grappes avant de les fusionner.

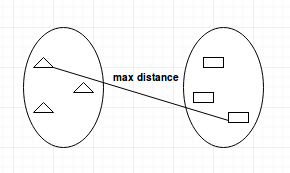
• Single-linkage : calcule la distance minimale entre les grappes avant de les fusionner. Ce lien peut être utilisé pour détecter des valeurs élevées dans votre ensemble de données, qui peuvent être des valeurs aberrantes, car elles seront fusionnées à la fin.

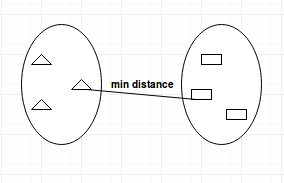
• Liaison moyenne : calcule la distance moyenne entre les grappes avant de les fusionner.

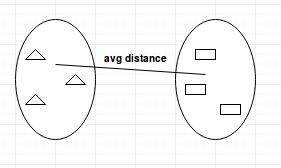
• Lien avec le centroïde : trouve le centroïde du groupe 1 et le centroïde du groupe 2, puis calcule la distance entre les deux avant de les fusionner.

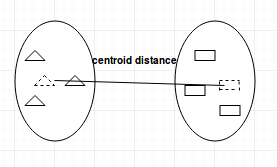
Le choix de la méthode de liaison dépend entièrement de vous et il n'existe pas de méthode stricte et rapide qui vous donnera toujours de bons résultats. Différentes méthodes de couplage aboutissent à des groupes différents.

Dendrogrammes

Dans le cas du regroupement hiérarchique, vous classez les objets dans une hiérarchie semblable à un diagramme arborescent appelé dendrogramme. La distance de séparation ou de fusion (appelée hauteur) est indiquée sur l'axe des ordonnées du dendrogramme ci-dessous.

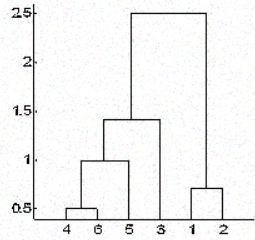
Dans la figure ci-dessus, les points 4 et 6 sont d'abord combinés en un seul groupe, dit groupe 1, car ils étaient les plus proches en distance, suivis par les points 1 et 2, dit groupe 2. Ensuite, 5 a été fusionné dans le même groupe 1, suivi de 3, ce qui a donné deux groupes. Enfin, les deux groupes sont fusionnés en un seul groupe et le processus de regroupement s'arrête là.

Une question qui vous intrigue peut-être maintenant est la suivante : comment décidez-vous d'arrêter de fusionner les grappes ? Cela dépend de la connaissance du domaine que vous avez des données. Par exemple, si vous regroupez des joueurs de football sur un terrain en fonction de leur position sur le terrain, qui représentera leurs coordonnées pour le calcul de la distance, vous savez déjà que vous ne devez obtenir que deux groupes, car il ne peut y avoir que deux équipes lors d'un match de football.

Mais il arrive aussi que vous ne disposiez pas de ces informations. Dans ce cas, vous pouvez utiliser les résultats du dendrogramme pour déterminer approximativement le nombre de groupes. Vous coupez l'arbre du dendrogramme avec une ligne horizontale à une hauteur où la ligne peut parcourir la distance maximale vers le haut et vers le bas sans croiser le point de fusion. Dans le cas ci-dessus, elle se situe entre les hauteurs 1,5 et 2,5, comme indiqué :

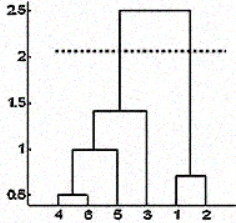
Si vous effectuez la coupe comme indiqué, vous n'obtiendrez que deux grappes.

Notez qu'il n'est pas nécessaire de faire une coupe uniquement à ces endroits, vous pouvez choisir n'importe quel point comme point de coupe en fonction du nombre de grappes que vous souhaitez. Par exemple, la coupe inférieure à 1,5 et supérieure à 1 vous donnera 3 grappes.

Notez qu' il ne s'agit pas d'une règle absolue pour déterminer le nombre de grappes. Vous pouvez également envisager des graphiques tels que le graphique de Silhouette, le graphique en coude, ou certaines mesures numériques telles que l'indice de Dunn, le gamma de Hubert, etc. qui montre la variation de l'erreur avec le nombre de grappes (k), et vous choisissez la valeur de k pour laquelle l'erreur est la plus faible.

Mesurer la qualité des grappes d'entreprises

L'analyse des résultats est peut-être la partie la plus importante de toute tâche d'apprentissage non supervisé. Après avoir effectué le regroupement en utilisant n'importe quel algorithme et n'importe quel ensemble de paramètres, vous devez vous assurer que vous l'avez fait correctement. Mais comment le déterminer ?

Il existe de nombreuses mesures pour y parvenir, la plus populaire étant sans doute le site Dunn's Index. L'indice de Dunn est le rapport entre les distances minimales entre les grappes et le diamètre maximal à l'intérieur des grappes. Le diamètre d'une grappe est la distance entre ses deux points les plus éloignés. Pour obtenir des grappes bien séparées et compactes, vous devez viser un indice de Dunn plus élevé.

Le regroupement hiérarchique en action

Vous allez maintenant appliquer les connaissances que vous avez acquises pour résoudre un problème du monde réel.

Vous appliquerez la classification hiérarchique à l'ensemble de données seeds. Cet ensemble de données consiste en des mesures des propriétés géométriques de grains appartenant à trois variétés différentes de blé : Kama, Rosa et Canadian. Il comporte des variables qui décrivent les propriétés des graines, telles que la surface, le périmètre, le coefficient d'asymétrie, etc. Il y a 70 observations pour chaque variété de blé. Vous pouvez trouver les détails de l'ensemble de données ici.

Commencez par importer l'ensemble de données dans un dataframe à l'aide de la fonction read.csv().

Notez que le fichier n'a pas d'en-tête et qu'il est séparé par des tabulations. Pour maintenir la reproductibilité des résultats, vous devez utiliser la fonction set.seed().

set.seed(786)
file_loc <- 'seeds.txt'
seeds_df <- read.csv(file_loc,sep = '\t',header = FALSE)

Puisque l'ensemble de données n'a pas de nom de colonne, vous devez donner vous-même le nom des colonnes à partir de la description des données.

feature_name <- c('area','perimeter','compactness','length.of.kernel','width.of.kernal','asymmetry.coefficient','length.of.kernel.groove','type.of.seed')
colnames(seeds_df) <- feature_name

Il est conseillé de rassembler quelques informations de base utiles sur l'ensemble de données, telles que ses dimensions, les types de données et leur distribution, le nombre de NA, etc. Pour ce faire, vous utiliserez les fonctions str(), summary() et is.na() dans R.

str(seeds_df)
summary(seeds_df)
any(is.na(seeds_df))

Notez que toutes les colonnes de cet ensemble de données sont des valeurs numériques. Il n'y a pas de valeurs manquantes dans cet ensemble de données que vous devez nettoyer avant de procéder au regroupement. Mais les échelles des caractéristiques sont différentes et vous devez les normaliser. De plus, les données sont étiquetées et vous savez déjà quelle observation correspond à quelle variété de blé.

Vous allez maintenant stocker les étiquettes dans une variable distincte et exclure la colonne type.of.seed de votre ensemble de données afin de procéder au regroupement. Plus tard, vous utiliserez les vraies étiquettes pour vérifier la qualité de votre regroupement.

seeds_label <- seeds_df$type.of.seed
seeds_df$type.of.seed <- NULL
str(seeds_df)

Comme vous pouvez le constater, vous avez supprimé la colonne "true label" de votre ensemble de données.

Vous allez maintenant utiliser la fonction scale() de R pour mettre à l'échelle toutes les valeurs de vos colonnes.

seeds_df_sc <- as.data.frame(scale(seeds_df))
summary(seeds_df_sc)

Remarquez que la moyenne de toutes les colonnes est de 0 et que l'écart-type est de 1. Maintenant que vous avez prétraité vos données, il est temps de construire la matrice de distance. Comme toutes les valeurs sont des valeurs numériques continues, vous utiliserez la méthode de la distance euclidean.

dist_mat <- dist(seeds_df_sc, method = 'euclidean')

À ce stade, vous devez décider de la méthode de couplage que vous souhaitez utiliser et procéder au regroupement hiérarchique. Vous pouvez essayer toutes sortes de méthodes de liaison et décider plus tard laquelle est la plus performante. Ici, vous procéderez à la méthode de liaison average.

Vous construirez votre dendrogramme en traçant l'objet cluster hiérarchique que vous construirez avec hclust(). Vous pouvez spécifier la méthode de liaison via l'argument method.

hclust_avg <- hclust(dist_mat, method = 'average')
plot(hclust_avg)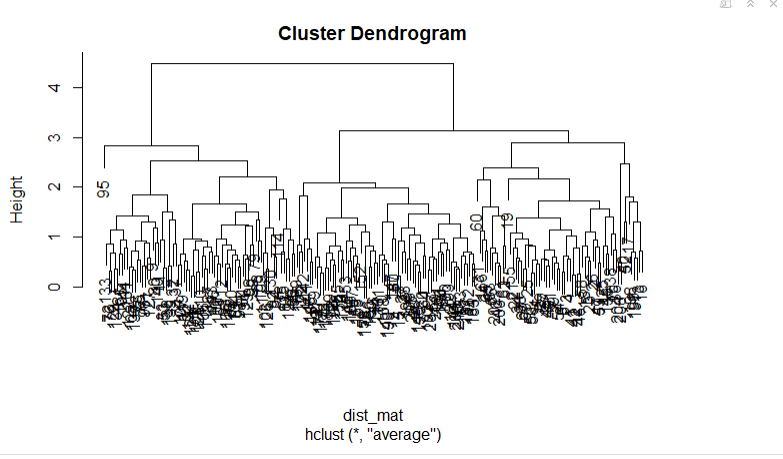

Remarquez comment le dendrogramme est construit et comment chaque point de données fusionne finalement en un seul groupe avec la hauteur (distance) indiquée sur l'axe des ordonnées.

Ensuite, vous pouvez couper le dendrogramme afin de créer le nombre de groupes souhaité. Puisque dans ce cas vous savez déjà qu'il ne peut y avoir que trois types de blé, vous choisirez le nombre de clusters k = 3, ou comme vous pouvez le voir dans le dendrogramme h = 3 vous obtenez trois clusters. Vous utiliserez la fonction cutree() de R pour couper l'arbre avec hclust_avg comme paramètre et l'autre paramètre comme h = 3 ou k = 3.

cut_avg <- cutree(hclust_avg, k = 3)

Si vous souhaitez voir les groupes sur le dendrogramme, vous pouvez utiliser la fonction abline() de R pour tracer la ligne de coupe et superposer des compartiments rectangulaires pour chaque groupe sur l'arbre avec la fonction rect.hclust(), comme le montre le code suivant :

plot(hclust_avg)
rect.hclust(hclust_avg , k = 3, border = 2:6)
abline(h = 3, col = 'red')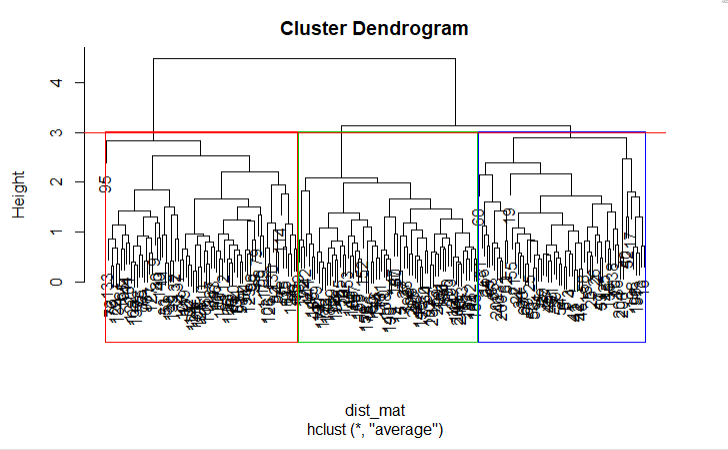

Vous pouvez maintenant voir les trois groupes enfermés dans trois boîtes de couleurs différentes. Vous pouvez également utiliser la fonction color_branches() de la bibliothèque dendextend pour visualiser votre arbre avec des branches de différentes couleurs.

Rappelez-vous que vous pouvez installer un paquetage dans R en utilisant la commande install.packages('package_name', dependencies = TRUE).

suppressPackageStartupMessages(library(dendextend))
avg_dend_obj <- as.dendrogram(hclust_avg)
avg_col_dend <- color_branches(avg_dend_obj, h = 3)
plot(avg_col_dend)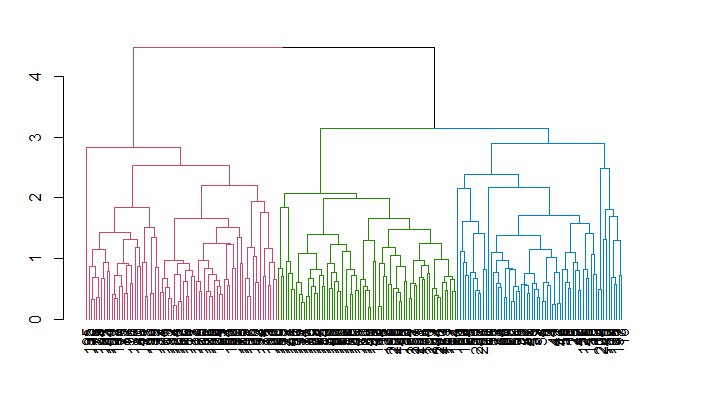

Vous allez maintenant ajouter les résultats des grappes obtenus dans le DataFrame original sous le nom de colonne cluster avec mutate(), du package dplyr et compter combien d'observations ont été assignées à chaque grappe avec la fonction count().

suppressPackageStartupMessages(library(dplyr))
seeds_df_cl <- mutate(seeds_df, cluster = cut_avg)
count(seeds_df_cl,cluster)

Vous pourrez voir combien d'observations ont été attribuées à chaque groupe. Notez qu'en réalité, à partir des données étiquetées, vous disposez de 70 observations pour chaque variété de blé.

Il est courant d'évaluer la tendance entre deux caractéristiques sur la base du regroupement que vous avez effectué afin d'extraire des informations plus utiles des données par regroupement. À titre d'exercice, vous pouvez analyser la tendance entre perimeter et area pour le blé, par groupe, à l'aide du paquet ggplot2.

suppressPackageStartupMessages(library(ggplot2))
ggplot(seeds_df_cl, aes(x=area, y = perimeter, color = factor(cluster))) + geom_point()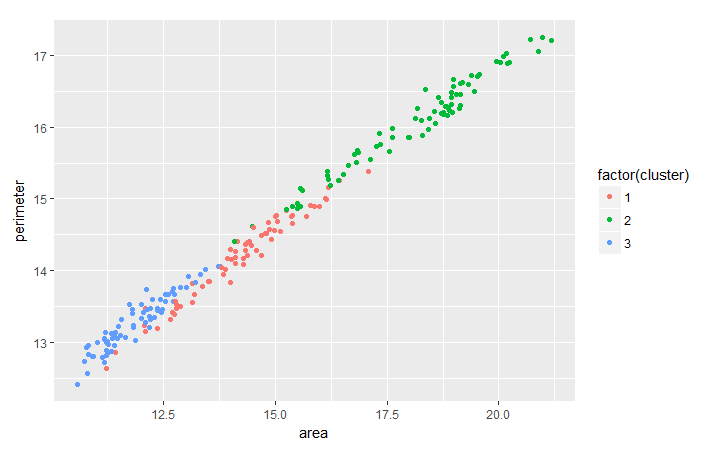

Remarquez que pour toutes les variétés de blé, il semble y avoir une relation linéaire entre leur périmètre et leur surface.

Comme vous disposez déjà des vraies étiquettes pour cet ensemble de données, vous pouvez également envisager de vérifier les résultats de votre regroupement à l'aide de la fonction table().

table(seeds_df_cl$cluster,seeds_label)

Si vous regardez le tableau qui a été généré, vous voyez clairement trois groupes avec 55 éléments ou plus. Dans l'ensemble, vous pouvez dire que vos grappes représentent de manière adéquate les différents types de semences car, à l'origine, vous disposiez de 70 observations pour chaque variété de blé. Les groupes les plus grands représentent la correspondance entre les groupes et les types réels.

Notez que dans de nombreux cas, vous ne disposez pas des véritables étiquettes. Dans ce cas, comme nous l'avons déjà mentionné, vous pouvez opter pour d'autres mesures telles que la maximisation de l'indice de Dunn. Vous pouvez calculer l'indice de Dunn en utilisant la fonction dunn() de la bibliothèque clValid. Vous pouvez également envisager de procéder à une validation croisée des résultats en créant des ensembles de formation et de test, comme vous le faites pour tout autre algorithme d'apprentissage automatique, puis en procédant au regroupement lorsque vous disposez des véritables étiquettes.

Comparaison avec l'algorithme de regroupement K-Means

Vous avez peut-être entendu parler de l'algorithme de regroupement k-means ; si ce n'est pas le cas, jetez un coup d'œil à ce didacticiel. Il existe de nombreuses différences fondamentales entre les deux algorithmes, même si l'un d'entre eux peut être plus performant que l'autre dans différents cas. Voici quelques-unes des différences :

• Distance utilisée : Le regroupement hiérarchique peut virtuellement traiter n'importe quelle métrique de distance alors que les k-moyennes reposent sur les distances euclidiennes.
• Stabilité des résultats : la méthode k-means nécessite une étape aléatoire lors de son initialisation, qui peut donner des résultats différents si le processus est réexécuté. Ce n'est pas le cas dans le cadre d'un regroupement hiérarchique.
• Nombre de groupes : Alors que vous pouvez utiliser les diagrammes en coude, les diagrammes de Silhouette, etc. pour déterminer le bon nombre de grappes dans le cadre de la méthode k-means, la méthode hiérarchique peut également utiliser tous ces éléments, mais avec l'avantage supplémentaire de tirer parti du dendrogramme pour la même raison.
• Complexité de calcul : La méthode K-means est moins coûteuse en termes de calcul que le regroupement hiérarchique et peut être exécutée sur de grands ensembles de données dans un délai raisonnable, ce qui est la principale raison pour laquelle la méthode k-means est plus populaire.

Conclusion

Félicitations ! Vous avez atteint la fin de ce tutoriel. Vous avez appris comment prétraiter vos données, les bases du clustering hiérarchique, les métriques de distance et les méthodes de liaison sur lesquelles il fonctionne, ainsi que son utilisation dans R. Vous savez également en quoi le clustering hiérarchique diffère de l'algorithme des k-moyennes. Bravo ! Mais il reste toujours beaucoup à apprendre. Je vous suggère de jeter un coup d'œil à notre cours sur l 'apprentissage non supervisé en R.