Agrupación jerárquica en R

En este tutorial, aprenderá a realizar clustering jerárquico en un conjunto de datos en R. Si desea aprender sobre clustering jerárquico en Python, consulte nuestro artículo separado. 

Introducción

Como su propio nombre indica, los algoritmos de Clustering agrupan un conjunto de puntos de datos en subconjuntos o clusters. El objetivo de los algoritmos es crear agrupaciones que sean coherentes internamente, pero claramente diferentes entre sí externamente. En otras palabras, las entidades de un clúster deben ser lo más parecidas posible y las entidades de un clúster deben ser lo menos parecidas posible a las entidades de otro.

En términos generales, existen dos formas de agrupar puntos de datos basadas en la estructura y el funcionamiento algorítmicos, a saber, la aglomerativa y la divisiva.

• Aglomerativo: Un enfoque aglomerativo comienza con cada observación en un conglomerado distinto (singleton) y fusiona sucesivamente los conglomerados hasta que se cumple un criterio de parada.
• Divisivo: Un método divisivo comienza con todos los patrones de un mismo conglomerado y realiza la división hasta que se cumple un criterio de parada.

En este tutorial se va a centrar en el enfoque aglomerativo o ascendente, en el que se empieza con cada punto de datos como su propio conglomerado y luego se combinan los conglomerados basándose en alguna medida de similitud. La idea también puede adaptarse fácilmente a los métodos de división.

La similitud entre los conglomerados suele calcularse a partir de medidas de disimilitud como la distancia euclidiana entre dos conglomerados. Por tanto, cuanto mayor sea la distancia entre dos conglomerados, mejor.

Hay muchas métricas de distancia que se pueden considerar para calcular la medida de disimilitud, y la elección depende del tipo de datos del conjunto de datos. Por ejemplo, si tiene valores numéricos continuos en su conjunto de datos puede utilizar la distancia euclidean, si los datos son binarios puede considerar la distancia Jaccard (útil cuando se trata de datos categóricos para la agrupación después de haber aplicado la codificación one-hot). Otras medidas de distancia son Manhattan, Minkowski, Canberra, etc.

Operaciones de preprocesamiento para la agrupación

Hay un par de cosas que debes tener en cuenta antes de empezar.

• Escala

Es imprescindible normalizar la escala de valores de las características para comenzar con el proceso de agrupación. Esto se debe a que los valores de las características de cada observación se representan como coordenadas en un espacio n-dimensional (n es el número de características) y luego se calculan las distancias entre estas coordenadas. Si estas coordenadas no se normalizan, pueden producirse resultados falsos.

Por ejemplo, supongamos que dispone de datos sobre la altura y el peso de tres personas: A (1,80 m, 75 kg), B (1,80 m, 77 kg), C (1,80 m, 75 kg). Si representas estas características en un sistema de coordenadas bidimensional, altura y peso, y calculas la distancia euclidiana entre ellas, la distancia entre los siguientes pares sería:

A-B : 2 unidades

A-C : 2 unidades

Pues bien, la métrica de la distancia dice que los pares A-B y A-C son similares, ¡pero en realidad es evidente que no lo son! El par A-B es más similar que el par A-C. De ahí que sea importante escalar primero estos valores y luego calcular la distancia.

Hay varias formas de normalizar los valores de las características, puedes considerar normalizar la escala completa de todos los valores de las características (x(i)) entre [0,1] (conocido como normalización min-max) aplicando la siguiente transformación:

$ x(s) = x(i) - min(x)/(max(x) - min (x)) $

Puede utilizar la función normalize() para esto o puedes escribir tu propia función como

standardize <- function(x){(x-min(x))/(max(x)-min(x))}

Otro tipo de escalado puede conseguirse mediante la siguiente transformación:

$ x(s) = x(i)-mean(x) / sd(x) $

Donde sd(x) es la desviación estándar de los valores de las características. Esto garantizará que su distribución de valores de características tenga una media de 0 y una desviación estándar de 1. Puede conseguirlo mediante la función scale() en R.

• Imputación de valores perdidos

También es importante tratar de antemano los valores que faltan/nulos/inf. en el conjunto de datos. Hay muchas formas de tratar estos valores, una es eliminarlos o imputarlos con la media, la mediana, la moda o utilizar algunas técnicas avanzadas de regresión. R tiene muchos paquetes y funciones para tratar las imputaciones de valores perdidos como impute(), Amelia, Mice, Hmisc etc. Puedes leer sobre Amelia en este tutorial.

Algoritmo de agrupación jerárquica

La operación clave en la agrupación jerárquica aglomerativa consiste en combinar repetidamente los dos conglomerados más cercanos en un conglomerado mayor. Primero hay que responder a tres preguntas clave:

• ¿Cómo se representa una agrupación de más de un punto?
• ¿Cómo se determina la "cercanía" de las agrupaciones?
• ¿Cuándo se deja de combinar racimos?

Esperamos que al final de este tutorial puedas responder a todas estas preguntas. Antes de aplicar la agrupación jerárquica, echemos un vistazo a su funcionamiento:

1. Comienza calculando la distancia entre cada par de puntos de observación y la almacena en una matriz de distancias.
2. A continuación, coloca cada punto en su propio clúster.
3. A continuación, empieza a fusionar los pares de puntos más cercanos basándose en las distancias de la matriz de distancias y, como resultado, el número de clusters disminuye en 1.
4. A continuación, vuelve a calcular la distancia entre el nuevo conglomerado y los antiguos y los almacena en una nueva matriz de distancias.
5. Por último, repite los pasos 2 y 3 hasta que todos los conglomerados se fusionan en uno solo.

Existen varias formas de medir la distancia entre conglomerados para decidir las reglas de agrupación, y suelen denominarse métodos de vinculación. Algunos de los métodos de vinculación más comunes son:

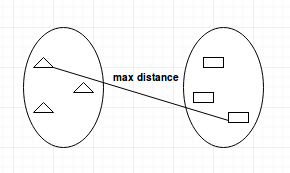
• Enlace completo: calcula la distancia máxima entre clusters antes de fusionarlos.

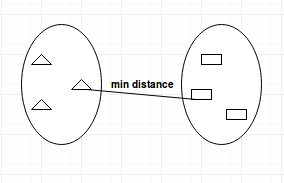
• Single-linkage: calcula la distancia mínima entre los clusters antes de fusionarlos. Esta vinculación puede utilizarse para detectar valores altos en el conjunto de datos que pueden ser valores atípicos, ya que se fusionarán al final.

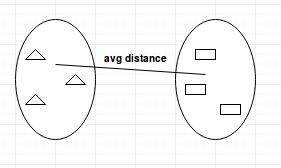
• Enlace medio: calcula la distancia media entre clusters antes de fusionarlos.

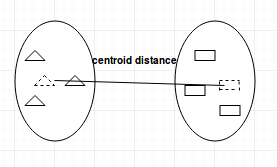
• Centroid-linkage: encuentra el centroide del cluster 1 y el centroide del cluster 2, y luego calcula la distancia entre los dos antes de fusionarlos.

La elección del método de acoplamiento depende totalmente de usted y no existe un método rígido y rápido que siempre le dé buenos resultados. Diferentes métodos de vinculación conducen a diferentes agrupaciones.

Dendrogramas

En la agrupación jerárquica, los objetos se clasifican en una jerarquía similar a un diagrama en forma de árbol, denominado dendrograma. La distancia de división o fusión (denominada altura) se muestra en el eje y del dendrograma siguiente.

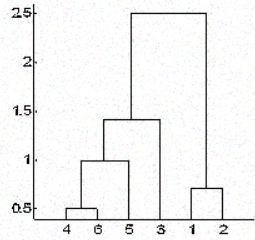
En la figura anterior, al principio 4 y 6 se combinan en un conglomerado, digamos conglomerado 1, ya que eran los más cercanos en distancia, seguidos de los puntos 1 y 2, digamos conglomerado 2. Después, 5 se fusionó en el mismo clúster 1 seguido de 3, lo que dio lugar a dos clústeres. Por último, los dos conglomerados se fusionan en un único conglomerado y aquí se detiene el proceso de agrupación.

Una pregunta que quizá ya te haya intrigado es cómo decidir cuándo dejar de fusionar las agrupaciones. Eso depende del conocimiento que se tenga de los datos. Por ejemplo, si está agrupando jugadores de fútbol en un campo basándose en sus posiciones en el campo, que representarán sus coordenadas para el cálculo de la distancia, ya sabe que debería terminar con sólo 2 grupos, ya que sólo puede haber dos equipos jugando un partido de fútbol.

Pero a veces tampoco se dispone de esa información. En tales casos, puede aprovechar los resultados del dendrograma para aproximar el número de conglomerados. Corta el árbol del dendrograma con una línea horizontal a una altura en la que la línea pueda recorrer la máxima distancia hacia arriba y hacia abajo sin intersecar el punto de fusión. En el caso anterior estaría entre las alturas 1,5 y 2,5 como se muestra:

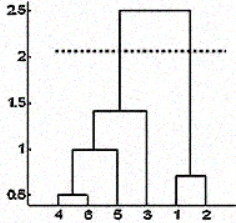
Si hace el corte como se muestra, acabará con sólo dos racimos.

Tenga en cuenta que no es necesario hacer un corte sólo en esos lugares, puede elegir cualquier punto como punto de corte en función del número de grupos que desee. Por ejemplo, el corte por debajo de 1,5 y por encima de 1 le dará 3 racimos.

Tenga en cuenta que no se trata de una regla rígida para decidir el número de grupos. También se pueden considerar gráficos como el gráfico de silueta, el gráfico de codo o algunas medidas numéricas como el índice de Dunn, la gamma de Hubert, etc., que muestran la variación del error con el número de conglomerados (k), y se elige el valor de k en el que el error es menor.

Medir la bondad de las agrupaciones

Quizá la parte más importante en cualquier tarea de aprendizaje no supervisado sea el análisis de los resultados. Después de haber realizado la agrupación utilizando cualquier algoritmo y cualquier conjunto de parámetros, debe asegurarse de que lo ha hecho correctamente. Pero, ¿cómo se determina eso?

Bueno, hay muchas medidas para hacerlo, quizás la más popular sea la Dunn's Index. El índice de Dunn es la relación entre las distancias mínimas intercluster y el diámetro máximo intracluster. El diámetro de un cúmulo es la distancia entre sus dos puntos más alejados. Para obtener racimos bien separados y compactos, debe buscar un índice de Dunn más alto.

Agrupación jerárquica en acción

Ahora aplicarás los conocimientos adquiridos para resolver un problema del mundo real.

Aplicará la agrupación jerárquica al conjunto de datos seeds. Este conjunto de datos consiste en mediciones de propiedades geométricas de granos pertenecientes a tres variedades distintas de trigo: Kama, Rosa y Canadiense. Tiene variables que describen las propiedades de las semillas como el área, el perímetro, el coeficiente de asimetría, etc. Hay 70 observaciones para cada variedad de trigo. Encontrará más información sobre el conjunto de datos aquí.

Empiece importando el conjunto de datos en un marco de datos con la función read.csv().

Tenga en cuenta que el archivo no tiene cabeceras y está separado por tabuladores. Para mantener la reproducibilidad de los resultados es necesario utilizar la función set.seed().

set.seed(786)
file_loc <- 'seeds.txt'
seeds_df <- read.csv(file_loc,sep = '\t',header = FALSE)

Dado que el conjunto de datos no tiene nombres de columnas, deberá asignarles un nombre usted mismo a partir de la descripción de los datos.

feature_name <- c('area','perimeter','compactness','length.of.kernel','width.of.kernal','asymmetry.coefficient','length.of.kernel.groove','type.of.seed')
colnames(seeds_df) <- feature_name

Es aconsejable recopilar información básica útil sobre el conjunto de datos, como sus dimensiones, tipos y distribución de datos, número de NA, etc. Para ello, utilizará las funciones str(), summary() y is.na() de R.

str(seeds_df)
summary(seeds_df)
any(is.na(seeds_df))

Tenga en cuenta que este conjunto de datos tiene todas las columnas como valores numéricos. No hay valores perdidos en este conjunto de datos que tenga que limpiar antes de la agrupación. Pero las escalas de las características son diferentes y hay que normalizarlas. Además, los datos están etiquetados y ya tiene la información sobre qué observación pertenece a qué variedad de trigo.

Ahora almacenará las etiquetas en una variable separada y excluirá la columna type.of.seed de su conjunto de datos para poder realizar la agrupación. Más tarde utilizará las etiquetas verdaderas para comprobar la calidad de su agrupación.

seeds_label <- seeds_df$type.of.seed
seeds_df$type.of.seed <- NULL
str(seeds_df)

Como podrá observar, ha eliminado la columna de la etiqueta verdadera de su conjunto de datos.

Ahora utilizará la función scale() de R para escalar todos los valores de sus columnas.

seeds_df_sc <- as.data.frame(scale(seeds_df))
summary(seeds_df_sc)

Observa que la media de todas las columnas es 0 y la desviación típica es 1. Una vez preprocesados los datos, es hora de construir la matriz de distancias. Como todos los valores aquí son valores numéricos continuos, se utilizará el método de la distancia euclidean.

dist_mat <- dist(seeds_df_sc, method = 'euclidean')

En este punto debe decidir qué método de vinculación desea utilizar y proceder a realizar la agrupación jerárquica. Puede probar todo tipo de métodos de vinculación y decidir después cuál funcionó mejor. Aquí procederá con el método de enlace average.

Construirá su dendrograma trazando el objeto cluster jerárquico que construirá con hclust(). Puede especificar el método de vinculación mediante el argumento method.

hclust_avg <- hclust(dist_mat, method = 'average')
plot(hclust_avg)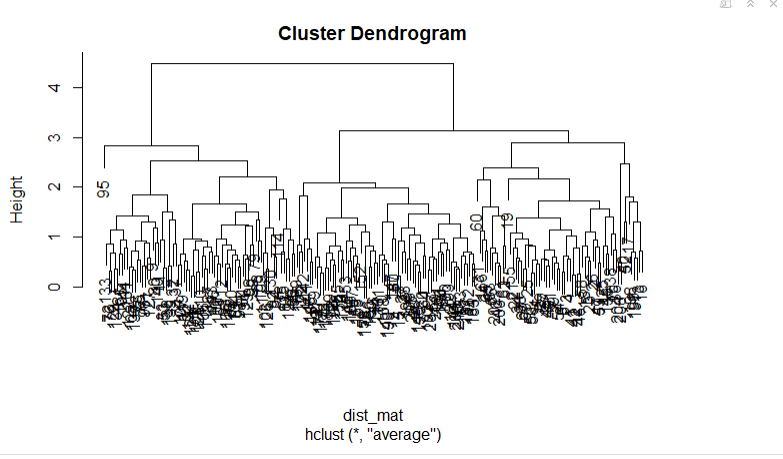

Observe cómo se construye el dendrograma y cómo cada punto de datos se fusiona finalmente en un único conglomerado con la altura (distancia) mostrada en el eje y.

A continuación, puede cortar el dendrograma para crear el número deseado de conglomerados. Como en este caso ya sabe que sólo puede haber tres tipos de trigo, elegirá que el número de conglomerados sea k = 3, o como puede ver en el dendrograma h = 3 obtendrá tres conglomerados. Utilizará la función cutree() de R para cortar el árbol con hclust_avg como un parámetro y el otro parámetro como h = 3 o k = 3.

cut_avg <- cutree(hclust_avg, k = 3)

Si desea ver visualmente los clusters en el dendrograma puede utilizar la función abline() de R para dibujar la línea de corte y superponer compartimentos rectangulares para cada cluster en el árbol con la función rect.hclust() como se muestra en el siguiente código:

plot(hclust_avg)
rect.hclust(hclust_avg , k = 3, border = 2:6)
abline(h = 3, col = 'red')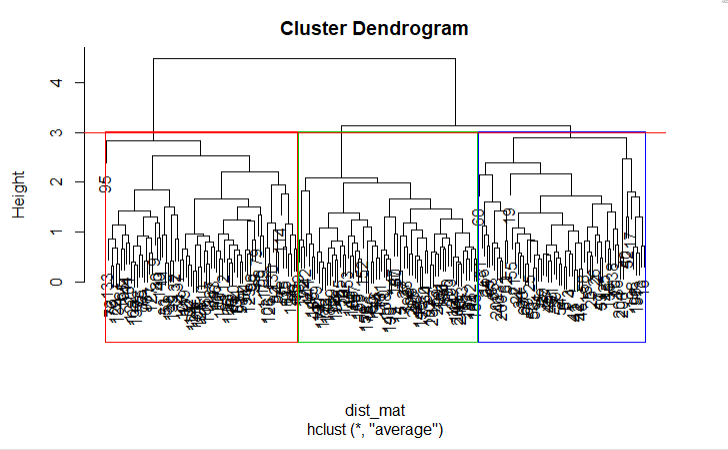

Ahora puedes ver los tres grupos encerrados en tres cajas de colores diferentes. También puede utilizar la función color_branches() de la biblioteca dendextend para visualizar su árbol con ramas de diferentes colores.

Recuerde que puede instalar un paquete en R utilizando el comando install.packages('package_name', dependencies = TRUE).

suppressPackageStartupMessages(library(dendextend))
avg_dend_obj <- as.dendrogram(hclust_avg)
avg_col_dend <- color_branches(avg_dend_obj, h = 3)
plot(avg_col_dend)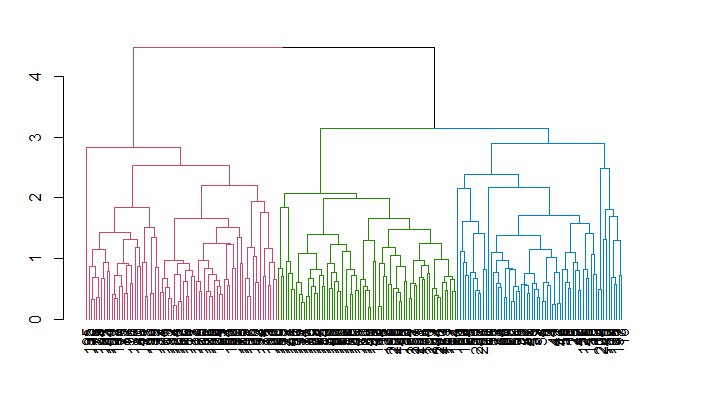

Ahora anexará los resultados de los conglomerados obtenidos de nuevo en el marco de datos original bajo el nombre de columna cluster con mutate(), del paquete dplyr y contará cuántas observaciones se asignaron a cada conglomerado con la función count().

suppressPackageStartupMessages(library(dplyr))
seeds_df_cl <- mutate(seeds_df, cluster = cut_avg)
count(seeds_df_cl,cluster)

Podrá ver cuántas observaciones se asignaron en cada agrupación. Observe que, en realidad, a partir de los datos etiquetados tenía 70 observaciones para cada variedad de trigo.

Es habitual evaluar la tendencia entre dos características basándose en la agrupación que se ha realizado para extraer información más útil de los datos agrupados. Como ejercicio, puede analizar la tendencia entre el trigo perimeter y area cluster-wise con la ayuda del paquete ggplot2.

suppressPackageStartupMessages(library(ggplot2))
ggplot(seeds_df_cl, aes(x=area, y = perimeter, color = factor(cluster))) + geom_point()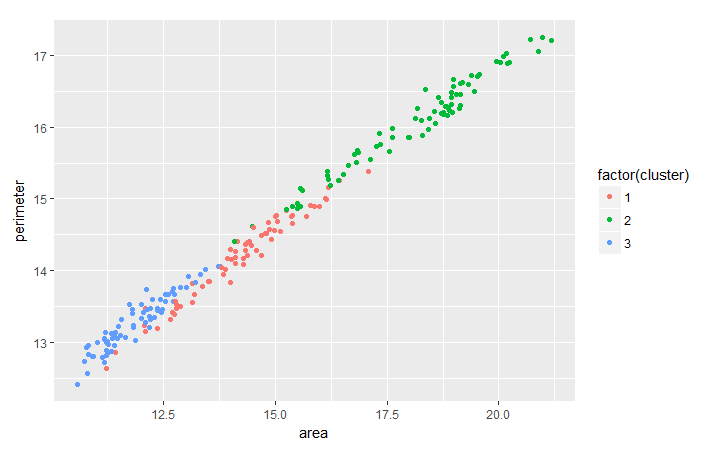

Observa que para todas las variedades de trigo parece existir una relación lineal entre su perímetro y su área.

Dado que ya dispone de las etiquetas verdaderas para este conjunto de datos, también puede considerar la posibilidad de realizar una comprobación cruzada de los resultados de la agrupación utilizando la función table().

table(seeds_df_cl$cluster,seeds_label)

Si echa un vistazo a la tabla que se ha generado, verá claramente tres grupos con 55 elementos o más. En general, puede decirse que sus conglomerados representan adecuadamente los distintos tipos de semillas porque originalmente tenía 70 observaciones para cada variedad de trigo. Los grupos más grandes representan la correspondencia entre las agrupaciones y los tipos reales.

Tenga en cuenta que en muchos casos no dispone realmente de las etiquetas verdaderas. En esos casos, como ya se ha comentado, puede optar por otras medidas como maximizar el índice de Dunn. Puede calcular el índice de dunn utilizando la función dunn() de la biblioteca clValid. Además, se puede considerar la validación cruzada de los resultados creando conjuntos de entrenamiento y de prueba, como se hace en cualquier otro algoritmo de aprendizaje automático, y luego realizar la agrupación cuando se tengan las etiquetas verdaderas.

Comparación con el algoritmo de agrupación K-Means

Es posible que haya oído hablar del algoritmo de agrupación k-means; si no es así, eche un vistazo a este tutorial. Hay muchas diferencias fundamentales entre los dos algoritmos, aunque cualquiera de ellos puede funcionar mejor que el otro en distintos casos. Algunas de las diferencias son:

• Distancia utilizada: La agrupación jerárquica puede manejar prácticamente cualquier métrica de distancia, mientras que k-means se basa en distancias euclidianas.
• Estabilidad de los resultados: k-means requiere un paso aleatorio en su inicialización que puede dar resultados diferentes si se vuelve a ejecutar el proceso. Ese no sería el caso de la agrupación jerárquica.
• Número de grupos: Mientras que en k-means se pueden utilizar gráficos de codo, de silueta, etc. para calcular el número correcto de conglomerados, en jerárquico también se pueden utilizar todos estos métodos, pero con la ventaja añadida de aprovechar el dendrograma.
• Complejidad computacional: K-means es menos costoso computacionalmente que el clustering jerárquico y puede ejecutarse en grandes conjuntos de datos en un tiempo razonable, que es la principal razón por la que k-means es más popular.

Conclusión

¡Enhorabuena! Ha llegado al final de este tutorial. Ha aprendido cómo preprocesar sus datos, los fundamentos de la agrupación jerárquica y los métodos de métrica de distancia y vinculación con los que trabaja, junto con su uso en R. También sabe en qué se diferencia la agrupación jerárquica del algoritmo k-means. ¡Bien hecho! Pero siempre hay mucho más que aprender. Le sugiero que eche un vistazo a nuestro curso Aprendizaje no supervisado en R.