Agrupamento hierárquico em R

Neste tutorial, você aprenderá a executar o agrupamento hierárquico em um conjunto de dados em R. Se quiser aprender sobre agrupamento hierárquico em Python, consulte nosso artigo separado. 

Introdução

Como o próprio nome sugere, os algoritmos de clustering agrupam um conjunto de pontos de dados em subconjuntos ou clusters. O objetivo dos algoritmos é criar clusters que sejam coerentes internamente, mas claramente diferentes uns dos outros externamente. Em outras palavras, as entidades em um cluster devem ser as mais semelhantes possíveis e as entidades em um cluster devem ser as mais diferentes possíveis das entidades em outro.

Em termos gerais, há duas maneiras de agrupar pontos de dados com base na estrutura e na operação algorítmica, a saber, aglomerativa e divisiva.

• Aglomerativo: Uma abordagem aglomerativa começa com cada observação em um cluster distinto (singleton) e mescla sucessivamente os clusters até que um critério de parada seja satisfeito.
• Divisivo: Um método divisivo começa com todos os padrões em um único cluster e realiza a divisão até que um critério de parada seja atendido.

Neste tutorial, você se concentrará na abordagem aglomerativa ou de baixo para cima, na qual você começa com cada ponto de dados como seu próprio cluster e, em seguida, combina os clusters com base em alguma medida de similaridade. A ideia também pode ser facilmente adaptada para métodos de divisão.

A semelhança entre os clusters é geralmente calculada a partir das medidas de dissimilaridade, como a distância euclidiana entre dois clusters. Portanto, quanto maior for a distância entre dois clusters, melhor será.

Há muitas métricas de distância que você pode considerar para calcular a medida de dissimilaridade, e a escolha depende do tipo de dados no conjunto de dados. Por exemplo, se você tiver valores numéricos contínuos no conjunto de dados, poderá usar a distância euclidean. Se os dados forem binários, você poderá considerar a distância Jaccard (útil quando estiver lidando com dados categóricos para agrupamento após ter aplicado a codificação de um ponto). Outras medidas de distância incluem Manhattan, Minkowski, Canberra etc.

Operações de pré-processamento para clustering

Há alguns cuidados que você deve ter antes de começar.

• Dimensionamento

É imperativo que você normalize sua escala de valores de recursos para iniciar o processo de agrupamento. Isso ocorre porque os valores dos recursos de cada observação são representados como coordenadas em um espaço n-dimensional (n é o número de recursos) e, em seguida, as distâncias entre essas coordenadas são calculadas. Se essas coordenadas não forem normalizadas, isso pode levar a resultados falsos.

Por exemplo, suponha que você tenha dados sobre a altura e o peso de três pessoas: A (6ft, 75kg), B (6ft,77kg), C (8ft,75kg). Se você representar esses recursos em um sistema de coordenadas bidimensional, altura e peso, e calcular a distância euclidiana entre eles, a distância entre os pares a seguir seria:

A-B : 2 unidades

A-C : 2 unidades

Bem, a métrica de distância diz que os pares A-B e A-C são semelhantes, mas na realidade eles claramente não são! O par A-B é mais semelhante do que o par A-C. Por isso, é importante dimensionar esses valores primeiro e depois calcular a distância.

Há várias maneiras de normalizar os valores dos recursos. Você pode considerar a padronização de toda a escala de todos os valores dos recursos (x(i)) entre [0,1] (conhecida como normalização mín-máx) aplicando a seguinte transformação:

$ x(s) = x(i) - min(x)/(max(x) - min (x)) $

Você pode usar a função normalize() do R para isso ou você pode escrever sua própria função, como

standardize <- function(x){(x-min(x))/(max(x)-min(x))}

Outro tipo de escalonamento pode ser obtido por meio da seguinte transformação:

$ x(s) = x(i)-mean(x) / sd(x) $

Onde sd(x) é o desvio padrão dos valores dos recursos. Isso garantirá que sua distribuição de valores de recursos tenha uma média de 0 e um desvio padrão de 1. Você pode fazer isso por meio da função scale() no R.

• Imputação de valores ausentes

Também é importante lidar previamente com valores ausentes/nulos/inf em seu conjunto de dados. Há muitas maneiras de lidar com esses valores: uma delas é removê-los ou imputá-los com a média, a mediana, a moda ou usar algumas técnicas avançadas de regressão. O site R tem muitos pacotes e funções para lidar com imputações de valores ausentes, como impute(), Amelia, Mice, Hmisc etc. Você pode ler sobre Amelia neste tutorial.

Algoritmo de agrupamento hierárquico

A principal operação no agrupamento aglomerativo hierárquico é combinar repetidamente os dois clusters mais próximos em um cluster maior. Há três perguntas-chave que precisam ser respondidas primeiro:

• Como você representa um cluster de mais de um ponto?
• Como você determina a "proximidade" dos clusters?
• Quando você para de combinar clusters?

Esperamos que, ao final deste tutorial, você consiga responder a todas essas perguntas. Antes de aplicar o agrupamento hierárquico, vamos dar uma olhada em seu funcionamento:

1. Ele começa calculando a distância entre cada par de pontos de observação e a armazena em uma matriz de distância.
2. Em seguida, ele coloca cada ponto em seu próprio cluster.
3. Em seguida, ele começa a mesclar os pares de pontos mais próximos com base nas distâncias da matriz de distância e, como resultado, a quantidade de clusters diminui em 1.
4. Em seguida, ele recomputa a distância entre o novo cluster e os antigos e os armazena em uma nova matriz de distância.
5. Por fim, ele repete as etapas 2 e 3 até que todos os clusters sejam mesclados em um único cluster.

Há várias maneiras de medir a distância entre os clusters para decidir as regras de agrupamento, e elas são geralmente chamadas de métodos de ligação. Alguns dos métodos comuns de vinculação são:

• Complete-linkage: calcula a distância máxima entre os clusters antes da fusão.

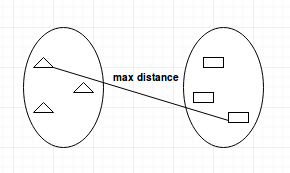
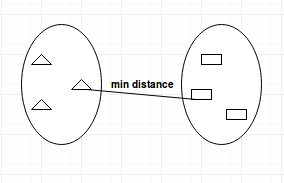
• Single-linkage: calcula a distância mínima entre os clusters antes da fusão. Essa vinculação pode ser usada para detectar valores altos em seu conjunto de dados que podem ser discrepantes, pois eles serão mesclados no final.

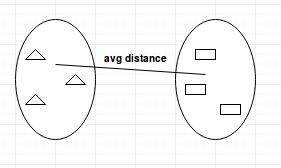
• Average-linkage: calcula a distância média entre os clusters antes da fusão.

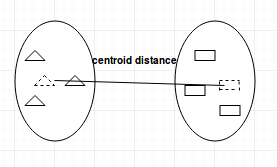
• Centroid-linkage: encontra o centroide do cluster 1 e o centroide do cluster 2 e, em seguida, calcula a distância entre os dois antes da fusão.

A escolha do método de vinculação depende inteiramente de você e não há um método rígido e rápido que sempre lhe proporcione bons resultados. Diferentes métodos de vinculação levam a diferentes clusters.

Dendrogramas

No clustering hierárquico, você categoriza os objetos em uma hierarquia semelhante a um diagrama em forma de árvore, que é chamado de dendrograma. A distância da divisão ou mesclagem (chamada de altura) é mostrada no eixo y do dendrograma abaixo.

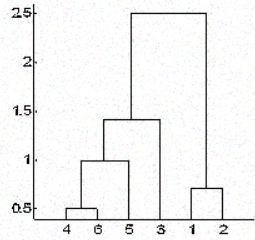
Na figura acima, inicialmente 4 e 6 são combinados em um cluster, chamado de cluster 1, já que eram os mais próximos em distância, seguidos pelos pontos 1 e 2, chamado de cluster 2. Depois disso, o 5 foi mesclado no mesmo cluster 1, seguido pelo 3, resultando em dois clusters. Por fim, os dois clusters são mesclados em um único cluster e é nesse ponto que o processo de clusterização é interrompido.

Uma pergunta que pode tê-lo intrigado até agora é como você decide quando parar de mesclar os clusters? Bem, isso depende do conhecimento de domínio que você tem sobre os dados. Por exemplo, se você estiver agrupando jogadores de futebol em um campo com base em suas posições no campo, que representarão suas coordenadas para o cálculo da distância, você já sabe que deve terminar com apenas dois agrupamentos, pois só pode haver dois times jogando uma partida de futebol.

Mas, às vezes, você também não tem essa informação. Nesses casos, você pode aproveitar os resultados do dendrograma para aproximar o número de clusters. Você corta a árvore do dendrograma com uma linha horizontal em uma altura em que a linha pode percorrer a distância máxima para cima e para baixo sem cruzar o ponto de fusão. No caso acima, seria entre as alturas 1,5 e 2,5, conforme mostrado:

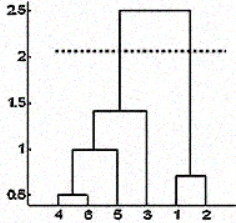
Se você fizer o corte como mostrado, acabará com apenas dois cachos.

Observe que não é necessário fazer um corte apenas nesses locais; você pode escolher qualquer ponto como ponto de corte, dependendo do número de clusters que deseja. Por exemplo, o corte abaixo de 1,5 e acima de 1 lhe dará 3 clusters.

Observe que essa não é uma regra rígida e rápida para decidir o número de clusters. Você também pode considerar gráficos como o gráfico de silhueta, o gráfico de cotovelo ou algumas medidas numéricas, como o índice de Dunn, a gama de Hubert etc., que mostram a variação do erro com o número de clusters (k), e você escolhe o valor de k em que o erro é menor.

Medindo a qualidade dos clusters

Talvez a parte mais importante de qualquer tarefa de aprendizado não supervisionado seja a análise dos resultados. Depois de realizar o agrupamento usando qualquer algoritmo e qualquer conjunto de parâmetros, você precisa se certificar de que o fez corretamente. Mas como você determina isso?

Bem, há muitas medidas para fazer isso, talvez a mais popular seja o Dunn's Index. O índice de Dunn é a razão entre as distâncias mínimas entre clusters e o diâmetro máximo intra-cluster. O diâmetro de um cluster é a distância entre seus dois pontos mais distantes. Para obter clusters bem separados e compactos, você deve buscar um índice de Dunn mais alto.

Clusterização hierárquica em ação

Agora você aplicará o conhecimento que adquiriu para resolver um problema do mundo real.

Você aplicará o clustering hierárquico no conjunto de dados seeds. Esse conjunto de dados consiste em medições de propriedades geométricas de grãos pertencentes a três variedades diferentes de trigo: Kama, Rosa e Canadense. Ele tem variáveis que descrevem as propriedades das sementes, como área, perímetro, coeficiente de assimetria etc. Há 70 observações para cada variedade de trigo. Você pode encontrar os detalhes sobre o conjunto de dados aqui.

Comece importando o conjunto de dados em um dataframe com a função read.csv().

Observe que o arquivo não tem nenhum cabeçalho e é separado por tabulação. Para manter a reprodutibilidade dos resultados, você precisa usar a função set.seed().

set.seed(786)
file_loc <- 'seeds.txt'
seeds_df <- read.csv(file_loc,sep = '\t',header = FALSE)

Como o conjunto de dados não tem nenhum nome de coluna, você mesmo dará o nome às colunas a partir da descrição dos dados.

feature_name <- c('area','perimeter','compactness','length.of.kernel','width.of.kernal','asymmetry.coefficient','length.of.kernel.groove','type.of.seed')
colnames(seeds_df) <- feature_name

É aconselhável reunir algumas informações básicas úteis sobre o conjunto de dados, como suas dimensões, tipos e distribuição de dados, número de NAs etc. Você fará isso usando as funções str(), summary() e is.na() no R.

str(seeds_df)
summary(seeds_df)
any(is.na(seeds_df))

Observe que esse conjunto de dados tem todas as colunas como valores numéricos. Não há valores ausentes nesse conjunto de dados que você precise limpar antes do clustering. Mas as escalas dos recursos são diferentes e você precisa normalizá-las. Além disso, os dados estão rotulados e você já tem as informações sobre qual observação pertence a qual variedade de trigo.

Agora, você armazenará os rótulos em uma variável separada e excluirá a coluna type.of.seed do seu conjunto de dados para fazer o clustering. Posteriormente, você usará os rótulos verdadeiros para verificar a qualidade do seu agrupamento.

seeds_label <- seeds_df$type.of.seed
seeds_df$type.of.seed <- NULL
str(seeds_df)

Como você pode notar, a coluna true label foi removida do conjunto de dados.

Agora você usará a função scale() do site R para dimensionar todos os valores da coluna.

seeds_df_sc <- as.data.frame(scale(seeds_df))
summary(seeds_df_sc)

Observe que a média de todas as colunas é 0 e o desvio padrão é 1. Agora que você pré-processou seus dados, é hora de criar a matriz de distância. Como todos os valores aqui são valores numéricos contínuos, você usará o método de distância euclidean.

dist_mat <- dist(seeds_df_sc, method = 'euclidean')

Nesse ponto, você deve decidir qual método de ligação deseja usar e prosseguir com o clustering hierárquico. Você pode experimentar todos os tipos de métodos de vinculação e depois decidir qual deles teve melhor desempenho. Aqui você prosseguirá com o método de vinculação average.

Você criará seu dendrograma plotando o objeto de cluster hierárquico que será criado com hclust(). Você pode especificar o método de vinculação por meio do argumento method.

hclust_avg <- hclust(dist_mat, method = 'average')
plot(hclust_avg)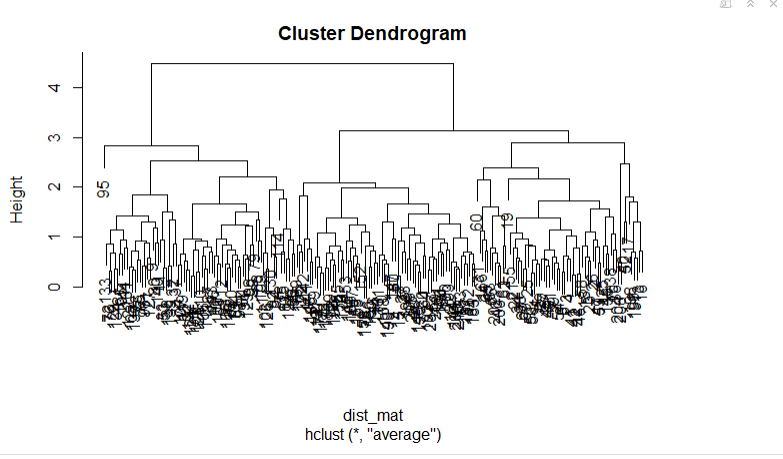

Observe como o dendrograma é construído e cada ponto de dados finalmente se funde em um único cluster com a altura (distância) mostrada no eixo y.

Em seguida, você pode cortar o dendrograma para criar o número desejado de clusters. Como nesse caso você já sabe que pode haver apenas três tipos de trigo, você escolherá o número de clusters como k = 3 ou, como você pode ver no dendrograma h = 3, obterá três clusters. Você usará a função cutree() do R para cortar a árvore com hclust_avg como um parâmetro e o outro parâmetro como h = 3 ou k = 3.

cut_avg <- cutree(hclust_avg, k = 3)

Se você quiser ver visualmente os clusters no dendrograma, poderá usar a função abline() do R para desenhar a linha de corte e sobrepor compartimentos retangulares para cada cluster na árvore com a função rect.hclust(), conforme mostrado no código a seguir:

plot(hclust_avg)
rect.hclust(hclust_avg , k = 3, border = 2:6)
abline(h = 3, col = 'red')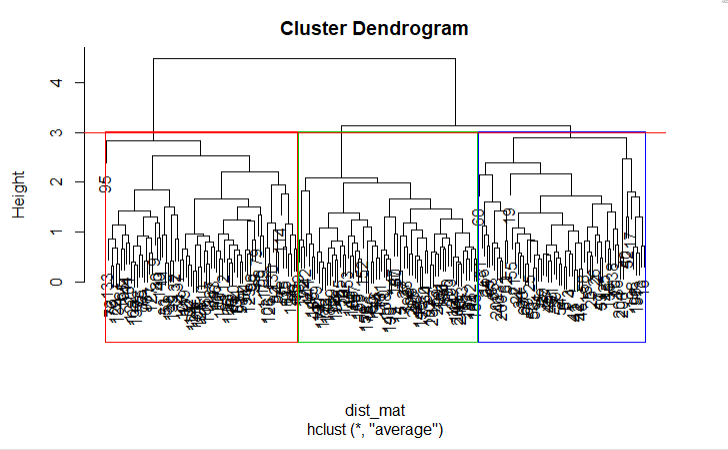

Agora você pode ver os três clusters dentro de três caixas coloridas diferentes. Você também pode usar a função color_branches() da biblioteca dendextend para visualizar sua árvore com ramos de cores diferentes.

Lembre-se de que você pode instalar um pacote no R usando o comando install.packages('package_name', dependencies = TRUE).

suppressPackageStartupMessages(library(dendextend))
avg_dend_obj <- as.dendrogram(hclust_avg)
avg_col_dend <- color_branches(avg_dend_obj, h = 3)
plot(avg_col_dend)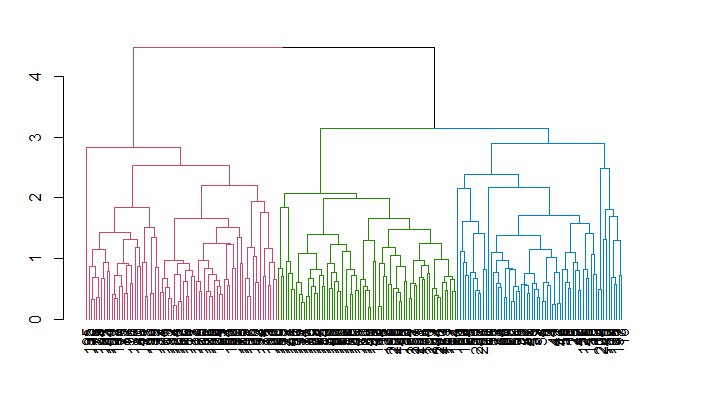

Agora, você anexará os resultados do cluster obtidos de volta ao dataframe original sob o nome da coluna cluster com mutate(), do pacote dplyr e contará quantas observações foram atribuídas a cada cluster com a função count().

suppressPackageStartupMessages(library(dplyr))
seeds_df_cl <- mutate(seeds_df, cluster = cut_avg)
count(seeds_df_cl,cluster)

Você poderá ver quantas observações foram atribuídas em cada cluster. Observe que, na realidade, com base nos dados rotulados, você tinha 70 observações para cada variedade de trigo.

É comum avaliar a tendência entre dois recursos com base no agrupamento que você fez para extrair insights mais úteis dos dados em termos de agrupamento. Como exercício, você pode analisar a tendência entre perimeter e area do trigo em termos de cluster com a ajuda do pacote ggplot2.

suppressPackageStartupMessages(library(ggplot2))
ggplot(seeds_df_cl, aes(x=area, y = perimeter, color = factor(cluster))) + geom_point()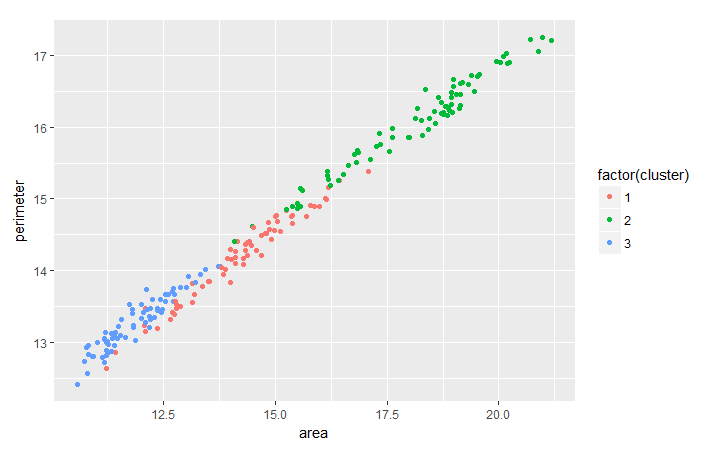

Observe que, para todas as variedades de trigo, parece haver uma relação linear entre o perímetro e a área.

Como você já tem os rótulos verdadeiros para esse conjunto de dados, também pode considerar a verificação cruzada dos resultados do clustering usando a função table().

table(seeds_df_cl$cluster,seeds_label)

Se você der uma olhada na tabela gerada, verá claramente três grupos com 55 elementos ou mais. De modo geral, pode-se dizer que seus clusters representam adequadamente os diferentes tipos de sementes porque originalmente você tinha 70 observações para cada variedade de trigo. Os grupos maiores representam a correspondência entre os clusters e os tipos reais.

Observe que, em muitos casos, você não tem os rótulos verdadeiros. Nesses casos, como já discutido, você pode optar por outras medidas, como a maximização do índice de Dunn. Você pode calcular o índice de Dunn usando a função dunn() da biblioteca clValid. Além disso, você pode considerar fazer a validação cruzada dos resultados criando conjuntos de treinamento e teste, como em qualquer outro algoritmo de aprendizado de máquina, e depois fazer o agrupamento quando tiver os rótulos verdadeiros.

Comparação com o algoritmo de agrupamento K-Means

Talvez você já tenha ouvido falar do algoritmo de agrupamento k-means; caso contrário, dê uma olhada neste tutorial. Há muitas diferenças fundamentais entre os dois algoritmos, embora qualquer um deles possa ter um desempenho melhor do que o outro em diferentes casos. Algumas das diferenças são:

• Distância utilizada: O agrupamento hierárquico pode lidar virtualmente com qualquer métrica de distância, enquanto o k-means depende de distâncias euclidianas.
• Estabilidade dos resultados: o k-means requer uma etapa aleatória em sua inicialização que pode produzir resultados diferentes se o processo for executado novamente. Esse não seria o caso no clustering hierárquico.
• Número de clusters: Embora você possa usar gráficos de cotovelo, gráficos de silhueta etc. para calcular o número correto de clusters no k-means, o hierárquico também pode usar todos esses recursos, mas com o benefício adicional de aproveitar o dendrograma para isso.
• Complexidade de computação: O K-means é menos dispendioso do ponto de vista computacional do que o clustering hierárquico e pode ser executado em grandes conjuntos de dados em um período de tempo razoável, o que é o principal motivo pelo qual o K-means é mais popular.

Conclusão

Parabéns! Você chegou ao final deste tutorial. Você aprendeu como pré-processar seus dados, os conceitos básicos de clustering hierárquico e os métodos de métricas de distância e vinculação com os quais ele trabalha, além de seu uso no R. Você também sabe como o clustering hierárquico difere do algoritmo k-means. Muito bem! Mas sempre há muito mais a aprender. Sugiro que você dê uma olhada em nosso curso Aprendizado não supervisionado em R.