Régression linéaire dans Excel : Un guide complet pour les débutants

Qu'est-ce que la régression linéaire ?

La régression linéaire est l'une des techniques d'apprentissage automatique les plus simples. Il s'agit de prédire la valeur d'une variable dépendante en fonction d'une ou plusieurs variables indépendantes.

Par exemple, la régression linéaire peut être appliquée pour prédire les prix des maisons en fonction de leur taille ou pour prédire le poids d'une personne en fonction de sa taille. Les modèles de régression linéaire sont principalement classés en deux catégories : la régression linéaire simple et la régression linéaire multiple.

• La régression linéaire simple se concentre sur la modélisation de la relation entre une variable dépendante et une variable indépendante.
• La régression linéaire multiple fait intervenir plusieurs variables indépendantes pour prédire la variable dépendante.

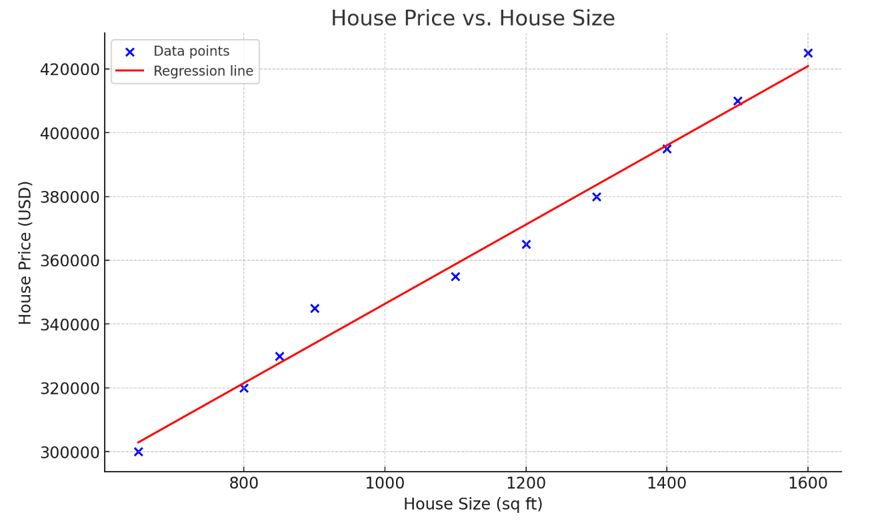
Image par OpenAI

Le graphique ci-dessus représente une régression linéaire simple, modélisant la relation entre la taille du logement (variable indépendante) et le prix du logement (variable dépendante). Comme le montre la visualisation, plus la maison est grande, plus elle est chère.

L'équation de la droite de régression est la suivante :

y = mx + c + ⍷

Si la formule ci-dessus vous semble familière, c'est que vous avez probablement appris à l'école que y = mx + c est l'équation d'une droite. Dans cette équation :

• Y est la variable dépendante
• X est la variable indépendante
• M est la pente, qui quantifie la variation de la variable dépendante pour une variation d'une unité de la variable indépendante.
• C est l'ordonnée à l'origine, qui représente la valeur de y lorsque x est égal à 0.

⍷ représente le résidu ou le terme d'erreur. Il s'agit de la différence entre la valeur réelle et la valeur prédite par la valeur de régression. distingue une droite de régression d'une droite purement déterministe, ce qui fait que la relation entre x et y n'est pas parfaitement prévisible.

Pour un guide plus complet sur le sujet, lisez notre article expliquant l'essentiel de la régression linéaire.

Pourquoi Excel pour la régression linéaire ?

Voici quelques facteurs qui font d'Excel un outil efficace pour effectuer une régression linéaire :

1. Plate-forme unifiée

En 2024, Excel est utilisé par plus de 731 000 entreprises aux États-Unis et par un nombre incalculable d'autres dans le monde, selon Statista. Les cadres, à tous les niveaux de l'organisation, utilisent Excel pour la gestion des données et l'établissement de rapports.

En créant des modèles prédictifs tels que la régression linéaire dans Excel, les entreprises peuvent consolider leurs activités de reporting et de modélisation prédictive au sein d'une plateforme unique. Cela permet aux organisations de rationaliser les flux de travail au lieu d'avoir à passer constamment d'un environnement de programmation à une feuille de calcul Excel.

2. Facilité d'utilisation

Si vous êtes un débutant dans le secteur des données, la simple idée de construire un modèle prédictif peut vous sembler intimidante en raison du codage qu'elle implique. Excel simplifie ce processus en vous permettant de travailler dans une interface qui vous est déjà familière. Avec Excel, la construction d'un modèle de régression linéaire devient un processus simple, réalisable en quelques clics.

3. Rapports et visualisation

Excel offre de solides capacités de visualisation, vous permettant de représenter graphiquement la relation entre différentes variables afin de mieux les comprendre. En outre, il simplifie la création de rapports, garantissant que les visualisations peuvent être facilement intégrées dans des présentations PowerPoint pour une communication efficace avec les parties prenantes.

Comment mettre en œuvre la régression linéaire dans Excel

Avant de vous plonger dans ce tutoriel, téléchargez le jeu de données disponible sur ce dépôt GitHub. Cet ensemble de données a été spécifiquement créé par OpenAI à des fins éducatives. La maîtrise des opérations de base d'une feuille de calcul, telles que la saisie de données, l'application de formules simples et la navigation dans les feuilles de calcul, vous permettra de mieux suivre ce didacticiel.

Étape 1 : Data Analysis ToolPak dans Excel

Tout d'abord, nous devons activer le Data Analysis ToolPak dans Excel. Il s'agit d'un programme complémentaire d'Excel qui fournit une variété d'outils d'analyse de données, y compris celui que nous utiliserons pour la régression linéaire.

Pour ce faire, ouvrez d'abord le fichier Excel et allez dans Fichier -> Options. Dans la boîte de dialogue Options, sélectionnez Compléments -> Compléments Excel et cliquez sur Aller :

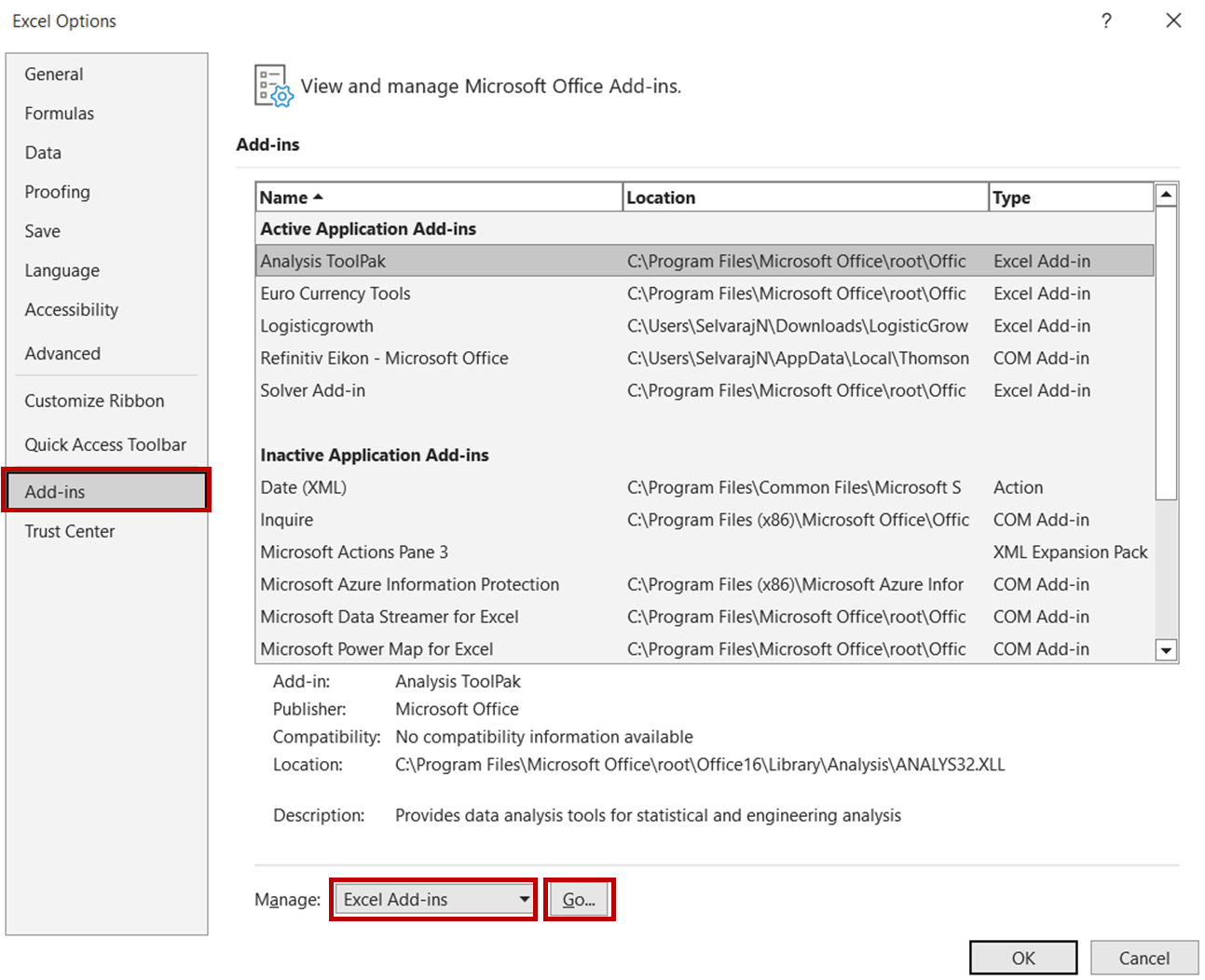
Dans la boîte de dialogue Compléments, cochez l'option Analysis ToolPak et cliquez sur OK.

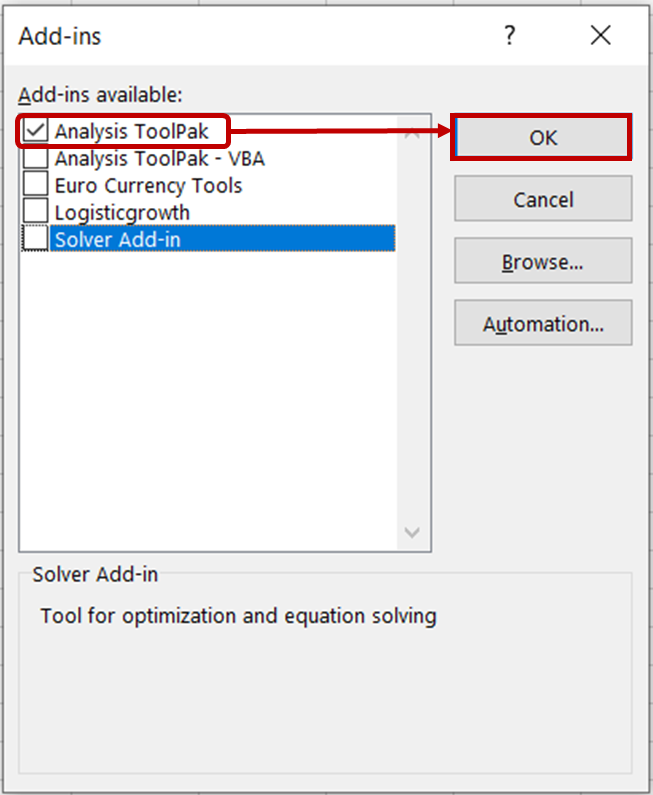
Vous devriez maintenant voir les outils d'analyse de données dans l'onglet Données.

Étape 2 : Effectuer une régression linéaire dans Excel

Maintenant que nous avons activé le Data Analysis ToolPak, nous pouvons procéder à une régression linéaire sur l'ensemble des données. Ouvrez l'ensemble de données sur les ventes de glaces et accédez à l'onglet Données. Dans le groupe Analyse, cliquez sur Analyse des données.

Sélectionnez ensuite Régression dans la liste des outils d'analyse et cliquez sur OK.

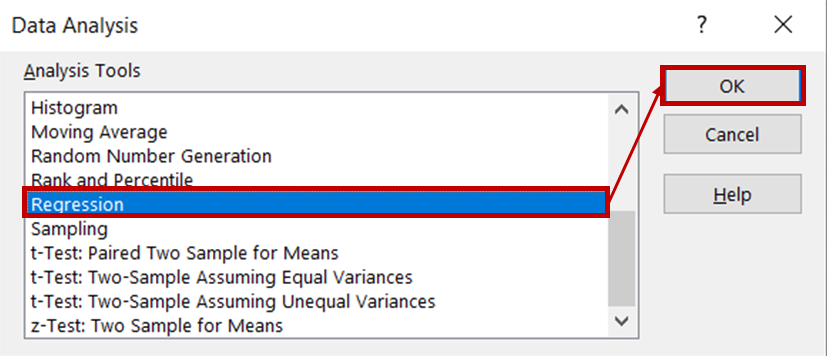
Dans la boîte de dialogue de régression, pour la Plage d'entrée Y, sélectionnez la colonne contenant les données sur les ventes de glaces. Pour la plage Input X, sélectionnez les colonnes contenant les données de température et de prix. Veillez à ce que la case Étiquettes soit cochée, car cela aidera Excel à reconnaître les en-têtes et à traiter les lignes restantes comme des données numériques. Dans la section Options de sortie , sélectionnez Nouvelle feuille de calcul pour afficher les résultats dans une nouvelle feuille de calcul.

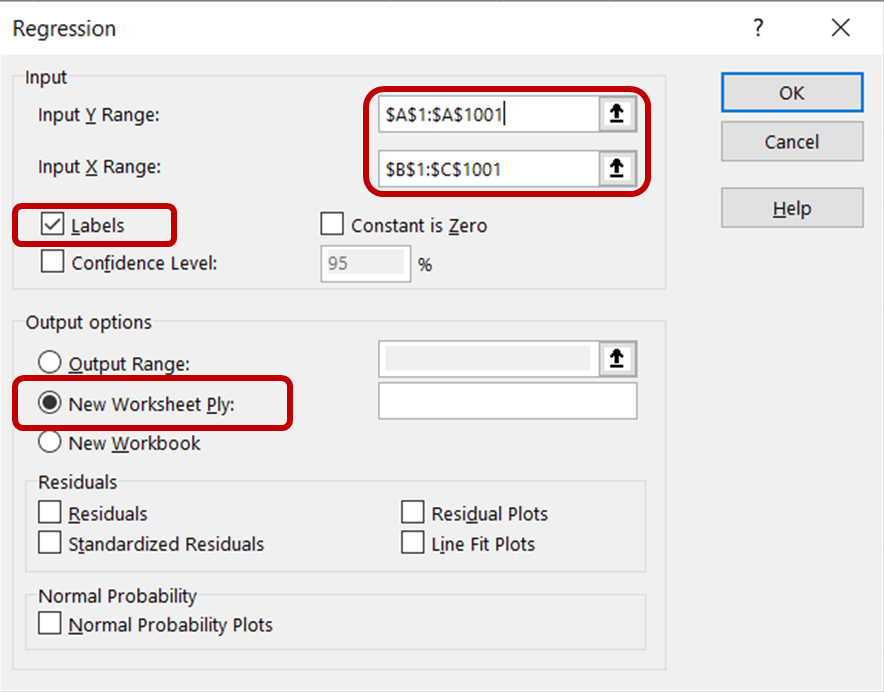
Cliquez ensuite sur OK pour exécuter l'analyse de régression sur l'ensemble de données.

Étape 3 : Interprétation des résultats

Après avoir effectué la régression, vous devriez voir une nouvelle feuille de calcul apparaître automatiquement dans le fichier Excel, présentant un ensemble de tableaux de résultats qui ressemblent à ceci :

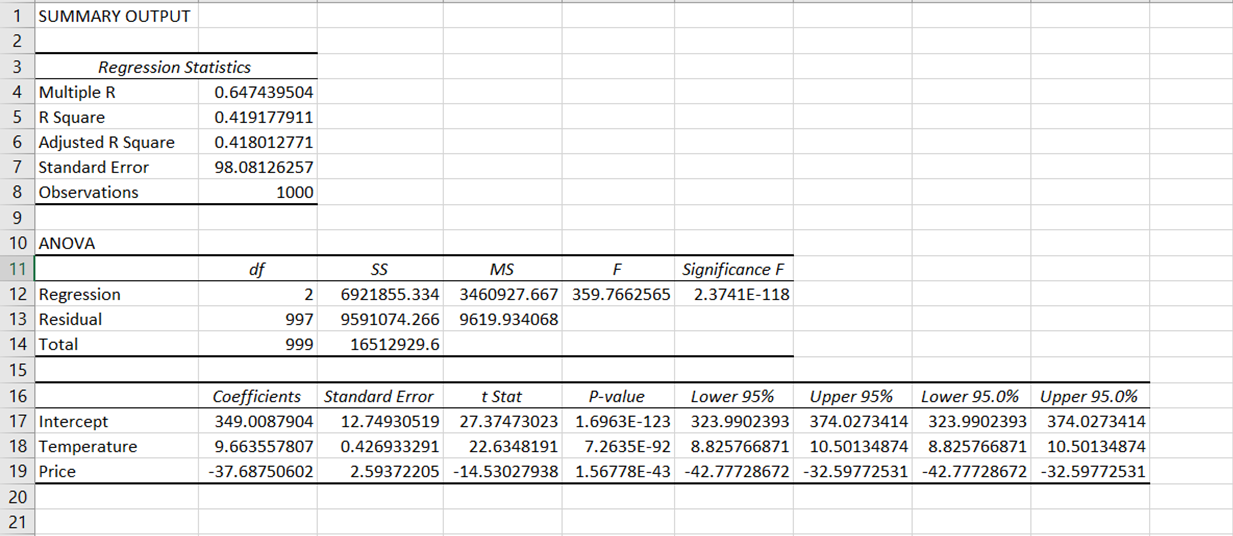
Les résultats de la régression ont été décomposés en plusieurs éléments : statistiques de régression, ANOVA, coefficients, erreur standard, t Stat, valeur P et intervalle de confiance.

Examinons chacun de ces éléments plus en détail :

1. Statistiques sommaires

Excel présente les statistiques récapitulatives suivantes à la suite de l'analyse de régression :

Multiple R

Il s'agit d'un coefficient de corrélation qui mesure la force et la direction d'une relation linéaire entre des variables. Il varie de -1 à 1, les valeurs proches de -1 ou de 1 indiquant une forte relation et les valeurs proches de 0 suggérant une absence de corrélation.

Dans notre analyse, le coefficient de corrélation est d'environ 0,65, ce qui montre une corrélation positive modérée entre notre variable dépendante (ventes de glaces) et les variables indépendantes (prix et température).

Carré R

^R2 est une mesure statistique qui nous indique dans quelle mesure les données correspondent au modèle de régression. Il s'agit du carré du coefficient de corrélation, R multiple, qui représente la proportion de la variance de la variable dépendante qui peut être expliquée par les variables indépendantes.

^R2 est compris entre 0 et 1, les valeurs les plus proches de 1 suggérant une meilleure adéquation du modèle. Notre^R2 est d'environ 0,419, ce qui signifie qu'environ 41,9 % de la variance des ventes de glaces peut être expliquée par le modèle.

R carré ajusté

Il s'agit de la valeur R au carré ajustée en fonction du nombre de prédicteurs dans le modèle. Il s'agit généralement d'une meilleure mesure lorsque l'on compare des modèles comportant différents nombres de prédicteurs. Dans notre cas, le^R2 ajusté est de 0,418. Ce chiffre est très proche de notre^R2, ce qui suggère que les variables indépendantes que nous avons incluses (température et prix) sont pertinentes pour le modèle et n'ont pas introduit de pénalité importante.

Erreur standard

L'erreur standard mesure la distance moyenne entre les valeurs observées et la droite de régression. Une erreur standard plus petite est préférable car elle signifie que la droite de régression correspond mieux aux données.

Dans notre cas, l'erreur standard est d'environ 98,05, ce qui indique que les valeurs réelles des ventes de glace s'écartent des valeurs prédites d'environ 98,05 unités.

Observations

Il s'agit du nombre total de points de données (lignes) analysés dans l'ensemble de données, à l'exclusion de tout en-tête.

2. ANOVA (analyse de la variance)

ANOVA signifie analyse de la variance. Il s'agit d'une technique statistique qui fournit des informations sur le niveau de variabilité au sein d'un modèle de régression :

Degrés de liberté (df)

Cela représente le nombre de valeurs dans le calcul final qui sont libres de varier. Dans le contexte de l'ANOVA, la "régression" df fait référence au nombre de variables indépendantes dans le modèle, qui est de 2. Le df "résiduel" est calculé en soustrayant le nombre de variables indépendantes et 1 du nombre total d'observations. Dans notre cas, il s'agit de 997.

Somme des carrés (SS)

Cela permet de quantifier la variation. La "SS de régression" mesure la variation de la variable dépendante qui peut être expliquée par le modèle. La "SS résiduelle" représente la variation inexpliquée.

Moyenne quadratique (MS)

Elle est obtenue en divisant la somme des carrés (SS) par les degrés de liberté (df).

Statistique F (F)

Cette statistique détermine la signification globale du modèle. Une valeur F plus élevée indique que le modèle correspond mieux aux données.

Signification F

Il s'agit de la valeur P associée à la statistique F. Une valeur p très faible (inférieure à 0,05) indique que votre modèle correspond mieux aux données qu'un modèle sans variables indépendantes. Dans notre cas, la valeur F de signification est inférieure à 0,05, ce qui indique que le modèle s'adapte bien aux données.

3. Coefficients

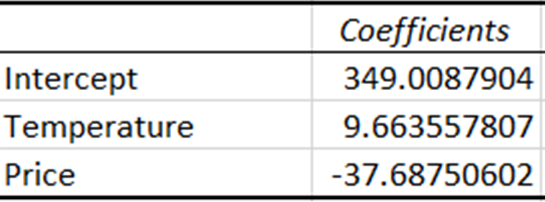
Les coefficients représentent la variation estimée de la variable dépendante pour une variation d'une unité de la variable indépendante.

Le coefficient de température indique que pour chaque augmentation d'une unité de la température, les ventes augmentent d'environ 9,66 unités. Inversement, le coefficient du prix indique que les ventes diminuent d'environ 37,69 unités pour une augmentation d'une unité du prix.

4. Erreur standard

L'erreur standard mesure la distance moyenne entre les valeurs observées et la droite de régression. Une erreur standard plus faible indique un meilleur modèle.

5. t Stat

La statistique t est le coefficient divisé par son erreur standard. Une statistique t plus importante indique que le coefficient est différent de zéro, ce qui signifie qu'il a un impact plus important sur la variable dépendante.

6. Valeur P

Les valeurs P indiquent la probabilité d'observer une statistique t aussi extrême que celle observée en supposant que l'hypothèse nulle est vraie (c'est-à-dire que le coefficient d'une variable indépendante est égal à 0).

En termes simples, plus la statistique t est grande et plus la valeur P est petite, plus l'hypothèse nulle est réfutée, ce qui permet de conclure que les variables indépendantes (prix et température) ont un impact statistiquement significatif sur la variable dépendante (ventes de glaces).

7. Intervalles de confiance (95 % inférieurs et 95 % supérieurs)

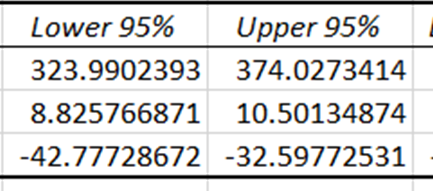
Les intervalles de confiance indiquent les limites inférieures et supérieures dans lesquelles les coefficients réels des variables indépendantes sont censés se situer, avec un niveau de confiance de 95 %. Étant donné que les intervalles de confiance pour le prix et la température sont différents de zéro, ces coefficients ont un impact statistiquement significatif sur la prévision des ventes de glaces.

Comment visualiser une régression linéaire dans Excel ?

La visualisation de la relation entre deux variables peut grandement améliorer votre compréhension de l'ensemble des données. Alors que la boîte à outils d'analyse d'Excel fournit des statistiques sommaires détaillées, une représentation graphique peut instantanément vous montrer la force et la direction d'une relation entre des variables.

La création d'un diagramme de dispersion avec une ligne de tendance est un moyen efficace de visualiser cette relation et peut être réalisée en moins de cinq minutes. Cette technique de visualisation vous permet de voir d'un coup d'œil l'impact d'une variable sur une autre.

Voici comment visualiser la relation entre les "ventes de glaces" et la "température" :

1. Insérer un nuage de points

Tout d'abord, mettez en surbrillance les cellules contenant les variables "Ventes de glaces" et "Température". Accédez ensuite à l'onglet "Insertion" et cliquez sur l'icône "Diagramme de dispersion" :

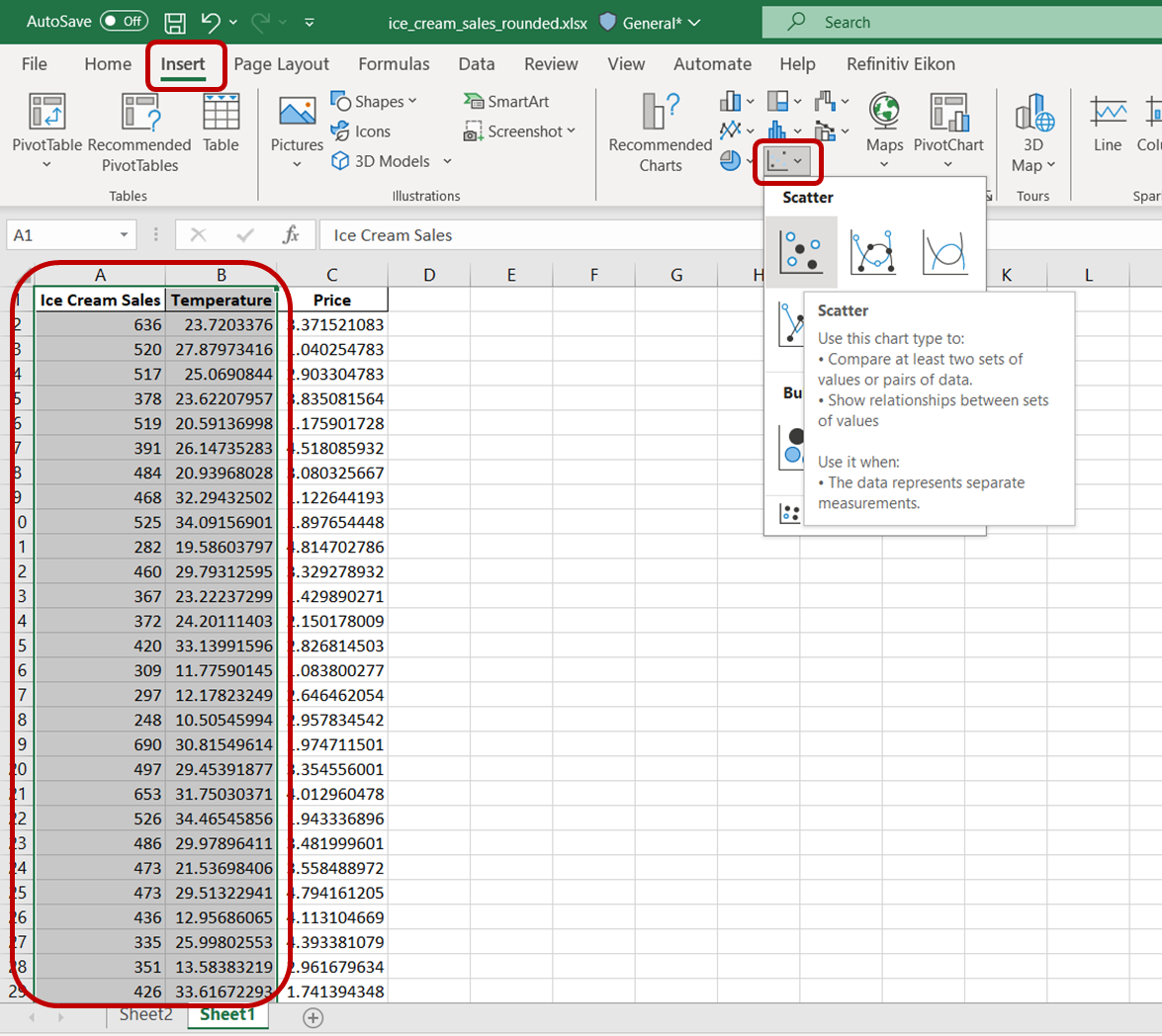
Vous obtiendrez un diagramme de dispersion simple qui ressemble à ceci :

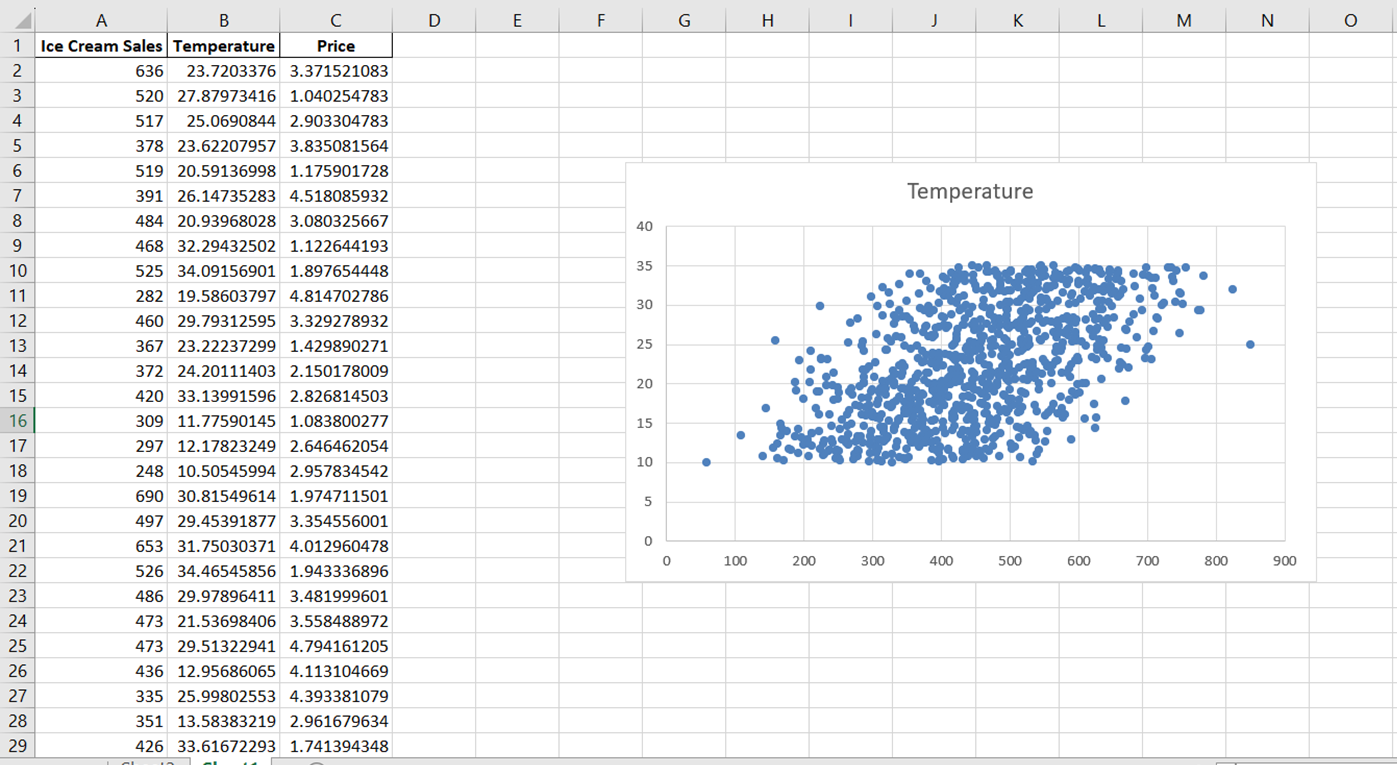
2. Réétiqueter le graphique et les axes

Renommons maintenant le graphique pour décrire précisément la relation que nous visualisons. Il suffit de cliquer sur le titre du graphique et de le remplacer par "Relation entre les ventes de glaces et la température".

Ensuite, pour modifier l'étiquette de l'axe des x, accédez à "Chart Design". Dans le menu déroulant "Add Chart Element", sélectionnez "Axis Titles" -> "Primary Horizontal" :

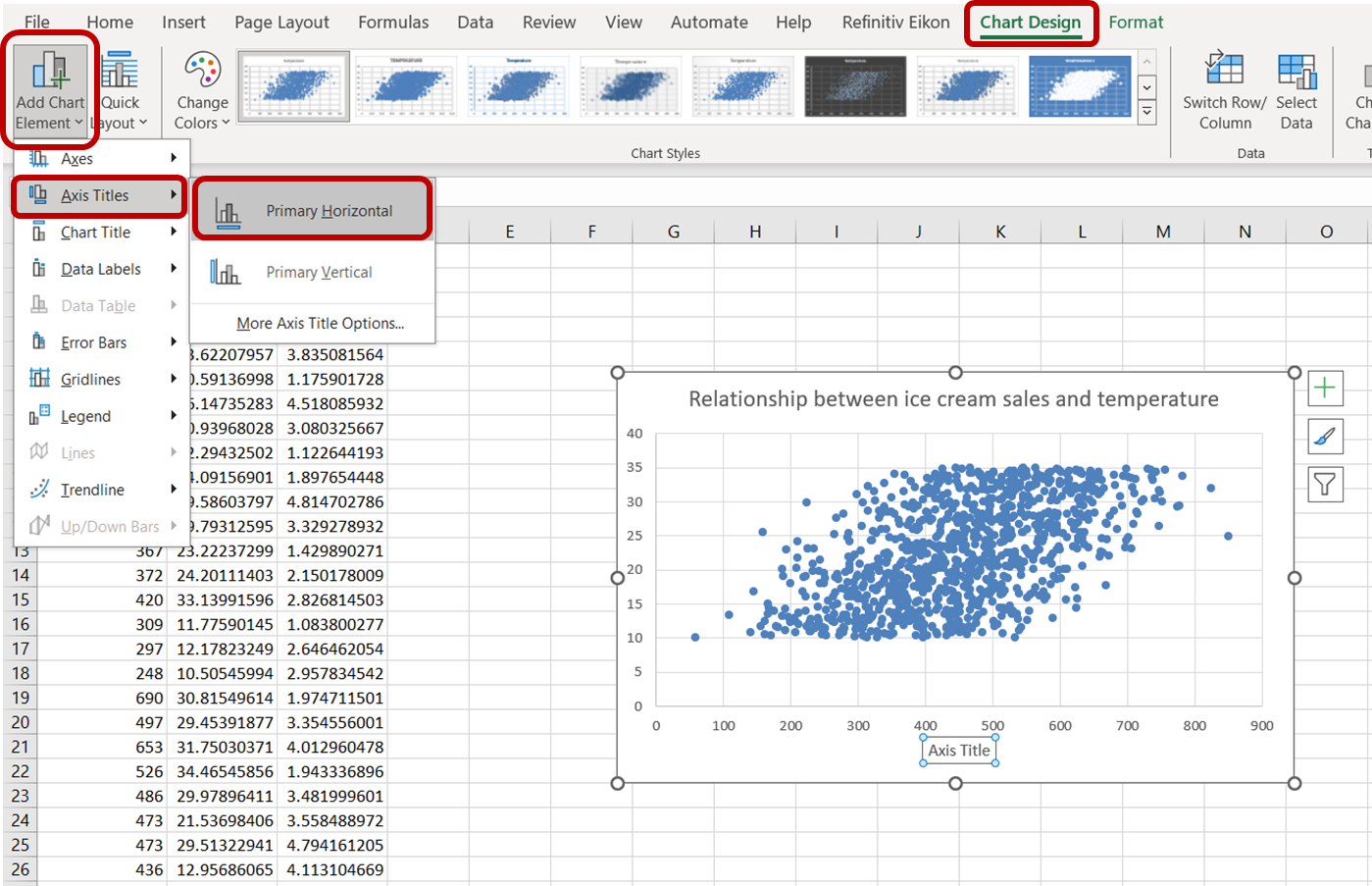
Cliquez sur le titre de l'axe par défaut qui apparaît et tapez "Ventes de glaces" pour étiqueter l'axe avec précision. Faites de même pour l'axe des ordonnées en sélectionnant "Vertical primaire" et en remplaçant le titre de l'axe par "Température :"

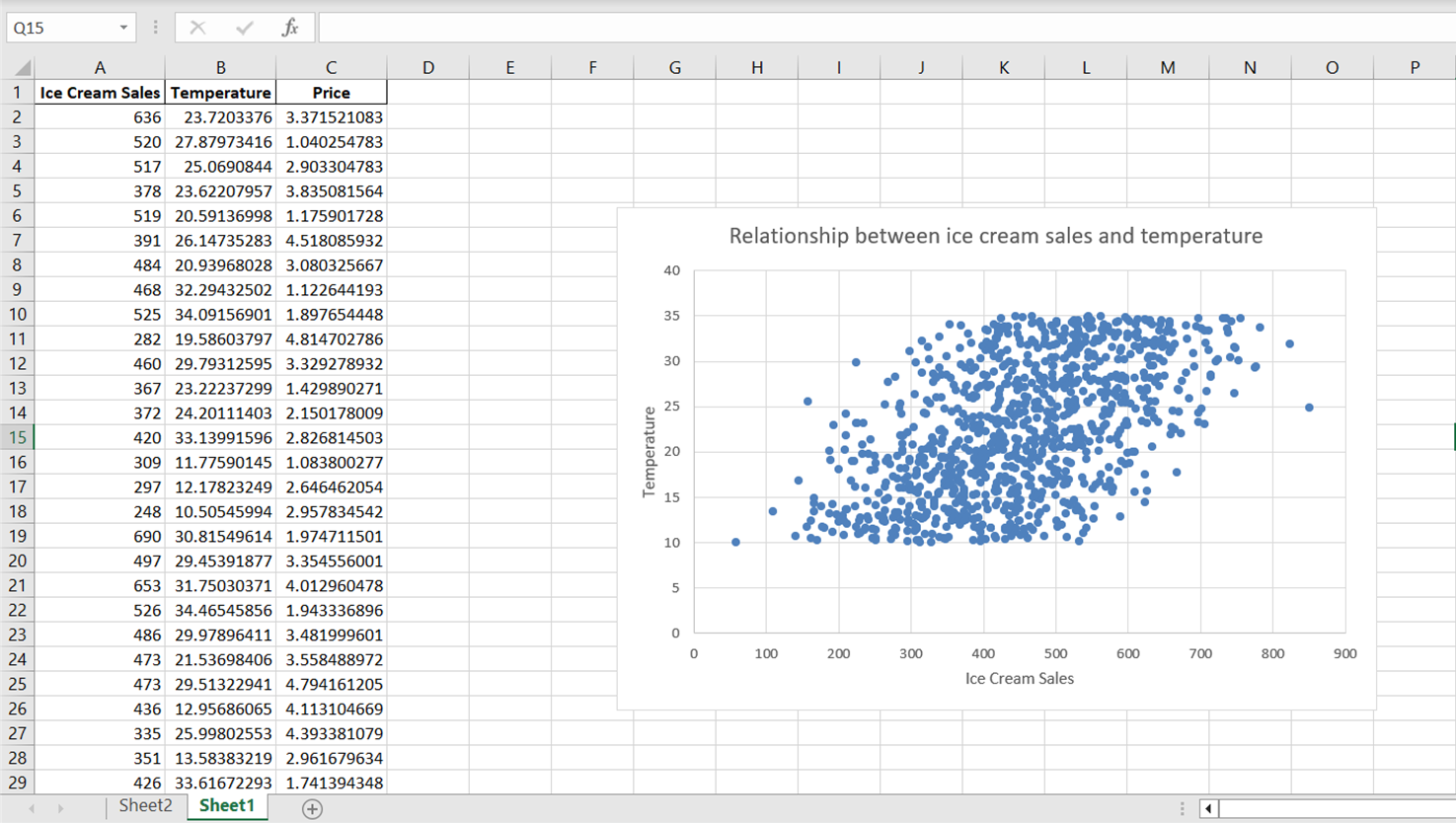
3. Ajouter une ligne de tendance

Remarquez que si le diagramme de dispersion révèle une direction générale dans la relation entre la température et les ventes de glaces, les points de données semblent être largement dispersés. Pour mieux résumer cette relation, y compris sa direction générale et sa pente, incorporons une ligne de tendance ou une ligne de meilleur ajustement.

Pour ajouter une ligne de tendance à ce graphique, il suffit de cliquer sur n'importe quel point de données de ce nuage de points. Cette action permet de sélectionner tous les points de données du graphique. Cliquez ensuite avec le bouton droit de la souris sur les points de données sélectionnés. Dans le menu qui apparaît, choisissez "Ajouter une ligne de tendance".

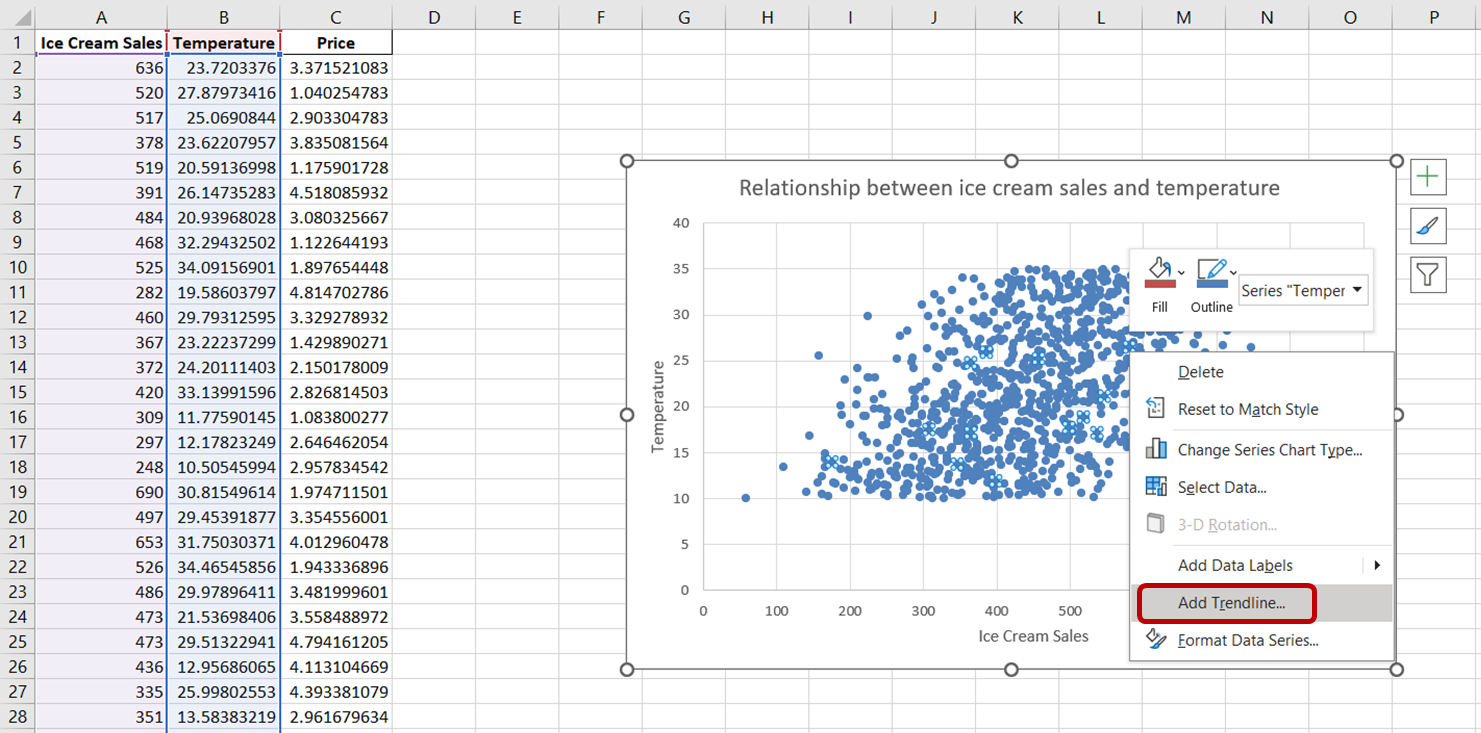
Vous devriez voir apparaître une ligne pointillée sur le graphique, illustrant la direction générale de la relation entre les variables :

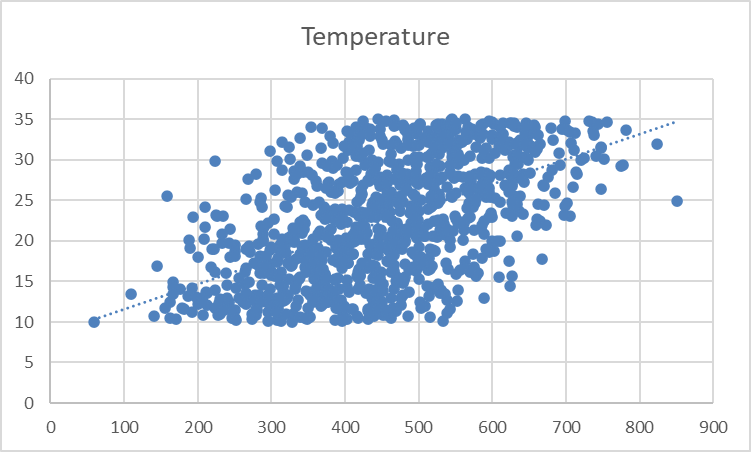
4. Format de la ligne de tendance

La ligne de tendance semble faible et subtile. Ajustons sa mise en forme pour une meilleure visibilité.

Tout d'abord, cliquez sur la ligne de tendance pour la sélectionner. Le volet de tâches "Format Trendline" apparaît à droite de votre fenêtre Excel. Dans ce volet, sélectionnez l'option "Remplir et tracer". Ensuite, augmentez la largeur de la ligne de tendance à 3 points et changez sa couleur en rouge :

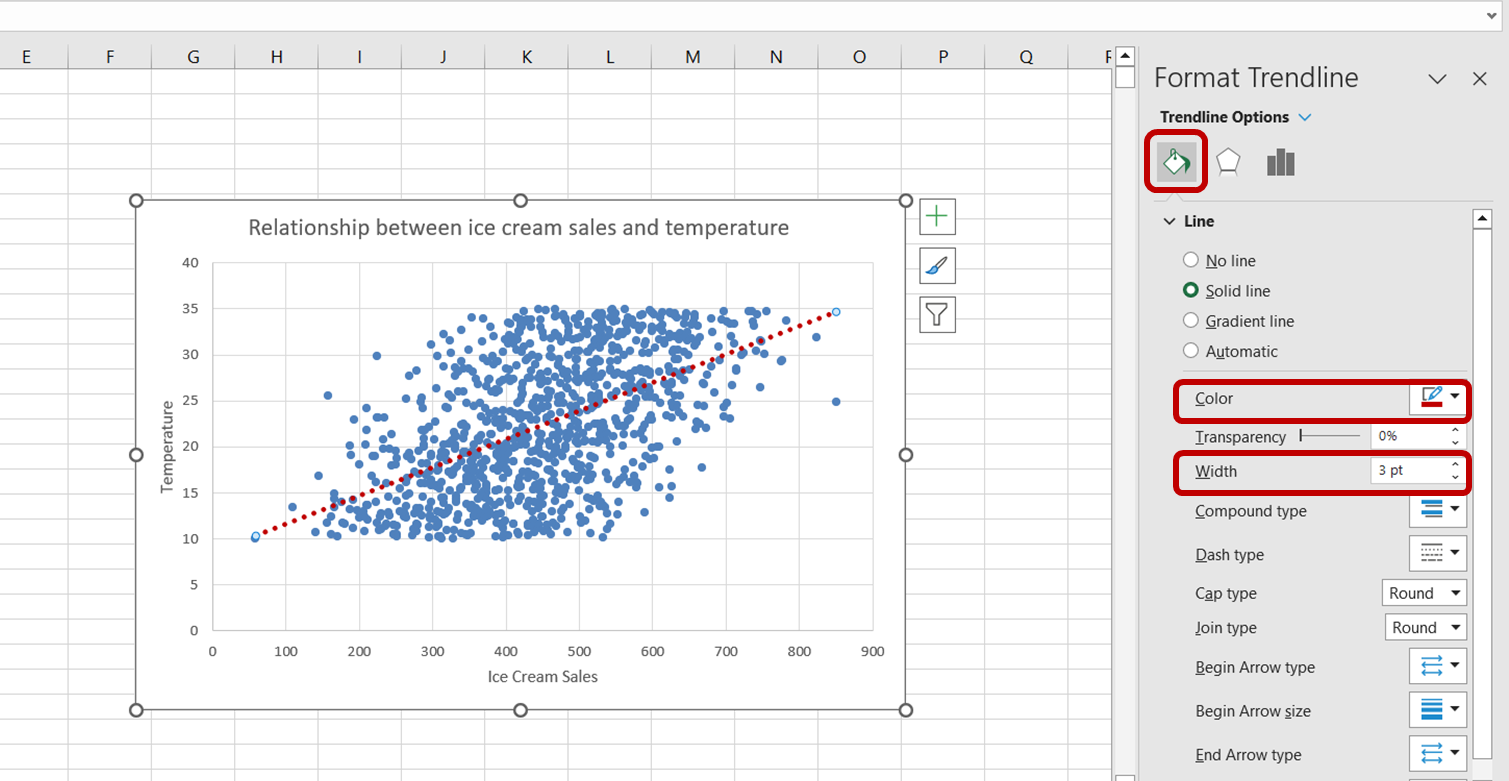
Nous avons maintenant réussi à créer une visualisation permettant de mieux comprendre la relation entre les ventes de glaces et la température.

Le graphique ci-dessus montre qu'il existe une relation positive entre la température et les ventes de glaces. Lorsque la température augmente, il semble que les ventes de glaces augmentent également, ce qui indique que la température est un facteur prédictif significatif des ventes de glaces.

Notez que cette observation est similaire à celle que nous avons tirée des résultats de l'analyse de régression dans la section précédente.

Réflexions finales

Vous avez maintenant acquis de solides connaissances sur la manière d'effectuer une régression linéaire dans Excel, d'interpréter diverses mesures statistiques pour évaluer l'adéquation d'un modèle et de visualiser l'analyse de régression à l'aide de diagrammes de dispersion et de courbes de tendance.

Mais le voyage ne s'arrête pas là.

Croyez-le ou non, nous n'avons fait qu'effleurer la surface de la modélisation prédictive, et il reste encore beaucoup à apprendre. Voici quelques pistes pour approfondir votre compréhension du sujet.

Pratique

Mettez en pratique les concepts que vous avez appris dans cet article afin de ne pas les oublier. Par exemple, prenez l'ensemble de données utilisé dans ce tutoriel et créez un diagramme de dispersion pour illustrer la relation entre les ventes et les prix des crèmes glacées.

Vous pouvez même aller plus loin en apprenant à afficher l'équation de régression sur la ligne de tendance.

Maîtrise d'Excel

Comme nous l'avons vu plus haut dans cet article, l'utilisation intensive d'Excel dans de nombreuses organisations en fait un outil très demandé. Une bonne maîtrise d'Excel peut améliorer considérablement vos chances de trouver un emploi dans divers secteurs d'activité, en raison de son application très répandue.

Si vous avez rencontré des difficultés en suivant ce tutoriel, ou si vous n'êtes pas encore à l'aise avec les formules d'Excel, envisagez de vous inscrire à notre cursus d'apprentissage Excel Fundamentals. Ce cours vous présentera diverses techniques de visualisation de données, des tableaux croisés dynamiques et des fonctions logiques telles que les COUNTIFs et les IFs imbriqués, ouvrant ainsi la voie à la maîtrise d'Excel.